無人機MEMS加速度計的混合誤差補償
吳鎮 宋宇

摘 要:針對慣性導航系統中三軸MEMS加速度計的零位偏移誤差、非正交誤差、靈敏度誤差等多種誤差,提出一種基于最大似然估計的混合誤差補償方法,建立三軸加速度計混合誤差模型。采集實際慣性傳導系統輸出數據作為樣本,通過梯度下降法進行迭代,以達到算法收斂。該算法對三軸加速度計的混合誤差進行隱式求解,其結果包括已知誤差與未知誤差,是一種包含加速度計全部誤差的補償算法。實驗對比誤差補償前后加速度計輸出在空間坐標系的分布和在姿態解算中的估算結果,實驗結果表明,該算法能對三軸加速度的混合誤差進行有效補償,是一種有效且易于實現的方法。
關鍵詞:慣性導航系統;加速度計;混合誤差;隱式求解;空間分布;誤差補償
0 引 言
慣性導航系統(Inertial Navigation System,INS)是無人機的基本組成部分,是無人機維持正常飛行的重要依賴。慣性導航系統多由多個不同類型的慣性傳感器件組成,通過多個傳感器返回不同數據進行數據融合,從而得到較為精確的姿態參數。加速度計是慣性導航系統中常見的組成部分。常用的MEMS加速度計由于制造工藝與傳感器安裝等條件限制,加速度計的數據輸出中含有固定存在或者周期性存在的噪聲,噪聲在后續的數據融合、姿態估算中參與計算,將會給后續計算帶來較大誤差,進而影響導航系統的正常工作。
因此,對未參與數據融合的加速度計的數據進行預處理,是一種目前常見的手段。國內外學者會根據不同需求,對加速度計存在的不同誤差進行針對性測量與修正,以達到工作目標。文獻[1-3]中,對加速度計進行重力法標定,適合對靜態靈敏度誤差和零位偏移誤差進行測量與標定。文獻[4-6]中采用極限學習機、BP神經網絡進行誤差修正,得出一組隱式補償參數,利用這組補償參數對加速度計輸出進行補償。文獻[7-8]中對振動狀態下加速度計的輸出數據進行分析,濾除振動條件下特有的高頻噪聲。文獻[9-10]中針對重力法中需要大型標定臺的缺陷,采用橢球擬合方法,進一步簡化了誤差測量對設備的需求。
本文將針對加速度計的零位偏移誤差、靈敏度誤差、非正交誤差以及軸間串擾進行誤差分析,并通過MEMS加速度計傳感器進行試驗,證明算法的有效性。試驗結果表明,該算法可以有效濾除加速度計中的誤差,大幅提高加速度計在飛行運動中的測量精度。
1 三軸加速度計誤差模型
1.1 三軸加速度計誤差分析
文獻[11-13]中描述了三軸MEMS加速度計的測量結果受生產技術與制作工藝的限制,產生的固有誤差主要包括零位偏移誤差、靈敏度誤差、非正交誤差以及軸間串擾。
零位偏移誤差受制作工藝的影響,無加速度輸入時,加速度計也會存在一定非零輸出,可以使用常量a0表示,a0∈R3。
靈敏度誤差產生的原因在于三軸模擬信號與數字輸出比例不完全一致,可以采用一個對角矩陣Sa=diag(Sax,Say,Saz)表示。
非正交誤差同樣由于工藝限制,因三軸不能實現完全正交而產生誤差。正交坐標p其坐標軸為Xp,Yp,Zp,加速度坐標軸為Xa,Ya,Za,兩者原點重合,且Xp與Xa重合,如圖1所示。
三軸加速度計的軸間串擾原因在于各軸輸出間相互影響,可采用一組常數表示。
1.2 三軸加速度計誤差參數模型
假定三軸加速度計噪聲不隨傳感器姿態變化,結合上述可以獲得三軸加速度計誤差模型:
式中:ak為加速度計讀數;矩陣S為靈敏度誤差與非正交誤差;矩陣C為非正交誤差矩陣;atrue, k為加速度計的真實值;a0為加速度計的零位偏移誤差;na為加速度計的隨機誤差。
2 橢球擬合算法的誤差補償
文獻[14-15]中所述,傳統加速度計重力標定方法存在對設備要求高、標定成本高,在普通無人機慣性導航系統上難以應用等問題,本文采用橢球擬合算法對三軸加速度計數據進行補償。利用加速度計靜止時只承受重力作用的特點,使加速度計處于靜止但非特定姿態下進行測量。該方法無需借助昂貴的外部設備,通過大量采集不同姿態下的數據進行測定,同樣具有較高的精度。
2.1 橢球擬合算法原理
在理想狀態下,加速度計處于靜止狀態時只受重力作用,對各軸的測量值進行合成后將得出一個方向向地心,大小為g的加速度。因此,理想狀態下不同姿態下的加速度計輸出在空間坐標系上的分布將呈現為一個半徑為g,球心與坐標系圓點重合的球形。非理想狀態下,在加速度計的誤差噪聲影響下,加速度計輸出數據在空間坐標系上的分布將不再是一個完全的球形,與此同時,對加速度計誤差模型產生的超定方程使用最大似然估計法進行橢球擬合,求解得到包括隨機誤差在內的隱式誤差參數,利用該參數對加速度計誤差進行混合補償。
2.2 最大似然估計的橢球擬合算法
本文利用最大似然法求解三軸加速度計誤差參數。
2.3 最大似然估計原理
最大似然估計函數在采樣的樣本總數區域無窮時能達到最小方差,本文利用FPGA作為通信控制手段,自MEMS傳感器模塊中采集大量樣本數據,以實現方差最小化。假定加速度計噪聲是一種服從正態分布,方差為σ2a,k,均值為零的高斯過程,則可知加速度計的測量值同樣服從高斯分布:
當滿足條件||xk-xk-1||≤ε時,迭代完成,算法收斂,此時的xk為較為理想的估計值。式(9)的迭代需要對初始參數進行設定,本文采用最小二乘法對參數進行預擬合,獲取初始參數x0。
3 結果與分析
本文采用三軸加速度傳感器輸出作為樣本,以FPGA作為對傳感器進行數據采集并與PC端通信的中樞。通過PC端在MATLAB中對三軸加速度計利用上述算法進行誤差估計,對比修正前后的數據在空間坐標系下的分布,并將誤差數據導入實際慣性導航系統中,對比加速度計輸出數據修正前后對姿態解算的影響。
目前常見的三軸MEMS加速度計都具有輸出修正功能,即通過人為設置零位偏移誤差數值,對三軸加速度計的輸出進行預處理。本文中的三軸加速度計傳感器中預設零位偏移誤差值均為零,以保證三軸加速度計數據的原始性。
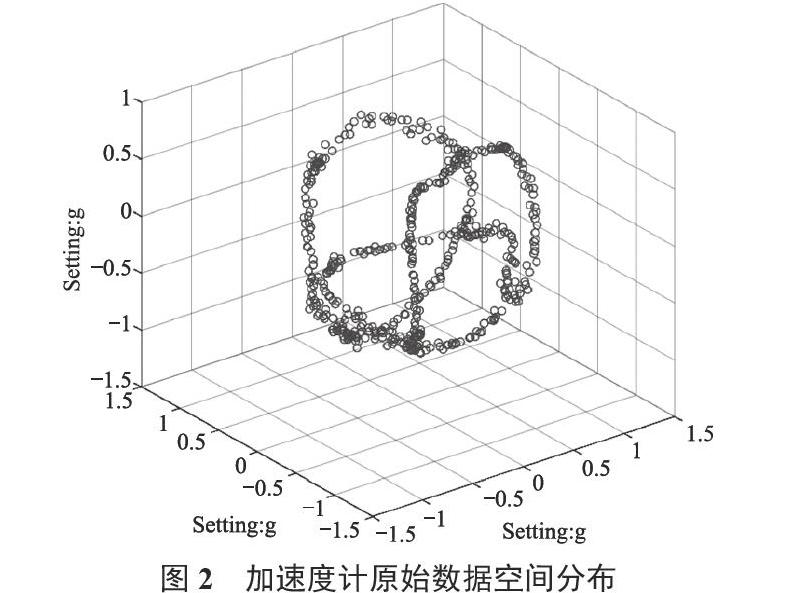
為了獲取迭代數據的初始值,先采集三軸加速度計不同靜止姿態下的數據,選取其中20組數據,采用最小二乘法擬合數據,獲取初始參數x0。其三軸加速度計的原始輸出在空間坐標系下的分布如圖2所示。
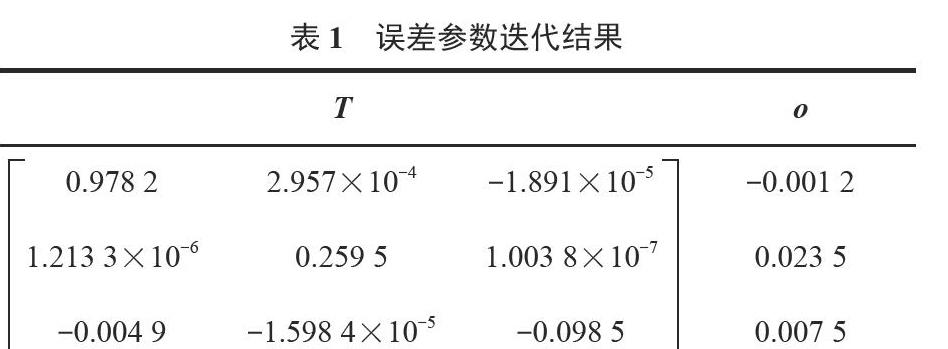
將x0作為初始參數,重新采集數據作為樣本數據,取慣性導航系統在同一姿態下靜止5 s時數據的平均值作為一份樣本,采集200組數據樣本。在式(9)中進行迭代,結果見表1所列。
將修正后的結果導入比力方程中進行位移誤差實驗。理想狀態下根據比力方程計算加速度的二次積分結果應為零,具體見表2所列。
4 結 語
本文采用橢球擬合法對三軸加速度計誤差進行標定,解決常見重力法標定帶來的成本高與條件苛刻等問題,并采用最大似然估計法對誤差參數進行隱式求解。有別于傳統最小二乘法對指定目標誤差參數求解時需假定未指定誤差參數為零的做法,采用最大似然估計法對三軸加速度計混合誤差進行誤差參數求解,其結果能隱式表示三軸加速度計中已知與未知的誤差。實驗結果表明,本文采用的加速度計誤差補償方法有效、方便。
參考文獻
[1] Yu Mingbiao,Cai Tijing.Erratum:"Calibration of a rotating accelerometer gravity gradiometer using centrifugal gradients"[J].The review of scientific instruments,2018,89(10).
[2] RANJBARAN S,EBADOLLAHI S. Fast and precise solving of non-linear optimisation problem for field calibration of triaxial accelerometer[J].Electronics letters,2018,54(3):148-150.
[3]劉宇,余躍,路永樂,等.MEMS加速度計混合誤差標定補償方案[J].壓電與聲光,2018,40(4):589-593.
[4] Xu H E,Zhen Hai Z,Ke Jie L I,et al. Triaxial high-g accelerometer of microelectro mechanical systems[J].北京理工大學學報(英文版),2015(4):427-431.
[5]杭義軍.多旋翼無人機微導航系統誤差補償與信息融合技術研究[D].南京:南京航空航天大學,2017.
[6]石崗.慣性與磁傳感器組合航向估計方法研究[D].北京:北京科技大學,2019.
[7]高暢.基于MEMS的IMU誤差建模與溫度補償技術研究[D].哈爾濱:哈爾濱工程大學,2017.
[8]劉艷霞,方建軍,石崗.基于改進極限學習機的三軸加速度計誤差補償算法[J].傳感器與微系統,2019,38(7):138-141.
[9]王向軍,張朝陽,劉峰.基于加速度分離算法的姿態測量方法研究[J].傳感技術學報,2018,31(12):1848-1892.
[10]高爽,張若愚.基于自適應遺傳算法的MEMS加速度計快速標定方法[J].北京航空航天大學學報,2019,45(10):1982-1989.
[11]黃欽文,楊少華,董顯山,等.加速度計標定中靜態半徑誤差項的消除技術[J].中國慣性技術學報,2018,26(1):122-126.
[12]崔智軍.微型捷聯航姿系統誤差分析與補償[J].儀表技術與傳感器,2018(8):98-102.
[13]魯瀚杰,劉亞斌,周強.一種基于慣導系統的線加速度計動態性能測試方法[J].兵器裝備工程學報,2019,40(12):165-170.
[14]占偉偉,蔡莉.一種減小加速度計重力法標定中安裝誤差影響的方法[J].振動與沖擊,2019,38(13):249-252.
[15]于沛,閆祿,張金云,等.振動條件下陀螺加速度計誤差抑制技術[J].噪聲與振動控制,2019,39(2):37-41.
[16]李久順.捷聯慣導系統誤差抑制及補償方法研究[D].哈爾濱:哈爾濱工程大學,2018.

