一種全局搜索策略的鯨魚優化算法

劉 磊，白克強，但志宏，張 松，劉知貴，3

1(西南科技大學 信息工程學院，四川 綿陽 621000)2(中國航發四川燃氣渦輪研究院，四川 綿陽 621703)3(西南科技大學 計算機科學與技術學院，四川 綿陽 621000)

E-mail：liuzhigui@swust.edu.cn

1 引 言

鯨魚優化算法(whale optimization algorithm，WOA)是2016年由Seyedali Mirjalili 教授[1]提出的一種群智能優化算法，通過模仿鯨魚在海洋中捕捉食物的搜尋過程，來尋找最優解.該算法具有結構簡單、自身參數少的特點，在多元函數求解方面比傳統粒子群優化算法[2]和遺傳算法[3]的速度更快、精度更高.在實際工程中的應用也開始增多，Khaled等[4]使用WOA對電力系統的調度進行優化，實現了對無功功率的最優調度.Yu等[5]將WOA應用在控制器的參數整定中，優化后的參數可以使控制系統具有更強的魯棒性.但是WOA也存在傳統群體優化算法的弊端，全局搜索能力不足，算法尋優精度低等問題.

為了解決傳統鯨魚優化算法的缺陷，Oliva等[6]提出一種混沌鯨魚優化算法，使用混沌策略指導鯨魚位置更新，一定程度避免了陷入局部最優解.牛培峰等[7]將反向學習策略運用到鯨魚位置初始化中，提升了算法的搜尋效率.目前已有大量改進的WOA算法提出，但大多的改進都沒考慮到螺旋更新方式對算法尋優的影響，以及算法在全局搜索能力上的不足.

針對上述問題，本文提出一種全局搜尋策略的鯨魚優化算法(global search whale optimization algorithm，GS-WOA).該算法采用變螺旋更新方式，增加鯨魚尋優過程中的螺旋路徑選擇；使用自適應權重改變鯨魚位置更新時的速度，動態調整權值來提升算法后期的收斂速度；通過最優鄰域擾動的策略，來避免算法的早熟現象.為檢驗GS-WOA的尋優性能，在多個測試函數上進行仿真實驗，結果表明了該算法具有更高的尋優精度和更快的收斂速度.

2 鯨魚優化算法

鯨魚自身體積比較龐大，在海里移動相對來說不是特別靈活，想要捕獲更多的小魚就需要一種獨特的群體合作的方式，找到最多小魚群的位置.鯨魚的群體捕捉過程如圖1所示，鯨魚通過向上螺旋靠近目標，并逐漸縮小包圍圈，最終到達目標魚群的位置.根據捕食特點，WOA包括三種位置更新方式：包圍獵物、旋轉搜尋以及隨機搜尋.

圖1 捕獵示意圖Fig.1 Hunting diagram

2.1 包圍獵物

鯨魚將目前搜尋到的獵物信息共享，然后鯨魚向當前群體中最接近獵物的那頭鯨魚靠近，逐漸收縮整個鯨魚群的包圍圈，實現對獵物的包圍.該環節鯨魚位置更新公式為：

(1)

式中：t為迭代搜尋次數；X為鯨魚位置；X*是全局最優位置；A和C為系數矩陣，表達式為：

(2)

式中：r1和r2是[0，1]均勻分布隨機數；t為迭代次數；tmax為最大迭代次數；a為收斂因子，從2到0線性遞減.

2.2 旋轉搜尋

鯨魚搜尋獵物是螺旋向上，慢慢靠近目標的方式，螺旋搜尋的表達式為：

(3)

式中：b為常數，可以改變螺旋的形狀；l為[-1，1]均勻分布隨機數.

鯨魚在螺旋搜尋獵物的時候，還會收縮包圍圈，所以為了模擬這種行為，需要包圍獵物和螺旋搜尋同步進行.更新公式為：

(4)

式中：p為[0，1]之間均分布隨機數.

2.3 隨機搜尋

為了提升鯨魚的全局搜索能力，讓鯨魚在搜尋獵物時具有一定的隨機性，增加鯨魚群的搜尋范圍.

當系數|A|≥1時，說明該鯨魚在收縮包圍圈外，選擇隨機搜尋方式；當系數|A|<1時，說明該鯨魚在收縮包圍圈內，選擇螺旋包圍搜尋方式.隨機搜尋更新公式為：

X(t+1)=Xrand(t)-A·|C·Xrand(t)-X(t)|

(5)

式中：Xrand為一個隨機的鯨魚位置.

以上三種搜索方式的結合構成鯨魚優化算法.

3 改進的鯨魚優化算法

通過分析發現，鯨魚優化算法在收斂速度和全局搜索能力上還存在一定缺陷.根據標準鯨魚位置更新方式，引入三種改進方式構成全局搜索策略提升算法的尋優能力.

3.1 自適應權重

受粒子群優化算法的啟發，在鯨魚的位置更新中加入一個隨迭代次數變化的慣性權重w.在算法搜索的前期，削弱最優鯨魚位置對當前個體位置調整的影響，提升算法在前期的全局搜索能力.隨著迭代次數的增加，逐漸提升最優鯨魚位置的影響力，使得其他鯨魚能夠快速收斂到最優鯨魚的位置，提升整個算法的收斂速度.根據鯨魚優化算法中更新次數的變化，選用迭代次數t構成的自適應慣性權值如下：

(6)

這樣的慣性權值w具有一種在[0，1]之間非線性變化的屬性，由于cos函數在[0，π/2]之間的變化特性，使得權值在算法初期較小，但變化速度稍快；在算法后期其值較大，但變化速度會減緩，這樣可以充分保證算法收斂性.改進后的鯨魚優化算法位置更新公式為：

(7)

X(t+1)=w(t)Xrand(t)-A·|C·Xrand(t)-X(t)|

(8)

在引入自適應權重之后的位置更新，會根據迭代次數的增加，動態調節權重大小，使得最優鯨魚位置X*(t)在不同時刻對鯨魚個體的指導不同.隨迭代次數的增加，鯨魚群的會集中向最優位置方向靠近，并且此時權值較大會使鯨魚位置移動速度加快，進而加快算法收斂速度.

3.2 變螺旋位置更新

鯨魚在搜尋獵物的時候，會根據目標位置與自身位置之

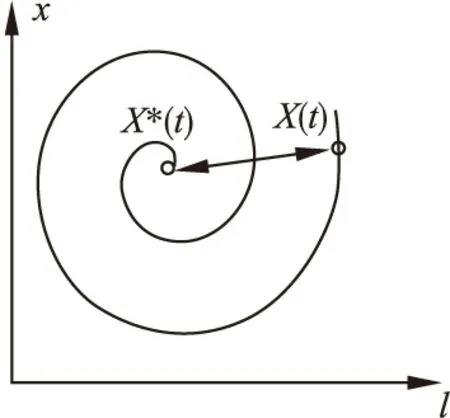
圖2 螺旋更新位置Fig.2 Spiral update position

間的螺旋形狀，調整每次位置更新的移動距離，如圖2所示.在螺旋搜尋模型式(3)中，b是控制螺旋形狀的常數，該參數一般設置為常數，每次位置更新按照不同的螺旋弧度進行速度調節.但是b設置為常值會導致鯨魚在搜尋獵物時的螺旋移動方式過于單一，每次都是按照固定的螺旋線靠近目標，極易陷入局部最優解的誤區，削弱算法全局搜尋能力.

針對該問題，為了使鯨魚能夠開發更多樣的搜索路徑進行位置更新，引入變螺旋搜尋的思想，將參數b設計為隨迭代次數改變的變量，動態調整鯨魚搜尋時的螺旋形狀，增加鯨魚對未知區域的探索能力，進而提升算法全局搜索能力.結合自適應權值后，新的螺旋位置更新公式如下：

(9)

參數b是根據螺旋線的數學模型進行設計的，在原有螺旋線模型的基礎上，通過引入迭代次數，動態調整螺旋形狀.這樣設計的參數b會隨迭代次數增加，使螺旋形狀從大到小的變化.在算法前期鯨魚以較大的螺旋形狀搜尋目標，鯨魚盡可能多的去探索全局最優解，提升算法的全局最優搜尋能力；在算法后期鯨魚以小螺旋形狀搜尋目標，提升算法的尋優精度.

3.3 最優鄰域擾動

鯨魚在更新位置的時候，一般都是以當前最優位置作為本次迭代的目標.在整個迭代環節中，最優位置只有在出現優于它的位置時才會更新，所以總的更新次數不多，導致算法搜尋效率不高.針對此，引入最優鄰域擾動策略，將最優位置的附近隨機搜索一遍，找到一個更佳的全局值，這樣不僅可以提升算法的收斂速度，而且還能避免算法出現早熟.

最優位置產生隨機擾動，增加其對附近空間的搜索，鄰域擾動公式為：

(10)

對于生成的鄰域位置，采用貪婪的策略判斷是否保留，公式如下：

(11)

式中：f(x)為x的位置適應值.如果生成的位置比原位置好，則將其與原位置替換，使其成為全局最優.反之，最優位置保持不變.

3.4 算法流程

改進鯨魚優化算法的流程如表1所示.

3.5 算法復雜度分析

時間復雜度可以作為評判一個算法運算量的重要手段.在鯨魚優化算法中，設算法中鯨魚的規模為N，最大迭代次數為T，問題維度為D.可以得到WOA的時間復雜度為O(N*T*D).而GS-WOA在原有算法的基礎上引入三種改進策略，從該算法流程可以看出，在加入自適應權重和變螺旋更新策略未增加循環次數，算法時間復雜度為O(N*T*D)，而加入最優鄰域擾動給算法外圍增加了一次遍歷種群的循環，增加了O(N*T)的運算量.對于整個算法的時間復雜度來說，增加O(N*T)的運算量不會對算法造成太大計算負擔，總體來說GS-WOA的時間復雜度與標準WOA時間復雜度持平.

表1 算法流程Table 1 Algorithm flow

空間復雜度用來評判一個算法對內存空間的需求情況.在這里空間復雜度主要由鯨魚的規模和所需求解問題的維數決定，GS-WOA和WOA具有相同的空間復雜度O(N*D).

4 算法性能測試

4.1 測試函數及性能指標

為了測試GS-WOA算法的尋優能力，在文獻[1]中選擇了11個基準函數.其函數特性如表2所示.算法尋優精度為實際尋得最優解與理論最優解之間的誤差絕對值，本文采用兩個評價指標：尋優精度的平均值(Ave)和標準差(Std).其計算公式如下：

(12)

式中：Xopt為理論最優解；N為總的實驗次數.

4.2 優化算法的性能分析

使用GS-WOA算法在11個基準函數上進行測試.維數Dim分為30和200，并將其與GWO[8]、WOA和SM-WOA[9]算法進行比較，對比4種算法的性能指標.4種算法的參數設置相同：規模N為30；最大迭代次數為500.4種算法均單獨測試30次，得到優化結果的平均精度及其標準差如表3所示，其中黑色粗體為較優結果.

表2 基準測試函數Table 2 Benchmark function

表3 尋優指標對比Table 3 Comparison of optimization indexes

從表3中可知，GWO算法的尋優精度普遍較低，只有在測試函數f3、f4上優于WOA算法.SM-WOA算法在尋優精度上面有所提升，但缺乏全局搜索能力，在函數f5、f6和f11上，算法的尋得的最優解和理論值有一定偏差.GS-WOA算法在這些測試函數上的尋優精度都優于其余對比算法，并且標準差相對較低，表明算法較為穩定，其中對函數f1、f3、f8、f10的求解，可以搜尋到理論最優值.當問題維數上升后，所有優化算法的尋優精度都有所降低，但GS-WOA算法仍然保持了較高的尋優精度和穩定性.

圖3為WOA、MS-WOA、GWO和GS-WOA算法在基準測試函數上求解的收斂曲線對比圖.

從圖3中可以看出，GS-WOA算法的收斂速度普遍要比其余3種算法快，并且尋優精度更高.由圖中(e)、(f)、(g)和(k)可以知，在函數f5、f6、f7和f11上，GWO、WOA和MS-WOA都陷入的局部最優解，而GS-WOA由于變螺旋更新方式提升了算法全局搜索能力，使得算法可以突破局部最優的限制尋找到新的全局最優解.總體來說，GS-WOA算法具有更高的尋優精度和求解能力.

圖3 收斂曲線對比圖Fig.3 Convergence curve comparison diagram

為了驗證GS-WOA改進策略的有效性，將其與CWOA[10]、W-SA-WOA[11]和IWOA[12]進行對比，基準測試函數任選擇之前的11個，鯨魚規模為30，最大迭代為500次，獨立運行30次實驗，并引用文獻[10-12]中的一些數據，對比分析各算法性能指標，結果如表4所示(“-”表示參考算法未做該項實驗)，較優結果已用粗體標出.

表4 與其他改進算法的對比Table 4 Comparison with other improved algorithms

由表4可知，在已給出的測試函數上，GS-WOA的尋優精度優于CWOA、W-SA-WOA和IWOA三種算法，并且具有較高的穩定性.

綜上所述，GS-WOA在求解復雜函數的最優解時，比傳統WOA的求解精度高很多，與目前改進的WOA算法相比，GS-WOA能找到更好的全局最優解.

5 總 結

鯨魚優化算法是一種具有仿生尋優的智能優化算法，但是在處理復雜函數優化問題時仍存在一些局限性.本文分析了標準WOA的尋優過程，根據目前位置更新存在的問題，提出了相應的解決方法.為了防止WOA算法易陷入局部最優解，加入自適應權值、變螺旋更新和最優鄰域擾動策略，調整鯨魚位置更新的方式，動態調節鯨魚向目標物靠近的速度，進而提升整個算法的全局搜索能力.通過在基準函數上的測試，結果表明了GS-WOA算法能夠突破局部最優解的限制，獲得更高的求解精度.相比于其他改進算法，GS-WOA具備更強的全局搜尋能力，證明了本文針對WOA提出的三種改進策略的有效性.