基于隨機圖的復雜網絡建模方法研究
李 姝,邵志香,于金剛
1(沈陽理工大學 裝備工程學院,沈陽 110159)2(頁巖油氣富集機理與有效開發國家重點實驗室,北京 100101)3(中國石化石油工程技術研究院,北京 100101)4(中國科學院 沈陽計算技術研究所,沈陽 110168)
E-mail:lishucx@163.com
1 引 言
近年來,復雜網絡系統的研究在不同領域發揮著越來越重要的作用.隨著計算機與互聯網技術的蓬勃發展,建立一個滿足接近于真實互聯網通信需求及最短通信鏈路的復雜網絡模型,以此為基礎進行復雜網絡的研究是十分有意義的.由于復雜網絡分布錯綜復雜,且網絡傳輸中受網絡承載量及傳輸質量等諸多因素的限制,雖然表面上復雜網絡的傳輸路徑是隨機的,但這并不意味著復雜網絡毫無規律可循.有研究表明,很多網絡具有小世界性質[1,2],即從原點節點到目的節點的訪問路徑存在一條“相對固定”的最短通信鏈路.這里的“相對固定”是根據一定的發生概率而言的,即從源節點到目的節點的通信鏈路是存在一定的訪問概率的,這說明人們訪問某個站點或者服務器的通信鏈路也是相對固定的[3,4].
根據上述研究,有研究者提出利用隨機圖理論可以生成與真實網絡訪問拓撲結構具有高相似度的隨機圖網絡模型,能夠更好的模擬與研究復雜網絡的通信[5,6].基于此,本文在隨機圖理論的基礎上,提出了基于隨機圖的樹型網絡仿真模型k-RGN,該網絡模型是一種充分考慮連接鏈路權重,且服從指數分布的隨機網絡模型.通過網絡模型的對比實驗,驗證了k-RGN隨機網絡模型在帶寬、丟包率、時延、時延抖動、跳數等多參數指標規劃中,具有最優的網絡性能.
2 隨機圖理論與隨機圖模型
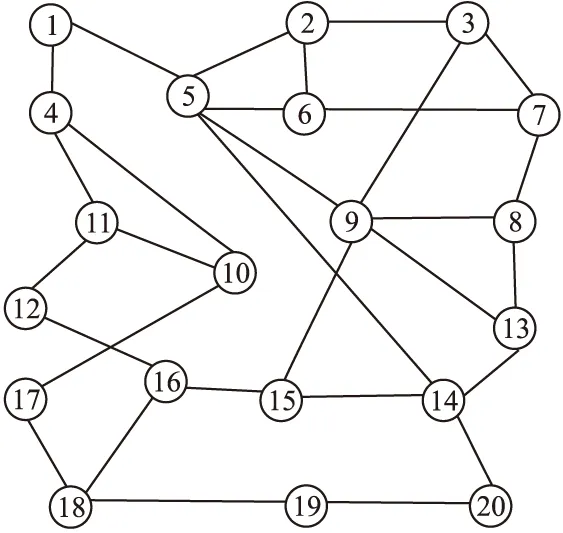
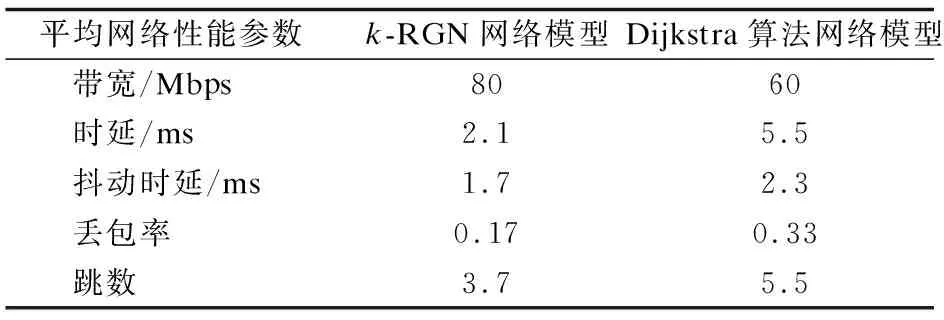
設某個概率空間中的每一節點都看作是一個圖,則稱這些圖為隨機圖[7,8].其中隨機圖Gp(n)定義:概率空間由V={1,2,…,n}為節點的n個圖集組成.其中n個節點是可區別的,即每個圖被認為是不同的圖,出現概率p滿足0 隨機圖Gp(n)最廣泛的應用之一是建立隨機網絡,研究者們一直以來致力于研究出一種被廣泛用來生成復雜網絡的隨機圖模型方法,達到生成具有指定度序列[9]或者具有指定冪律分布的復雜網絡.用隨機圖生成隨機網絡模型,其建模方法如下[10,11]: 給隨機圖Gp(n)中的每個節點都附加一個頂點權重w,則節點i與節點j之間存在一條邊的概率為: (1) 將頂點賦予權重,可以使得隨機圖模型更好的適應于網絡的實際分布.節點的權重越大,表明該節點與其他節點相連的概率就越大,我們通過選取合適的節點權重,來構建一個更貼近于實際網絡的隨機模型.假設我們構造了一個包含兩種不同類型節點的網絡,第一類節點的權重為w1,第二類節點的權重記作w2,n1與n2分別表示第一類節點與第二類節點的個數.即: ln=n1w1+n2w2 (2) (3) 由式(3)可知,第一類型節點的期望度數趨近于w1.同理可推,第二類節點的期望度數趨近于w2. 由上可知,基于隨機圖的網絡結構高度依賴于頂點權重,在實際網絡中,頂點的權重可以設置固定值,或更加復雜的隨機變量序列.為了研究頂點權重的經驗性質,我們定義頂點權重的經驗分布函數: (4) 可以將Fn(x)看成隨機選取節點權重的分布函數,在應用中,通常假設頂點權重服從正則化條件. 根據隨機圖理論在隨機網絡中的建模可知,雖然隨機網絡模型與物理上的網絡拓撲結構并不一致,但它與實際的網絡訪問結構或者路由連接鏈路可以有很好的吻合.然而,隨著隨機圖理論應用于通信網絡建模的研究深入,有研究表明[12-14],廣義隨機網絡模型只適合于普通簡單規模的網絡訪問模型,對于大型復雜通信網絡,其網絡模型表現并不理想. 鑒于此,本文在隨機圖理論的基礎上,提出一種基于隨機圖的k-叉樹網絡模型(k-RGN),使得隨機圖Gp(n)的網絡模型服從于指數分布,進而適用于大型復雜通信網絡結構;此外,k-RGN網絡模型充分考慮連接鏈路的權重問題,使隨機網絡模型更適用于實際網絡訪問需求和最短訪問路徑的復雜網絡. 設一棵k叉樹由一個源點和N個節點組成,樹深度D等于從源點到節點的跳數,m為隨機選取的遍歷節點個數,k為樹的分枝數,k叉樹網絡模型如圖1所示.在一棵k叉樹中,節點的總數滿足下式: (5) 由公式(5)可知,N服從于kD,記N~kD. 我的爸爸還是一個幽默搞笑的人。有一次,他無意間撈到了一只青蛙,“看!這只青……”他剛說到這里,那只青蛙就回頭看了看他,“撲通”一聲跳進了水里,弄得他滿臉都是泥水,就像是一只“大青蛙”。我看了一眼被泥水濺成“大花臉”的爸爸,“撲哧”一聲笑了出來。 圖1 k-叉樹網絡模型k=2,N=21,D=4Fig.1 k-tree network model k=2,N=21,D=4 建立k-RGN網絡模型,需要考慮兩點問題:1)隨機圖網絡的連通性,即隨機生成樹應遍歷所有節點,并且確保每個節點都是雙連通的;2)隨機鏈路的產生,即我們如何讓產生的隨機網絡更接近于真實網絡的連接狀況.具體步驟如下: 1)產生隨機節點.首先建立笛卡爾坐標系xoy,將坐標系以整數最小單位劃分成網格(可以將網格單位設為1),利用整數隨機發生器產生隨機節點,使隨機節點均落在網絡上;然后分別檢查產生節點的橫縱坐標間距,刪除掉間距小于5的隨機節點,并重新生成節點,直至滿足間距為止; 2)產生隨機鏈路.網絡的隨機節點產生后,接下來在這些節點中建立隨機鏈路,這里的“隨機鏈路”并非是完全的隨機,這里我們模擬與實際網絡訪問鏈路最接近的連接方式,構建一個連通的隨機網絡. 在實際的網絡通信中,通常是節點間距離越大,節點間建立連接的可能性越小,但我們并不能簡單地以距離作為節點間連接的依據,這與實際需求中的網絡通訊結構并非一致.本文基于隨機圖理論,將節點間的距離設為連接權重,并帶入節點間存在鏈路的概率P中.連接概率P與節點間的距離有關,建立節點間連接概率P函數如下: (6) P(u,v)是節點u和節點v之間存在連接的概率,d(u,v)是它們之間的距離,L是網絡節點間可能的最大距離之和,權重參數w是控制遠程連接和本地連接所占的比重,長連接的比重越大,w取值越大.值得說明,參數w應該服從公式(4)經驗分布函數Fn(x),這里為方便計算,我們設w取值為0到1.參數γ調節網絡的平均節點度數,γ越大,網絡平均節點度數越多. 3)檢查網絡連通性.使用式(6)產生的隨機網絡在大量節點時,不能保證網絡的連通性.為了糾正網絡的非連通性,我們再檢查網絡中的每個節點的連接度數,如節點的連接度數為1時,將該節點與網絡中的其他節點隨機產生一條鏈路.經過反復處理,產生的隨機網絡一定是有雙連接的連通網絡. 圖2 k-RGN網絡模型Gp(20)Fig.2 k-RGN network model Gp(20) 實驗選取200*200的笛卡爾坐標,橫、縱坐標的隨機數在0到200之間產生,坐標軸最小刻度單位為1.設隨機網絡的節點個數N=20,權重參數w=0.16,調節系數γ=3.7.實驗任意選取節點u和節點v,根據公式(6)計算它們之間可能存在連接的概率P(u,v),在0到Rmax之間產生一個均勻分布的隨機數Ri,如果隨機數Ri的概率Pi滿足于公式(7),則節點u和節點v之間存在連接,否則不存在連接.反復隨機選取各節點,產生隨機連接.每當增加一條連接時,需要進行判斷是否達到了平均節點度數,若己經達到,則停止.如圖2所示選取節點數為20個時,產生的隨機網絡模型. Pi=Ri/Rmax (7) 本文基于隨機圖原理,建立了k-RGN網絡仿真模型,其研究意義在于預測k-RGN網絡仿真模型在實際通信的復雜網絡中所表現的連接狀況及網絡性能,為拓展復雜網絡理論研究和驗證實際應用效果提供依據.通常用以描述網絡綜合性能的指標包括:帶寬、時延、時延抖動、丟包率和跳數等. 時延是指一個報文或分組從一個網絡的一端傳到另一端所需要的時間,時延等于發送時延,處理時延,傳播時延與排隊時延之和.這里我們只計算傳播時延,即從一個節點進入下一節點所需的時間間隔.設tij是i節點到j節點之間的時延. 時延抖動是指信息通過節點的最大與最小時間延遲差.設sij是i節點到j節點之間的時延抖動. 丟包率是指在鏈路的傳輸過程中所丟失的包數與傳輸包的總數之比,它體現鏈路的可靠性.設lij是i節點到j節點之間的丟包率. 跳數是指路徑所經過的鏈路數(即從原點到目的節點所經過的節點數).設hij是i節點到第j節點之間的跳數. 在k-RGN網絡模型中,從節點i到節點j假設存在k條鏈路,則從節點i到節點j的總帶寬為: (8) 從節點i到節點j的總時延為: (9) 從節點i到節點j的總時延抖動為: (10) 從節點i到節點j的總丟包率為: (11) 從節點i到節點j的總跳數率為: (12) 實驗在最短路徑算法(Dijkstra算法)生成的網絡模型,與基于隨機圖的k-RGN網絡模型中進行,比較這兩種網絡模型的網絡性能.實驗分別選取,節點數n=20,60,100.對選取的各個節點數所限定產生的網絡規模分別為3*n個網絡連接單元.實驗分別選取0.1*n組,0.2*n組,0.3*n組隨機節點進行通信仿真,每組網絡獨立重復試驗20次,最后求取各參數均值.選取節點個數100時,網絡性能參數對比如表1所示. 表1 節點數100兩種模型的網絡性能參數對比Table 1 Comparison of network performance parametersat 100 nodes 通過對比試驗可知,在實驗選取節點個數為100個時,基于隨機圖的k-RGN的網絡仿真模型的網絡平均帶寬、時延、抖動時延、丟包率、跳數等性能參數均優于由Dijkstra算法生成的網絡模型.實驗結果說明,基于隨機圖的k-RGN的網絡仿真模型在多個網絡通信節點數的復雜網絡中,仍然表現出較好的網絡綜合性能. 本文在隨機圖理論的基礎上,結合k-叉樹模型提出了基于隨機圖的樹型網絡仿真模型k-RGN.該網絡模型是通過引入連接權重w,將復雜網絡模型更接近于實際網絡訪問的通信鏈路;此外k-RGN網絡仿真模型是服從指數分布的隨機網絡模型,其網絡節點度值符合平均值為np的泊松分布,且存在最短的連接鏈路d.最后通過模型的對比實驗分析,驗證了k-RGN隨機網絡模型在平均帶寬、丟包率、時延、時延抖動、跳數等多參數指標規劃中,均優于普通路由算法建立的網絡模型.基于隨機圖k-RGN網絡模型具有很好的網絡綜合性能,適用于復雜網絡建模.
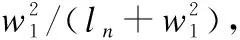
3 基于隨機圖的k-叉樹網絡模型

4 隨機圖k-RGN網絡模型的網絡性能分析
5 結 論

