利用一致性分析的高維類別不平衡數據特征選擇

曾海亮，林耀進，王晨曦，陳祥焰

(閩南師范大學 計算機學院，福建 漳州 363000) (數據科學與智能應用福建省高等學校重點實驗室，福建 漳州 363000)

E-mail：zzlinyaojin@163.com

1 引 言

在文本分類[1]、圖像識別[2]、醫學診斷[3]等研究領域，數據呈現出高維小樣本特點，即特征空間顯示高維性，而樣本數量過少.此外，該類數據通常伴隨著類別不平衡問題，如某一類的樣本數量遠大于另一類的樣本數量，易引發分類學習過程中大類樣本覆蓋小類樣本現象，而實際中小類樣本往往是關鍵的樣本[4].例如，信用記錄欺詐用戶的數量明顯低于正常用戶；常規體檢中重疾患者占極小比例.因此，如何提高高維類別不平衡數據中小類樣本的分類學習精度具有重要意義.

眾所周知，在高維類別不平衡數據分類建模任務中存在著小類樣本難以正確分類問題.為了提高小類樣本的預測精度，研究人員提出了眾多的類不平衡特征選擇算法[5-8].文獻[5]通過組合預先分別選擇的正特征和負特征，以期改善文本分類中類不平衡數據的分類性能.文獻[6]使用五種微陣列表達數據集對九種過濾技術進行了系統比較與分析，研究了抽樣技術在特征選擇中的應用，發現特征選擇有利于處理類不平衡數據.文獻[7]通過重構鄰域粗糙集下近似算子，提出了基于特征和標記之間依賴關系的在線特征選擇框架，旨在處理流特征環境下的類不平衡問題.文獻[8]運用了基于小類依賴度的在線流式特征選擇模型，并改進了鄰域粗糙集的依賴度計算公式.

在高維類別不平衡數據多分類學習任務中，若數據中類別分布傾斜得十分明顯時，特征選擇技術可以將所有樣本都分到大類從而獲得很高的分類精度.然而，卻忽略了至關重要的小類樣本，失去了實際意義.另外，有些特征選擇方法[9]將數據集某一類設置成小類樣本，其余類別樣本設置成大類樣本，這種人為設置大小類具有一定主觀性，很難體現數據的多樣性與復雜性.

從認知角度出發，樣本在論域空間的分布隨特征的變化而變化，具有高可分離性的特征應使樣本類內分散度盡量小，類間分散度盡量大.基于此，選擇好的特征能顯著提高高維類別不平衡數據的分類性能.基于最近鄰思想，相同特征空間下越相近的樣本其類別往往比較一致.于是，本文通過定義樣本一致性概念來構建高維類別不平衡數據特征選擇模型.首先，通過樣本在特征與類別標記的信息定義樣本的近鄰，并設計面向高維類別不平衡數據的一致性分析模型；其次，根據特征重要度公式構造前向貪婪搜索算法進行特征選擇；最后，通過實驗表明該模型的有效性.

綜上，本文內容安排如下：第二節設計利用一致性分析的高維類別不平衡數據特征選擇的模型與算法；第三節對所提算法進行實驗驗證與結果分析；第四節總結全文.

2 利用一致性分析的高維類別不平衡數據特征選擇

在實際應用場景中，數據的樣本類別呈現多類及類別比例差異大等特點，而且小類樣本在眾多樣本中占據著舉足輕重的地位.為此，本文通過定義樣本的一致性來進行高維類別不平衡數據的特征選擇.首先，基于特征空間的樣本距離來定義目標樣本的近鄰，并根據目標樣本所在類別的數量來定義近鄰的大小；其次，定義目標樣本近鄰空間內類別一致的近鄰與論域中所有同類樣本的比例稱為包含度，包含度反應特征對樣本的區分與類別空間對樣本區分的一致性，而且能有效地避免小類樣本被大類樣本覆蓋的情況.基于該一致性，可以定義特征對類別標記的重要度，并設計相關的前向貪婪搜索算法.

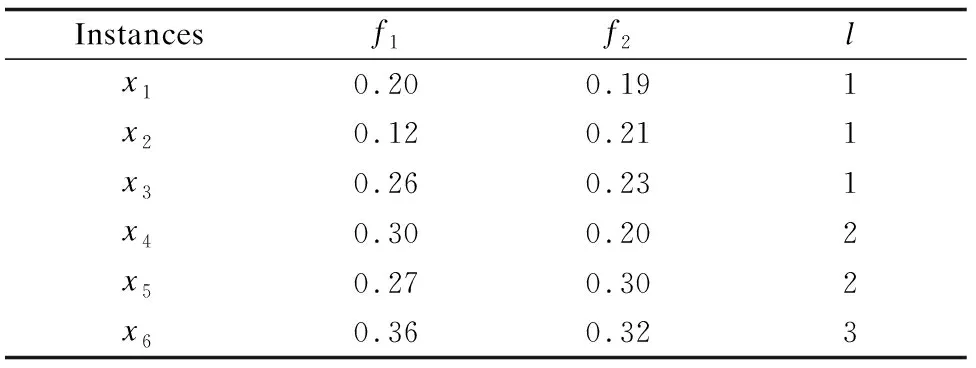
表1 高維類別不平衡數據示例表Table 1 Example of high-dimensional class-imbalanced data

定義1.給定論域空間內決策系統，U={x1，x2，…，xn}，標記L將U劃分為N個類別：L={X1，X2，…，XN}.?S?F，對于?Xj?L，nj是第j類樣本的數量，?xi∈Xj，定義xi在S下的κ-近鄰為

κS(xi)={x|x∈Minnj{ΔS(x，xi)}，x∈U}

(1)

其中，ΔS(x，xi)表示樣本xi與任意樣本的距離，Minnj{ΔS(x，xi)}表示與樣本xi距離最近的前nj個樣本的集合，如圖1所示.

例1.由表1所示，給定特征f1，樣本x1，因x1∈X1，有n1=|X1|=3，則Min3{Δf1(x，x1)}={x1，x3，x5}，所以目標樣本x1的近鄰空間為κf1(x1)={x1，x3，x5}.

圖1 實數空間中樣本的近鄰關系Fig.1 Near neighbor relationship of sample in real spaces

定義2.給定論域空間內決策系統，U={x1，x2，…，xn}，標記L將U劃分為N個類別：L={X1，X2，…，XN}.?S?F，對于?Xj?L，nj是第j類樣本的數量，?xi∈Xj，定義包含度函數為：

(2)

其中，κS(xi)表示樣本xi在特征子集S條件下的近鄰，Xj表示第j類樣本的集合，I(κS(xi),Xj)表示樣本xi的包含度.表明樣本xi由特征子集S誘導出的近鄰空間與類別誘導出的類別空間的包含程度.

例2.由表1所示，給定特征f1，樣本x1，因x1∈X1，有n1=|X1|=3，則x1的近鄰空間κf1(x1)={x1，x3，x5}，而κf1(x1)∩X1={x1，x3}，故I(κf1(x1)，X1)=2/3.

定義3.給定論域空間內的決策系統，對?S?F，定義特征子集S與標記L的一致性函數為:

(3)

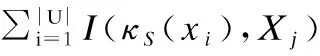
定義4.給定論域空間內的決策系統，S?F，?f∈F-S在特征子集S條件下，特征f的重要度為:

sig(f，S，L)=CONS∪f(L)-CONS(L)

(4)

標記對特征的包含度函數定義了特征對分類的貢獻，因此，可以作為特征集合重要性的評價指標.

根據定義4的特征重要度函數利用前向貪婪搜索算法依次對特征空間迭代直至終止條件得到的特征選擇結果即為最終選擇的特征.因此，本文將基于一致性函數，構造一種前向貪婪搜索特征選擇算法.該算法以空集為起點，每次計算全部剩余特征的特征重要度，從中選擇特征重要度值最大的特征加入特征選擇集合中，直到所有剩余特征的重要度為0，即加入任何新的特征，系統的一致性函數值不再發生變化為止.

根據以上分析，利用一致性分析的高維類別不平衡數據特征選擇算法具體描述如算法1所示.

算法1.利用一致性分析的高維類別不平衡數據特征選擇(Feature Selection of High-dimensional class-imbalanced data using Consistency analysis，簡稱FSHC)

輸入：

輸出：約簡后red

1. ?→red

2. ?f∈F-red/*計算樣本距離關系矩陣Nred和Nred∪f，若Nred=?，則不計算*/

3. fori=1，2，…，ndo/*n為總樣本數，即|U|=n*/

4.xi∈Xj，nj=|Xj|

5.κ(xi)=(x|x∈Minnj{Δ(x，xi)}，x∈U}

6.I(κ(xi)，Xj)=|κ(xi)∩Xj|/|κ(xi)|

7. end for

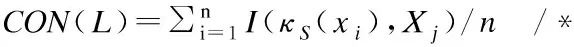
9. 計算sig(f，red，L)=CONred∪f(L)-CONred(L)

10. 選擇f′滿足sig(f′，red，L)=maxsig(f，red，L)

11. ifsig(f′，red，L)> 0 then

12.red∪f′→red

13. go to step 2

14. else

15. returnred

16. end if

算法1中第3-8步計算特征與標記的一致性值，第9-12步利用前向貪婪搜索策略對特征進行選擇.假設論域空間有n個樣本，f個特征，則該算法的時間復雜度為O(n·f2).

3 實驗結果與分析

3.1 實驗數據

為了驗證FSHC算法的有效性，選取12個高維數據集進行實驗，包括9個類別不平衡數據集和3個常規數據集，其中，brain、car、dlbcl、DrivFace、glioma、lung、lung2、lymphoma、srbct為類別不平衡數據集，colon、mll、prostate為常規數據集，描述信息見表2.對多類別數據集而言，由于類別存在對立的關系，當類別足夠多樣時，遍歷到某一類樣本即可視為小類樣本，假設為正類，其余類樣本即為異類，同理，遍歷其余類別樣本亦如此.

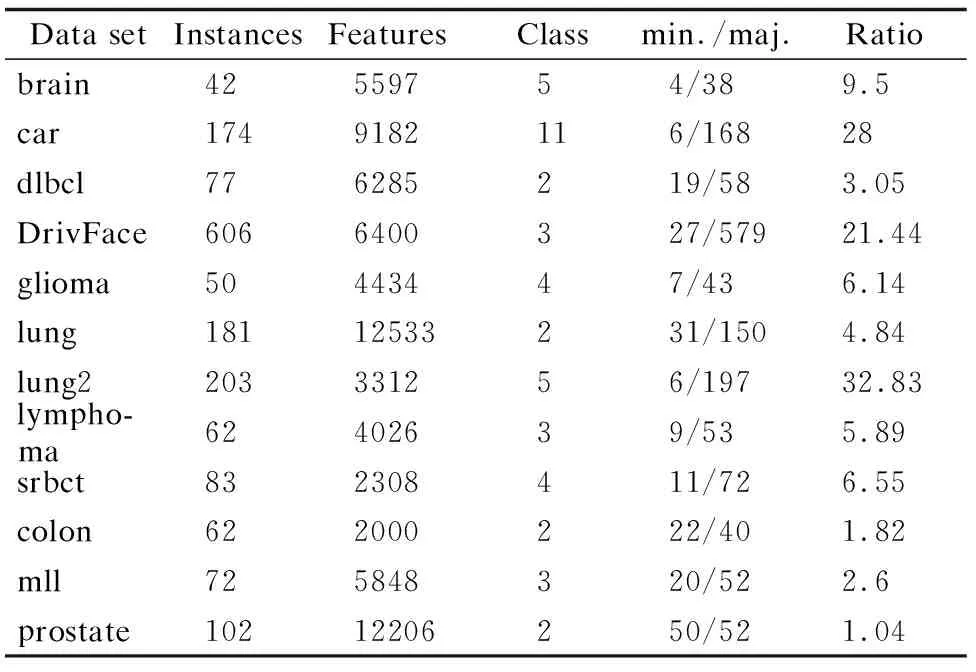
表2 類別不平衡數據集和常規數據集Table 2 Class-imbalanced data sets and routine data sets

為了更直觀地呈現數據集的相關信息，采用相關矩陣圖可視化高維數據的標記信息，矩陣圖用灰度刻畫類別及樣本數量，右邊細縱軸刻度代表類別，一種灰度表示一個類別，類別自下而上有序排列，左邊縱軸刻度代表樣本數量，樣本數自下而上遞增，一個色塊表示該類別擁有的樣本數量，詳見圖2.

3.2 評價指標

在高維小樣本數據的分類學習過程中，對分類精度而言，即使類別不平衡問題造成小類樣本的誤判，無法區分小類樣本的算法依然可以有比較高的精度，因此，本文實驗結果的評價指標采用F-Score、G-Mean、分類精度，其中，F-Score和G-Mean是兩個評價算法對于類別不平衡數據集小類樣本分類性能的重要指標.關于F-Score和G-Mean評價指標的正負例樣本的劃分，本文算法采用依次遍歷數據的樣本類別.假設當前遍歷到的類別為正類，則其余類別為異類，屬于正類的樣本為正例樣本，屬于異類的樣本為負例樣本.然后分別求各類別的F-Score值和G-Mean值，再求均值作為最終的F-Score值和G-Mean值.

設TP為真正例，TN為真負例，FP為假正例，FN為假負例，則查準率為P=TP/(TP+FP)，查全率為R=TP/(TP+FN)，F-Score定義為:

(5)

圖2 高維數據集的相關矩陣圖Fig.2 Correlation matrix of high-dimensional data sets

G-Mean定義為:

(6)

為了顯示算法的統計顯著性，使用基于算法排序的Friedman檢驗，假定在N個數據集上比較k個算法，令ri表示第i個算法的平均序值，定義Friedman統計量為:

(7)

其中，

(8)

若“所有算法的性能相同”的假設被拒絕，則表明算法的性能顯著不同，此時以Nemenyi后續檢驗進一步區分，Nemenyi檢驗計算出平均序值差別的臨界值域為:

(9)

3.3 實驗設置

本文實驗全部運行在3.10GHz處理器，4.00GB內存，windows 7系統及Matlab 2013的實驗平臺上.為減少因各特征量綱不一致對實驗結果造成影響，采用離差標準化將所有數據的屬性值歸一化到[0，1]區間.

表3 平均F-Score值Table 3 Average F-Score value

為了檢驗算法的有效性，實驗采用mRMR[10]、DISR[11]、NRS[12]等經典特征選擇算法，以及OSFS[13]、Fast-OSFS[13]、K-OFSD[7]、OFS[8]等在線特征選擇算法作為對比算法.基分類器為RBF-SVM，且采用5折交叉驗證.由于mRMR、DISR算法的特征選擇結果為特征排序，NRS、OSFS、Fast-OSFS、OFS、K-OFSD、FSHC算法的特征選擇結果為特征子集.為了公平比較，排序法算法mRMR、DISR特征排序中的特征數量設置為子集法算法NRS、OSFS、Fast-OSFS、OFS、K-OFSD、FSHC特征選擇結果中特征數最多的數目，并從第一個開始取.NRS的鄰域參數δ設置為0.1.OSFS和Fast-OSFS采用Fisher′s Z test方法度量特征的相關性，顯著性水平的參數α設置為0.01[14].K-OFSD和OFS中的近鄰參數k取7，特征與標記的相關性閾值β設置為0.5，OFS中參數n取4，以類別包含數量最少的樣本為小類樣本[7，8].

3.4 實驗分析

3.4.1 預測精度分析

實驗數據表3-表5分別給出了各算法在各數據集上特征選擇子集的平均F-Score值、平均G-Mean值以及平均分類精度和標準差.其中，標注黑體部分代表該算法在此數據集上的性能最優.

表4 平均G-Mean值Table 4 Average G-Mean value

由表3和表4可見，在類不平衡數據集brain上算法FSHC的分類性能遜于K-OFSD、OFS，在類不平衡數據集lymphoma上算法FSHC的分類性能遜于Fast-OSFS. 除以上兩個數據集外，算法FSHC的分類性能均優于對比算法.表5給出了特征選擇子集的平均分類精度和標準差，分類精度越高說明樣本分類越準確，標準差越小說明分類穩定性越高.不難看出，在平均分類精度方面，除了在類別不平衡數據集brain上算法FSHC的分類精度略遜于算法K-OFSD、OFS外，FSHC的分類精度均優于對比算法.

F-Score和G-Mean是兩個評價算法對小類樣本分類性能的重要指標，FSHC算法在這兩個評價指標上都獲得了很高的值，由此可見，利用一致性分析的高維類別不平衡數據特征選擇算法，相對于經典特征選擇算法或者在線流特征選擇算法在處理高維小樣本數據分類學習任務中的類不平衡問題方面具有更高效的表現能力.

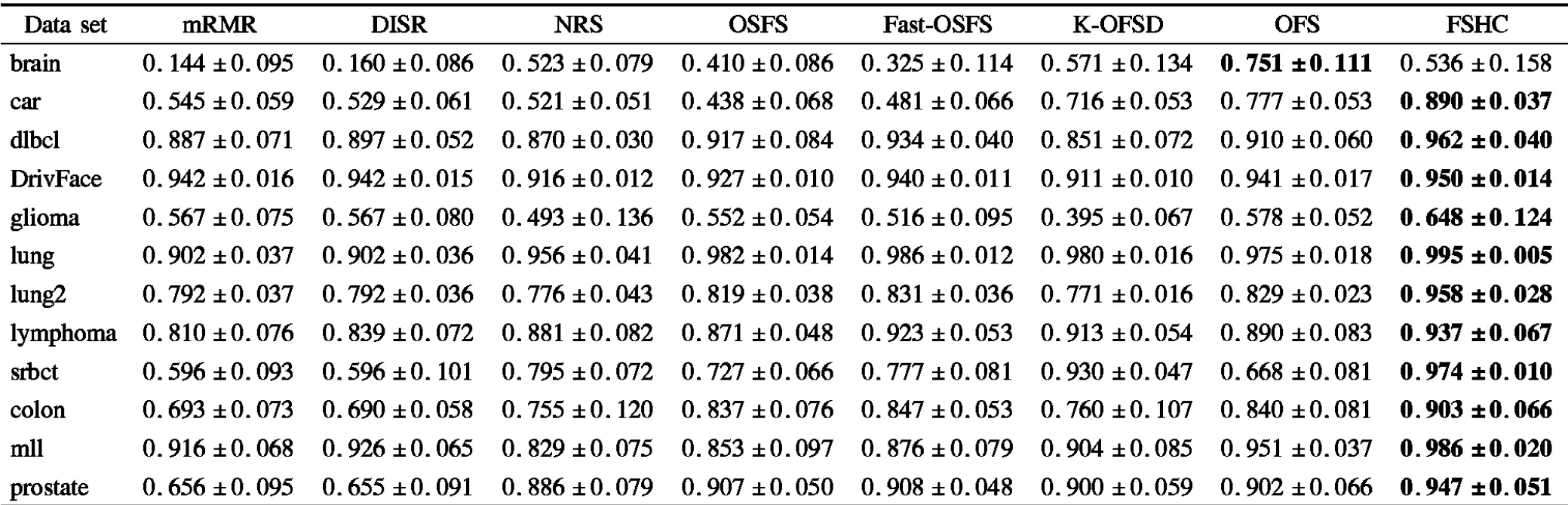
表5 平均分類精度和標準差Table 5 Average classification accuracy and standard deviation

3.4.2 統計性分析

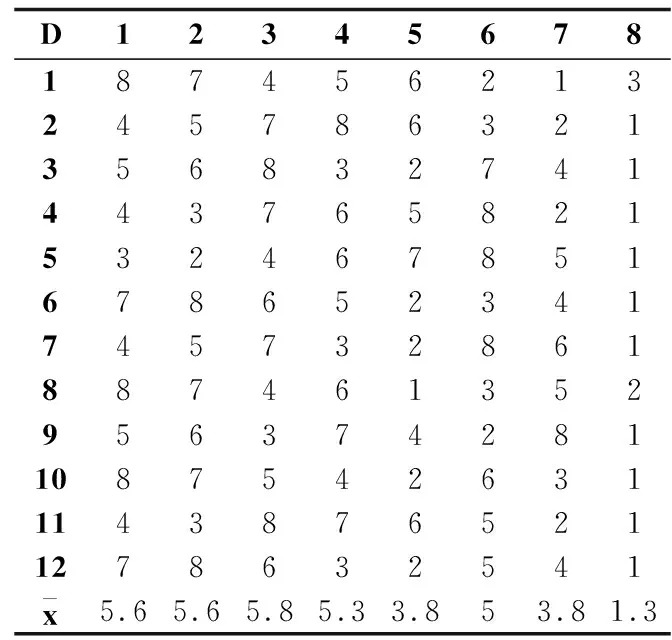
序值表6中的子表(a)-(c)分別根據表3-表5的測試結果給出了多數據集多算法在F-Score、G-Mean和分類精度評價指標上的算法比較序值表，各算法在每個數據集上根據測試性能由好到壞排序，并賦予序值，若算法的測試性能相同，則平分序值.表6橫軸的數字對應表3的表頭橫軸代表的算法，縱軸的數字對應表3的表頭縱軸代表的數據集，其中，最后一行表示各算法的平均序值.對表F檢驗參數alpha取0.05的常用臨界值表可知，8個算法12個數據集的臨界值為2.131，根據Friedman統計量公式，計算F-Score、G-Mean、分類精度的τF值分別為7.934、6.998、9.299，均大于F檢驗臨界值2.131，拒絕“所有算法性能相同”的假設，進行Nemenyi后續檢驗.對表Nemenyi檢驗參數alpha取0.05的常用qα值表可知，8個比較算法的qα值為3.031，根據Nemenyi檢驗的臨界值域公式，計算得到臨界值域CD為3.031.

由表6的平均序值可知，子表(a)、(b)、(c)算法FSHC與算法Fast-OSFS 、OFS的差距均未超過臨界值域，說明算法FSHC與算法Fast-OSFS 、OFS的性能沒有顯著差別.而算法FSHC顯著優于算法mRMR、DISR、NRS、OSFS、K-OFSD，因為算法FSHC與算法mRMR、DISR、NRS、OSFS、K-OFSD的差距超過了臨界值域.

上述比較檢驗可以直觀地用弗里德曼檢驗圖顯示，圖3中的子圖(a)-(c)的弗里德曼檢驗圖分別由表6中的子表(a)-(c)導出，橫軸表示各算法的平均序值，縱軸表示算法，對應表6的算法序號，其中，第8號純黑線表示算法FSHC的平均序值和臨界值域.對每個算法，用圓點顯示其平均序值，以圓點為中心的橫線段表示臨界值域的大小，于是可從圖中觀察，若兩個算法的橫線段有交疊，說明這兩個算法的分類性能沒有顯著差別，否則說明其性能有顯著差別.也可以用灰度區分算法的性能，第8號純黑線為算法FSHC，對比其余算法，對比算法為深灰線，說明性能顯著不同，對比算法為淺灰線，說明性能沒有顯著差別.由圖3可見，子圖(a)、(b)、(c)純黑線8號算法FSHC與淺灰線5號算法Fast-OSFS 、7號算法OFS沒有顯著差別，因為它們的橫線段有交疊區域，對比算法灰度為淺灰，而算法FSHC顯著優于余下的算法，因為它們的橫線段沒有交疊區域，余下對比算法灰度為深灰.顯然，算法FSHC的平均序值均高于對比算法，說明FSHC的分類性能均優于對比算法.

表6 算法比較序值表Table 6 Ordinal table of algorithm comparison

(b)G-Mean index

(c)Accuracy index

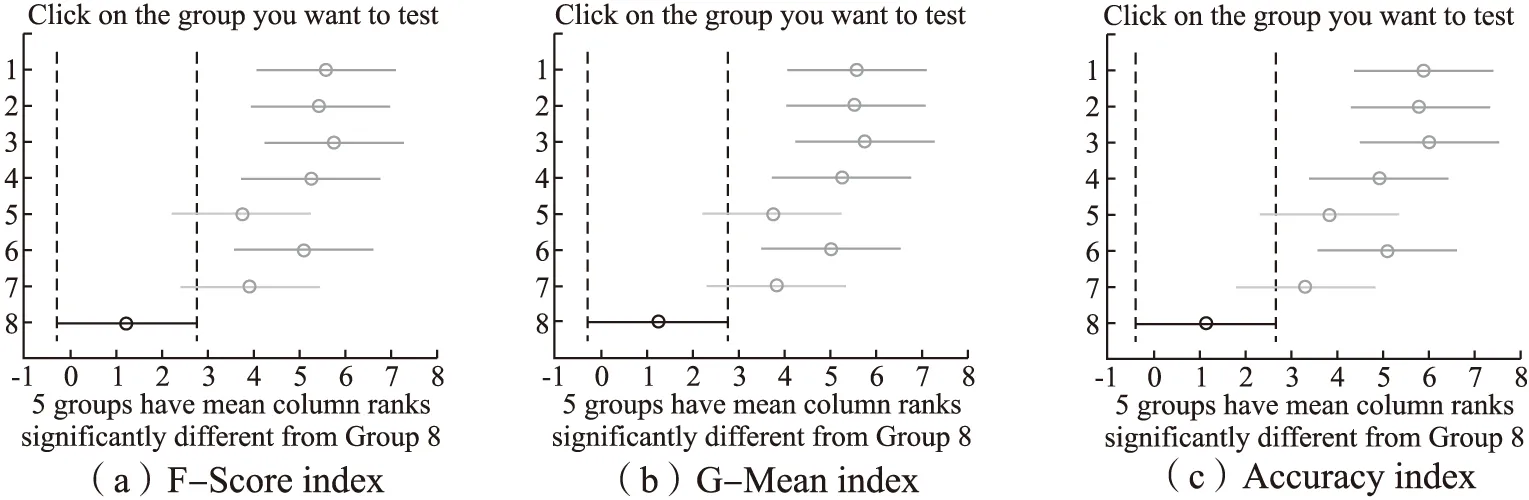
圖3 FSHC算法與對比算法的Friedman檢驗圖Fig.3 Friedman test diagram of FSHC algorithm and comparison algorithms

圖4 FSHC算法與對比算法的蜘蛛網圖Fig.4 Spider diagram of FSHC algorithm and comparison algorithms

3.4.3 穩定性分析

為了驗證不同算法的穩定性[15]，繪制蜘蛛網圖來表示多數據集多算法在各個評價指標上的穩定性指數.圖4中的子圖(a)-(c)分別給出了算法在F-Score、G-Mean和分類精度評價指標上的穩定性指數，其中，純黑直線代表算法FSHC的穩定性值.由圖4可見，對于F-Score和G-Mean而言，算法FSHC在6個數據集上接近穩定解，在類別不平衡數據集brain、DrivFace、glioma、lymphoma上穩定性較弱.

4 結束語

在高維類別不平衡數據特征選擇過程中，為了獲得在小類樣本中具有高可分離性的特征，通過定義樣本的近鄰關系，計算樣本分布與類別空間的包含度，進而導出特征與標記的一致性，由此提出一致性分析模型，并構建了面向高維類別不平衡數據的貪婪搜索算法.實驗結果表明，本文所提的方法是有效的.