一種航空發動機壓氣機喘振檢測方法

申世才，雷 杰，郝曉樂

(中國飛行試驗研究院發動機所，西安，710089)

喘振是一種危害性極大的發動機壓縮系統氣動失穩現象，輕則造成發動機工況急劇惡化,重則導致發動機機械損傷，進而引發嚴重飛行事故，引起人員和財產的巨大損失[1]。因此，尋求一種快速、準確檢測發動機喘振故障的方法是發動機穩定性研究領域的熱點問題，對于保障航空器飛行安全具有重要的現實意義和價值。

當前，國內外的喘振檢測方法基本是以壓氣機出口流場壓力為對象，根據壓力信號時域或頻域特征進行喘振算法研究。其中基于壓力信號時域特征的喘振檢測算法主要有：自相關函數法[2]、短時能量法[3]、變化率法[4-5]、壓差法[6]、方差分析法[7]、統計特征法[8]等，基于壓力信號頻域特征的喘振檢測算法主要有：頻譜分析法[9-11]、小波分析法[12-13]、頻域幅值法[14-15]等。上述時域和頻域特征喘振檢測算法多數是以壓氣機部件級試驗為支撐，取得了很多較好的喘振檢測效果，但由于受到試驗對象和條件限制，應用在發動機整機喘振檢測的算法相對較少，有必要尋求一種簡單、可靠、準確的發動機整機喘振檢測方法。

1 壓氣機出口脈動壓力統計特征分析

發動機壓氣機出口動態壓力p31包含平均壓力成分p31.a和脈動壓力成分Δp31，在發動機穩定狀態下，壓力機內部流場穩定，其出口脈動壓力Δp31相對穩定，而在發動機出現喘振時，壓氣機出口流場Δp31呈不穩定狀態[4]。所以當發動機穩定工作時，如果Δp31服從某種概率分布規律，根據其概率分布函數，就可以通過Δp31的統計特征設置閾值來檢測發動機喘振故障的發生。

正態分布是統計學中最重要的一種分布規律，大量隨機現象可以用正態分布規律來描述或近似，同時正態分布具有很多優良的性質，所以不論是在理論研究還是工程實踐中，正態分布具有廣泛的應用。這里首先假設Δp31測量數值服從正態分布，下面采用某發動機實測數據檢驗壓氣機出口脈動壓力時間序列數據是否符合正態概率分布規律。

某發動機試飛期間，測量了不同飛行高度、速度條件下發動機穩態及瞬態的p31時間序列數據，獲取了相應的Δp31時間序列數據。將這些不同飛行條件下發動機穩態和瞬態Δp31時間序列數據作為總體統計量，采用簡單隨機抽樣原則從總體統計量中抽取發動機穩態和瞬態Δp31時間序列數據作為檢驗樣本，進行Δp31時間序列正態符合性檢驗分析。

樣本數據x的正態性檢驗方法有很多，主要分為統計圖法和統計指標法。統計圖法包括直方圖、P-P圖、箱式圖、概率圖、分位數圖等，均能為樣本正態性提供一個粗略估計，本文采用分位數圖對樣本Δp31正態性進行初步估計；統計指標法可對樣本正態性進行定量檢驗，主要包括偏度峰度聯合檢驗、S-W(Shapiro-Wilk)檢驗、A-D(Anderson-Darling)檢驗、K-S(Kolmogorov-Smirnov)檢驗等，本文選擇K-S檢驗作為樣本Δp31的正態性定量檢驗方法。

圖1為高壓轉速為n2時發動機穩態過程Δp31時間序列隨機樣本分位數圖，可見該發動機穩態輸入樣本散點不完全分布在直線附近，故而不能完全為正態分布提供粗略支持，進一步采用K-S檢驗。

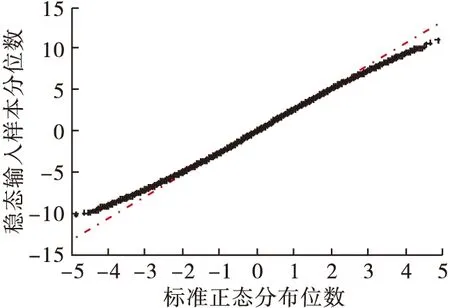
圖1 穩態過程時間序列樣本數據分位數圖

K-S檢驗統計量為：

Dn=max{|Fn(xi)-F0(xi)|,|Fn(xi+1)-F0(xi)|}

(1)

式中：Fn(x)為樣本的概率分布函數；F0(x)為標準正態分布函數。如果檢驗統計量Dn大于給定顯著水平α和樣本容量n確定的檢驗臨界值Dn(α)，則拒絕零假設，否則接受零假設，認為Δp31符合正態分布。

對圖1中發動機穩態過程時間序列樣本Δp31進行計算，得到Dn=0.008 3，取顯著性水平α為0.01時，查表得到臨界值Dn(α)=0.002 5，Dn>Dn(α)，故拒絕零假設，所以發動機穩態過程Δp31不服從正態分布。

進一步分析發動機瞬態過程Δp31是否服從正態分布，圖2為發動機瞬態過程Δp31隨機樣本分位數圖，顯然發動機瞬態過程Δp31輸入樣本散點同樣不完全分布在直線附近，進一步進行K-S檢驗：Dn等于0.014 7，取顯著性水平α為0.01時，查表Dn(α)為0.004，Dn>Dn(α)，拒絕零假設，故發動機瞬態過程Δp31同樣也不服從正態分布。

圖2 瞬態過程時間序列樣本數據分位數圖

進行全部Δp31時間序列樣本正態符合性檢驗后，發現Δp31不服從正態分布，這是因為發動機壓氣機是高溫、高速旋轉機械部件，其Δp31信號包含了發動機轉子頻率、葉片頻率的基頻和倍頻成分及受發動機瞬態過程影響，其測量數據隨時間統計序列不服從正態分布，所以對于Δp31這種未知分布規律，難以根據其統計特征設置喘振檢測閾值，想要Δp31按正態分布設置喘振檢測閾值，必須將Δp31時間序列樣本數據進行正態轉換。

2 壓氣機出口脈動壓力正態轉換

2.1 Johnson正態轉換方法

常用的非正態數據正態轉換方法主要包括：倒數轉換、對數轉換、平方根轉換、平方根反正旋轉換、平方根后取倒數轉換、Johnson轉換等，其中前5種方法對樣本數據的要求較高，要求樣本x為正值，由于Δp31存在負值數據，故難以采用前5種轉換方法對Δp31數據進行正態轉換。

Johnson轉換條件相對寬松，允許樣本x存在負數的情況，具有良好適應性且Johnson轉換可將隨機樣本x直接轉換為標準正態分布N(0,1)。本文采用Johnson轉換方法對Δp31時間序列樣本數據進行正態變換。樣本x進行Johnson正態轉換時，其基本轉換公式為：

z=γ+ηf(x,ε,λ)

(2)

式(2)中f(x,ε,λ)為特定Johnson分布曲線函數，具體為SB(有界)、SL(對數正態)、SU(無界)3種類型，η、γ、λ、ε等通過對應轉化類型計算公式得到，3種類型函數及參數約束條件見表1。

確定Johnson轉換函數的方法有很多，其中樣本百分位數法得到了廣泛應用，本文采用百分位數法進行正態轉換。

首先選擇一個合適的r,在標準正態分布表中查找(-sr，-r，r，sr)的分布概率P-sr、P-r、Pr、Psr，通過樣本獲取對應分位數x-sr，x-r，xr，xsr后，計算m=xsr-xr、k=x-r-x-sr、l=xr-x-r，得到分位數比mn/l2。

當mk/l2<1時為SB分布，mk/l2=1時為SL分布，mk/l2>1時為SU分布。由于分位數比與s和r取值有關，需要確定合適的s和r，研究表明s取值為3及r取值范圍為(0.25，0.26，…，1.25)時，可獲得較好的轉換效果[16-17]。

本文取r值為1.2(在0.25～1.25范圍內，r取值1.2時正態轉換效率最高)，對于圖1和圖2中發動機穩態和瞬態過程隨機樣本，計算得到mk/l2值分別為0.721和0.921 5，即mk/l2<1，Δp31的Johnson轉換函數為SB型，對應的η、γ、λ、ε計算公式為:

(3)

(4)

(5)

(6)

2.2 Johnson正態轉換結果

采用K-S方法對正態轉換后的脈動壓力時間序列樣本Δp31.norm正態性符合性進行檢驗。其中圖1所示發動機穩態過程Δp31.norm檢測結果為：Dn=0.001 1，Dn(α)=0.002 5，DnDn(α)，拒絕了零假設，故Johnson正態轉換后的瞬態Δp31.norm不服從正態分布。

對其他隨機樣本采用Johnson轉換并檢測轉換后Δp31.norm的正態性，發現Johnson轉換方法對于穩態過程具有較高的轉換效率，穩態過程Δp31.norm正態轉化成功率P可達到90%以上，但是對于瞬態過程隨機樣本正態轉換效果較差，瞬態過程Δp31.norm正態轉化成功率P不足50%。

進一步分析瞬態過程Δp31正態轉化率不足的原因：樣本Δp31是時間序列的統計量，其受發動機狀態變化影響很大，當發動機穩態工作時，Δp31幅值范圍基本穩定在同一量級，而不同轉速時Δp31幅值范圍差異較大，且在瞬態變化過程中，隨著發動機轉速的提高，Δp31幅值變化范圍也逐漸升高(具體如圖3所示)，這種Δp31幅值隨轉速變化的特性是導致瞬態過程Δp31隨機樣本Johnson正態轉化成功率P過低的主要原因。

為解決發動機瞬態過程Δp31正態轉換成功率P過低問題，必須降低瞬態過程轉速變化對于Δp31幅值變化范圍的影響，考慮到樣本Δp31是時間序列的高頻采集信號，其采樣頻率為5 kHz，減小Δp31樣本容量n就可以直接削弱轉速變化對于Δp31幅值變化范圍的影響，當樣本容量n減小到一定程度時(如幾十毫秒量級)，可假設認為發動機瞬態過程時間序列Δp31相當于一個準穩態變化過程。按照上述方法，逐步減小隨機樣本容量n，從總體樣本抽取幾十組發動機瞬態過程隨機樣本進行Johnson正態轉換，正態轉化成功率P統計情況見表2所示，可見減小樣本容量n可有效提高瞬態過程Δp31的正態轉化成功率，當隨機樣本量n降低至500及以下，隨機樣本Δp31的Johnson正態轉換成功率達到90%以上，因此要實現瞬態過程Δp31有效正態轉換，可將樣本容量n確定為100。

表2 瞬態過程正態轉化成功率統計表

3 喘振檢測閾值和方法

3.1 喘振檢測量

正態轉換后的Δp31.norm～N(0,1)，根據其概率分布函數可知，Δp31.norm時間序列落在±3.5范圍內的概率為99.95%，即Δp31.norm有99.95%概率分布在-3.5≤Δp31.norm≤3.5范圍內，那么根據表1中SB型Johnson轉換函數的反函數z-1，可以得到正態轉換前Δp31的99.95%概率分布范圍為：

(7)

由于瞬態過程Δp31樣本容量n不宜過大，當n過大時將不能有效實現Δp31正態轉換，所以也就不能通過Johnson轉換函數的反函數z-1獲取Δp31的99.95%概率分布范圍。此外，不同發動機狀態下Δp31幅值范圍存在較大差異，導致其99.95%概率分布范圍不同，進而不能根據Δp31分布范圍使用固定喘振檢測閾值。為解決這一問題，本文采用一種基于滑動窗口的Johnson轉換方法，具體如下。

假設滑動窗口長度為d，將測取的發動機時間序列Δp31第1點數據x1作為滑動窗口起始點，向后截取d個Δp31數據。對窗口內d個Δp31數據進行Johnson正態轉化，得到SB型Johnson正態轉換函數反函數的η、γ、λ、ε等參數，根據公式(7)計算窗口內Δp31數據99.95%概率分布上界Δp31.max和下界Δp31.min。將Δp31.max、Δp31.min作為第xd點時間序列Δp31的99.95%概率分布上界Δp31.max(xd)和下界Δp31.min(xd)。按照Δp31時間序列順序滑動計算窗口，重復上述計算方法，可以得到Δp31的99.95%概率分布的自適應上界Δp31.max和下界Δp31.min，實際等效于Δp31上下“包絡線”。

樣本容量n為100時正態轉換成功率最高，取滑動窗口d=100，對于圖3所示Δp31時間序列樣本數據，其99.95%概率的Δp31.max、Δp31.min分布情況見圖4所示，局部放大情況見圖5，可見采用滑動窗口的Johnson正態轉換方法，能夠獲取時間序列Δp31的99.95%概率分布自適應上界Δp31.max和下界Δp31.min。

上文所述Δp31等效“包絡線”反映了其幅值變化范圍，可以根據Δp31上下“包絡線”間距D檢測發動機喘振，為消除D受發動機轉速變化的影響，定義一種無量綱的發動機喘振檢測量T31為：

(8)

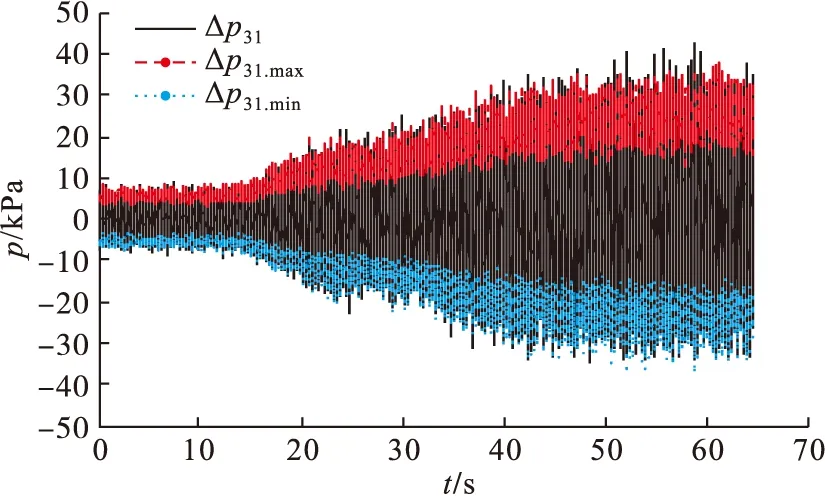
圖4 脈動壓力概率邊界時間序列

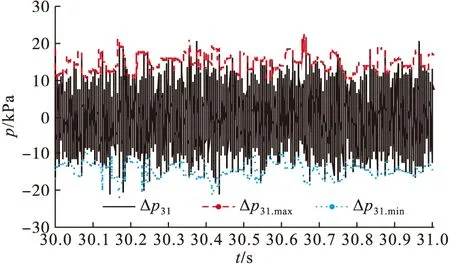
圖5 脈動壓力概率邊界時間序列局部放大圖

式(8)等效于對Δp31.max和Δp31.min間距D進行歸一化處理，可以消除發動機不同轉速時D幅值范圍的差異，便于設置固定的喘振檢測閾值。如對于圖4中所示的Δp31時間序列，其對應的喘振檢測量T31計算結果如圖6所示。

圖6 發動機無量綱喘振檢測量時間序列

3.2 喘振檢測閾值及方法

設置發動機喘振檢測閾值時，將上文不同飛行條件下發動機穩定工作時測取的穩態和瞬態時間序列Δp31作為總體統計量，采用滑動窗口的Johnson轉換方法計算對應的喘振檢測量T31，將獲取的T31作為設置喘振檢測閾值A的總體樣本。

采用K-S方法檢驗總體樣本T31正態性，表明其并不服從正態分布。對總體樣本T31進行Johnson轉換，即T31.norm～N(0,1)。對于轉換后的T31.norm，其同樣有99.95%概率分布在±3.5范圍內，由公式(7)計算發動機穩定工作時T31變化范圍為：

0.018 5≤T31≤0.079 8

(9)

因為當發動機喘振時，Δp31脈動幅值會迅速增大，其概率意義“包絡線”間距D必然會出現劇增，那么T31將不可避免超出0.079 8的范圍，可以設置固定喘振檢測閾值A=0.079 8。但是發動機穩定工作時，T31還存在0.025%概率小幅超過0.079 8，所以綜合考慮喘振檢測靈敏度和誤報率，引入一個優化參數t(1≤t≤2)，設置保守的固定喘振檢測閾值為：A=0.079 8t，t根據實際喘振檢測效果設定，以最低喘振誤報率作為t取值依據。

綜上所述，根據發動機固定喘振檢測閾值A，本文設計的喘振檢測方法為：當喘振檢測量T31大于A時，認為發動機出現喘振；當T31小于等于A時，認為發動機工作穩定。

4 喘振檢測方法試驗驗證

某發動機試飛期間先后發生3起喘振故障，其中地面發生喘振1次，空中發生喘振2次(記為空中喘振1、空中喘振2)，地面發動機喘振發生在穩態過程中，空中2起喘振分別發生在加速、減速過程中，使用該型發動機喘振試飛數據對喘振檢測方法的實際效果進行試驗驗證。

圖7～9為該發動機3次喘振檢測驗證結果，3次喘振檢測均發出了喘振信號。當發動機穩定工作時，不管是穩態過程還是瞬態過程，喘振檢測量T31變化幅值均相對穩定，不受發動機轉速變化影響，T31沒有超過檢測閾值A的范圍，而當發動機出現喘振時，喘振檢測量T31值會出現劇增并超過檢測閾值A。圖7所示發動機穩態過程，喘振時，從脈動壓力Δp31出現波動到發出喘振信號用時約為12 ms，喘振期間T31最大值增長至1.748；喘振消失時，從脈動壓力Δp31停止波動到喘振信號消失用時約為14 ms。圖8、圖9所示發動機瞬態過程，喘振時從脈動壓力Δp31出現大幅波動到發出喘振信號用時分別約為16 ms、15 ms，喘振期間T31最高增長到1.653和1.689；喘振消失時從脈動壓力Δp31停止波動到喘振信號消失用時分別約為17 ms、14 ms。

綜上所述，本文發動機喘振檢測方法成功檢測出3次喘振故障，其識別發動機喘振及退出喘振所需時間均小于20 ms，未出現虛警、漏報等異常情況，驗證了檢測方法的有效性和準確性，表明方法具有識別率高、報警遲滯小等優點。

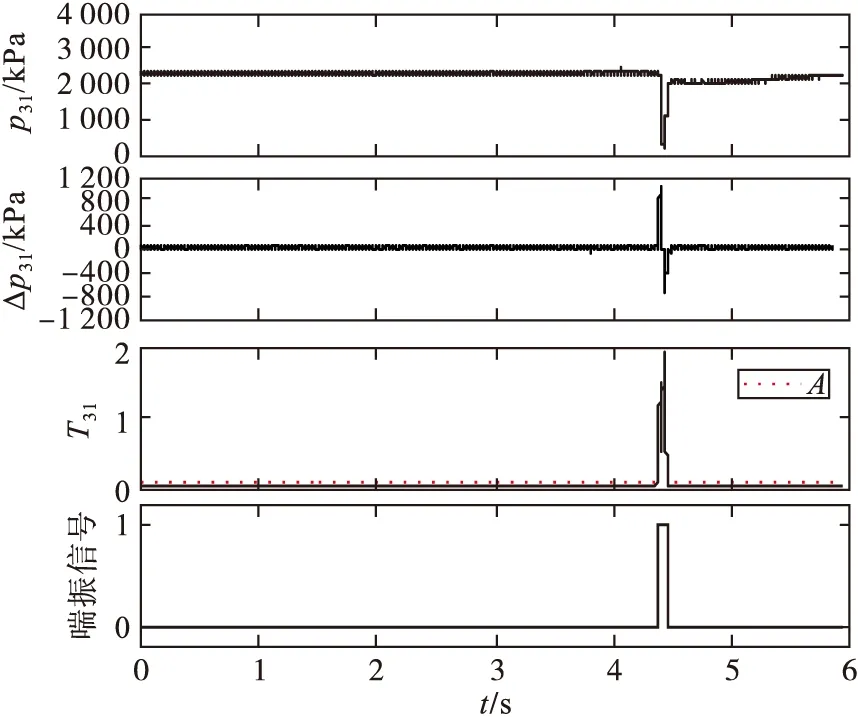
圖7 發動機地面喘振檢測結果

圖8 發動機空中喘振1檢測結果

圖9 發動機空中喘振2檢測結果

5 結論

1)在地面及空中發動機穩定工作時，壓氣機出口脈動壓力不服從正態分布。對于穩態過程脈動壓力，采用Johnson方法的正態轉換成功率較高，可達90%以上，但是對于瞬態過程正態轉換效果較差，當樣本容量n降低至500以下時，瞬態過程脈動壓力正態轉化成功率可達到90%以上。

2)采用滑動窗口的Johnson轉換方法，可以獲取壓氣機出口脈動壓力99.95%概率分布的自適應上邊界和下邊界。在不同發動機轉速下，該上、下邊界距離的幅值范圍差異較大，且隨發動機轉速增大而增大。

3)在地面及空中發動機穩定工作時，提出的喘振檢測量消除了發動機狀態變化帶來的影響，在穩態及瞬態過程中變化范圍差異很小，即喘振檢測量不受發動機工作狀態變化的影響。

4)根據喘振檢測量能夠設置適應發動機任意狀態的固定喘振檢測閾值，通過3次喘振試飛數據的驗證，其識別發動機喘振及退出喘振所需時間均小于20 ms，表明喘振檢測方法具有識別率高、報警遲滯小等優點。