星-彈雙基SAR建模及成像特性分析

郭 蘋, 焦曉陽, 王安義, 王 靜

(西安科技大學通信與信息工程學院，西安，710054)

隨著低成本火箭發射技術、微小衛星平臺技術和載荷技術的迅猛發展，實現全球信息，特別是天基信息共享的“天地一體化”體系正在全世界范圍內引發廣泛研究[1]。雙基地合成孔徑雷達(BiSAR)將收發站放置在2個不同平臺上，結合了雙基雷達和SAR的特點，具有隱蔽性強、抗干擾、信息獲取豐富、可前視成像等諸多優點[2-5]。與傳統的BiSAR[6-9]不同，SMB-BiSAR的接收機安裝在距離戰場較近的導彈上，而發射機位于距離戰場較遠的空間衛星上，將衛星平臺獨特的空間特性與導彈的機動靈活優勢相結合，使得彈載SAR可以有效獲取包含背景在內的目標景象進行圖像匹配處理，實現精確定位、制導等功能，提高打擊能力。另外，導彈作為接收端無需發射大功率信號其被檢測概率大大降低，從而增強了系統的抗干擾、抗偵察能力[10]。在“天地一體化”體系的背景下，研究SMB-BiSAR成像很有意義。然而SMB-BiSAR的優勢是以結構復雜性為代價的，衛星如何協助導彈成像將成為新的挑戰。

在SAR成像研究中，成像機理、成像性能以及信號特性，可從理論上反映場景目標的成像可能性和分辨能力，且與后期成像算法的研究和系統參數的設計密切相關[10-11]。關于傳統BiSAR，例如機載BiSAR，星載BiSAR的研究起步較早，成像處理技術也相對比較成熟。在傳統的BiSAR系統中，飛行平臺通常要求做勻速直線飛行。無論對于發射平臺還是接收平臺，經典的雙曲線模型假設都可以很好地直接應用[5-6]。由于不同平臺結合帶來的優勢，近年來，關于混合BiSAR，例如星-機級聯SAR的成像特性及成像算法的研究也逐漸增多[12-13]。但是，考慮到收發平臺的復雜幾何結構及飛行特性，對于曲線飛行的衛星、飛機及導彈平臺而言，直接應用經典的雙曲線模型將會帶來較大的相位誤差，在文獻[14]和[15]中提出了利用切比雪夫多項展開式代替泰勒級數展開式的方法提高距離模型的精度。在文獻[8]中對星-機雙基地SAR的空間幾何關系及信號模型進行了研究。孫稚超等人對地球同步軌道星-機雙基SAR的性能以及構型設計進行分析，明確了在空間分辨率和成像信噪比約束下機載接收站的路徑規劃[12]。文獻[16]從模糊函數的角度，推導了通用雙基SAR的分辨率表達式。然而，與機載SAR相比，導彈運動存在較大空間三維速度和加速度，尤其在末端俯沖下降段，以導彈作為接收機的成像幾何構型會更加復雜[17-18]，但目前關于SMB-BiSAR這一雙基構型的研究較少。只有文獻[19]進行了簡單的研究。

本文針對SMB-BiSAR這一特殊成像體制，分別在地心固定坐標系和參考點本地坐標系中，構建空間幾何模型，對收發平臺的成像模型進行矢量描述，得到目標的距離歷程以及回波信號模型。然后，利用距離等值線與多普勒等值線的正交關系，對接收站的飛行路徑約束條件進行分析。最后，根據距離分辨率與多普勒分辨率及兩者梯度的關系，得到SMB-BiSAR距離和方位分辨率的計算公式，并進行仿真驗證。

1 空間幾何關系及信號模型

考慮衛星軌道差異、導彈機動飛行等復雜情形，相比于常規單、雙基模式，星/彈SAR幾何模型發生較大的變化，首先在地心固定坐標系中對SMB-BiSAR的空間幾何進行分析，得到衛星的位置矢量和運動矢量，然后選取在更適合成像處理的參考點本地坐標系中建立信號模型進行特性分析。圖1為SMB-BiSAR空間幾何關系。

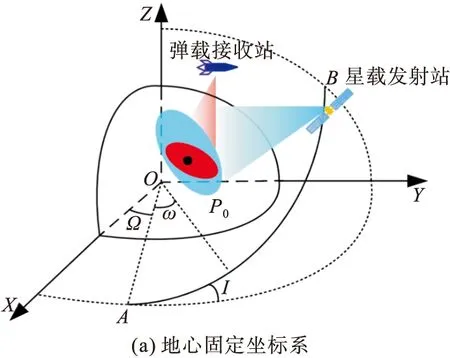
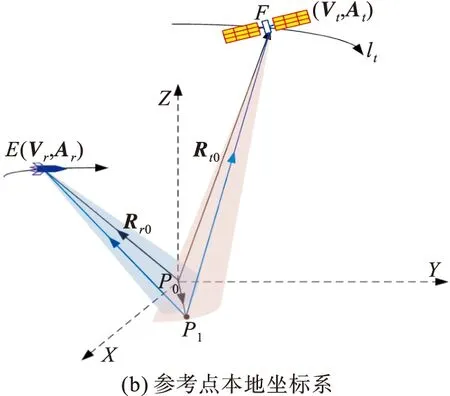
圖1 SMB-BiSAR空間幾何關系

由于在地心固定坐標系中進行距離歷程和回波相位的分析比較復雜，所以我們建立了參考點本地坐標系，如圖1(b)所示。在參考點本地坐標系中，波束中心點P0變為坐標原點，Z軸由地心指向參考點方向。

利用坐標系轉換，首先將地心固定坐標系繞Z軸逆時針旋轉θa，然后再繞Y軸順時針旋轉π/2-θe，最后沿Z軸將坐標系平移地球半徑長度Re，得到以波束中心為坐標原點的參考點本地坐標系。在該坐標系中，衛星的位置矢量Rt0和運動矢量(Vt,At)可以分別表示為：

(1)

式中：旋轉矩陣M0和M1分別可以表示為：

(2)

(3)

在合成孔徑時間內，衛星和導彈分別沿軌跡lt和lr運動。Pt是任意點目標P的位置矢量。點E和點F分別為參考時刻(η=0)發射站和接收站的位置。在任意方位η時刻，發射站和接收站的位置矢量分別為Rt(η)和Rr(η)，即:

(4)

式中：Rr0為接收站即導彈的初始位置矢量；Vr和Ar分別是導彈的速度矢量和加速度矢量。從物理學運動的角度出發，斜距模型是對雷達平臺與觀測目標之間相對運動的準確描述，因此，斜距建模是開展后續信號模型、多普勒參數分析、圖像幾何分辨率評估和成像方法等研究的必要條件。基于上述分析，在參考點本地坐標系中，任意點目標P的距離歷程可以表示為:

r(η)=|RT(η)|+|RR(η)|=

|Rt(η)-Pt|+|Rr(η)-Pt|

(5)

式中:|·|為取模操作符。

假設發射信號是線性調頻信號(LFM)，則目標的回波信號可以表示為：

(6)

式中：t為快時間；c為光速；λ為波長；ωr(·)和ωa(·)分別是距離和方位窗函數。

根據文獻[20]可知，利用泰勒級數展開對距離歷程進行矢量分析，其物理含義更明確，為了便于特性分析，將式(5)在η=η0時刻進行泰勒級數展開：

(7)

式中：κn是展開系數，κn(Pt)=μn(Rr0,Pt)+μn(Rt0,Pt)，則展開式可表示為：

(8)

式中：R是距離矢量。當R代表發射站距離矢量時，V和A指的是η0時刻發射站的運動參數；當R代表接收站距離矢量時，V和A表示為η0時刻接收站的運動參數。

如圖2所示，式(7)帶來的相位誤差的最大值遠小于π/4，這表示對距離模型采取三階泰勒級數近似帶來的相位誤差對最終成像質量造成的影響可以忽略。

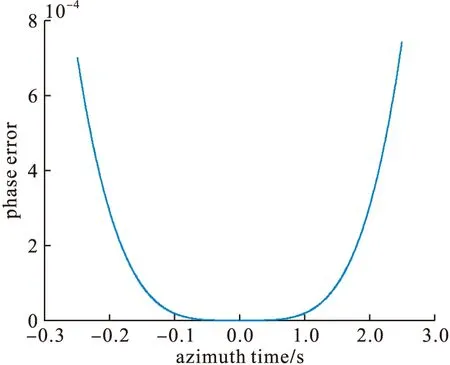
圖2 三階泰勒級數展開相位誤差

2 飛行路徑約束分析

在SMB-BiSAR系統中，衛星的運行軌道固定，但導彈的運動方式相對比較靈活，從而保證了系統的靈活性。作為SMB-BiSAR系統成像指標中重要參數之一，空間分辨率與收發平臺的相對位置、運動狀態都息息相關。文獻[9]中通過將無人機路徑規劃問題建模為多目標優化問題，獲得最適合的無人機路徑實現GEO-UAV星機雙基SAR成像任務。因此，為了保證在待成像區域獲得高分辨的二維成像，導彈的飛行路徑顯然也必須滿足一定的約束條件以獲得更好的空間分辨率。這里我們從雙基幾何構型的角度對導彈的飛行路徑約束條件進行簡單的分析。由于距離等值線和多普勒等值線在成像場景中的分隔特性可以反映在不同區域的成像能力，我們首先對距離等值線與多普勒等值線進行分析。在方位η時刻，場景中雙站距離和為Rη的距離等值線與多普勒頻率和為fdη的多普勒等值線可以表示為:

(9)

如果希望在待成像區域獲得高分辨的二維成像，要遵循的直觀構型設計原則是使得距離等值線與多普勒等值線正交或準正交[2]。由于梯度方向即距離等值線和多普勒等值線的法向量方向，所以我們首先分析兩者梯度的正交性。距離梯度和多普勒梯度可以表示為：

Rη=[|RT(η)|+|RR(η)|]=

UT(η)+UR(η)=U∑(η)

(10)

(11)

(12)

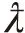
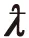
(13)

式中：0≤Ω≤π/2，可以利用式(13)設計BiSAR的幾何構型。當探測區域的Ω接近90°時，聚焦結果較好，反之聚焦性能降低。與單基SAR相比，BiSAR具有更為靈活的設計優勢，通過合理選擇系統幾何構型，使探測區域的Ω接近90°，獲得更好的等距線與等多普勒線的正交性。因此，可以根據Ω對導彈的飛行路徑進行簡單的約束限制。

3 空間分辨率分析

分辨率特性是BiSAR系統的重要理論基礎，該體制雷達的核心就是要獲取目標的高分辨率圖像。由于SMB-BiSAR與傳統的BiSAR模式不同，我們有必要對該新構型的距離和方位分辨率的計算公式進行新的推導。根據文獻[21]和[22]可知，距離分辨率與多普勒分辨率與兩者梯度有關，則距離分辨率可以表示為：

(14)

式中：Br是發射信號帶寬。將式(10)代入到式(14)可得：

(15)

式中：β是UT和UR之間的雙基地角。距離分辨率反映了2個點目標在距離方向上的分辨能力。當Br一定，ρr與雙基地角β有關。由于衛星和導彈的相對運動，在整個成像場景中的雙基地角是變化的，因此距離分辨率隨目標位置而變化。

SAR的方位分辨率是衡量多普勒頻率差異的能力。因此，多普勒頻率差對于方位分辨率的推導是重要的。由于方位分辨率與多普勒頻率的梯度有關[17]，可以表示為：

(16)

式中：Ta為合成孔徑時間。將式(11)代入式(16)，方位分辨率可表示為：

(17)

根據半角公式，可以得到：

|UT(Ta/2)-UT(-Ta/2)|=2sin(θT/2)≈θT

(18)

|UR(Ta/2)-UR(-Ta/2)|=2sin(θR/2)≈θR

(19)

式中：θT和θR分別是發射站和接收站的方位合成角或者相干積累角，分別與發射站和接收站的方位分辨率有關，則方位分辨率可表示為：

(20)

式中：eT和eR分別是發射站和接收站在方位方向上的單位矢量；α為eT和eR夾角。可以看出，方位分辨率由發射站和接收站的分辨率以及發射站和接收站的運動方向共同決定，我們可以通過設置合理的導彈運動方向，得到高分辨的SMB-BiSAR構型。

4 仿真分析

在SMB-BiSAR系統中，如果正確規劃了接收站的運動路徑，則可以構造多種成像模式。除了采用這種新型雙基地構型的傳統寬帶成像模式外，還可以實現前視和大斜視模式成像。這里首先對本文中飛行路徑約束的分析進行驗證，然后對SMB-BiSAR的前視分辨能力進行仿真，參考點本地坐標系中的收發平臺的參數信息由表1給出。

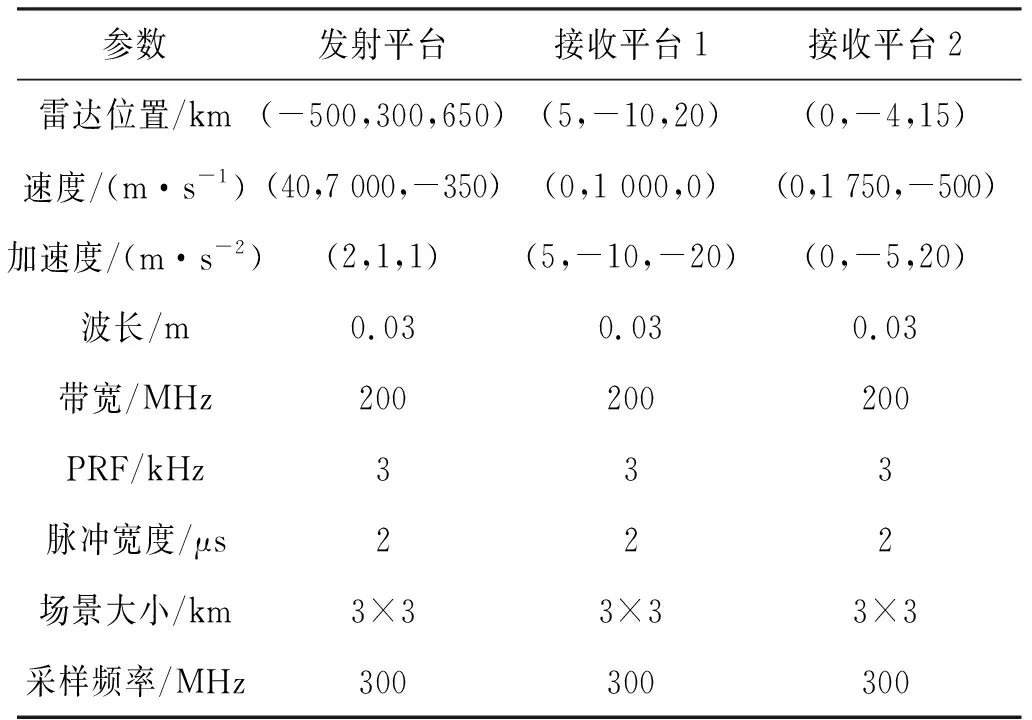
表1 仿真參數收發平臺參數信息

圖3表示利用表1中的參數進行仿真得到的SMB-BiSAR等距離/等多普勒線示意圖，圖中紫色五角星表示接收站，場景中心點位于坐標原點(0,0)位置。紅色虛線和黑色實線分別是距離等值線和多普勒等值線。在圖3(a)中可以看到，綠色條帶狀區域的距離等值線與多普勒等值線夾角Ω都相對較小，甚至接近零，這意味著該區域的距離方位耦合嚴重，對于回波數據的處理較難。而位于接收站大前斜方向的橢圓區域中，紅色和黑色線條構成的矩形或近似矩形區域表示距離等值線和多普勒等值線正交或者近似正交，這說明通過調整接收站的位置，SMB-BiSAR可以實現對成像區域的大前斜視成像。同理，由圖3(b)中可以看到，綠色條帶狀區域的距離等值線與多普勒等值線夾角Ω都相對較大，甚至接近180°，同樣說明該區域的距離方位耦合嚴重，難以實現二維成像處理。而位于接收站正前方的橢圓區域中，距離等值線和多普勒等值線正交或者近似正交，這說明SMB-BiSAR在前視模式下具有二維成像分辨率的能力。

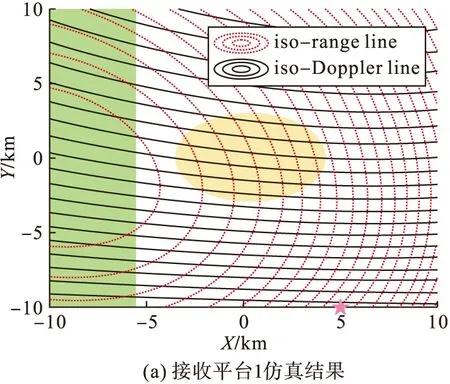
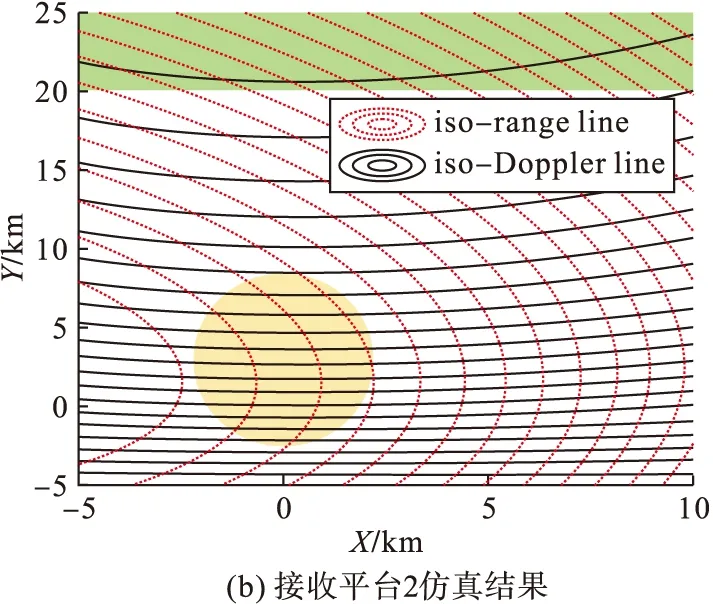
圖3 SMB-BiSAR等距離等多普勒線

為了驗證分辨率分析的正確性，利用表1中接收站1的參數，對距離分辨率和方位分辨率的計算進行仿真。由于距離分辨率與傳統雙基模式計算方法相同，這里只對距離分辨率與目標位置及雙基夾角的變化關系進行分析，如圖4所示。

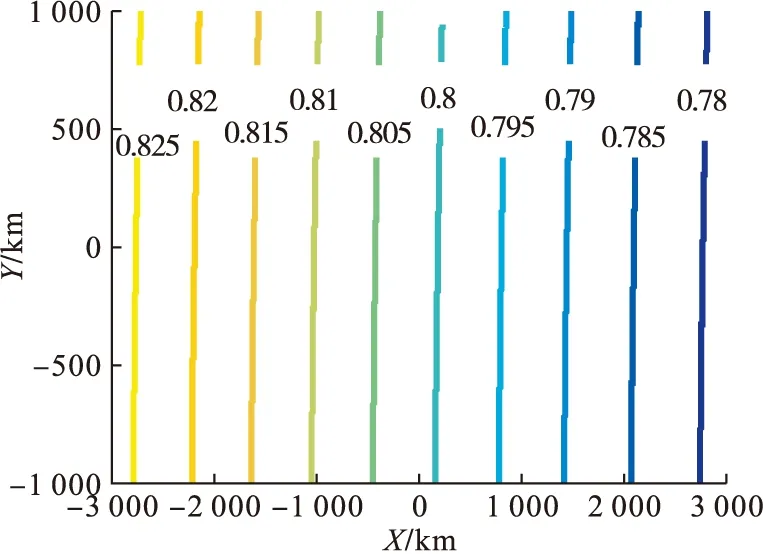
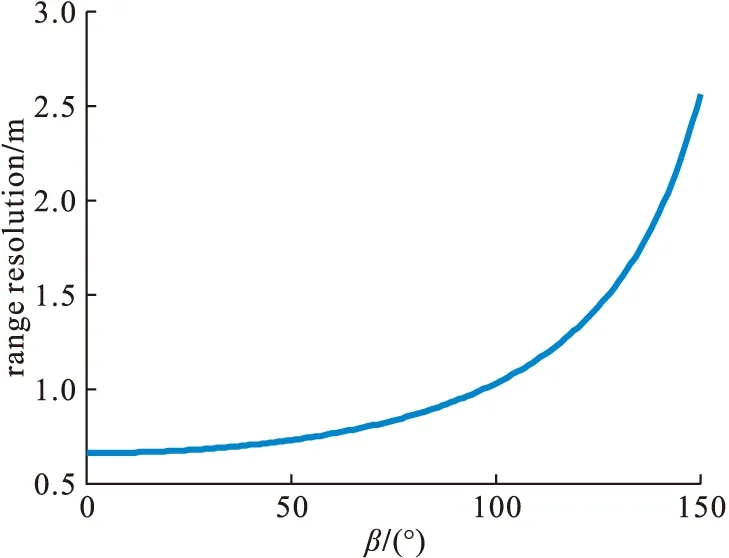
圖4 SMB-BiSAR距離分辨率

距離分辨率隨目標位置而變化，沿距離向變化大而沿方位向的變化小；另外，當發射站和接收站之間的夾角β越大時，距離分辨的效果越差，而當夾角β=0時，收發站位置重合，變為單基情況，距離分辨率效果最佳。

圖5給出了方位分辨率的計算結果，并利用后向投影算法(Back Projection Algorithm, BPA)聚焦結果進行對比。如圖5(a)所示,利用式(17)計算得到場景中心點目標(0,0)的分辨率數值為1.312 m，而根據3 dB波束寬度計算得到的方位分辨率理論值為1.311 m，如圖5(b)所示。通過對比可知，利用本文推導方法計算得到方位分辨率誤差為0.076%，滿足誤差要求。

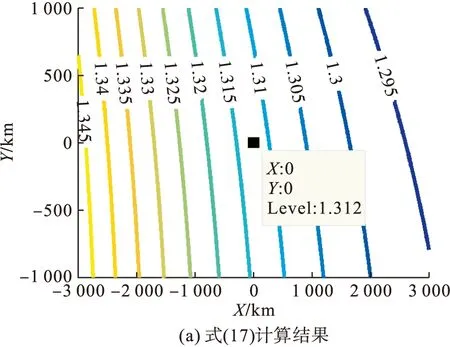
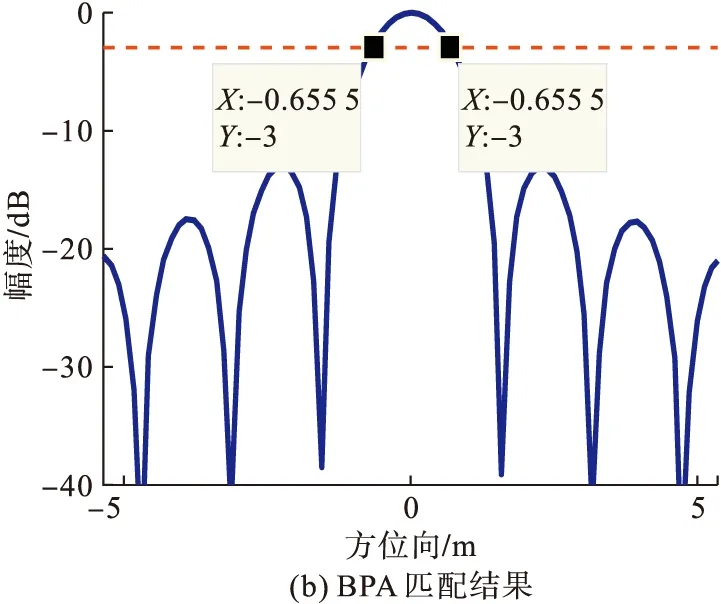
圖5 SMB-BiSAR方位分辨率

圖6給出了方位分辨率隨接收站和雙基角的變化示意圖，Y軸表示單基情況下導彈的方位分辨率，X軸表示夾角α。給定接收站的方位分辨率，當α小于某一數值時，SMB-BiSAR可以實現優于單基情況的分辨率。

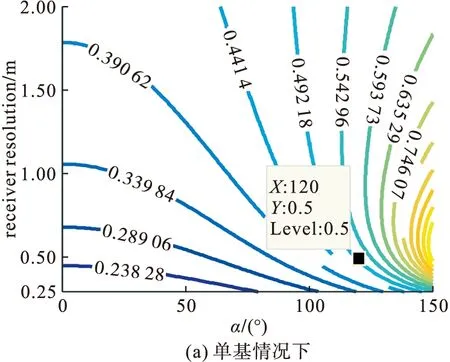
例如，假設單基情況下導彈的方位分辨率為0.5 m，當α小于120°時，SMB-BiSAR的方位分辨率優于單基情況的導彈方位分辨率。當單基方位分辨率大于1 m時，大部分情況SMB-BiSAR的方位分辨率是更優于單基導彈的方位分辨率。另外，由單基情況下導彈的方位分辨率ρα=1.14 m的方位分辨率圖可知，發射站和接收站運動方向的夾角越大，方位分辨率越差。當α=0時，發射站和接收站運動方向相同，方位分辨率效果最佳。

5 結語

SMB-BiSAR作為一種特殊的成像模型，將衛星平臺獨特的空間特性與導彈的機動靈活優勢相結合，可以實現對目標區域的精確定位、制導等功能。本文針對SMB-BiSAR這一特殊成像體制，分別在地心固定坐標系和參考點本地坐標系中，構建空間幾何模型，對收發平臺的成像模型進行矢量描述，得到目標的距離歷程以及回波信號模型。然后，利用距離等值線與多普勒等值線的正交關系，對接收站的飛行路徑約束條件進行分析，根據距離分辨率與多普勒分辨率與兩者梯度的關系，得到SMB-BiSAR距離和方位分辨率的計算公式。最后，通過仿真實驗對SMB-BiSAR的大前斜和前視成像能力進行驗證。仿真結果驗證了本文分析方法的有效性。