基于損傷等效理論的AC 25 kV腕臂型支持裝置疲勞程序譜編制

李梟俊,陳 展,吳積欽,張涵博

(西南交通大學電氣工程學院,成都 610031)

1 概述

疲勞程序譜為實驗室疲勞試驗中加載于被測試結構上的載荷，在開展疲勞試驗之前需制定剛性接觸網腕臂型支持裝置疲勞試驗程序譜[1]。

結合國內干線隧道剛性接觸網運行實際工況和不同位置定位點動應力與動態抬升時間歷程的分析可知，剛性接觸網腕臂型支持裝置所承受的載荷是典型的變幅載荷，若直接模擬現場載荷，其一是試驗耗時過長，其二是難以完全實現與現場相同的載荷譜[2]。開展腕臂型支持裝置疲勞試驗時應考慮高效且易實現。通過弓網動態仿真得到的動應力時間歷程，利用損傷等效理論，將仿真得到的疲勞振動載荷譜歸算為等幅載荷下疲勞試驗工況，既滿足高效性，同時也更易實現。要確定剛性接觸網腕臂型支持裝置疲勞試驗程序譜，一方面需要對腕臂型支持裝置的實際載荷進行細化；另一方面，損傷等效理論是針對材料的，若材料微觀層面的載荷與零部件級的載荷特征存在差異，則利用零部件級的載荷開展疲勞試驗將無法客觀反映材料損傷情況。故綜合以上分析，提出載荷譜的制定原則如下。

(1)精簡：疲勞程序譜需通過疲勞試驗臺實現，故疲勞程序譜越簡單越容易實現，在進行大量試驗時，更容易控制其偏差。

(2)損傷等效：損傷等效是疲勞試驗的核心，疲勞試驗結果應和實際情況相對應。

(3)高效：整個疲勞試驗耗時較長，故在滿足損傷等效的前提下，應盡量提高試驗效率。

2 損傷等效理論

2.1 損傷的定義

目前定義損傷變量主要有兩種途徑，其一是微觀的或物理的；其二是宏觀上的。從微觀上的角度定義疲勞損傷有多種方式，例如疲勞損傷區內微觀裂紋密度、電阻抗變化及纖維硬度變化等。從宏觀的角度定義疲勞損傷，主要為Miner疲勞損傷D=1/N、剩余剛度E、剩余強度、循環耗散能及阻尼系數等。

任何疲勞累積理論都是以疲勞損傷D的定義為基石，以疲勞損傷的演化dD/dn為基礎。一個合理的疲勞損傷理論其疲勞損傷D應該有明確的物理意義，有與試驗數據一致的疲勞損傷演化規律。

2.2 線性累積損傷理論

線性疲勞累積損傷理論是指在循環載荷作用下，疲勞損傷是可以線性累加的，各個應力之間互相獨立、互不相關，當疲勞損傷累加到某一數值時，時間或構件就出現疲勞破壞現象。線性累計損傷理論中最為典型的為Palmgren-Miner理論，簡稱Miner法則[3-4]。該理論具體內容如下。

(1)一個循環造成的損傷為

D=1/N

(1)

式中，N為當前載荷水平S對應的疲勞壽命。

(2)等幅載荷下，n個循環造成的損傷為

D=n/N

(2)

(3)變幅載荷下n個循環造成的損傷為

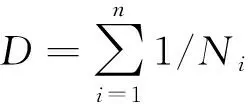
(3)

式中，Ni為當前載荷水平Si對應的疲勞壽命。

(4)臨界疲勞損傷DCR，若是等幅循環載荷，當循環載荷的次數n等于其疲勞壽命N時，疲勞破壞就發生，即n≈N，此時DCR=1。

2.3 雨流計數法

雨流計數法由M.Matsuishi和T.Endo于20世紀50年代提出，它根據載荷歷程得到全部的載荷循環，分別計算出全循環的幅值，并根據這些幅值得到不同幅值區間內所有的頻次，每個載荷循環在疲勞試驗中就對應一個應力循環[5-6]。

應用雨流計數法時應遵循以下4項規則：

(1)重新編排載荷歷程，以最高峰值或者最低谷值為雨流起點(視二者絕對值更大而定)；

(2)雨流依次從每個峰值或谷值內側往下流，直到遇到一個比其起點更高的峰值或更低的谷值時停下；

(3)當雨流遇到來自上層留下的雨流時立即停止；

(4)取出所有的全循環，記錄下各自的幅值和均值。

通過簡單例子對雨流計數法進行說明，如圖1(a)所示的載荷歷程，其起點并非最高峰值或最低谷值。故重新編排如圖1(b)所示的載荷歷程，將最高峰值點a作為重新編排的載荷歷程的起點，故a點之后的載荷歷程移動到c點前面，使c′與c點重合。

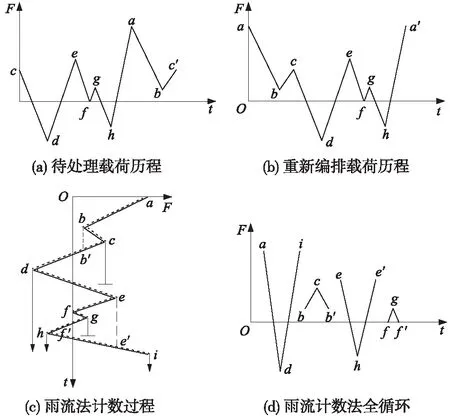
圖1 雨流計數法算例

把圖1(b)的載荷歷程順時針旋轉90°，得到圖1(c)，根據雨流計數法規則，對整個載荷歷程進行1次雨流計數，整個載荷歷程共計8個雨流，

分別為：(1)a-b-c-d,雨流從a點開始，為最小值，流至b點，下滴到b′點，然后停于d點；(2)b-c-d,雨流從峰值b開始，流經c，停于d；(3)c-b′,雨流從c點開始，由于遇到來自b點滴落的雨流，所以終止于b′點，組成一個全循環bcb′；(4)d-e-e′-i,雨流從d點開始，流至e點，下滴到e′點，然后停于i點；(5)e-f-f′-h,雨流從e點開始，流至f點，下滴到f′停于h點；(6)f-g-h,雨流從f點開始，流經g，停于h；(7)gf′,雨流從g點開始，由于遇到來自f點滴落的雨流，所以終止于f′點，組成一個全循環fgf′；(8)h-e′,雨流從h點開始，由于遇到來自e點滴落的雨流，所以終止于e′點，組成一個全循環eff′he′;而abb′d與dee′i又組成新的全循環abb′dee′i。至此，全部載荷歷程計數完成，形成如圖1(d)所示的4個全循環。

2.4 古德曼曲線

古德曼曲線是等壽命曲線中一種，具體內容是指受交變應力的結構，在等壽命的條件下，也即等破壞循環次數的情況下，一個應力循環中最大應力及最小應力與平均應力的關系曲線[7]。該曲線可以公式的形式描述，即為

S=Sa/(1-Sm/Su)

(4)

式中，S為等效應力；Sa為循環應力幅值；Sm為循環應力均值；Su為結構材料的強度極限。

通過古德曼公式可知，若已知變幅循環應力的應力幅值及應力均值，可將變幅應力循環等效為等幅應力循環。

3 載荷譜損傷等效方案的提出與驗證

3.1 載荷譜損傷等效方案提出

基于線性累積疲勞損傷理論、雨流計數法及古德曼等壽命公式，通過損傷等效的方式將變幅應力循環等效為恒幅應力循環，等效流程如圖2所示。

如圖2所示，存在任意一系列變幅應力循環，通過雨流計數法提取出變幅應力循環的各級應力循環均值、應力循環幅值范圍及應力循環的次數，得到三維的載荷譜，再利用古德曼等壽命公式將應力均值非零的變幅應力循環轉化為各級應力均值為零的等幅應力循環[8-10]。將各級的等幅應力循環組裝成為載荷塊，載荷塊作用于被測試件，通過線性累積疲勞損傷理論計算出被測試件的疲勞壽命，得到該載荷塊對試件造成的損傷量。與此同時，提取出一級循環，也即最大幅值循環將其組裝成等效載荷塊。同樣將等效載荷塊作用于被測試件，得到等效載荷塊對被測試件造成的損傷量，若以上兩個載荷塊的損傷量相等，即完成將一系列變幅應力循環等效為最大應力幅值的循環[11-14]。

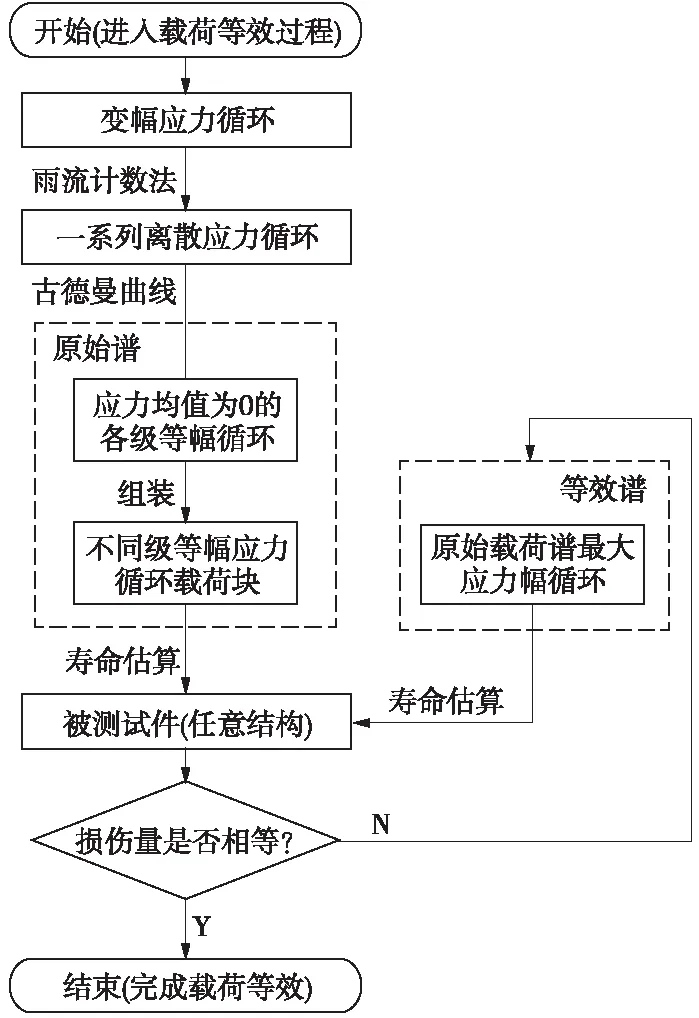
圖2 載荷譜損傷等效流程

3.2 具體等效方案

假設存在一系列隨機的應力均值非零變幅應力循環作為原始譜，如圖3所示。圖中各單次應力循環幅值依次為S1、S2、S3、…、Si，且應力均值非零。

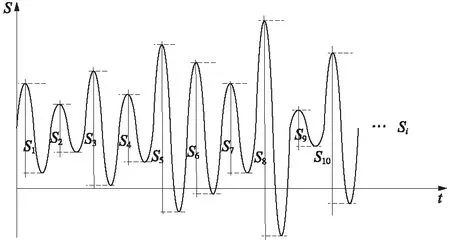
圖3 應力均值非零變幅應力循環

利用雨流計數法對圖3中一系列隨機的應力均值非零變幅應力循環進行計數統計，得到一系列離散的各級應力循環，并提取出各級應力循環的應力循環均值、循環應力幅值及循環次數[15]。雨流計數法得到上述一系列變幅循環的離散各級循環，以三維的形式呈現，圖4為一典型雨流計數法計算結果。圖中以各級循環應力的應力幅為X軸，應力均值為Y軸，循環次數為Z軸。

圖4 典型的雨流計數法計算結果

在雨流計數法計算結果的基礎上，利用古德曼等壽命公式，將雨流矩陣中各級的非零應力均值循環轉換成均值為零的各級等幅循環。通過式(4)可計算得到的各級應力循環等效幅值為

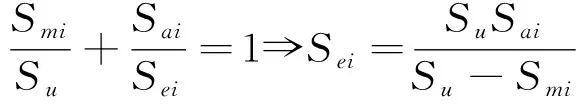
(5)

式中，Sei為第i級零均值應力循環的等效幅值；Su為被測試件材料的極限強度；Smi為雨流計數法計算結果中提取出的第i級循環的應力均值；Sai為雨流計數法計算結果中提取出的第i級循環的應力幅值。

在不考慮加載次序的前提下，將經古德曼等壽命公式計算后的各級等幅應力循環組裝成載荷塊，如圖5所示。

圖5 各級等幅應力循環的載荷塊

在得到由各級等幅應力循環組成的載荷塊的基礎上，利用線性累積疲勞損傷理論，計算出各級循環載荷下對被測試件造成的損傷量，整個載荷塊對被測試件造成的損傷量為各級循環載荷的線性疊加，如圖6所示，載荷塊損傷量表達式為

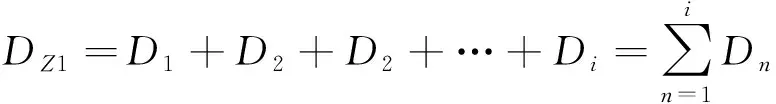
(6)

(7)

式中，Ni為被測試件在第i級等幅載荷循環下的疲勞壽命。

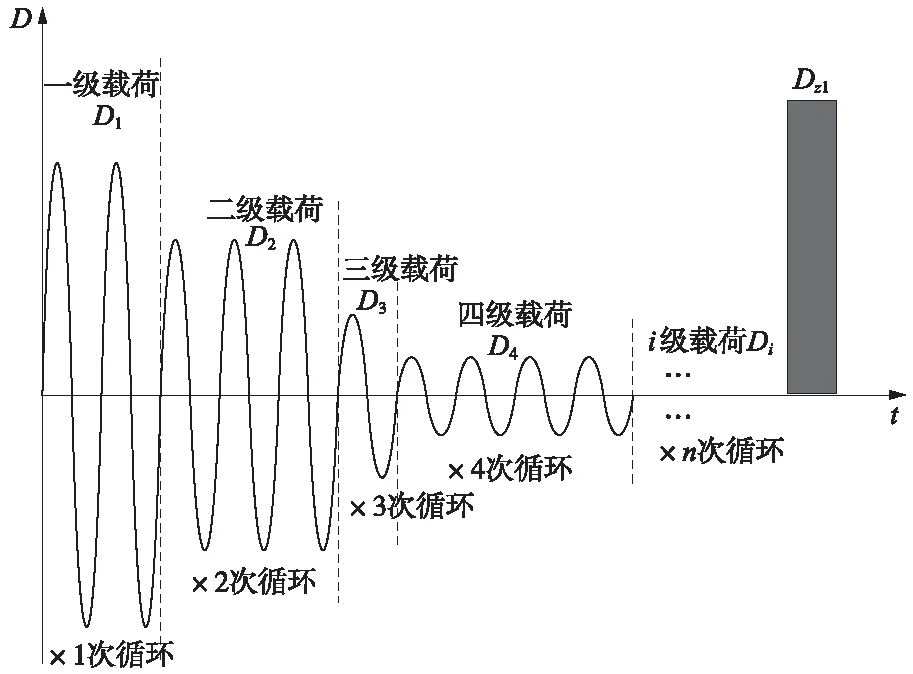
圖6 各級應力循環損傷量疊加圖

至此，即求出了一系列隨機的應力均值非零變幅載荷循環對被測試件造成的損傷總量，完成了圖2中原始譜的損傷計算。

提取出圖6中一級載荷循環組成等效載荷塊，如圖7所示，幅值為Sd=Se1。

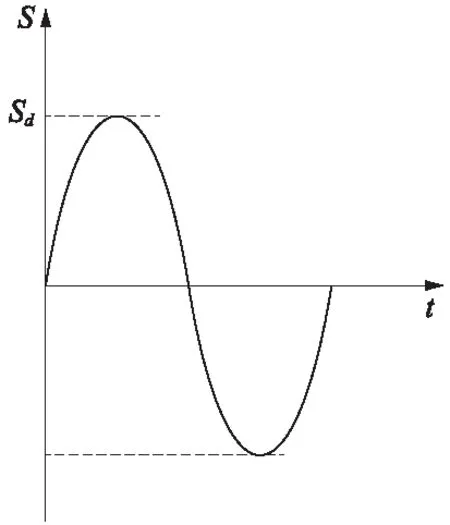
圖7 等效載荷塊

計算出等效載荷塊作用下，被測試件的疲勞壽命，通過古德曼等壽命曲線計算出等效載荷塊的損傷量。如圖8所示，等效載荷塊的損傷量為DZ2=D1。

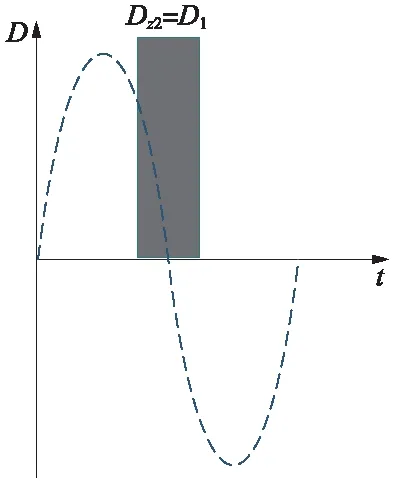
圖8 等效載荷塊損傷量

以上即為等效載荷塊的損傷總量計算，對比被測試件分別在等效載荷塊作用下的損傷量DZ2與原始譜作用下的損傷量DZ1，若DZ1≈DZ2，原始譜對被測試件造成的損傷總量可以通過等效載荷塊實現，即完成原始譜的轉化。

3.3 等效方案驗證

為驗證本文給出的損傷等效方案，通過Matlab軟件隨機生成3組初始載荷譜，計算初始載荷譜作用于試件產生的損傷量，再計算等效載荷塊作用于試件產生的損傷量，達到等效的目的。

(1)被測試件

被測試件是任意結構，故以一實心軸承柱作為被測試件，如圖9所示，軸承柱一端固定，載荷垂向作用于另一端。

(2)不同特征載荷譜

通過3.2中的分析可知，任何一系列隨機的應力均值非零變幅應力循環都可以通過雨流計數法和古德曼等壽命公式轉換為不同級的零均值應力的等幅循環。故為簡化計算過程，在Matlab軟件中生成3組零均值應力的載荷循環，分別為幅值遞增載荷循環、幅值遞減載荷循環及隨機載荷循環，將其作為原始載荷譜如圖10所示。

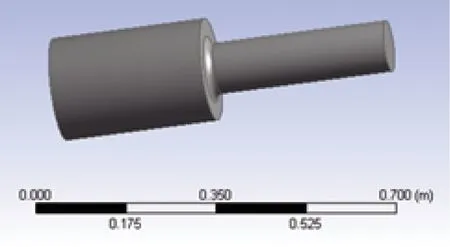
圖9 用于等效方案驗證的被測試件實體模型

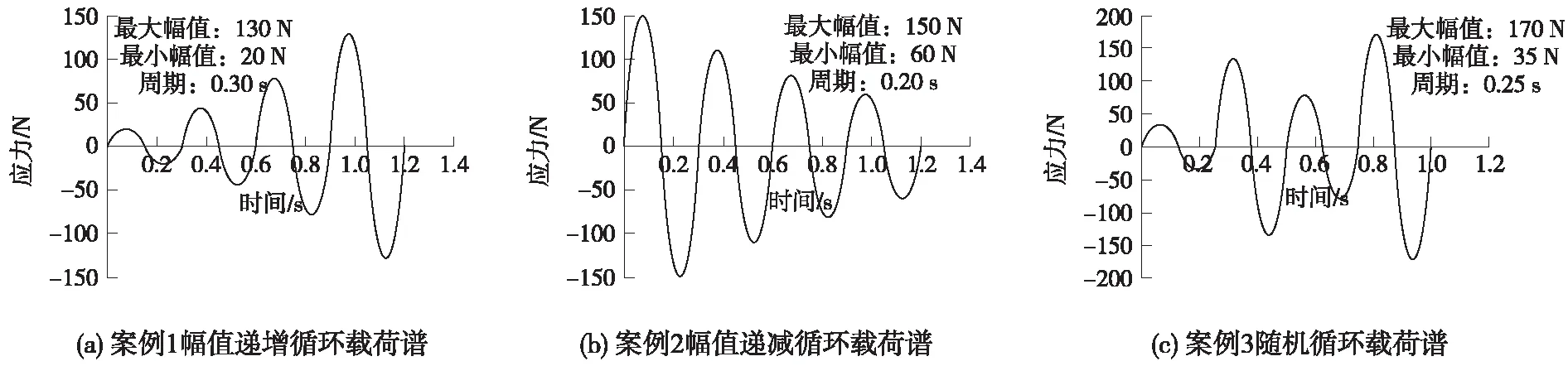
圖10 原始載荷譜

(3)計算原始載荷譜作用于被測試件時的損傷量

ANSYS ncode DesignLife是耐久性分析軟件，利用ANSYS Mechanical的有限元分析(FEA)結果，ANSYS ncode DesigenLife可對實體模型的壽命進行評估計算。其疲勞壽命計算原理是基于線性累積疲勞損傷理論，將一系列應力循環載荷譜帶來的損傷量進行線性的累加，達到計算結構的疲勞壽命。其原理與本文所提出的損傷等效方案一致，故借助于ANSYS ncode DesignLife計算被測試件在不同特征應力循環作用下的疲勞壽命，從而求得各循環的損傷量。

圖11 實心軸承柱疲勞壽命計算分析流

首先，對驗證方案的被測試件，也即實心軸承柱進行有限元分析，并將有限元分析結果導入DesignLife中，其次建立疲勞壽命計算分析流，如圖11所示。最后求出不同特征的應力循環載荷譜下實心軸承柱的疲勞壽命，并根據式(7)求出同特征的應力循環載荷譜的損傷量，典型計算結果如圖12所示。

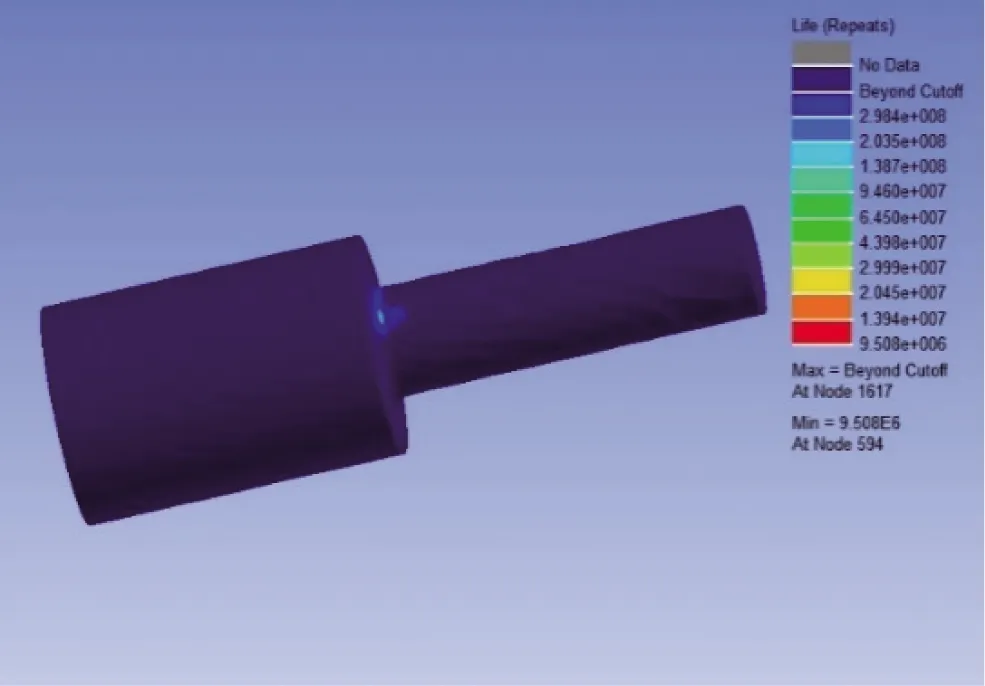
圖12 典型壽命計算結果

圖11所示的壽命計算分析流由有限元計算結果、載荷譜、SN分析計算塊、結果顯示及計算結果數據組成，將Matlab軟件生成的3組不同特征的載荷譜導入至疲勞壽命計算分析流進行計算，得到的計算結果如圖13所示，不同特征載荷譜造成的損傷量統計如表1所示。

表1 不同特征載荷譜損傷量統計

(4)計算等效載荷譜作用于被測試件時的損傷量提取出案例1、案例2、案例3中的最大應力循環周期，分別組成載荷譜，如圖14所示。

將案例1、案例2及案例3等效載荷譜導入至實心軸承柱疲勞壽命計算分析流，分別計算3種案例等效載荷譜作用下實心軸承柱的疲勞壽命，再通過式(7)計算不同案例對應等效載荷譜的損傷量。計算流程如圖11所示，計算結果如圖15及表2所示。

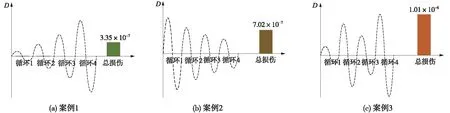
圖13 不同特征載荷譜損傷量計算結果

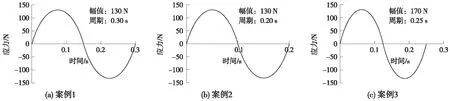
圖14 等效載荷譜

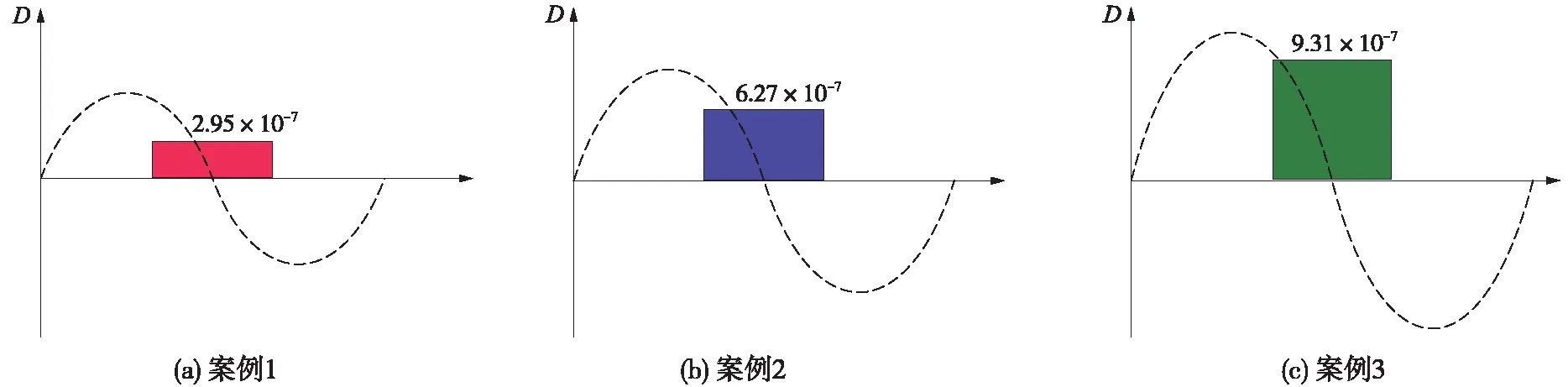
圖15 不同案例對應等效載荷譜損傷量

表2 不同案例對應等效載荷譜損傷量統計

(5)原始載荷譜與等效載荷譜損傷量對比

對比案例1可知，原始載荷譜損傷量為3.35×10-7，等效載荷譜損傷量為2.95×10-7，占比為88.06%；對比案例2可知，原始載荷譜損傷量為7.02×10-7，等效載荷譜損傷量為6.27×10-7，占比為89.32%；對比案例3可知，原始載荷譜損傷量為1.01×10-6，等效載荷譜損傷量為9.31×10-7，占比為92.18%。

通過對比分析得知，以上3種案例的等效載荷譜損傷量在原始載荷譜損傷量中占比在80%～90%，可近似認為等效載荷譜與原始載荷譜對試件造成的損傷量相等。故案例1、案例2及案例3的等效載荷譜損傷量均可認為與其對應的原始載荷譜損傷量相等。

綜上所述，在不考慮加載次序的前提下，本文給出的載荷譜等效方案是有效的。

4 基于損傷等效方案的腕臂型支持裝置疲勞程序譜

前文給出了載荷譜損傷等效方案，并通過具體案例對等效方案進行了驗證，基于此，對剛性接觸網腕臂型支持裝置原始疲勞載荷譜進行等效，最終得到其疲勞程序譜。

本文通過對160 km/h的AC 25 kV剛性接觸網進行弓網動態仿真，得到錨段關節前、后中間區段及錨段關節處定位點的典型振動載荷譜。為增加樣本數量，再次進行弓網動態仿真，獲取以上3個區間多個定位點振動載荷譜。統計不同位置定位點振動載荷譜中最大動應力幅值，如表3所示。

根據前文給出的等效方案，結合表3的統計數據，得到剛性接觸網腕臂型支持裝置的等效疲勞載荷譜。

(1)錨段關節前中間區段

等效載荷譜1應力幅為247.3 N，等效載荷譜2應力幅為287.2 N，等效載荷譜3應力幅為266.7 N，如圖16所示。

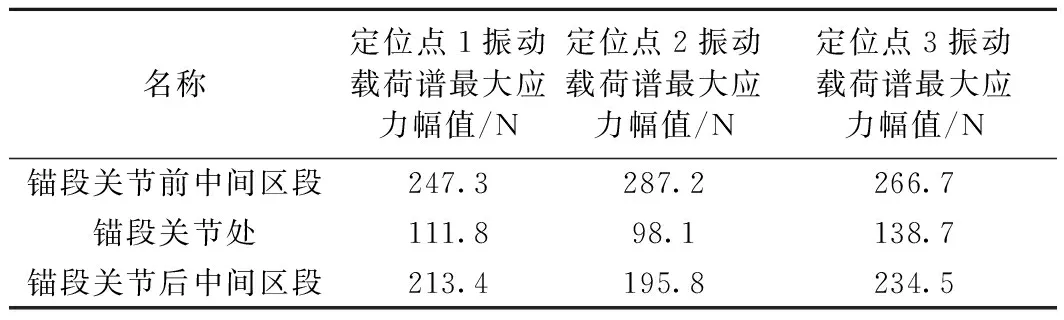
表3 不同位置定位點振動載荷譜最大動應力幅值統計

圖16 關節前區段等效載荷譜

(2)錨段關節處

等效載荷譜1應力幅為111.8 N，等效載荷譜2應力幅為98.1 N，等效載荷譜3應力幅為138.7 N，如圖17所示。

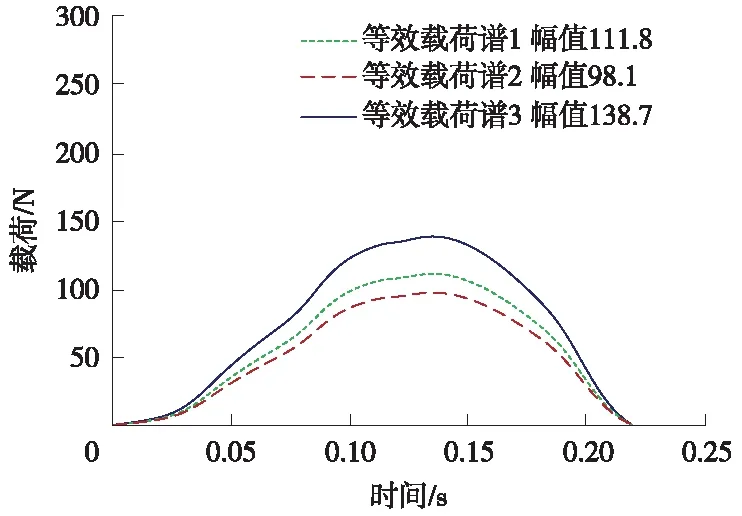
圖17 關節處等效載荷譜

(3)錨段關節后中間區段

等效載荷譜1應力幅為213.4 N，等效載荷譜2應力幅為195.8 N，等效載荷譜3應力幅為234.5 N，如圖18所示。

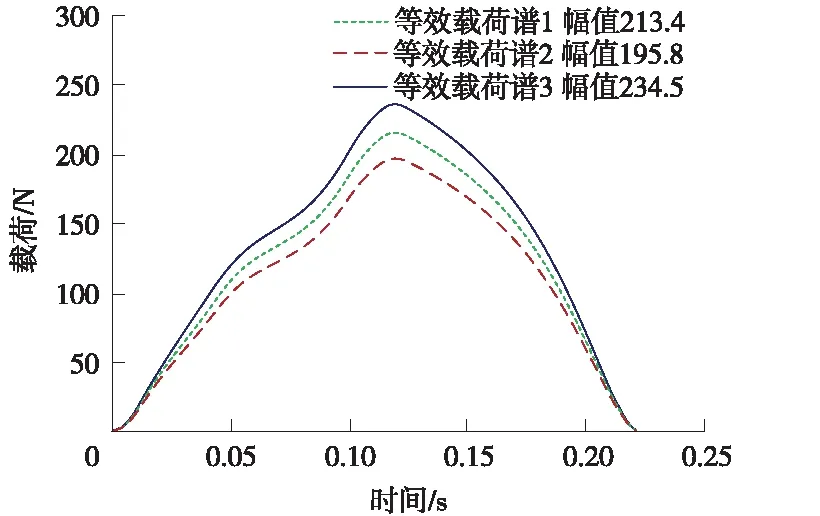
圖18 關節后區段等效載荷譜

160 km/h的AC25 kV剛性接觸網動態仿真得到的定位點振動載荷譜中最大應力作用周期為0.22 s，故圖16、圖17及圖18中均以0.22 s為周期。

至此，完成了剛性接觸網腕臂型支持裝置定位點處疲勞載荷譜的等效，得到的等效載荷譜具有精簡、高效且易實現等特點，滿足疲勞載荷譜的需求。

在剛性接觸網系統中，標稱跨距為6 m，錨段關節處跨距分別為1.8,2,4 m，每個定位點除了承受其自重之外，還承受著相應跨距的匯流排和接觸線的重力，匯流排加接觸線單位長度質量為5.91 kg/m。計算不同跨距長度的匯流排及接觸線重力，將其疊加至表3中得到剛性接觸網腕臂型支持裝置的疲勞程序譜，其幅值統計如表4所示，表中錨段關節處統一以4 m長度計算。

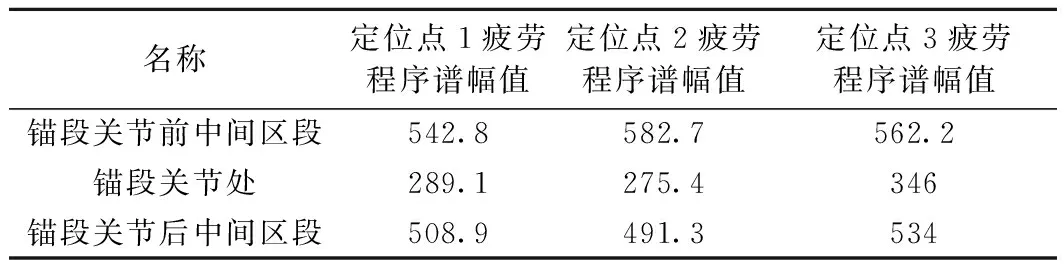
表4 剛性接觸網腕臂型支持裝置的疲勞程序譜幅值 N

5 結論

本文首先介紹了損傷等效理論，在此基礎上，給出了以原始載荷譜中零均值應力最大幅值循環作為原始載荷譜的等效載荷譜的損傷等效方案；其次，通過實際案例對本文給出的載荷譜損傷等效方案進行驗證，驗證結果表明原始載荷譜中最大幅值循環的損傷量與原始載荷譜的總損傷量幾近相等，從而驗證了等效方案的有效性；最后，基于給出的載荷譜等效方案將剛性接觸網腕臂型支持裝置原始載荷譜進行等效，得到AC25kV剛性接觸網腕臂型支持裝置疲勞程序譜。