孕育中的三維水平井修正軌道設計的二次函數法和彈性管柱插連法
李子豐
燕山大學石油工程系
原始水平井設計軌道一般是二維的[1-4],以減少設計難度和施工難度,但在很多情況下也采用三維的[5-8]。無論原始設計是二維的還是三維的,施工過程的修正井眼軌道設計(也稱待鉆井眼軌道設計)都是三維的。三維水平井修正軌道設計的已知參數是當前井底的三維坐標值和井斜角及方位角,入靶點的三維坐標值和井斜角及方位角。由于入靶點的限定條件是入靶點的三維坐標值和井斜角及方位角,并沒有限定井斜角為90°,為此該設計方法適用于一切限定入靶點的三維坐標值和井眼方向的定向井。目前,已有的三維修正水平井軌道設計方法是斜平面圓弧-直線-斜平面圓弧法[9],即雙空間圓弧+直線法。這種設計方法是針對滑動送鉆導向鉆井系統[10-13]提出的。現在,旋轉導向鉆井系統[14-15]應用得越來越多,這種方法設計出來的軌道是否還是最優?有沒有更好的設計方法?為了與旋轉導向鉆井系統的發展相適應,筆者提出了2種三維水平井修正軌道設計方法——二次函數法和彈性管柱插連法,介紹其物理模型、數學模型,以及待解決的問題和潛在價值。
1 現有斜平面圓弧-直線-斜平面圓弧法
圖1描述了三維水平井的井口(坐標原點)、靶區[16]、設計軌道與實鉆軌跡之間的關系。由于滑動送鉆導向鉆井技術先于旋轉送鉆導向鉆井技術出現,并且每趟鉆的導向鉆具上的彎角基本恒定,易于鉆出曲率值基本恒定的井眼,為此,最先出現的三維水平井修正軌道設計方法是斜平面圓弧-直線-斜平面圓弧法[9]。
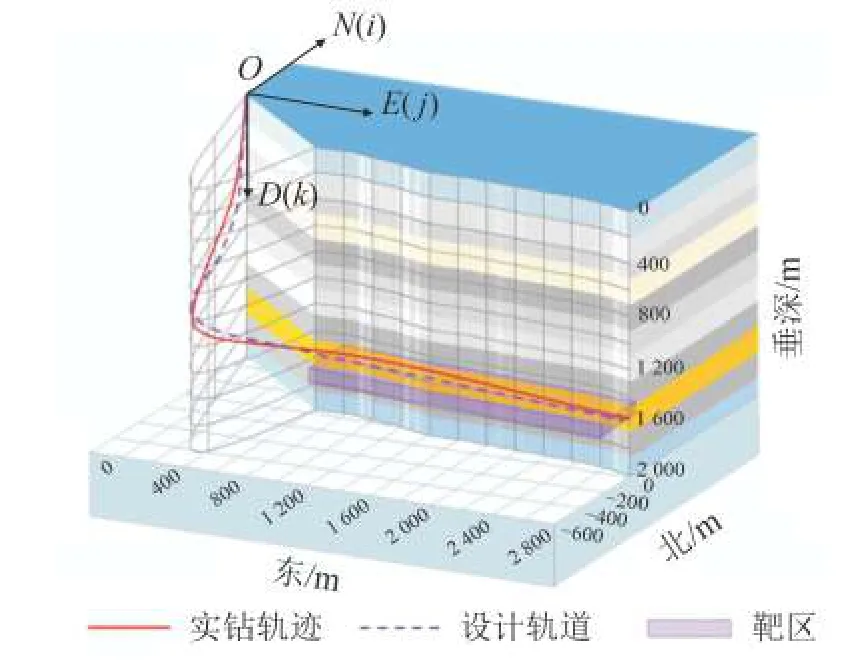
圖1實鉆軌跡與設計軌道和靶區Fig.1 Actual trajectory,designed trajectory and target
1.1 物理模型
該模型可以用圖2所示通過兩個喇叭口的拉線表 示。圖 中,A點 為 當 前 井 底,N1,E1,D1,α1,φ1為A點的北坐標、東坐標、垂深、井斜角和方位角;B點為入靶點,N2,E2,D2,α2,φ2為B點的北坐標、東坐標、垂深、井斜角和方位角;R1為第一圓弧段曲率半徑;R2為第二圓弧段曲率半徑。在A點,以曲率半徑R1對應的圓弧段繞當前井眼軸線旋轉一周,形成一個喇叭口;在B點,以曲率半徑R2對應的圓弧段繞目標段井眼軸線旋轉一周,形成另一個喇叭口;將一無重繩索穿過已鉆井筒和目標井筒及兩個喇叭口后拉直,則繩索形狀即為設計的井眼軌道。
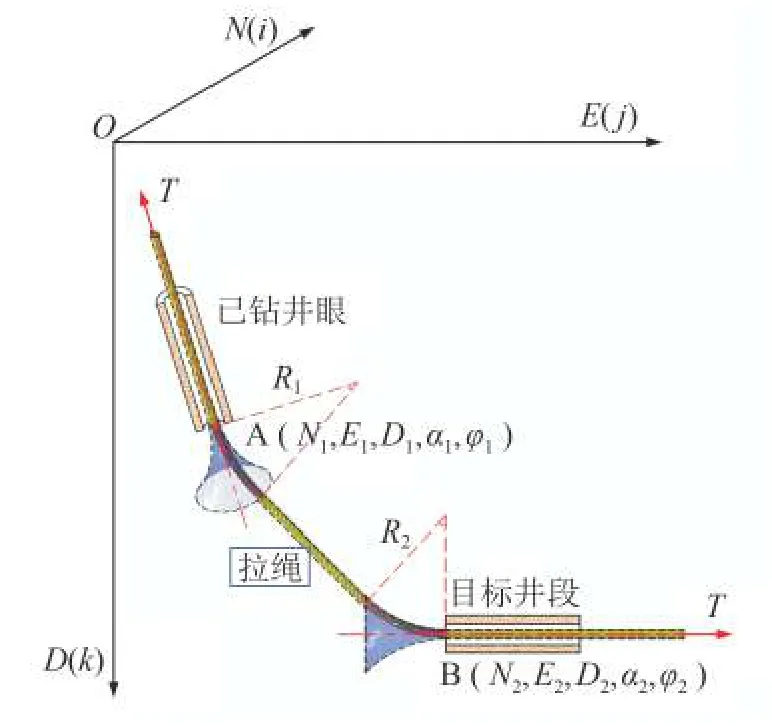
圖2兩個喇叭口-拉繩法物理模型Fig.2 Physical model of two bells-rope method
1.2 數學模型
文獻[9]給出了完整的數學模型及求解方法。
1.3 應用概況
幾乎所有的三維水平井修正軌道設計都在采用該方法。
2 二次函數法
2.1 物理模型
二次函數法中,井斜角和方位角都是A點到修正井眼所在點井眼長度的二次函數,在當前井底和入靶點與井眼軌道相切,如圖3所示。
2.2 數學模型
已知條件為當前井底的三維坐標值、井斜角和方位角,入靶點的三維坐標值、井斜角和方位角。若考慮提前入靶的情況,則將B點沿水平井段軸線左移。
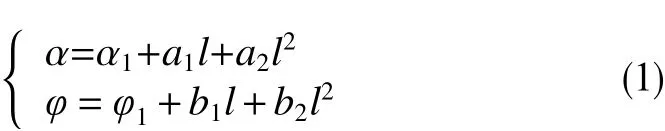
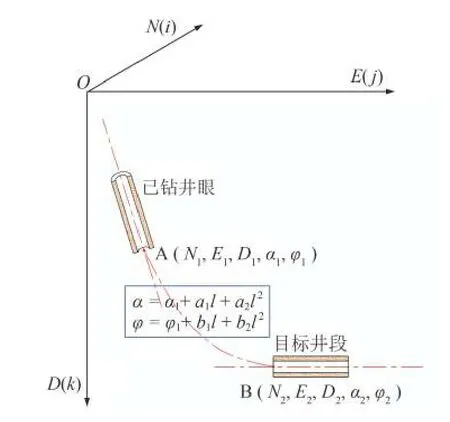
圖3二次函數法物理模型Fig.3 Physical model of quadratic function method
假設式中,α為井斜角,°;φ為方位角,°;l為從A點開始沿井眼軌道到所在點的長度,到達B點時,l=L,m;L為A點到B點的軌道長度,是個未知量;a1,a2,b1,b2為待定系數。共5個未知量,需要5個獨立方程才能確定,上下兩點各有5個參數,恰好可以列出5個獨立方程。
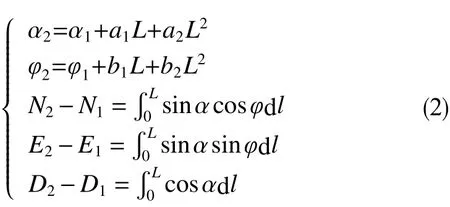
2.3 待解決的問題
求解式(2)中的a1,a2,b1,b2和L。
3 彈性管柱插連法
3.1 物理模型
在該模型中,將彈性鉆柱或套管柱兩端分別插入上端已鉆井筒和目標水平井筒,在管柱兩端加上拉力,當前井底處的拉力為TA,入靶點處的拉力為TB,則管柱中心線即為設計的井眼軌道,如圖4所示。
3.2 數學模型
已知條件:當前井底的三維坐標值、井斜角和方位角,入靶點的三維坐標值、井斜角和方位角。若考慮提前入靶的情況,則將B點沿水平井段軸線左移。
3.2.1 微分方程
如果管柱軸線用r=N(l)i+E(l)j+D(l)k表示,由于彈性管柱處于靜態、沒有扭轉、軸向變形不影響計算結果,油氣井桿管柱動力學基本方程[17-18]簡化為
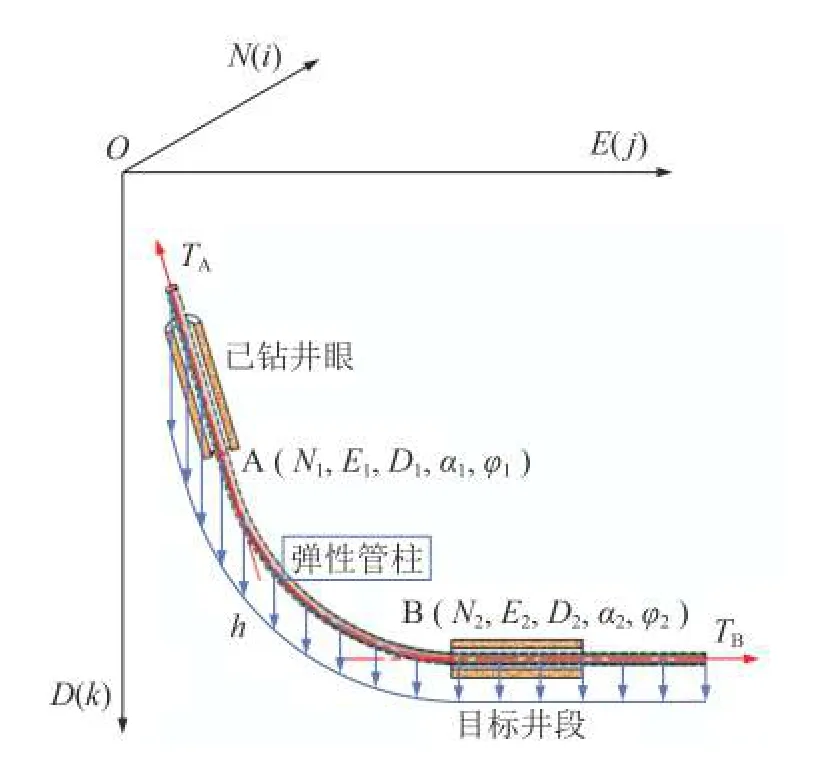
圖4彈性管柱插連法物理模型Fig.4 Physical model of elastic string connection method
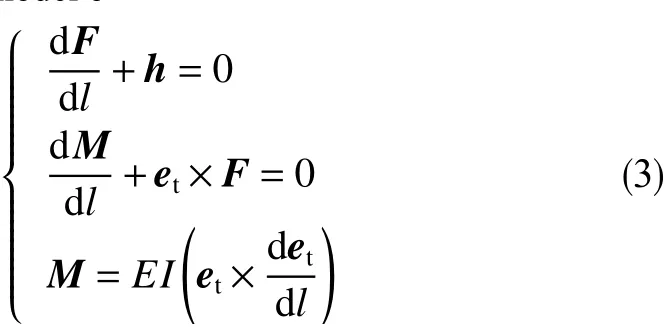
式中,F為管柱的內力,N;h為單位長度管柱上的重力,N/m;M為管柱的內力矩,N·m;E為彈性模量,N/m2;I為截面慣矩,m4;et為管柱變形線的切線方向的單位向量,且

其中
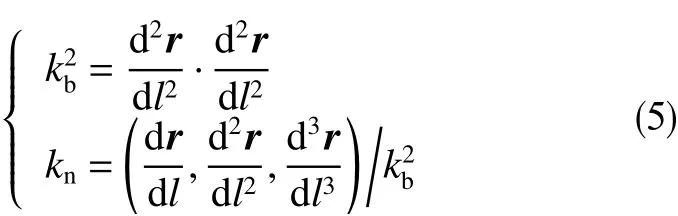
式中,en和eb分別為管柱變形線的主法線方向和副法線方向的單位向量;kb和kn分別為r點的曲率和撓率,m?1。
3.2.2 邊界條件
(1)當前井底。
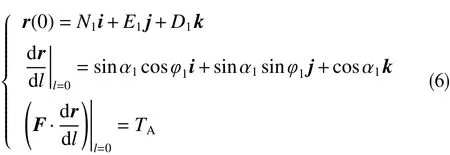
(2)入靶點。
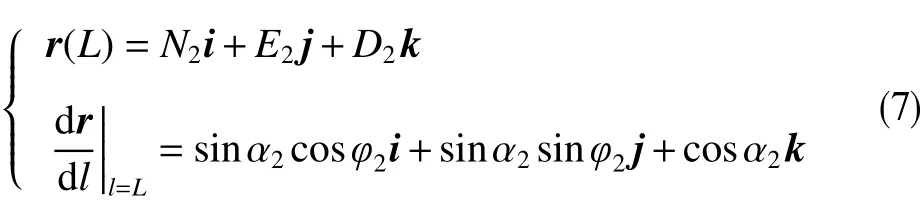
這是一個空間幾何非線性梁問題。
3.3 待解決的問題
求解式(3)~(7)組成的數學模型,得到r=N(l)i+E(l)j+D(l)k的具體數值或表達式。
4 待進行的3種三維水平井修正井眼軌道設計結果的比較
(1)適應鉆進方法的比較。斜平面圓弧-直線-斜平面圓弧法適合滑動幾何導向鉆進;二次函數法和彈性管柱插連法適合旋轉導向鉆進。
(2)設計井段長度的比較。
(3)設計井段施工難度的比較。
(4)設計井段和水平井段施工中,摩阻的比較。理論上,在某一特定條件下,管柱在彈性管柱插連法設計的井筒內,與井壁的接觸壓力全為0,這一點與懸鏈法[19]類似。
5 待進行的實驗驗證
(1)彈性管柱插連法室內實驗。比較理論設計結果與實驗結果。
(2) 3種方法設計結果的現場實鉆驗證及對比。
6 結束語
二次函數法和彈性管柱插連法必將成為新的三維水平井修正軌道設計方法。兩種方法的設計理念和數學模型已經建立,下一步的工作是求解這兩種方法的數學模型、編程和現場應用。

