基于Druck-Prager和MISO模型的混凝土三軸壓縮行為有限元模擬
陳 昊,陳 俊,陳曉鵬(西北有色勘測工程公司,陜西 西安 710054)
0 引言
經過一百余年發展,混凝土已然成為最重要的建筑材料之一,已廣泛應用于工民建、路橋、水利和地下空間開發等工程領域[1,2]。實際工程中,混凝土結構內部多處于三向應力狀態,不同的應力狀態和應力歷史常導致混凝土變形破壞特征呈現顯著差異[3]。早在20世紀20年代,Richart等[4]就開展了混凝土圓柱試樣的三軸受壓試驗。其后,隨著巖石類材料三軸試驗技術不斷發展,高圍壓條件下混凝土常規三軸和真三軸試驗得以開展,尤其在常規三軸試驗方面獲取了極其豐碩的數據,在一定程度上推動了混凝土本構模型的發展和完善[5]。目前,高性能常規三軸試驗機憑借其日益完善的加載和量測技術已成為研究復雜應力狀態和應力路徑作用下混凝土綜合響應行為的主要平臺。如Imran等[5]在20世紀90年代中期采用液壓伺服三軸試驗機研究了不同應力水平條件下,混凝土含水率、孔隙度及應力路徑對其變形破壞特征的影響。該試驗共包含130組三軸試驗,豐富了既有數據庫的試驗結果。本文采用AN?SYS軟件對Imran[5]研究中飽和素混凝土(水灰比為0.4)部分常規三軸壓縮試驗進行有限元模擬,并分析對比Druck-Prager模型及MISO模型(采用Mises強度準則)的模擬結果。此外,在既有三軸壓縮有限元模擬中,模型端部約束條件不盡相同,其主要反映了三軸壓縮試驗中試件端部摩擦力的影響[6,7]。因此,本文進一步基于MISO模型,通過設置模型端部不同的約束條件來模擬試件端部摩擦力無限大和無摩擦約束兩種情況下混凝土壓縮響應特征。
1 研究思路及主要流程
1.1 研究思路
在混凝土非線性有限元分析中,MISO模型和Druck-Prager模型是應用最為廣泛的兩種本構模型,且兩者均與相應的強度準則(為理想塑性模型,屈服強度即破壞強度,故在此不作區分)相匹配。MISO模型遵循Mises強度準則,即材料破壞主要與其屬性和應力偏量第二不變量J2有關,且其應力—應變關系通過多段線性關系給定。Druck-Prager模型將材料視為理想塑性體,材料的塑性破壞由其粘聚力、內摩擦角、剪脹角、J2和應力張量第一不變量I1共同確定,因而在一定程度上可以反映材料在靜水壓力作用下的破壞行為。
本次研究分別基于MISO和Druck-Prager模型模擬文獻[5]中水灰比為0.4的飽和素混凝土三軸壓縮試驗,并綜合對比模擬結果與試驗結果。此外,進一步采用MISO模型對不同端部約束條件的影響進行探究,具體包括:(1)僅約束模型底部環向位移與豎向位移,以模擬壓縮過程中試件端部不存在摩擦力的情況;(2)設置模型底部為固定端,同時約束模型頂部水平方向位移,以模擬壓縮過程中試件端部摩擦力無限大的情況。通過模擬上述兩種極端約束條件,在一定程度上可以反映試件端部摩擦力變化對混凝土三軸壓縮行為的影響。
1.2 混凝土試件有限元模型構建
依據文獻[5],在ANSYS中構建混凝土試件有限元模型,其為圓柱形,高115 mm(z軸方向),直徑54 mm。采用軟件內置的65號實體單元(solid 65)及Concrete材料模擬混凝土,其依據Willam-Warnke(W-W)破壞準則判定混凝土壓碎和開裂[8]。同時,為提升計算效率,加快收斂,本次研究中不考慮混凝土單元的壓碎破壞,但需考慮混凝土壓碎后的應力釋放。混凝土試件幾何模型(見圖1)構建完成后,采用掃略方式對其體網格進行劃分,網格尺寸為3 mm。混凝土試件有限元模型基本信息及材料參數見表1。

圖1 混凝土試件有限元模型
表1中,混凝土試件fc和ν取值與文獻[5]中一致。鑒于文獻[5]中沒有給出混凝土相應的ft,故根據式(1)進行估算[9]。fcb,f1,f2,c,φ由于缺乏試驗數據,故根據混凝土單軸抗壓強度及抗拉強度按式(2)~(8)換算[2]。張開裂縫的剪力傳遞系數及閉合裂縫的剪力傳遞系數根據文獻[2]確定。在此需特別說明,盡管文獻[5]中給出了飽和素混凝土單軸壓縮應力—應變曲線,但相關圖件清晰度有限,無法將實測應力—應變曲線精確定量化,故MISO模型中的應力—應變曲線上升段按Hognestad曲線方程[1](式(9))確定,且將曲線下降段簡化處理為一條水平線,即認為混凝土為理想塑性材料。因此,MISO模型中混凝土E0由fc和ε0確定,其值大于試驗所測E0。而在Druck-Prager模型中,E0作為獨立變量輸入,故可采用實測E0值。

其中:β—混凝土材料常數;σy—混凝土屈服強度(MPa);σc—混凝土應力(MPa);εc—混凝土應變。
1.3 本構模型與邊界條件設置
本次研究采用Druck-Prager模型及MISO模型進行模擬,并綜合對比其模擬結果。MISO模型將應力—應變曲線劃分為多個線性段。如§2.2所述,各線性段的應力—應變關系由Hognestad曲線方程確定。在Druck-Prager模型中,應力—應變關系通過給定的材料常數即可確定,其規定在屈服強度之前服從線彈性應力—應變關系,屈服強度之后則為理想塑性。

表1 混凝土試件有限元模型基本信息及材料參數
模擬過程中,首先采用應力邊界條件在模型側表面施加擬定圍壓(分別為0,25.5和51.2 MPa),待求解平衡后,在模型頂部施加位移邊界條件(沿z軸負方向位移為1~10 mm)以模擬壓縮加載。此外,模型頂面及底面約束條件詳見表2。
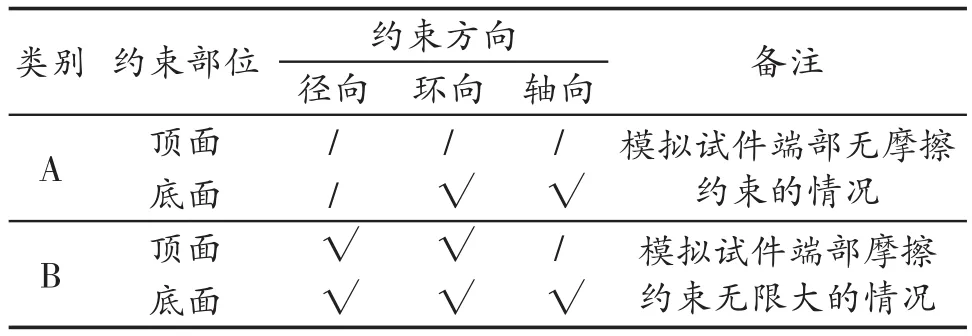
表2 混凝土試件有限元模型頂面及底面約束條件
1.4 模擬結果后處理
本次研究主要對模型軸向應變、體應變及軸向應力間的關系展開分析,并與Imran的研究結果進行對比。其中,模型體應變和軸向應變可采用AN?SYS內置后處理模塊進行提取。但由于模擬中采用位移邊界條件進行軸向加載,故采用命令流提取模型頂面各節點反力的合力,并將該合力與模型頂面面積之比作為所施加的軸向應力(σa)。
此外,鑒于文獻[5]中采用電阻式應變片量測混凝土柱中間部位的表面應變,故本次研究亦提取混凝土試件有限元模型中間部位單元的側向應變,并采用與文獻[5]相同的計算方式(式(10))求取體應變。

式中:εV—體應變;εa—軸向應變;εL—側向應變。本次研究中規定以拉伸為正、壓縮為負。相應地,試件體積膨脹(剪脹)為正,試件體積縮小(剪縮)為負。
2 結果分析
2.1 不同本構模型模擬結果對比分析
本節模擬均采用A類約束條件(不考慮端部摩擦),基于Druck-Prager模型和MISO模型得到的σaεa曲線與εV-εa曲線分別如圖2和圖3所示。結果表明模擬結果與試驗結果總體變化趨勢基本一致,但在具體數值上存在較大偏差。表3列出了各圍壓條件下混凝土試件峰值強度σpeak以及峰值強度對應的軸向應變εpeak與割線模量Es的實測值和模擬值。
就峰值強度而言,無側限條件下兩種模型模擬結果與實測結果較為接近。當圍壓增大,兩種模型的模擬結果均偏離試驗結果。其中,MISO模型模擬出的應力—應變關系較為保守。相反,Druck-Prag?er模型則嚴重高估了混凝土試件抗壓強度,其在51.2 MPa圍壓條件下的抗壓強度模擬值高達983.09 MPa。Druck-Prager模型的強度準則考慮了靜水壓力作用,且認為混凝土破壞之前處于線彈性狀態,其或許是導致試件在高圍壓條件下模擬抗壓強度顯著提升的原因。此外,εpeak的實測值和模擬值均隨圍壓增大而減小,反映出圍壓對混凝土變形的約束作用,即隨圍壓增大,混凝土延性增強。然而,MISO模型所得εpeak值隨圍壓變化并不顯著,其與試驗結果差異較大。同時,Es的模擬值普遍比實測值大,且兩者隨圍壓變化規律相反,即Es實測值衰減幅度較大。其原因在于本文采用的MISO模型和Druck-Prager模型均為理想塑性模型,且應力—應變曲線上升段斜率變化較小,所以無法反映出混凝土彈性模量的快速衰減。在此亦需強調,由于模擬采用的本構模型不含下降段,故模擬結果無法反映混凝土的應變軟化行為。
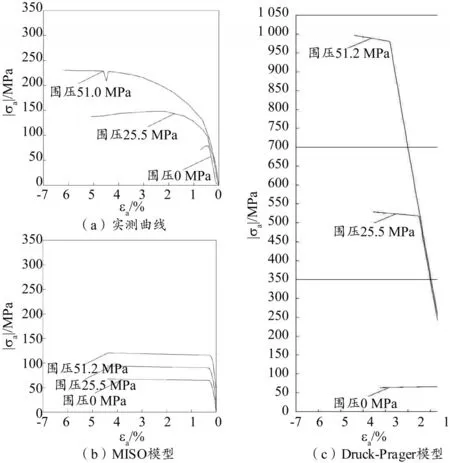
圖2 軸向應力σa與軸向應變εa關系曲線

圖3 體應變εV與軸向應變εa關系曲線

表3 混凝土試件峰值強度、峰值強度對應的軸向應變與割線模量模擬值和實測值
就體應變—軸向應變關系而言,Druck-Prager模型的模擬結果顯著優于MISO模型。相較實測曲線,Druck-Prager模型模擬結果夸大了混凝土剪縮程度,高估了裂縫產生時的軸向應變,該現象在低圍壓條件下尤為顯著[圖3(c)中加粗線段為趨勢延長線,并非模擬結果]。MISO的模擬結果則與實際相悖:(1)一方面,隨圍壓增大,混凝土模型剪縮程度減小;(2)另一方面,模型剪縮程度對圍壓改變極不敏感,且體變值極小,表明壓縮未導致混凝土內部裂隙顯著發育。MISO模型模擬結果與試驗結果的差異可能與模型端部約束條件有關,即三軸試驗中混凝土試件端部與加壓板之間存在摩擦力,其會顯著影響混凝土變形破壞特征,故擬基于MISO模型對端部約束條件影響進行探究。同時,鑒于Druck-Prager模型嚴重高估混凝土強度,并兼顧計算效率,在此不再基于Druck-Prager模型分析端部約束條件影響。
2.2 不同端部約束條件模擬結果對比分析
在前文基礎上,本節采用B類約束條件(端部摩擦無限大)進行模擬,最終得到的σa-εa曲線與εV-εa曲線如圖4和5所示。
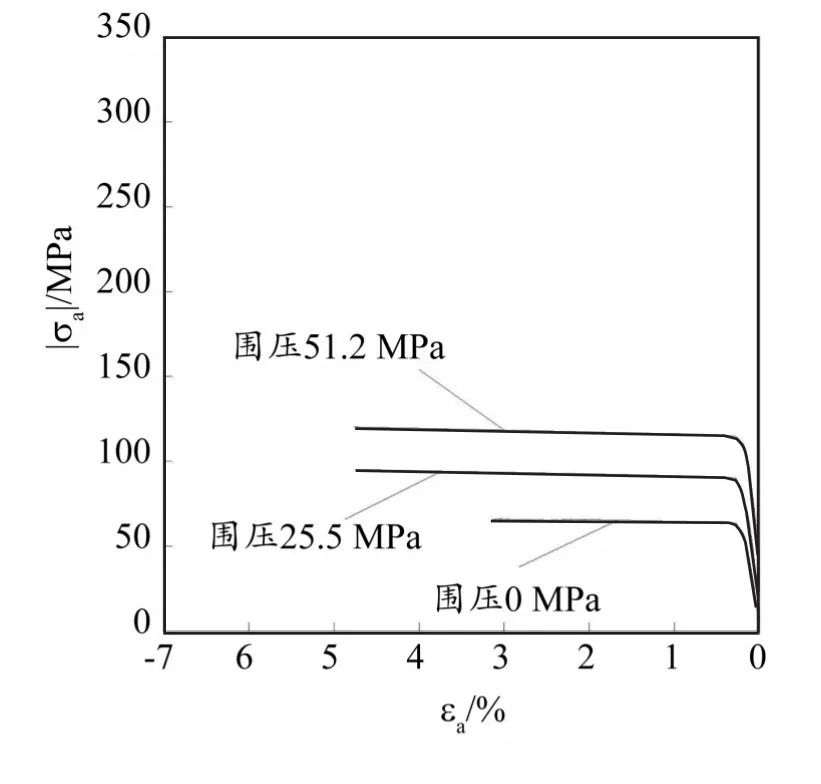
圖4 B類約束條件下軸向應力σa與軸向應變εa關系曲線

圖5 B類約束條件下體應變εV與軸向應變εa關系曲線
圖4和5表明,端部約束條件對混凝土應力—應變曲線無顯著影響,但會改變混凝土體變特征。相較圖3(b),當約束模型端部水平位移時,混凝土發生明顯的剪脹,即端部摩擦約束加劇混凝土內部結構損傷。然而,與實測混凝土體變特征相比,B類約束條件下MISO模型的模擬結果仍有較大缺陷,包括:(1)混凝土在壓縮初始階段的剪縮效應未能體現;(2)體變響應對圍壓的敏感性仍未能凸顯。
3 結論
(1)MISO和Druck-Prager模型的模擬結果與試驗結果總體變化趨勢基本一致,尤其在無側限條件下,Druck-Prager模型模擬結果與實際更為貼近。
(2)施加圍壓時,模擬結果與試驗結果在具體數值上存在較大偏差。其中,MISO模型所得抗壓強度較保守,而Druck-Prager模型極大地高估了混凝土抗壓強度。例如,當圍壓為51.2 MPa時,Druck-Prager模型所得抗壓強度高達983.09 MPa。
(3)就MISO模型而言,端部摩擦約束對混凝土應力—應變曲線無顯著影響,但會改變混凝土體變響應特征,加劇混凝土內部結構損傷。

