基于狀態空間法的軌道不平順與車體橫向加速度關聯模型

牛留斌,劉金朝,曲建軍,尹 峰

(中國鐵道科學研究院集團有限公司 基礎設施檢測研究所，北京 100081)

軌道不平順是引起車輛振動的主要來源，軌道的平順性好壞直接影響車輛高速運行平穩性和舒適性。車體振動加速度是衡量車體振動程度的量度，是軌道不平順輸入特征及車輛動力學響應特性的綜合反映。兩者之間關聯的研究有助于深入理解車輛的傳遞特性、找出車輛敏感波長、避免車輛振動加劇。同時，結合車輛振動和軌道不平順綜合評價軌道質量狀態，有利于全面分析軌道病害，科學指導工務養護維修。因此，國內外對軌道不平順與車體振動之間關聯展開了大量的研究。文獻[1-2]采用傳遞函數或短時傅里葉變換小波分析技術研究軌道不平順與車輛振動響應信號之間關聯；文獻[3-4]通過車輛-軌道耦合動力學理論及頻率分析方法研究軌道不平順與車體振動之間的傳遞特性。以上研究多是采用信號處理方法(如相干分析等)或車輛-軌道動力學理論借助頻譜分析研究軌道不平順與車體振動加速度之間的關聯，側重于找出引起車體強烈振動的單項軌道不平順敏感波長定量分布，不能給出軌道不平順與車體振動之間的顯式傳遞特性。車體振動是由軌道不平順引起的綜合響應，在近似的情況下，單項軌道不平順引起的車體振動起到主要因素，如文獻[5]利用系統辨識方法建立ARX模型研究軌道長波高低不平順與車體垂向加速度之間傳遞關系。但相對于軌道長波高低不平順和車體垂向加速度之間近似線性的傳遞關系，軌道不平順與經過車輛一、二系懸掛傳遞后的車體橫向加速度之間存在著較為復雜的非線性傳遞特性，單項軌道不平順對車體橫向加速度的影響隨著頻段而不同，這使得兩者的傳遞關系更為復雜，文獻[5]中的ARX模型不能有效地表征兩者之間的傳遞關系。

本文基于系統辨識理論，以我國某列高速綜合檢測列車在某高速鐵路上的實測軌道不平順及車體橫向加速度數據為基礎，采用多輸入單輸出狀態空間(State-space)模型建立軌道不平順與車體橫向加速度之間的關聯模型研究兩者之間的傳遞關系。利用狀態空間模型的傳遞函數及實測軌道不平順對車體橫向加速度進行預測，并與文獻[5]中ARX模型預測車體加速度結果進行了對比。

1 關聯模型構建

本文構建的軌道不平順與車體橫向加速度之間的狀態空間模型是系統辨識理論中的方法之一，是在不使用系統結構本身固有參數和內部復雜傳遞關系的基礎上，通過實測得到的輸入輸出數據來辨識系統的傳遞特性。首先利用相干分析法找出不同頻段上軌道不平順與車體橫向加速度之間的相干特性，為不同頻段的狀態空間模型選擇合適的輸入輸出波長；再根據高速綜合檢測列車實測數據選擇關聯模型的合理階數及相應的模型參數；最后利用殘差及相關系數對關聯模型進行驗證。

1.1 分頻段方法

車體橫向加速度是由不同類型的軌道不平順引起的，同一類型的軌道不平順的不同波長成分將影響著車體橫向加速度的不同頻段[6]。為了簡化模型輸入變量，在軌道不平順有效測試波長范圍內，根據軌道不平順與車體橫向加速度之間的相干特性找出不同頻段上與車體橫向加速度相干較強的模型輸入，將狀態空間傳遞模型分為低頻和中高頻兩個頻段。相干函數[7]能夠表征模型輸入與輸出之間的相干特性，可以反映軌道不平順u和車體橫向加速度y之間的在不同頻段上的依賴程度。相干函數Cuy為

( 1 )

式中：ω為空間頻率，m-1；Guy(ω)是軌道不平順輸入u和車體橫向加速度輸出y的互功率譜，mm·m2/s2；Guu(ω)為模型輸入軌道不平順u的自功率譜，mm2·m；Gyy(ω)為模型輸出車體橫向加速度y的自功率譜，m3/s4。自功率譜及互功率譜的分析方法參考文獻[7]。本文采用平均周期圖譜法(Welch韋爾奇)進行功率譜計算，段內傅里葉變換點數是4 096，加漢明窗(Hamming)，段與段間數據樣本重疊50%。

相干函數的取值范圍在0～1.00之間，相干函數值越接近1.00，說明模型輸入與輸出之間的依賴性越強。通常認為相干函數值大于0.80時，輸出與輸入之間存在有較強的相干關系。

1.2 狀態空間模型

在狀態空間模型中，軌道不平順輸入u和車體橫向加速度輸出y之間的關系表述[8-9]為

( 2 )

式中：u(t)為t時刻的軌道不平順輸入，mm；y(t)為t時刻車體橫向加速度輸出，m/s2；x(t)為狀態空間模型的狀態變量；v1(t)和v2(t)為t時刻模型誤差值；A、B、C、D為狀態模型待估參數。在本文中通過子空間算法得到模型待估參數，假定空間狀態模型的階數n、模型輸入輸出的個數分別為m和r，則參數矩陣A為n×n矩陣、B為n×m矩陣、C為r×n矩陣、D為r×m矩陣。

空間狀態模型輸入u和輸出y之間的傳遞函數為

G(ω)=C(ωIn-A)-1B+D

( 3 )

式中：In為n階單位矩陣。

由實測數據訓練模型參數A、B、C、D，根據式(3)得到模型傳遞函數，再由模型傳遞函數及實測軌道不平順數據預測相應的輸出，公式為

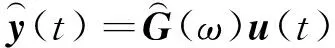
( 4 )

1.3 模型參數優化方法

狀態空間模型參數A、B、C、D是通過實測軌道不平順數據與車體橫向加速度數據訓練估計得到的，選擇合理的模型階數有利于優化模型參數的數量，提高系統辨識精度，減少模型誤差。

定義模型的損失函數V為

( 5 )

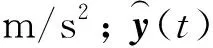
由式(5)可知，損失函數是待估參數A、B、C、D的函數，最優化預測模型的合理階數n應使模型損失函數V最小。獲得模型最小損失函數的判別方法有FPE(Final Prediction Error)準則或AIC(Akaike Information Criterion)準則[8]，其表達式分別為

( 6 )

( 7 )

式中：ΔFPE和ΔAIC分別為FPE準則和AIC準則計算出的最小誤差值；d為模型中待估參數個數；N為估計模型參數所使用的實測數據樣本個數；V為由式( 5 )定義的模型損失函數。

通過FPE準則或AIC準則，可以得到合理階數的狀態空間模型及對應的模型參數。

1.4 模型精度驗證

為了確保所構建的狀態空間模型能夠應用于實際預測并保持較高的預測精度，一般采用模型預測與實測數據之間的殘差及相關系數來檢驗狀態空間模型的精度。

( 8 )

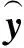
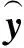
( 9 )

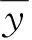
相關系數ρ的絕對值為0～1.00；當相關系數ρ的絕對值大于0.80時，認為兩組數據之間具有較強的線性相關性。

2 數值試驗

車體橫向振動不但與軌道不平順有關，還與車輛系統的動力性能、車輪踏面圓順度等因素有關，所建立模型反應了軌道不平順與車體橫向加速度之間的傳遞關系。由于不同的檢測車輛在動力性能上的差異，利用不同檢測車輛上的實測數據建立模型時得到的傳遞函數會有差異。

車輪踏面圓順度會引起車輛周期性振動，基波的波長與車輪輪徑有關，不大于3 m，在建構模型時會將該波長成分濾除。車輪圓順度引起的二階及以上諧波成分在總成分中的比例很少，對模型的建構沒有影響。

本文中軌向不平順是指實測左右兩側軌向不平順的平均值；由于軌道短波不平順引起激振頻率高，對車體振動加速度影響不大，因此忽略3 m以下軌道不平順對車輛橫向加速度的影響，主要考慮中長波范圍軌道不平順與車體振動之間的關系，所以在數據使用前首先對實測車體橫向加速度數據進行了空間頻率為0.35 m-1的低通濾波，保留了大于3 m的波長成分，軌道檢測數據的采樣間隔為0.25 m，車輛檢測速度為200 km/h。

利用構建模型的傳遞函數及實測軌道不平順數據對車體橫向加速度進行預測，結果與實測數據的相關性對比是驗證模型辨識精度的方法。所以將實測數據分為兩個相互獨立的部分：一部分用于辨識訓練關聯模型的參數，樣本數N為10 000組；另一部分軌道不平順數據及關聯模型用于預測車體橫向加速度，并與實測車體加速度數據進行對比。

2.1 狀態空間模型分頻段相干函數

高速綜合檢測列車實測車體橫向加速度功率譜曲線和車體橫向加速度與長波軌向不平順、曲率、超高、水平等的相干函數曲線，見圖1。由圖1可知，車體橫向加速度在空間頻域上的能量分布比較集中，主要分布在空間頻域0.010～0.050 m-1范圍內。在低于0.005 m-1的頻段時，車體橫向加速度與超高及曲率相干函數值大于0.80；在0.005～0.008 m-1頻段時，車體橫向加速度與水平相干函數值較大；在0.008～0.35 m-1頻段，車體橫向加速度與長波軌向不平順相干函數值較大。

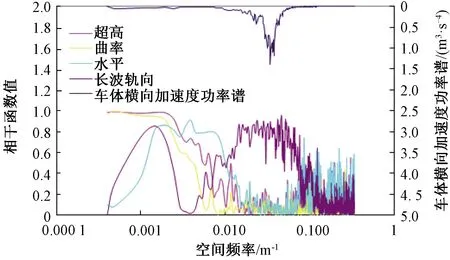
圖1 高速綜合檢測列車車體橫向加速度功率譜及相干函數

在不同的頻段，不同類型的軌道不平順與車體橫向加速度的相干特性是不一樣的。分為不同的頻段有助于建立不同類型軌道不平順與車體橫向加速度之間的狀態空間模型。由圖1可知，本文分別在小于0.005 m-1頻段和0.005～0.350 m-1頻段，在低頻區段，狀態空間模型的輸入為曲率和超高；中高頻區段，狀態空間模型的輸入為長波軌向和水平。低頻模型是對實測數據0.005 m-1低通濾波得到的；中高頻數據是對實測數據頻率為0.005～0.350 m-1帶通濾波得到的。

2.2 低頻狀態空間模型

由式(7)AIC準則公式計算值與狀態空間低頻車體橫向加速度關聯模型階數n之間的曲線見圖2，圖2中當模型的階數n選為6時，對應的模型AIC準則值最小。所以，在建立中高頻橫向加速度與軌道不平順之間的狀態空間關聯模型時，選用的階數n為6，所建模型的傳遞函數特性曲線見圖3，幅頻特性曲線變化平緩，相頻特性曲線顯示兩者沒有相位差。

圖2 狀態空間模型AIC與階數關系圖(低頻)

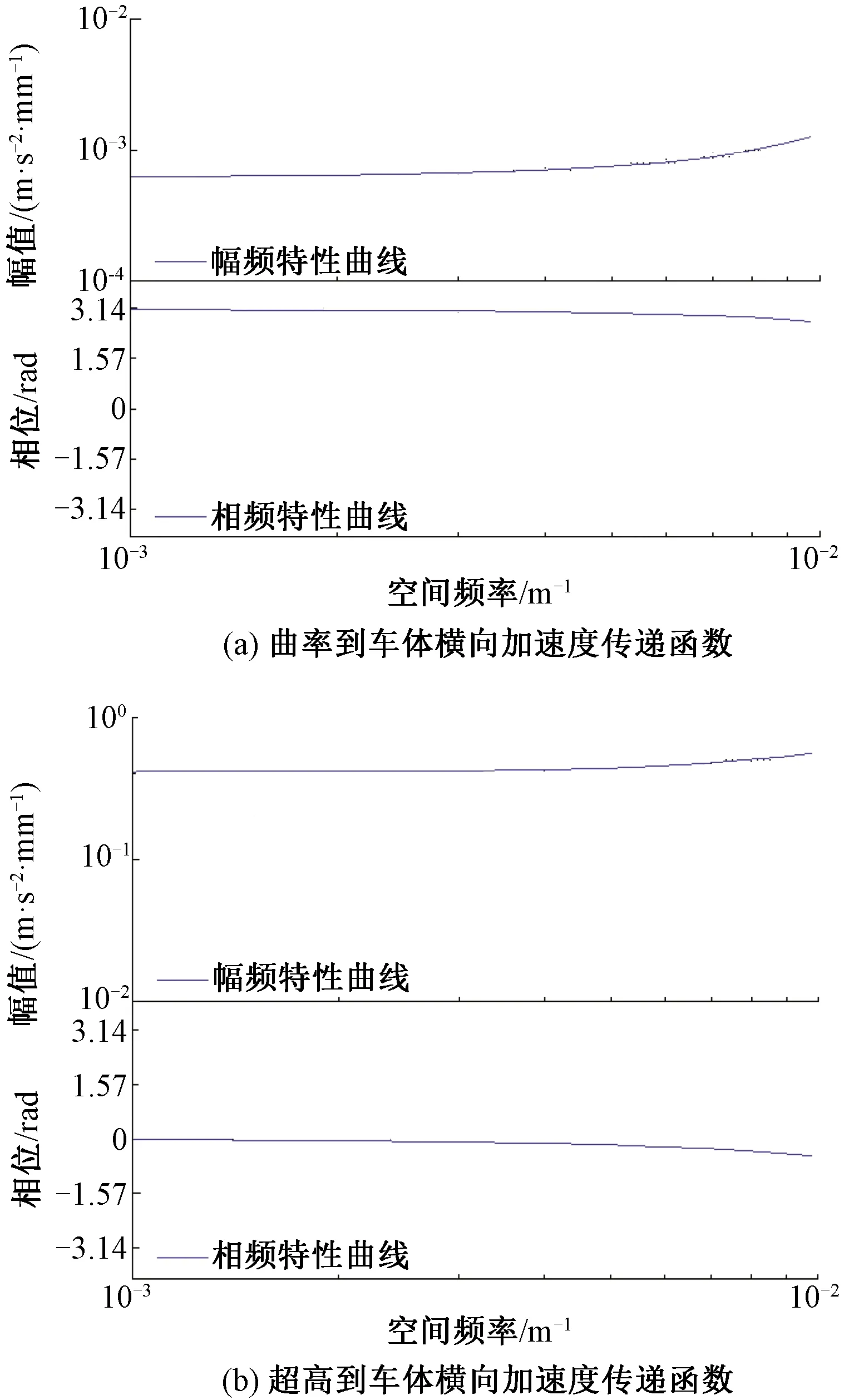
圖3 狀態空間法傳遞函數特性(低頻模型)

利用狀態空間模型傳遞函數及實測曲率、超高數據預測的車體橫向加速度與實測加速度的對比圖見圖4。圖4中顯示了直線及曲線線況條件兩者波形吻合良好，其相關系數為0.98，直線部分的對比見圖5。

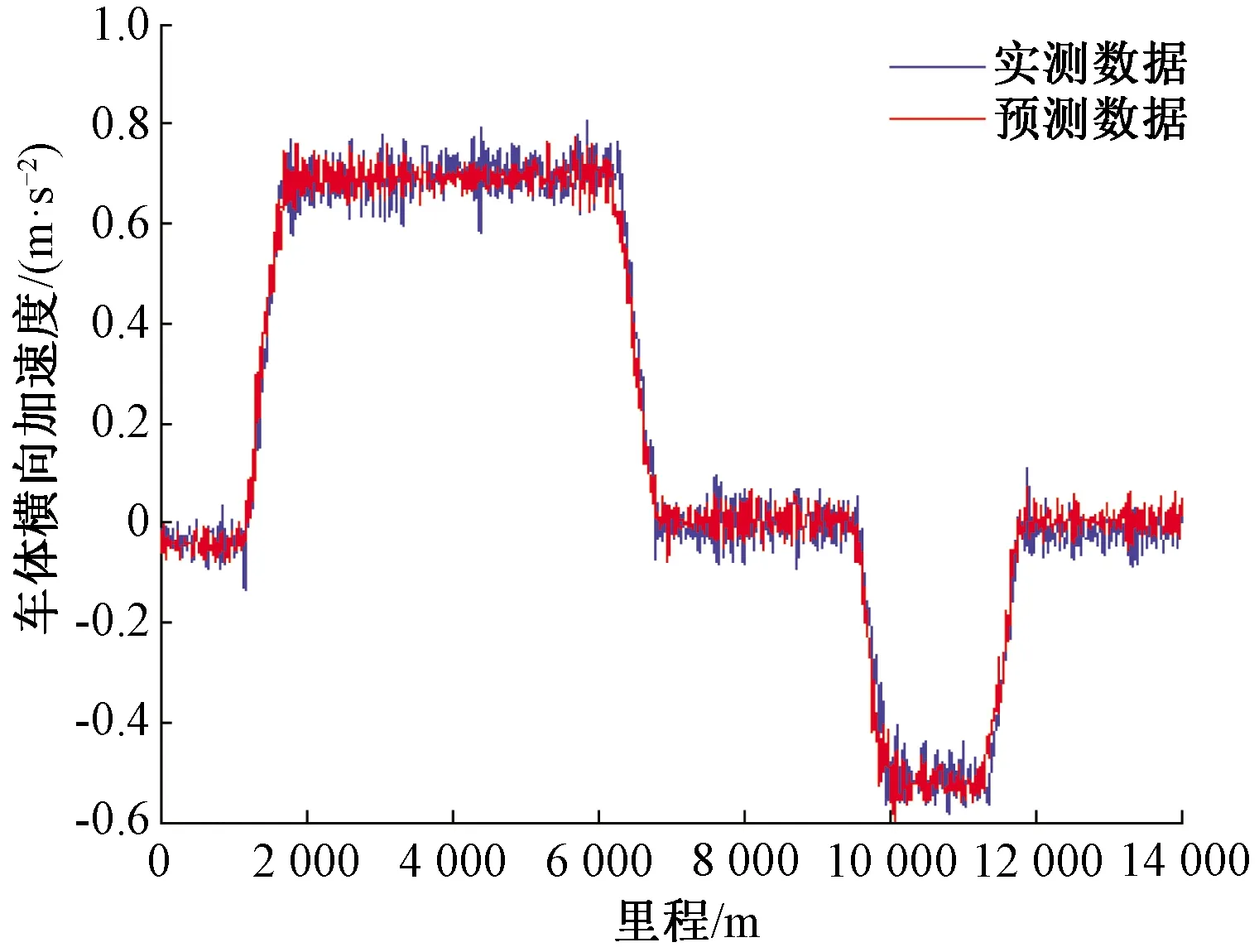
圖4 狀態空間法預測低頻車體橫向加速度及對比

圖5 狀態空間法預測低頻車體橫向加速度及對比(直線區段)

兩者的殘差re服從正態分布N(-0.001 3，0.004 6)，近似滿足0均值假設，其正態概率分布曲線見圖6。

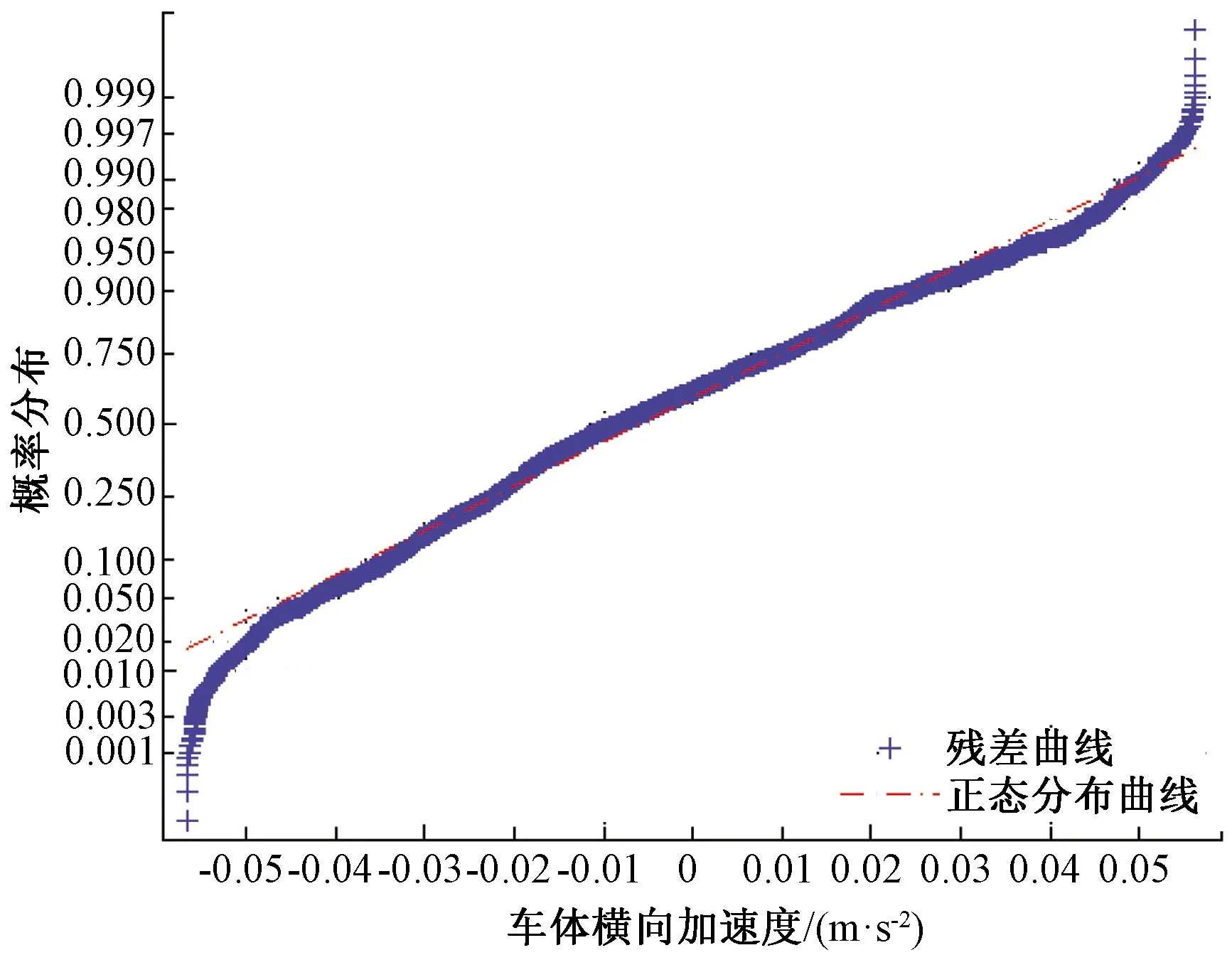
圖6 狀態空間模型殘差分布圖

2.3 中高頻狀態空間模型

中高頻狀態空間模型的階數是通過AIC準則進行優化定階的，按式(7)AIC準則公式計算值與狀態空間模型階數n之間的關系曲線見圖7，圖7中曲線表明，當狀態空間模型的階數n選為6時，對應的模型AIC準則值最小，模型最合理。所以，在建立中高頻橫向加速度與軌道不平順之間的狀態空間模型時，選用的階數n為6。

在0.005～0.350 m-1頻段利用狀態空間法建立長波軌向不平順、水平與車體橫向加速度之間的多輸入單輸出(MISO)關聯模型，由式(2)得到模型輸入與輸出之間的傳遞函數幅頻特性與相頻曲線見圖8，兩者的相頻特性曲線上在0.047、0.062、0.21 m-1處出現了相位由-π到π的突變，在利用模型傳遞函數預測輸出時將造成該頻段預測數據的不準確。

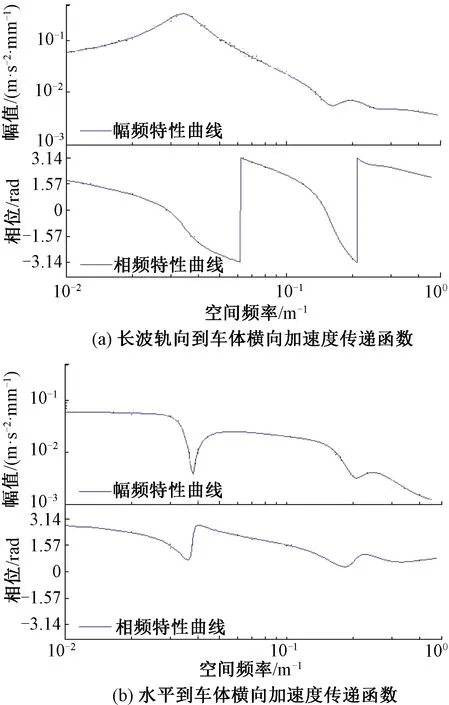
圖8 狀態空間法傳遞函數特性(中高頻)

利用6階狀態空間模型傳遞函數及實測軌道長波軌向、水平預測到的車體橫向加速度，并與實測車體橫向加速度進行了對比，見圖9，兩者的相關系數為0.85，兩者的殘差服從正態分布N(0.000 3，0.006 3)，滿足殘差近似0均值假設，方差0.006 3反映了模型殘差偏離零均值的程度較小，模型輸出值與實測值很接近。殘差正態概率分布曲線見圖10。

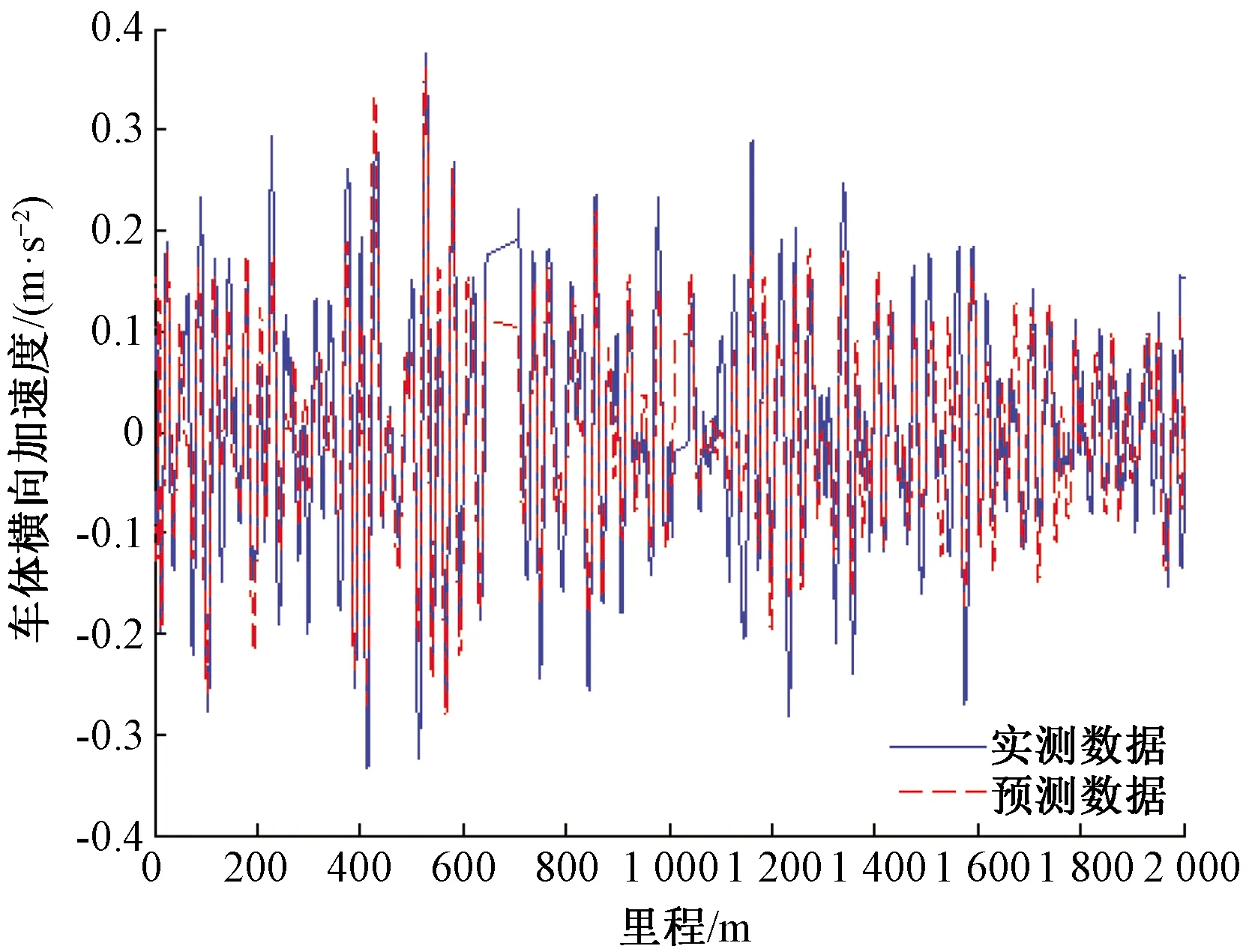
圖9 中高頻橫向加速度預測結果圖(圓曲線部分)

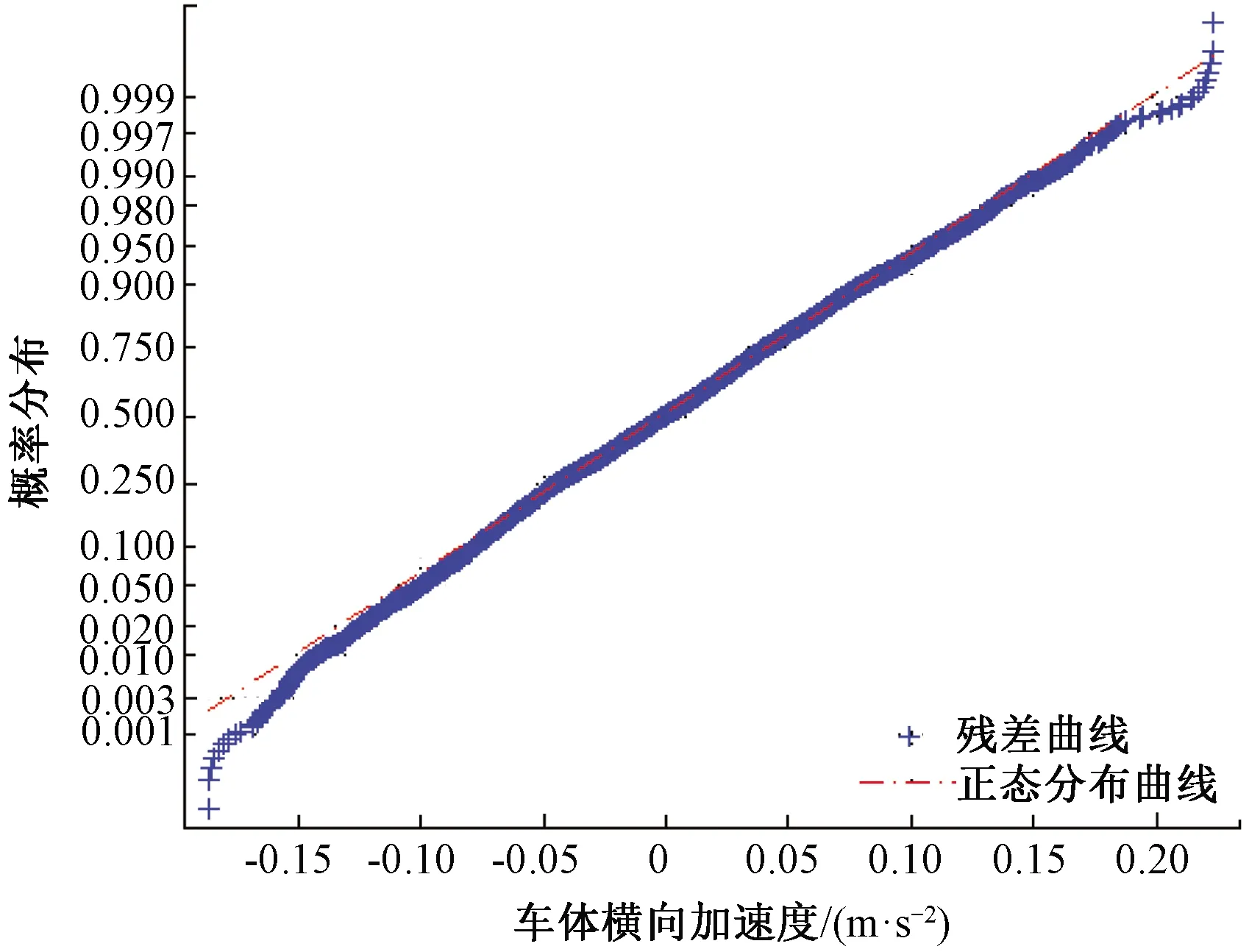
圖10 中高頻殘差分布曲線

利用n階狀態空間模型預測車體橫向加速度時，前n個初始值設置為0，在開始預測第n+1個值時，存在較大的誤差，經過20至40步的迭代計算，預測車體橫向加速度數據將逐漸收斂于實測波形。

除了在個別高頻數據外，利用空間狀態模型預測的車體橫向加速度與實測車體橫向加速度吻合良好，兩者之間的相關系數較高，存在著較強的線性相關性。

傳遞函數能夠反映狀態空間模型能夠辨識軌道不平順與車體橫向加速度之間關聯關系的準確性，而傳遞函數的正確性可以通過實測數據進行驗證。

3 模型驗證及對比

利用實測軌道檢測數據及狀態空間關聯模型傳遞函數預測車體橫向加速度，并與相應的實測車體橫向加速度結果進行對比。利用ARX模型建立軌道不平順與車體橫向加速度關聯模型的方法可參考文獻[5]。圖11、圖12分別利用狀態空間模型傳遞函數、ARX模型傳遞函數并與相應的實測車體橫向加速度進行對比。圖11、圖12中所選用的樣本數據區段長度為1 500 m，曲線半徑為12 000 m，共有6 000個樣本點。

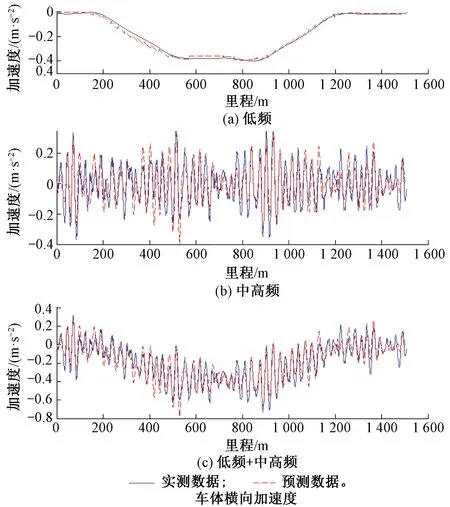
圖11 狀態空間模型預測車體橫向加速度數據與實測數據對比圖

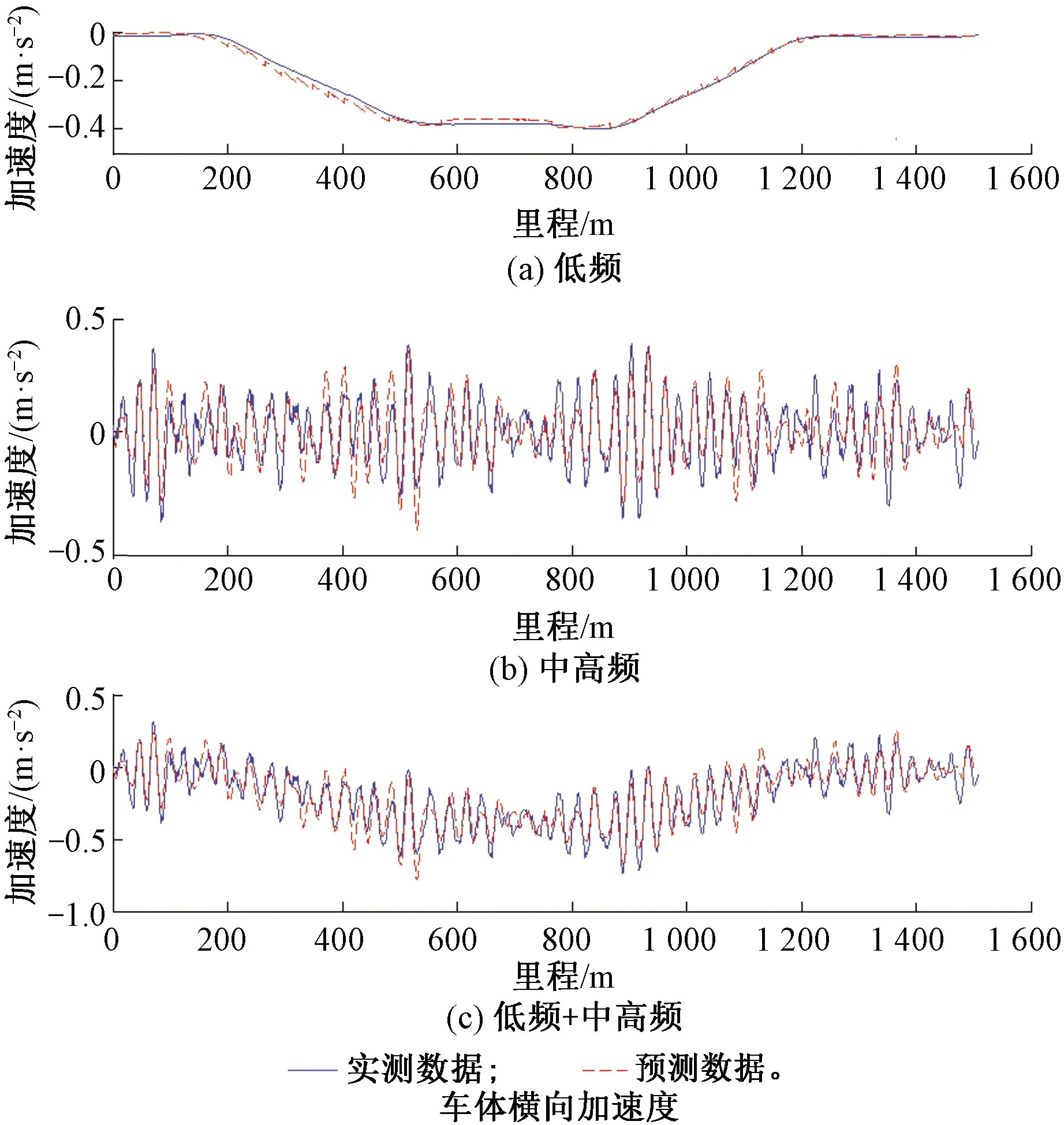
圖12 ARX模型預測車體橫向加速度數據與實測數據對比圖

由圖12可知，無論線型是直線或者曲線，狀態空間模型及ARX模型預測的車體橫向加速度波形與實測波形吻合一致，但狀態空間模型預測的低頻、中高頻及整體數據與實測數據的相關系數分別為0.97、0.86、0.94，而ARX模型的相關系數分別為0.86、0.80、0.82。

由上述利用關聯模型傳遞函數預測車體橫向加速度結果與實測車體橫向加速度數據對比可知狀態空間模型能夠較準確的辨識軌道不平順與車體橫向加速度之間的傳遞關系，而ARX模型辨識結果的精度有待提高。

4 結論

在軌道不平順與車體橫向加速度相干分析基礎上確定狀態空間模型的輸入，分別在小于0.005 m-1和0.005～0.350 m-1兩個空間頻段上建立軌道不平順與車體橫向加速度之間的關聯模型，利用高速綜合檢測列車實測數據訓練優化關聯模型得到傳遞模型的合理階數及結構參數，模型的殘差近似符合零正態分布的假設。

對比實測軌道不平順及模型傳遞函數預測車體橫向加速度數據和實測車體橫向加速度結果驗證所構建的狀態空間模型傳遞函數的準確性，分析結果表明合理階數的狀態空間模型能夠較好地辨識軌道不平順與車體橫向加速度之間的傳遞關系。