核電廠數字化儀控系統軟件可靠性定量評估研究

黃 奇，張 慶，劉明星，王遠兵，鐘 科

(中國核動力研究設計院 核反應堆系統設計技術重點實驗室，四川 成都 610213)

隨著計算機技術的發展，改造與新建的核電廠逐步采用數字化儀控系統實現反應堆的保護和控制功能，數字化儀控系統的安全性和可靠性是核電廠平穩運行的關鍵。目前國內外對于數字化儀控系統硬件方面可靠性研究已取得了較大成就，然而對于數字化儀控系統軟件可靠性評估方面的研究基本還處于初始啟蒙狀態。

標準IEEE std 1633中將軟件可靠性評估模型分為3種通用類別，即呈指數分布的非齊次泊松過程模型(NHPP)、非指數分布的NHPP模型和貝葉斯模型。而Schneidewind模型是標準IEEE std 1633中推薦的一種呈指數分布的NHPP典型模型。由于該模型有一個基本思想，即部分測試周期中檢測的錯誤率受某些客觀因素影響，不能更好地對軟件未來的可靠性進行預計。

該模型有以下三種形式：模型1—利用n個時間單元中的所有錯誤計數。其基本出發點是所有數據點都同樣重要；模型2—忽略從第一個到第s-1個時期的錯誤數，即只使用從第s個時期到第n個時期之間的數據。其基本出發點是早期數據對預計未來行為作用很小；模型3—使用從周期1到s-1的累積錯誤計數，作為第一個數據點，而使用s到n的獨立錯誤計數作為其他數據點。此方法介于前兩個模型之間，反映了以下思想：前s-1個周期的數據組合可以預計以后階段的失效率。

本文結合IEEE std 1633標準中Schneidewind模型，以核電廠數字化儀控系統為研究對象，研究數字化儀控系統軟件可靠性的分析方法，并結合某堆型核電廠數字化儀控系統典型功能模塊的軟件故障數據進行研究。

1 Schneidewind模型構造

在利用該模型進行研究時，需進行以下假設：

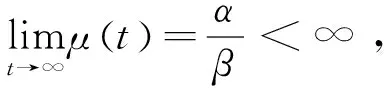
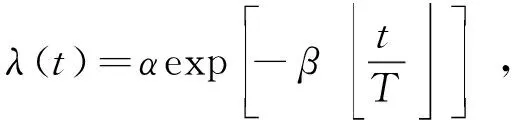
(3)每個時間間隔檢測出的錯誤數是相互獨立的；

(4)軟件運行方式與預期的運行使用方式相似；

(5)每個錯誤出現的機會相等，且各錯誤的嚴重程度相同；

(6)軟件的失效是相互獨立的；

(7)觀測軟件的時間間隔都相同。

根據假設，第i個時期的累積錯誤數均值為：

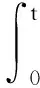
(1)

因此第i個時期的期望錯誤數為：

(2)

由于每個時間間隔檢測出的錯誤數fi為可獨立非均勻泊松隨機變量，可構建似然函數如下：

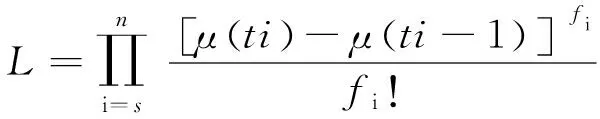
(3)

利用極大似然估計，可以得出三種模型的參數α，β的估計值。

(1)模型1

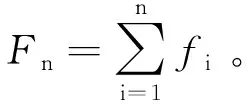
(2)模型2

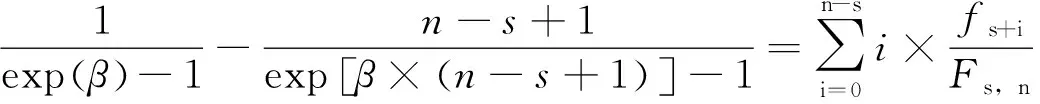
(3)模型3

2 數字化儀控系統軟件可靠性評估

根據某堆型核電廠數字化儀控系統典型功能模塊的軟件可靠性故障數據，以“周”為測試周期，對故障數據進行統計表1所示。

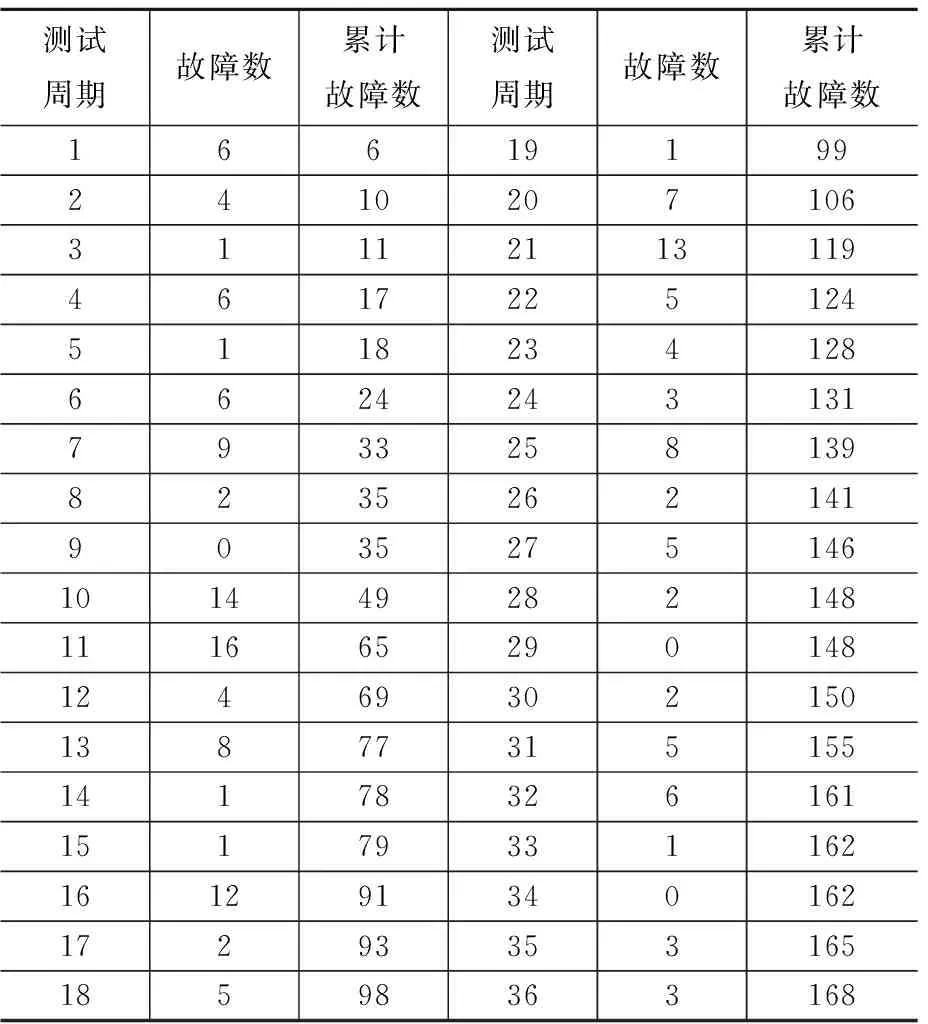
表1 故障數據統計(36周)Table 1 Fault data statistics(36 weeks)

從表1可以看出，該典型模塊功能軟件經過36個周期的測試，共發現168個故障。測試初期，故障發現率較高，隨著測試不斷深入，發現的故障不斷修復，通過測試發現的故障數量同比有所減少。從統計結果可以看出，數據滿足假設條件中任一周期期望的錯誤發生數與此周期的期望未檢測出的錯誤數成正比例的假設條件。

2.1 參數估計

根據軟件故障數據統計結果，將36周數據代入到第2章構建的模型1中，對參數α和β進行估計，得到估計值為：

α=6.386 419 403 300 72

β=0.018 446 464 462 79

參數α也稱為其初始失效強度。

2.2 軟件可靠性評估

累計失效數的計算公式如式(1)所示，通過對實際數據以及估計后擬合的曲線作圖如圖1所示。

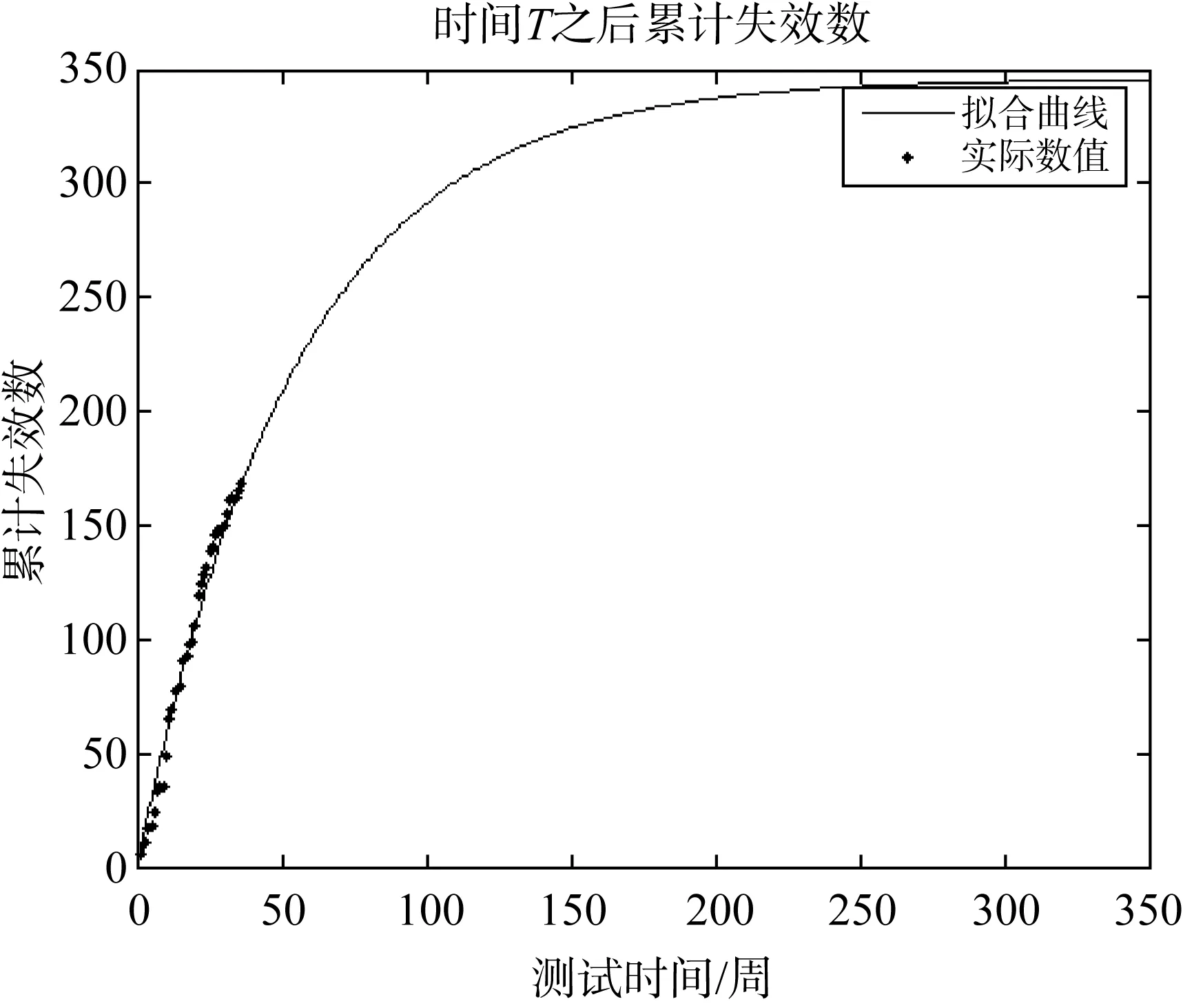
圖1 累計失效數隨測試時間的變化曲線Fig.1 Variation curve of cumulativefailure number with test time

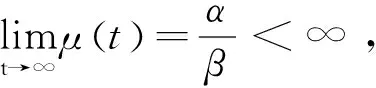
根據實際數據以及估計擬合的結果，可以得到數據方差MSE為：

MSE=65.75

殘余失效數的計算公式如式(4)所示：

(4)

通過該模型得到的軟件可靠度是一個分段過程，用R(tn+Δt)表示，其計算公式如式(5)所示：

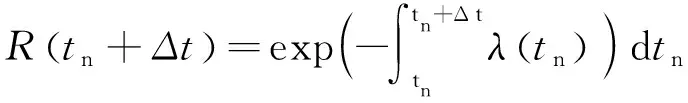
(5)

并且可以計算得出此時當測試周期為36時，軟件殘余失效數為178.2，如圖2所示。同時可以得到軟件可靠度隨著測試時間的變化曲線如圖3所示。

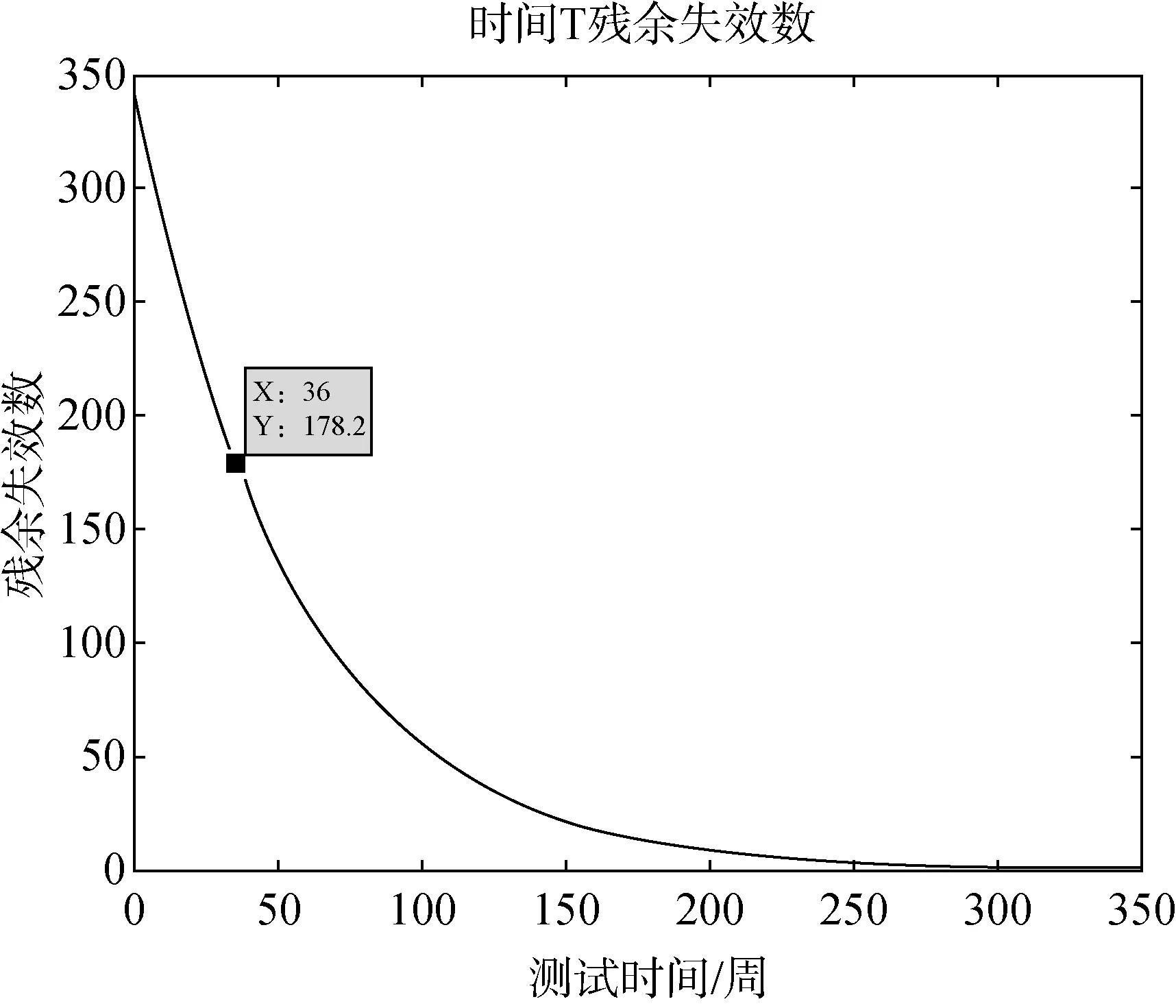
圖2 殘余失效數隨測試時間的變化曲線Fig.2 Variation curve of residualfailure number with test time

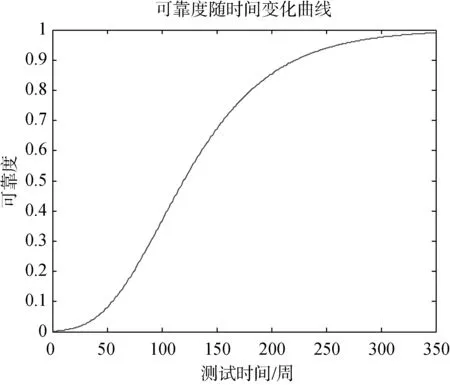
圖3 軟件可靠度隨著測試時間的變化曲線Fig.3 Variation curve of softwarereliability with test time

從預計結果顯示，軟件可靠度隨著測試時間趨近于指數變化形式，根據圖3所示結果，目前階段，還需要繼續對軟件進行測試以發現bug，從而提高軟件的可靠度水平，以滿足相關指標要求。

從該模型的預計計算結果顯示，該模型可用于指導相關人員進行軟件測試，明確何時應加大測試力量的投入、評估何時測試結束等。

3 模型評估與實際數據對比

根據上述驗證結果，測試周期36時，內部存在的故障還較多，還需繼續進行測試以發現bug并進行修復，進而提高軟件可靠性。通過繼續對軟件可靠性進行測試，得到測試結果如表2所示。

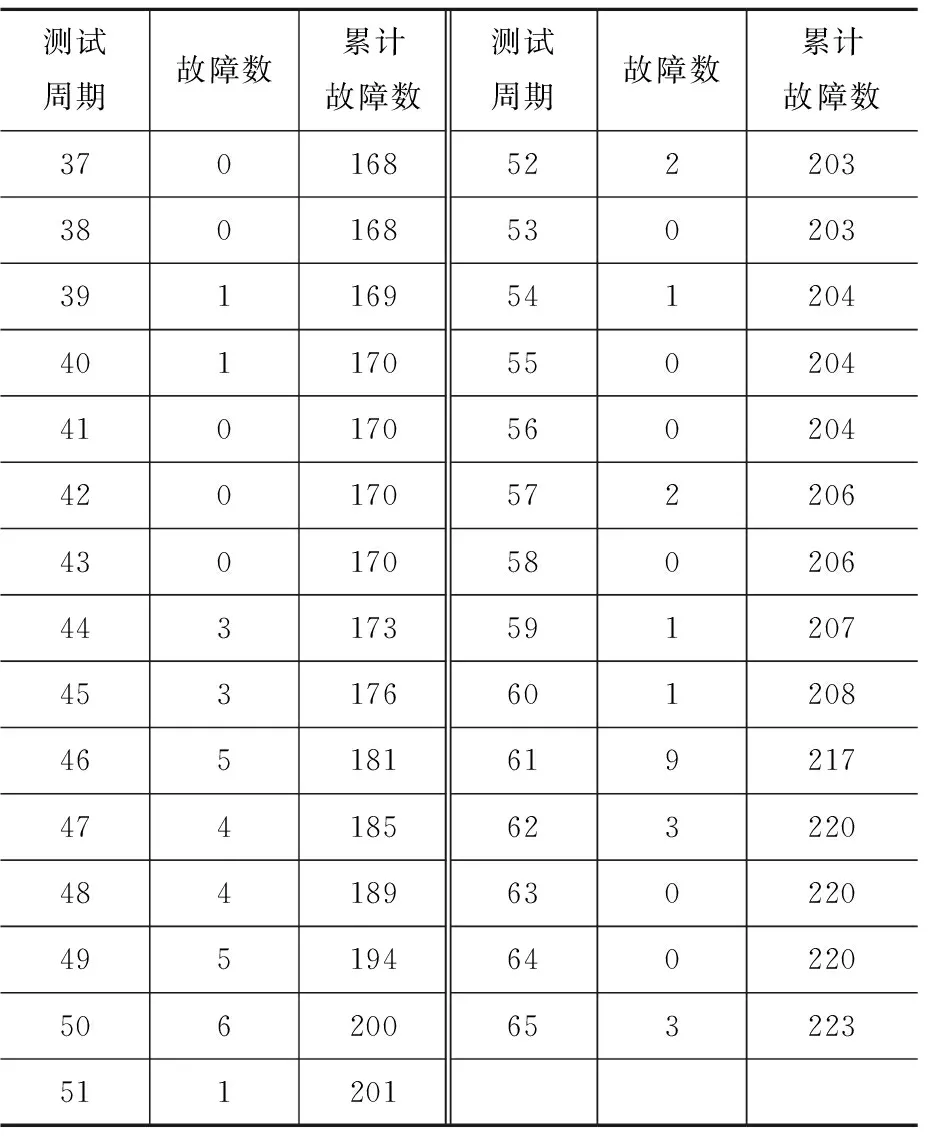
表2 故障數據統計(65周)Table 2 Fault data statistics(65 weeks)

將后續測試得到的結果與前期預期的結果進行對比，如圖4所示。

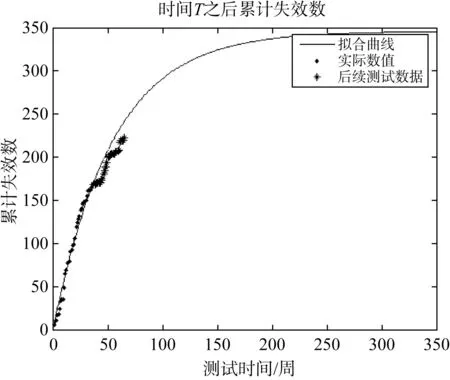
圖4 后續測試結果與前期預計結果對比Fig.4 Comparison of follow-up test resultswith previous expected results

根據圖4對比數據顯示，根據前36個測試周期得到的擬合結果基本與后續測試結果接近，但還是存在些許誤差，并且從圖中對比數據可以看出，隨著測試周期的逐步增加，誤差逐漸增大，因此在應用該模型對該堆型核電廠數字化儀控系統軟件可靠性進行預計評估時，需根據實際結果對模型估計參數進行不斷地迭代優化。

根據所有65周測試結果進行優化后得到的參數估計結果如下所示，優化后的曲線如圖5所示。

α=6.538 934 067 655 78

β=0.022 553 308 627 75

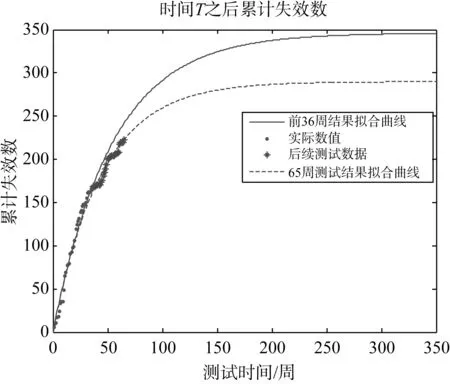
圖5 數據優化后的累積失效數曲線Fig.5 Cumulative failure number curveafter data optimization

4 總結

本文對IEEE std 1633中提到的Schneidewind軟件可靠性評估模型進行研究，并結合某堆型核電廠數字化儀控系統典型功能模塊軟件故障相關數據，研究Schneidewind模型對于核電廠數字化儀控系統的適用性。

本文對某堆型核電廠數字化儀控系統典型功能模塊的軟件可靠性進行評估，計算了軟件的累積故障數以及殘余故障數。通過評估結果發現，目前該堆型數字化儀控系統典型功能模塊的軟件還存在有殘余故障，將會影響該軟件可靠性，還需繼續對該堆型數字化儀控系統軟件進行測試，發現軟件bug并修復，從而提升軟件的可靠性，以使其滿足相關要求。

另外，應用該軟件可靠性定量評估模型對核電廠數字化儀控系統軟件可靠性進行定量評估時，能夠很好地對軟件可靠性進行擬合，但是隨著測試周期的逐步增加，需根據實際測試結果，不斷地對模型參數進行迭代優化，以貼近實際的結果，以利于有效地指導后續測試工作。同時，可以選擇不同的典型功能模塊，以實現其對整個儀控系統軟件可靠性評估的覆蓋性。