接觸式輪廓儀的自動標注數學模型

崔煜

摘要：為2020年全國大學生數學建模競賽D題提供可行解法，針對探針沾污、探針缺陷、掃描位置不準導致的輪廓儀數據不準問題，利用matlab對數據進行分段處理，進而確定水平線軸線，擬合曲線段，斜線段，確定交點坐標、利用基本的數學知識建立模型求解出工件直線段各個參數，用最小二乘法擬合和圓弧。針對有傾斜角的工件測量數據，利用旋轉變換法將有傾斜角度的工件測量數據水平校正。

關鍵詞：數據擬合;標注;最小二乘法;旋轉變換

1.問題的提出

輪廓儀是一種兩坐標測量儀器，它由工作平臺、夾具、被測工件、探針、傳感器和伺服驅動等部件組成。其工作原理是，探針接觸到被測工件表面并勻速滑行，傳感器感受到被測表面的幾何變化，在X和Z方向分別采樣，并轉換成電信號。該電信號經放大等處理，轉換成數字信號儲存在數據文件中。

輪廓曲線理想狀況下是光滑的，但由于接觸式輪廓儀存在探針沾污、探針缺陷、掃描位置不準等問題，呈現出粗糙不平的情況，這給工件形狀的準確標注帶來影響。

因此簡化問題，假設被測工件的輪廓線是由直線和圓弧構成的平面曲線（見圖4）。請建立數學模型，根據附件1（工件1的水平和傾斜測量數據）、附件2～附件4（工件2的多次測量數據）所提供的輪廓儀測量數據，研究下列問題：

問題1是根據附件1中的工件1在水平狀態下的測量數據即表level，其輪廓線如圖4所示，請標注出輪廓線的各項參數值：槽口寬度、圓弧半徑、圓心之間的距離、圓弧的長度、水平線段的長度、斜線線段的長度、斜線與水平線之間的夾角和人字形線的高度。

問題2是在同一工件在不同次測量時，由于工件放置的角度和位置不同，輪廓線參數的計算值也會存在差異。附件1中的表down給出了工件1在傾斜一個角度和有一些水平位移狀態下輪廓線的測量數據。請計算該工件測量時的傾斜角度，并作水平校正。在數據校正后，完成問題1的任務，并比較兩種測量狀態下工件1各項參數計算值之間的差異。

2.數據處理

通過初步分析，發現附件1中原始較為完整，不存在缺失和重復，數據精度比較高，到小數點后九位。而matlab中精度是小數點后四位，所以采用excel進行計算，采用matlab進行畫圖。

將工件1中level表格的數據導入matlab，利用畫圖函數可得如下圖1，為了更清楚明確的計算各個參數，分別在圖中標注了各個分段點，同時也將數據按點分段。

通過圖1可以看到水平線段有8段，圓弧有7段，人字高數據一段。

3.問題一模型的建立與求解

3.1模型的建立

由于工件1輪廓線中水平線在放大后粗糙凹凸不平，不能夠直接從圖形中選取分段點。假設工件水平面光滑，統計數據分析，擬合各個水平線段的直線方程。再與各個曲線擬合的方程聯立求解得出交點。

1、對于水平線，求8段數據的平均數

其中為第段水平數據段的平均值。

2、對于斜線建立直線模型

其中對于參數的設定用數據擬合方法。

3、由于水平線上拐角處凹凸不平，很難確定端點坐標，同時為了較為準確合理的求出工件的水平長度、夾角，利用曲線擬合數據來計算端點，對于每一條弧線假設滿足方程：

4、類似中學數學中求點的坐標的方法，分別聯立水平線和2條斜線方程

解方程可得的坐標。

5、類似中學數學中求點的坐標的方法，分別聯立水平線和曲線方程

解方程可得的橫坐標。

6、因此可以計算得出槽口寬度

7、為了方便求出夾角，三個鉛筆輪廓與水平線相交的上部分近似的看成直線段，擬合出直線段的直線方程

8、鉛筆輪廓上半段直線、斜線與水平線之間的夾角的正切為，則斜線與水平線之間的夾角為

9、斜線的方程（2）已給出，假設斜線段是直線斜線，其長度為

10、對于工件中圓弧部分要求出圓心和半徑，建立圓的方程

下面我們采用最小二乘法來進行擬合[5]，因此設最小二乘圓的一般方程為

擬合誤差的平方和為由最小二乘法原理求得的參數使得最小，必須讓、和通過對系數求偏導并令其導數為零，可得

通過求解上述矩陣方程可得一般圓的方程系數，通過圓的方程變換可得擬合圓的半徑和圓心坐標如下：

11、圓心之間的距離

12、對于圓弧長的求解，我們利用圓弧長公式

其中是圓的半徑，為圓弧對應的圓心角，當圓弧與水平面相交時（大小圓弧），交點為。

對于的求解利用余弦定理得出

當圓弧不與水平面相交時（鉛筆輪廓），聯立圓的方程與直線方程得

（17）

解方程組可得圓弧左邊交點，圓弧右邊交點

由弧與左右直線相交交點與圓心構成等腰三角形，兩腰夾的角利用余弦定理可求得，公式如下：

3.2模型的求解

3.2.1槽口寬度求解

如圖1所示，槽口寬度即兩個橫坐標之間的差值，只要把橫坐標求出來即可。要通過求交點求出橫坐標，則先把曲線的方程擬合出來，通過matlab工具箱cftool把工件1中10段曲線數據段和兩段直線數據段擬合出來，其中前三個凸出來的鉛筆頭輪廓，分成兩端進行擬合，是為了提高擬合精度，結果如下表：

通過（4），（5）和（6）三個方程組通過解得的橫坐標如下表

其中和為數據的起始點。

利用水平端點的坐標數據，橫坐標做差得到槽口寬度如表3

3.2.2人字形高度及斜線長度求解

兩條斜線之間的交點可以通過聯立兩直線方程

可得兩直線的交點Z坐標（），人字形高可以通過減去水平線高。

由excel軟件求解得人字形高位0.9868。

對于斜線段得長度得求解，下端點分別為上端點坐標為（）因此斜線段長度為：

3.2.3斜線與水平線之間的夾角求解

為了簡化計算，將三個鉛筆輪廓與水平線相交的上部分近似的看成直線段，數據上選取部分數據作直線擬合，而對于斜線段直接選取數據擬合，求出得8條直線方程、斜率和斜傾斜角如下表：

3.2.4圓心、圓的半徑及弧長的求解

首先由最小二乘法擬合出圓的方程如下表

因此可以求出圓心距如下表

利用matlab求解曲率為零的點，然后利用定積分求解每一段弧如下表

4.問題二模型的建立與求解

4.1模型的建立

附件1中的表down給出了工件1在傾斜一個角度和有一些水平位移狀態下輪廓線的測量數據，計算該工件測量時的傾斜角度，并作水平校正。

對于工件1傾斜角角度的求解，從圖形中選取斜線段設

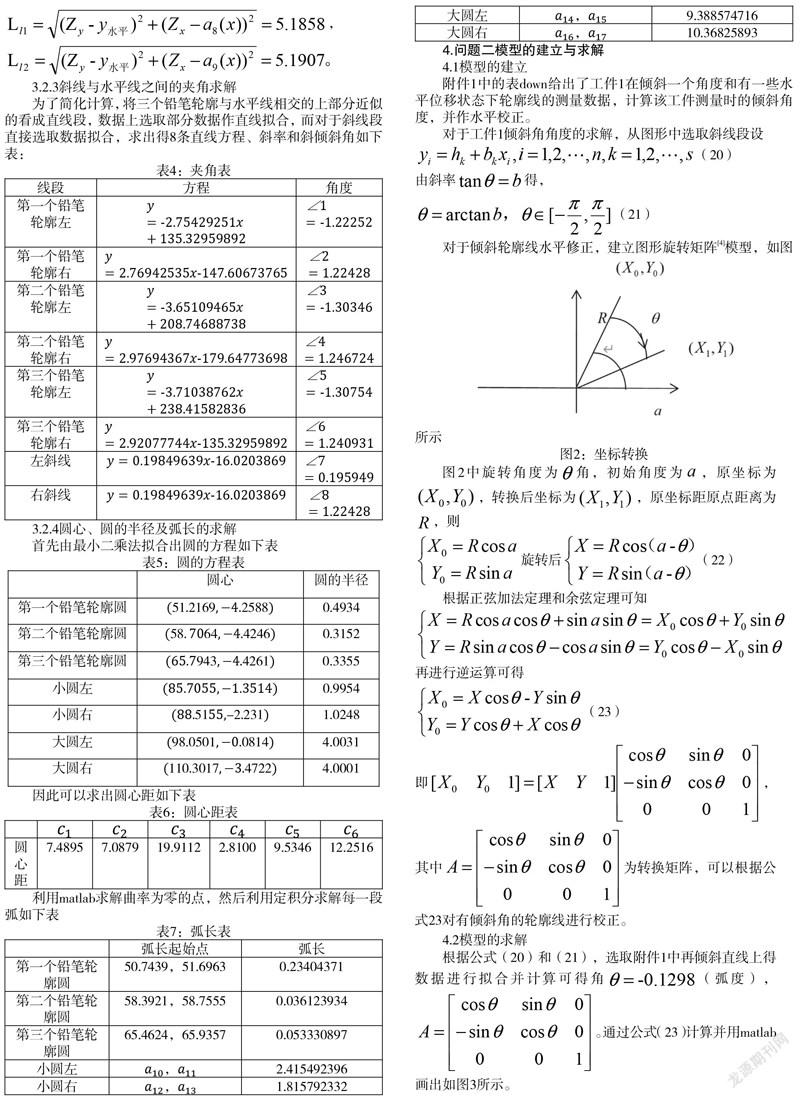
對于傾斜輪廓線水平修正，建立圖形旋轉矩陣[4]模型，如圖所示

圖2中旋轉角度為角，初始角度為，原坐標為，轉換后坐標為，原坐標距原點距離為，則

根據正弦加法定理和余弦定理可知

再進行逆運算可得

即，其中為轉換矩陣，可以根據公式23對有傾斜角的輪廓線進行校正。

4.2模型的求解

根據公式（20）和（21），選取附件1中再傾斜直線上得數據進行擬合并計算可得角（弧度），。通過公式（23）計算并用matlab畫出如圖3所示。

在數據校正后，采用與問題一同樣的計算方法，對上圖中的輪廓線相關參數進行求解。求得的結果與圖一中相關數據進行對比。

4.2.1槽口寬度

先對斜線，圓弧進行數據擬合，然后通過直線的方程和圓的方程計算出端點的橫坐標。

利用水平端點的坐標數據，橫坐標做差得到槽口寬度如表3

4.2.2人字形高度及斜線長度求解

由excel軟件求解得。對于斜線段的長度得求解，下斷點分別為，上端點坐標為（）因此斜線段長度為：，。

4.2.3斜線與水平線之間的夾角求解

為了簡化計算，將三個鉛筆輪廓與水平線相交的上部分近似的看成直線段，數據上選取部分數據作直線擬合，而對于斜線段直接選取數據擬合，求出得8條直線方程、斜率和斜傾斜角如下表：

4.2.4圓心、圓的半徑及弧長的求解

首先由最小二乘法擬合出圓的方程如下表

因此可以求出圓心距如下表

利用matlab求解曲率為零的點，然后利用定積分求解每一段弧如下表

5.結論

本文對探針沾污、探針缺陷、掃描位置不準等問題帶來的數據不準問題，建立數學模型對工件形狀相關參數準確標注，建立模型所運用的數學知識簡單易懂，計算方法簡單易行。對于圓弧圓的半徑和圓心的求解，利用最小二乘法擬合，較為理想的確定圓的半徑和圓心，提高數據的準確性，實現輪廓線自動標定。對于有傾斜一個角度的工件數據，采用旋轉變換實現數據調整為正常狀態。

參考文獻：

[1]趙琦，解琳琳，侯妙樂，劉浩宇.基于點云數據的雀替輪廓線參數信息自動化提取方法[J].地理信息世界，2018年，第25卷第5期

[2]韓志國，李鎖印，馮亞南，趙琳.接觸式輪廓儀探針狀態檢查圖形樣塊的研制[J]，微電子技術，2019年第9期

[3]陳十進，劉瑾，楊海馬，劉海珊，韋鈺，肖俊，解光耀.非接觸式鋼軌三維輪廓參數檢測系統研究[J].儀表技術與傳感器，2019年第5期

[4]閆志剛，圖形學中繞任意軸旋轉矩陣的推廣[J].計算機時代，2009年第12期

[5]楊旭東，大量程輪廓綜合測量系統研究[J].華中科技大學博士論文.2007年5月

[6]司守奎，孫兆，數學建模算法與應用[M].國防工業出版社.2015年4月（第二版）

[7]姜啟源，數學模型[M]，高等教育出版社，2008年3月（第三版）

（浙江交通職業技術學院 人文學院?杭州?311112）