DEM-FDM耦合分析海底管線拋石保護層抗錨害能力

程志遠， 李 黎， 肖 鵬， 亓麗芳

（1． 湖北第二師范學院建筑與材料工程學院，武漢430205；2． 華中科技大學控制結構湖北省重點實驗室，武漢430074）

0 引 言

海洋油氣開發中，為了防止海底管線（油氣管道、臍帶纜、海底電纜、光纜等）遭到拋錨等墜落物的砸傷損壞，通常應根據不同的海床、地質情況采取不同的保護措施，如沖埋保護、套管保護、混凝土壓塊、砂袋回填、水下拋石等［1］。針對海底管線在復雜海床地質條件下形成的懸空段，綜合考慮經濟、技術等因素，通常實施拋石填充保護方案，即用專門的拋石船在管線上方拋集由不同級配石子形成的石料堆積體，具有一定抵御船錨沖擊破壞的能力。拋石技術應用于海底設施防護工程起始于20 世紀70 年代，Frans船首次將砂石拋于采油平臺的樁腿周邊，之后Rocky Giant船將石料用于海底管線的保護。我國在1999 年首次引進拋石技術，當時對平湖油氣田海底管道岱山海域及上海蘆潮海域海底管道懸空段共回填碎石14 km3［2］。近年來，隨著拋石船和落管拋石水下機器人（ROV）的快速發展［3］，水下拋石作為一種海底管線的保護措施之一，在國內外海洋工程中已得到廣泛應用，現已由淺水應用到深水。

目前國內外對海底管線拋石防護工程的研究主要集中于管線選型、線路規劃、拋石的采集和施工等方面［4-8］，而對于拋石防護后海底管線的安全性還缺乏定量研究。海底管線抵御船錨侵害涉及離散和連續兩種不同尺度介質的相互作用。其中船錨和管線屬于連續介質，拋石保護層屬于離散介質。對于此類問題，目前國內外用于分析的數值手段主要包括有限元法（Finite Element Method，FEM）、有限差分法（Finite Difference Method，FDM）等連續介質方法和用于離散介質的離散單元法（Discrete Element Method，DEM）。連續體法在解決連續體問題時計算效率高，但是用來模擬堆石體時無法反映內部顆粒流動和力鏈的分布情況。文獻［9］中由于用連續體法模擬離散區域而導致模擬值比實測值高34%。如果僅采用離散介質方法，即將連續介質海纜和船錨也用離散顆粒近似表示，并統一用DEM求解［10-11］。雖然該近似法有一定的理論基礎，但是船錨和管線畢竟為連續介質，將其等效為剛性的顆粒是否合理，其精度是否滿足要求等問題還有待進一步探討，而且還會增加模型的顆粒單元數目，計算時間過長。鑒于單獨使用連續體法或離散元法模擬的不足，本文采用FDM發揮連續體法計算速度快的優點用來模擬船錨和海纜，并采用DEM模擬堆石體以真實反映船錨侵入其中顆粒流動的情況，建立DEMFDM耦合作用模型，研究海底管線拋石保護層的抗錨害能力特性。

1 DEM-FDM耦合模型

Itasca公司推出的2 款應用軟件PFC3D和FLAC3D的Socket I／ O 功能可以支持DEM-FDM 的耦合計算［12-13］，本研究采用DEM-FDM 耦合的建模方法模擬海底管線拋石保護層的抗錨害能力，其耦合建模的具體特點是：在模型的建立過程中，使用FLAC3D將船錨和海底管線離散成連續的單元體，建立有限差分網格，使用PFC3D將海底管線拋石保護層離散成非連續的顆粒集合。在每一次計算中，FLAC3D先從PFC3D中接收顆粒傳來的力和力矩，作為對應連續體的單元荷載，再據此計算出連續體單元的變形；計算完成后，又將連續體表面的單元的速度傳遞給PFC3D作為顆粒集合相應墻體的端點速度，由此實現船錨與拋石保護層、拋石保護層與海底管線之間界面的變形協調。根據圖1 所示流程，即可實現離散、連續兩區域的耦合計算。

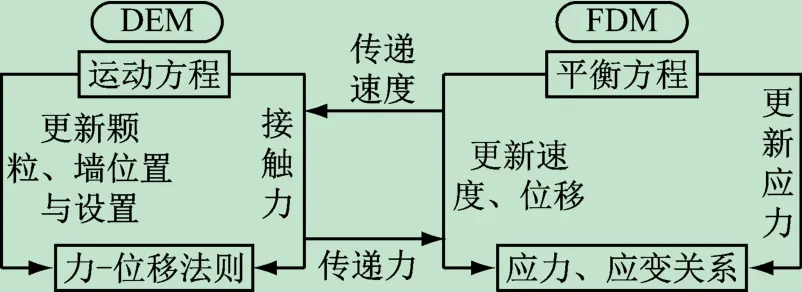
圖1 有限差分、離散元耦合計算流程圖

為了驗證數值算法的正確性并評估誤差，本文設計了落錨的室內縮尺實驗，即將船錨起吊到不同高度并使之自由下落侵入拋石保護層，落錨位置在堆石體中間。實驗過程中主要測量船錨侵入拋石保護層深度以及海纜表面的側壁壓力，并與理論值對比。為了研究不同落錨初始速度下拋石保護層的抗錨害能力，本文進行了不同高度下的落錨實驗，實驗工況的豎直高度分別取0 ～3 m，間隔0． 5 m，為了降低實驗過程中偶然誤差的影響，同一落錨高度進行3 次獨立重復實驗，實驗結果取3 次實驗的平均值。落錨時先用細鋼絲繩將船錨與吊車鐵鉤相連，然后將船錨起吊到相應高度，待船錨靜止時，將鋼絲繩剪斷，這時船錨將自由落下侵入拋石保護層，待落錨完畢（測點壓力值不再變化）時，測量船錨的最終侵入深度，并在PC 終端上保存測點處的應力值，最后將船錨移開，重新堆積碎石到初始形狀，準備下組實驗。落錨實驗如圖2 所示。

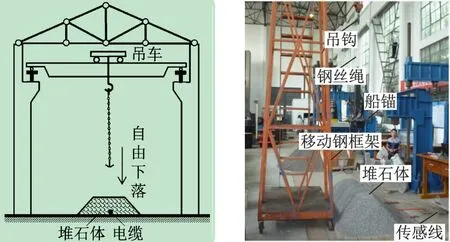
圖2 落錨實驗方案

其中，離散介質堆石體材料為粒徑10 ～20 mm的碎石，顆粒形態以四面體為主，重度約為27 kN／ m3，近似服從均勻分布。數值計算方法中，堆石體顆粒的顆粒剛度和摩擦系數并未給出，因此這里需要補充側限壓縮實驗和直剪實驗測量這兩個參數［14］，通過實驗可以測得實驗用拋石顆粒的摩擦系數為0． 46，剛度為2． 87 GN／ m。影響拋石保護層顆粒生成的因素很多，主要包括：顆粒級配曲線、顆粒邊數、位置坐標等。依據每組顆粒尺寸的上界和下界，可以在此上下界區間均勻隨機取值直到顆粒含量滿足要求為止。本實驗的堆石體設計成梯形截面：上底寬0． 5 m，下底寬1 m，高0． 5 m，堆石體縱向長2 m。根據以上方法就可以確定拋石保護層顆粒的含量、粒徑和邊數，再將顆粒在指定的區域內均勻隨機投放直到符合要求為止，這樣就得到了拋石保護層顆粒在PFC3D中的堆積模擬試樣，如圖3 所示。

圖3 拋石保護層堆積模型

海底管線屬于比較規則的連續體，可以直接在FLAC3D中建立有限差分模型，如圖4 所示。

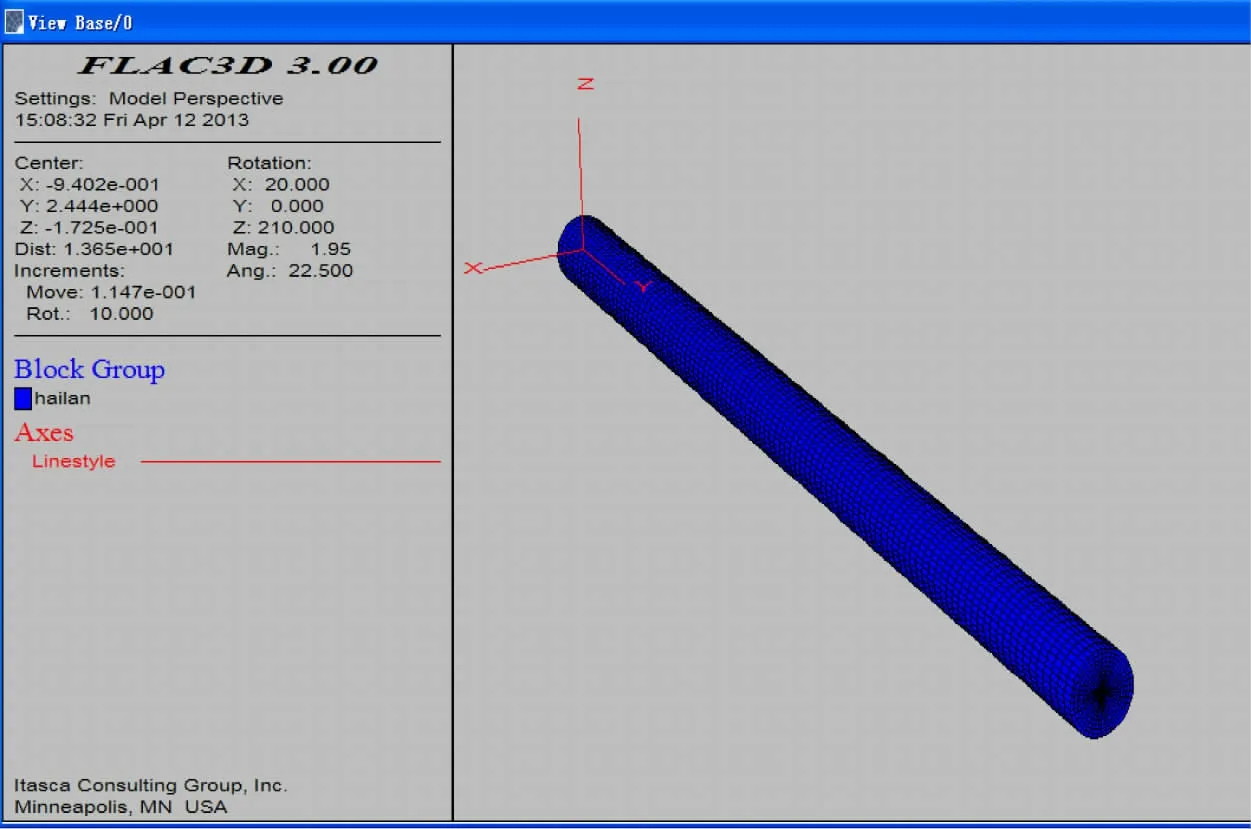
圖4 海底管線的有限差分網格

船錨選用200 kg霍爾錨，船錨屬于比較復雜的實體模型，包含大量的曲線段，在FLAC3D中建模存在困難。因此，數值模擬首先借助建模功能強大的ANSYS軟件建立模型，彌補FLAC3D建模功能的不足，并開發編寫“ANSYS-FLAC3D”接口程序，將ANSYS 建立的模型導入到FLAC3D中形成有限差分網格，如圖5 所示。

圖5 船錨的有限差分模型

這里因為使用FLAC3D建立船錨和海底管線的連續體模型，還需要知道這兩者的物理力學參數，如表1所示。

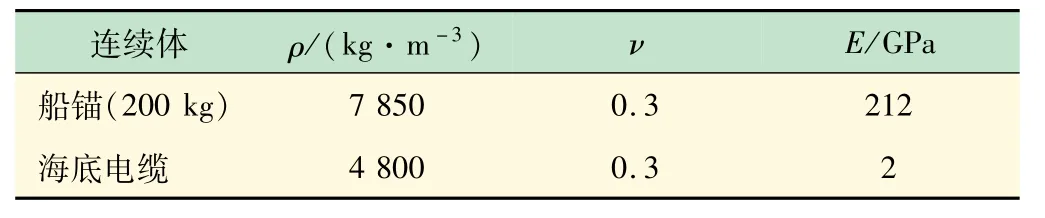
表1 連續體的物理力學參數

拋石保護層、海底電纜、船錨模型建立以后，即可按DEM-FDM 法進行耦合計算，得到拋石保護層的抗錨害能力。

2 仿真與實驗結果對比分析

2.1 船錨侵入深度

為了保證海纜不會被船錨勾壞，工程上要求船錨的侵入深度小于海纜的埋置深度。圖6 顯示船錨侵入深度的計算值明顯小于實驗值，數值仿真中堆石體顆粒粒徑是嚴格服從均勻分布的，但是實際的顆粒樣本不可能完全服從這種分布，這樣就造成實際的堆石體的孔隙率比仿真模型值大，參與耗能的顆粒少，因此船錨侵入深度的實驗值比理論計算值大，這也是本文實驗部分的一項不足；另外，PFC3D中的顆粒參數與相應實際值的差別也可能是導致計算值小于實驗值的原因。

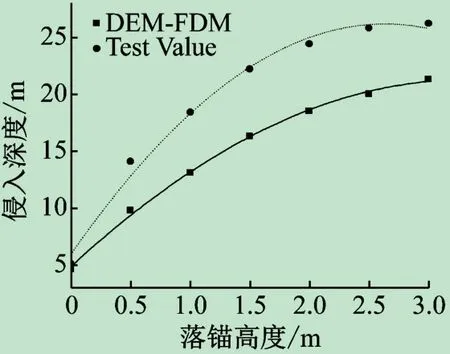
圖6 船錨侵入深度的實驗值與計算值對比

2.2 海纜側壁壓力

船錨沖擊侵入拋石保護層的過程中，堆石體通過內部“力鏈”的重組將沖擊力分散并向下傳遞，并在海纜表面形成一定的側壁壓力，Albert 等［16］通過實驗表明該壓力在侵入過程中不斷波動。工程實踐中關注該壓力的峰值，如果該壓力峰值大于海纜的側壁承壓，海纜會遭受破壞；反之，則不會。實驗中，3 個壓力傳感器安置在海纜表面的4 等分點處，用于測量該處的壓力峰值。

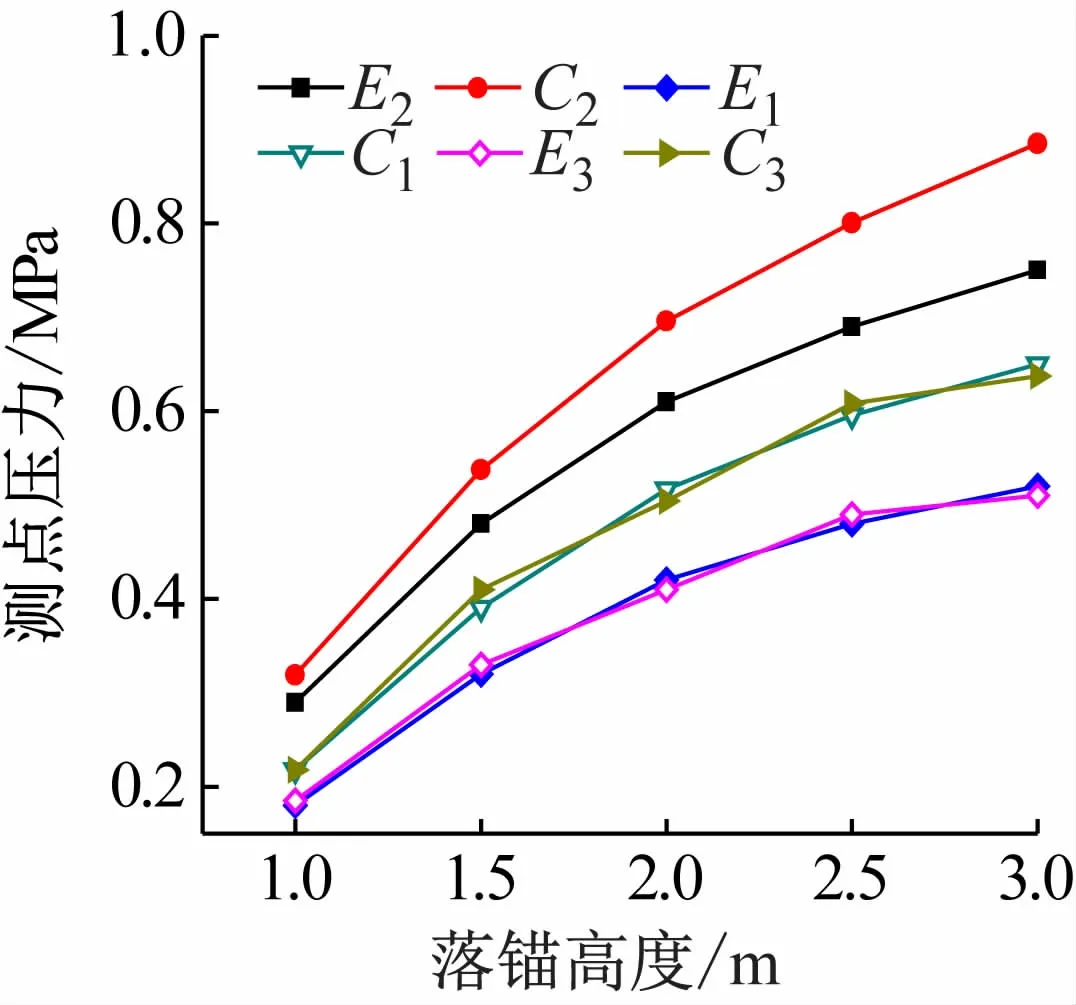
圖7 不同落錨高度時測點的土壓力峰值

圖7 中，E代表實驗值，C代表計算值，下標1、2、3代表對應的測點。由圖可以看出，對于海纜表面的壓力峰值，計算值較實驗值偏大，這正好與侵入深度的規律相反。由于船錨侵入的深度越深，船錨與堆石體作用的時間越久，顆粒間摩擦碰撞的時間越長，耗散的能量更多，堆石體對船錨沖擊的緩沖作用越強，這樣在海底管線表面產生的土壓力也就越小。由圖還可以看出，理論計算值與實驗值的誤差隨落錨高度，即落錨初始速度的增加而增加，在3 m 高度自由落錨時（初始速度7． 75 m／ s），計算值與實驗值相差12%左右，說明該數值方法合理、可行，具有一定的精確度。

3 工程實例

3.1 工程概況

500 kV南方主網與海南電網聯網工程中，海纜鋪設工程北起廣東省徐聞縣，穿越瓊州海峽到達海南省玉苞角。海纜路線上每天有各種商船經過，雖然在航線上明令禁止拋錨，但這種情況還是經常發生。為了保證海底電纜安全運營，有必要對其抗錨害安全性能進行研究。

《電力工程電纜設計規范》（GB50217—2007）規定：水下電纜不得懸空于水中，淺水區埋深不宜小于0． 5 m，深水航道區不宜小于2 m。同時，在綜合考慮海底電纜安全性和堆石體穩定性的情況下，拋石保護層經初步設計采用兩層結構［15］，內層（濾層）為25． 4～50． 8 mm 粒徑的碎石，外層（鎧裝層）為50． 8 ～203． 2 mm粒徑的塊石。通過設計論證，堆石體的石料最終選擇海山玄武巖巖層，原石發育穩定，儲量豐富并且易于開采和運輸。開采的原石經破碎后，按設計級配比例摻合。通過實驗，得出顆粒參數如下：重度26． 5 kN／ m3，剛度3 GN／ m，摩擦系數0． 35，泊松比0． 18，彈性模量70 GPa。石料經檢驗合格后即進入拋石作業。

由于此段海域經過的船只種類較多，船上裝載的船錨也多種多樣，為了保證一般性的前提下簡化工況，這里僅采用2 100 kg和1 440 kg兩種典型的霍爾無桿錨。本工程采用挪威Nexans公司生產的500 kV自容式單芯充油電纜，鉛合金護套、單層銅鎧裝，直徑約139 mm，最大允許的側壁承壓17 kN／ m。

3.2 計算結果及分析

船錨和拋石在水中均采用浮重度表示，通過耦合計算，可以得到兩種船錨以2． 5 m／ s的速度沖擊拋石保護層時的計算結果，其中船錨所受拋石阻力與侵入位移的關系如圖8 所示。

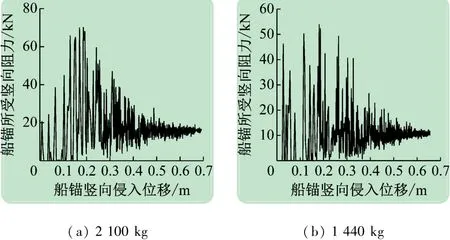
圖8 船錨所受阻力與豎向侵入位移的關系

由圖8 可以看出，隨著船錨侵入位移的增加，拋石保護層對船錨的阻力呈不斷波動的狀態，這是由于船錨侵入過程中，顆粒不斷運動，顆粒的位置以及應力分布不斷變化，導致堆石體內部力鏈不斷的變化和重組，該結果與Albert 等［16］、杜學能等［17］所做顆粒流實驗的變化趨勢是一致的。同時還可以發現拋石保護層對船錨的阻力是在某一常數附近波動，并最終收斂于這一常數，該常數是船錨的重力，這與實際情況也是相符的。隨著船錨豎向侵入位移的增加，拋石保護層會把力分散傳遞到海底電纜，并在海底電纜的側壁上產生側壁壓力，通過計算可以發現側壁承壓的最大值點在落錨點的正下方，即堆石體的幾何中心處，該處的側壁承壓值與船錨侵入位移的關系如圖9 所示。

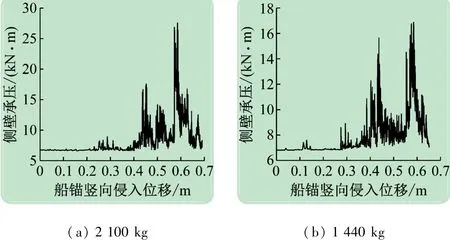
圖9 側壁承壓與豎向侵入位移的關系

由圖9 可以看出，隨著船錨侵入位移的增加，由拋石保護層傳給海底電纜的側壁壓力值也呈不斷波動的狀態。在落錨初期，側壁壓力值較小，隨著侵入位移的進一步增加，海底電纜的側壁壓力值才會有較大波動，并最終穩定。這是因為在落錨初期，由于拋石顆粒之間存在較大空隙，船錨的附加力會逐漸壓實這些空隙，顆粒之間開始有應力和相對運動的趨勢存在，堆石體內部力鏈開始逐漸形成，但是此時船錨附加力還來不及傳遞給海底電纜，導致此時其表面壓力較小。但是隨著船錨侵入位移的增加，空隙逐漸壓實，顆粒之間的應力變化和相對運動加強，力鏈開始變化和重組，船錨所產生的附加壓力值就會逐漸傳給海底電纜，使得海底電纜所承受的壓力值逐漸增大，并最終穩定，這種變化過程真實反映了在拋石保護層內部力鏈從產生到波動并最終到穩定的過程。通過計算發現，對于2 100 kg船錨，其產生的最大側壁承壓峰值達到了27． 5 kN／ m，超過了該種海纜的側壁承壓限值（17 kN／ m），海纜會發生破壞，而對于1 440 kg船錨，最大側壁承壓值為16． 8 kN／ m，沒有超過該種海纜的側壁承壓限值，拋石保護層對海底電纜起了很好的保護作用。

4 結 論

本研究采用DEM-FDM 耦合計算方法，定量得到了拋石保護層的抗錨害能力，該方法具有一定精度，能為后續拋石保護工程設計提供理論依據。其主要結論如下：

（1）DEM-FDM耦合算法能夠較真實地模擬離散介質和連續介質的相互作用，計算結果基本符合實際情況。

（2）堆石體顆粒粒徑分布越不均勻，孔隙率越大，船錨侵入堆石體的過程中參與摩擦耗能的顆粒越少，實際侵入位移越大；同時由于孔隙率越大，船錨與堆石體的作用時間越長，力鏈分布的范圍更廣，其在海纜表面形成的壓力也越小。

（3）拋石保護層對海纜抵抗船錨沖擊有較好的保護作用，其通過顆粒間的摩擦耗能，將沖擊荷載分散并傳遞到海底管線，并在海底管線表面形成一定的土壓力，并且該壓力不是常數，而是隨著作用過程呈波動狀態，反映了堆石體內部力鏈從形成、重組到趨于穩定的過程。