例談中考題中的變化率問題
文 曹 丹
建立一元二次方程模型可以解決日常生活和社會實踐中的許多問題,求變化率問題是一元二次方程的主要應用。下面,我們結合中考真題,談談變化率問題的解題策略。
例1(2019·黑龍江哈爾濱)某商品經過連續兩次降價,售價由原來的每件25元降到每件16元,則平均每次降價的百分率為( )。
A.20% B.40% C.18% D.36%
【解析】本題是典型的平均降低率問題,可通過列表的方法來構建出問題變化的本質。設平均每次降價的百分率為x。
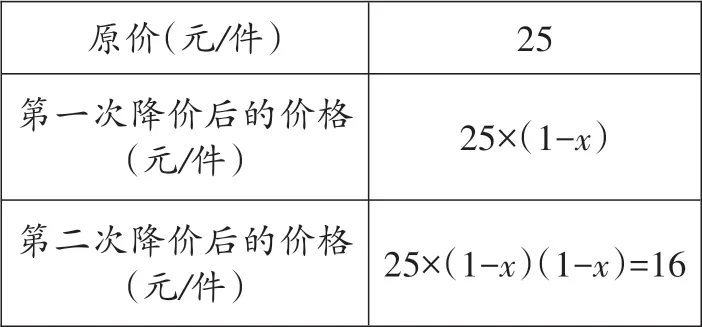
則25(1-x)2=16,解這個方程,得x1=20%,x2=180%(不符合題意,舍去),選A。
【點評】增長(降低)率問題的一般規律是:假設起始數為a,每次增長(降低)率為x,n為增長(降低)的次數,則一次變化后的數據是a×(1±x),2次變化后的數據是a×(1±x)2,n次變化后的數據是a×(1±x)n。設終端數為b,則我們得到一個模型:a×(1±x)n=b,那么對于平均增長(降低)率問題,應用模型可直接列方程解決。
例2(2019·湖南長沙)近日,長沙市教育局出臺《長沙市中小學教師志愿輔導工作實施意見》,鼓勵教師參與志愿輔導。某區率先示范,推出名師公益大課堂,為學生提供線上線下免費輔導。據統計,第一批公益課受益學生2萬人次,第三批公益課受益學生2.42萬人次。
(1)如果第二批、第三批公益課受益學生人次的增長率相同,求這個增長率。
(2)按照這個增長率,預計第四批公益課受益學生將達到多少萬人次?
【解析】(1)設這個增長率為x,則2×(1+x)2=2.42,
解這個方程,得x1=10%,x2=-210%(不符合題意,舍去)。
答:增長率是10%。
(2)2.42×(1+10%)=2.662(萬人次)。
答:預計第四批公益課受益學生將達到2.662萬人次。
【點評】問題(1)是一個標準的平均增長率問題,解決此類問題的關鍵是要弄清楚增長(降低)的含義是什么,問題的起始數是什么,經過幾次變化后的終端數是什么。這幾個問題弄清楚了,利用平均增長率模型:a×(1±x)n=b,就可以很快解決問題。問題(2)要求出第四批人數,第一問已經將平均增長率求出來了,此題就是個純計算問題了。
例3(2019·四川達州)某公司今年4月的營業額為2500萬元,按計劃第二季度的總營業額要達到9100萬元。設該公司5月、6月這兩個月的營業額的月平均增長率為x。根據題意列方程,則下列方程正確的是( )。
A.2500(1+x)2=9100
B.2500(1+x%)2=9100
C.2500(1+x)+2500(1+x)2=9100
D.2500+2500(1+x)+2500(1+x)2=9100
【解析】由題設可得5月營業額為2500(1+x)萬元,6月營業額為2500(1+x)2萬元,具體如下表:
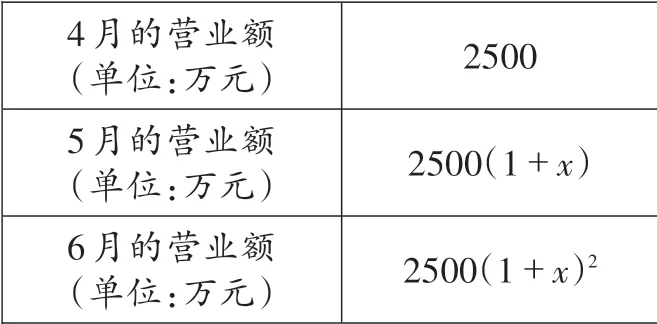
第二季度包括4月、5月和6月,故第二季度的總營業額為[2500+2500(1+x)+2500(1+x)2]萬元,所以可列方程為2500+2500(1+x)+2500(1+x)2=9100。選D。
【點評】本題不能錯誤地將方程列為2500(1+x)2=9100。這里的9100是第二季度的總營業額,也就是4、5、6三個月的總營業額,并非“終端數”。“終端數”是指某一個數量經過一次或多次變化后的數量,而不是變化后幾個數量的和,這個我們一定要分清楚。
例4(2020·重慶)“中國人的飯碗必須牢牢掌握在咱們自己手中”,為優選品種,提高產量,某農業科技小組對A、B兩個小麥品種進行種植對比實驗研究。去年A、B兩個品種各種植了10畝。收獲后A、B兩個品種的售價均為2.4元/kg,且B的平均畝產量比A的平均畝產量高100kg。A、B兩個品種全部售出后,總收入為21600元。
(1)請求A、B兩個品種去年平均畝產量分別是多少。
(2)今年,科技小組加大了小麥種植的科研力度,在A、B種植畝數不變的情況下,預計A、B兩個品種平均畝產量將在去年的基礎上分別增加a%和2a%。由于B品種深受市場的歡迎,預計每千克價格將在去年的基礎上上漲a%,而A品種的售價不變。A、B兩個品種全部售出后,總收入將在去年的基礎上增加%,求a的值。
【解析】(1)設A品種去年平均畝產量為xkg,則B品種去年平均畝產量為(100+x)kg。
由 題 意,得10×(x+100+x)×2.4=21600。
解這個方程,得x=400,則100+x=500。
答:A品種去年平均畝產量為400kg,B品種去年平均畝產量為500kg。
(2)此題涉及A、B兩個品種平均畝產量與B品種的單價、總收入這四個數量的變化,這是與上述幾個例題的不同之處(上述幾例只涉及一個數量的兩次變化)。此題A、B兩個品種平均畝產量這兩個數量只經過一次變化,B品種單價與總收入這兩個數量也只經過一次變化,我們可以將這四個數量的變化關系通過表格的形式表示出來。
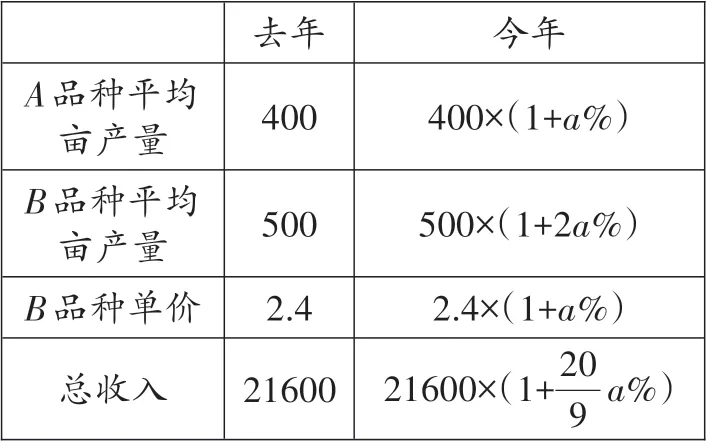
根據總收入=A品種收入+B品種收入,即總收入=A品種單價×A品種平均畝產量×A品種畝數+B品種單價×B品種平均畝產量×B品種畝數,可列出方程:
解這個方程,得t1=0(不符合題意,舍去),t2=0.1。
故a=10。
【點評】此題以民生為背景考查增長率,具有實際意義。此題中四個數量各經過一次變化,而這幾個數量內部之間存在一定的制約關系(總收入=A品種收入+B品種收入),那么我們就可以根據這種制約關系來列方程求解。題目中把平均增長率問題和幾個數量中每一個數量經過各一次增長的問題進行綜合,更考驗大家對數據的處理能力。
解這類問題,還要注意兩點:一是設增長率(降低率)為x,而不設為x%,這樣能簡化計算,所以例4解答過程中令a%=t;二是要根據題目的實際意義檢驗結果的合理性。

