模糊數學隸屬函數建模在電動汽車充電負荷預測中的應用

張笑迪 趙璧 任彬 宋堅瑞 劉吉昀 王亨達

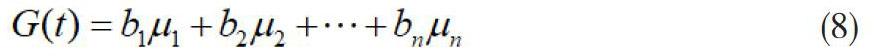
摘? ?要：隨著電動汽車規模化發展，其充電負荷將對電網產生一定影響。為了對電動汽車的充電負荷進行預測，文中討論了日行駛里程和用戶停車、充電行為習慣等充電負荷影響因素。針對區域內電動汽車充電可能性時間，采用模糊數學隸屬函數構建的方法，構造了電動汽車充電可能性曲線，確定了基于需求側的用戶充電時間的電動汽車日充電負荷曲線。通過與常規方法的比較，可以確定采用本文方法得到的預測結果具有較高的準確度，該預測方法可以應用于電動汽車充電負荷預測。

關鍵詞：電動汽車? 充電負荷? 區間數? 隸屬函數? 充電可能性曲線

中圖分類號：TM73? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼：A? ? ? ? ? ? ? ? ? ? ? ? 文章編號：1674-098X（2020）06（c）-0097-02

電動汽車充電受許多因素影響，表現出復雜的隨機性。微觀上，單一車輛充電與用戶的使用習慣以及單一車輛的性能有關;宏觀上看，充電負荷受到電動汽車數量、充電設施數量以及氣象等因素影響。目前電動汽車負荷預測主要采用蒙特卡洛法，但其建立在燃油車的統計數據基礎上，沒有考慮電動汽車用戶的個人習慣對于充電負荷的影響。本文從電動私家汽車車主的可能充電的時間段出發，針對一定范圍內的電動汽車，研究日行駛里程、電動汽車用戶充電行為習慣以及充電可能時間等因素對于電動汽車充電負荷的影響，借助隸屬函數描述可能性的功能[1]，建立了描述該區域內電動汽車充電的充電可能性隸屬函數[2]，得到電動汽車充電負荷模型，最終通過獲得充電日負荷曲線。

1? 基于區間數的模糊數學隸屬函數建模

1.1 區間數的構造

電動汽車的停車時間與其充電時間相關，故選取停車時間區間數Tk=[Tk1，Tk2]作為可能充電時間。將其看作正態模糊數的α-水平截集[Tk1，Tk2]。Tka即表示某一時間區間的α-水平截集。將所得n組結果進行處理，得到一組區間數。每組數據權重與時間范圍有關，TX為充電的起止時刻，Tk2-Tk1表示充電時長，將Vk作為權重影響因子[3]則有：

因此，基于電動汽車停車時間的充電時刻區間可用一組新的區間數α-水平截集表示。

1.2 基于區間數的模糊隸屬函數

電動汽車的充電可能性服從隨機概率分布，針對單一充電行為以正態分布表征隸屬函數。通過α-水平截集構建基于區間數的模糊隸屬函數可以得到n個可能充電時間的隸屬函數如公式（4）所示。

其中，x表示時刻，表示充電可能性。由電動汽車充電行為能得到n個充電可能區間如公式（5）所示。

其中，正態模糊隸屬函數的均值為標準差為充電模糊隸屬函數橫坐標為時刻，縱坐標為充電可能性，故該充電時間段內充電可能性曲線如公式（6）所示，

1.3 分段隸屬函數建模

依據隸屬函數二元比較法，充電起始時間的分布將服從以充電峰值時刻為均值，以1為標準差的正態分布，可得到隸屬函數的分段函數如公式（7）所示，其中a為公式2中的區間均值。

1.4 電動汽車充電可能性曲線模型

通過所得到的分段建立的充電可能性曲線可以構成電動汽車充電負荷可能性曲線，用以描述電動汽車充電負荷的變化趨勢。其中，μn表示充電可能性隸屬度，bn為數據權重。充電可能性曲線能夠描述這一天內各個時間點的電動汽車充電可能性大小，其值僅與時間t有關。

1.5 充電負荷模型構建

基于充電量與耗電量動態平衡的假設，可以得到該日電動汽車充電負荷總量Z。通過隸屬函數的方法可以得到電動汽車充電可能性曲線G（t），W（t）表示電動汽車充電負荷，如公式（9）所示。

2? 實例分析

目前某區域內電動汽車600輛，電動汽車的日行駛里程平均68.49km，電動汽車行駛里程效率0.6072百公里耗電量15kWh。按不同通勤里程，區域內電動汽車每2、3、5天充電一次，得到電動汽車的日總充電量為1877.5kWh，區域內電動汽車充電樁功率為3kW。為方便對比分析，針對相同場景，區域內電動汽車早晨、中午、晚上離開與到達時間分布分別服從于N（32，1.2），N（48，0.9），N（78，4.1），N（34，0.9），N（54，0.5）， N（88，6.0）的正態分布，可以得到采用模糊數學隸屬函數與蒙特卡洛方法的充電負荷預測結果。通過比較可知，針對有明顯行為特征的私家車，采用文中方法預測最大充電功率需求為117kW，最小充電功率需求為0kW，采用隸屬函數的方法其預測結果誤差最大值小于5.04%，平均誤差約2.4%。可以證明，本文提出的方法針對電動汽車充電負荷預測較準確。

3? 結語

本文將模糊數學描述不確定性應用于電動汽車充電負荷預測中，針對某一區域，特別是具有復雜用電規律的區域，從區域內電動汽車用戶的電動汽車使用規律出發，對用戶需求進行分析，提出了一種基于隸屬函數的電動汽車充電負荷預測方法。從電動汽車用戶的用車習慣出發，利用隸屬函數描述可能性的性質，建立了基于電動汽車充電可能性的負荷曲線模型。通過與蒙特卡洛法預測結果的對比與誤差分析，驗證了該方法預測結果的準確性，證明了應用模糊數學隸屬函數方法解決電動汽車充電負荷預測問題的可行性。

參考文獻

[1] 洪濤，龔文濤.基于模糊數學的信任度評估方法[J].自動化技術與應用，2020，39（2）：41-44.

[2] 王艷平，王金英，申立平.基于粗糙隸屬函數的強粗糙模糊近似算子[J].數學的實踐與認識，2020，50（3）：245-250.

[3] 趙斌，何涇沙，張伊璇.基于信息熵隸屬度的決策屬性權重確定方法[J].山東大學學報：理學版，2016，51（3）：86-90.