考慮地震風險下的鐵路走向方案決策方法研究

曹 祥

（中國鐵路設計集團有限公司，天津 300301）

我國地處亞歐板塊與太平洋板塊的交界地帶，歷史上曾多次發生重大地震。尤其是我國西南山區震裂帶大量分布，更是地震頻發。重大地震一旦發生，就會對鐵路線路產生廣泛而深遠的破壞。而我國《中長期鐵路網規劃》中，明確未來我國“八縱八橫”高鐵網絡中有一半以上線路將不得不經過地震艱險山區[1]。如此形勢之下，如何在地震風險下選擇一條前期建設和后期運營風險綜合效益最佳的線路，將是設計人員和決策者未來要面對的巨大挑戰。

近年來因汶川地震的巨大破壞力和后續影響，我國許多學者也開始廣泛關注與研究地震山區鐵路選線決策問題，并取得了一些學術成果：朱穎等[2]依據斷裂構造地貌理論與地震波動理論探討了方案走向與空間定線的技術與原則；羅圓等[3]針對川藏鐵路提出利用ALARP準則對地震風險進行分類，并依據分類結果給出了方案風險調控程式。陳蓉淮[4]利用RS和GIS技術對地震山區鐵路災害進行綜合評估，可用于指導選線決策。通過分析學者的研究成果可見，目前學者主要從提高空間選線減災技術和首先單獨判斷地震風險的可容忍度再對方案進行風險調控兩個層面指導選線決策[2-6]，將地震風險納入鐵路選線前后期進行綜合決策評價的研究還相對較少。

為此，文章以力求貼近決策者實際的決策模式為切入點，構建了基于前景理論的鐵路選線決策模型，將不同地震風險狀態納入決策模型中對方案進行綜合評價。因為前景理論所得結果容易受到決策者主觀情感的影響，一些極端指標值可能會決定最終方案的合理性，而VIKOR法能夠中和各指標之間的不相容度，從而得到總體最優妥協解[7]，避免了前景理論的不足。所以文章將前景理論與VIKOR相結合，提出了一種考慮地震風險的鐵路方案優選決策方法用以指導鐵路選線，以提高地震山區鐵路選線質量和水平。

1 云模型

云模型是一種反映現實生活不確定關系的數學理論，其核心是利用期望Ex、熵En和超熵He三個數字特征來表示定性概念。其中，期望Ex表示定性概念的平均水平；熵En反映了定性概念的模糊性；超熵He用來度量云滴的離散程度和確定度，反映了定性概念的隨機性。因此，云模型綜合地考慮了定性概念自身的隨機性和人們對定性語言的模糊認知。相關定義[8]如下：

定義1：設U={x}為一論域，C為可表示定性概念的語言值，若元素x對定性概念C的隸屬度μC（x）是一個具有穩定傾向的隨機數，則稱這種隸屬度μC（x）在論域U上的分布為云，即μC（x）：U→[0,1]，均有x→μC（x）。通常把云模型記為C（Ex,En,He）。

定 義2：設C1（Ex1,En1,He1）和C2（Ex2,En2,He2）為論域U中兩朵一維正態云，根據正態云“3En規則”，正態云C1和C2的Hamming距離為

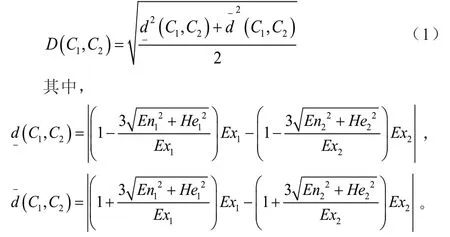
為了使兩朵云C1、C2能夠比較大小，文章引入云模型可能度的概念[9]。論域U中的正理想云為，則P（C1≥C2）為C1≥C2的可能度，計算公式為

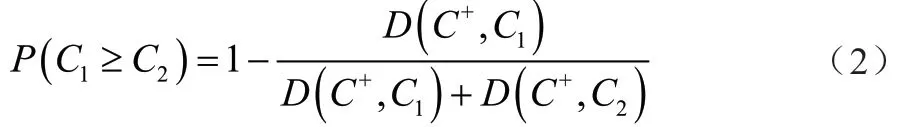
其中，D（C+,C1）和D（C+,C2）分別為C1和C2與理想云C+的Hamming距離。若P（C1≥C2）≥0.5，則C1≥C2，否則C1＜C2。特別指出，若P（C1≥C2）=P（C2≥C1）= 0.5，則云C1=C2。

2 前景理論

前景理論是由Kahneman等學者提出的一種較新的決策理論。它考慮了決策信息的不確定性與決策者自身心理特征在決策過程中的作用，因此更貼近決策者實際的決策行為[10]。前景理論通過方案綜合前景價值V的大小實現各方案排序。而前景價值V由價值函數v和決策權重函數π兩部分共同決定。具體計算公式如下：

其中，價值函數v（x）表示決策者對各項方案屬性心理上的主觀感受價值。決策權重函數π（P）表示決策者對客觀世界外部狀態的主觀感知概率。二者的計算公式如下：

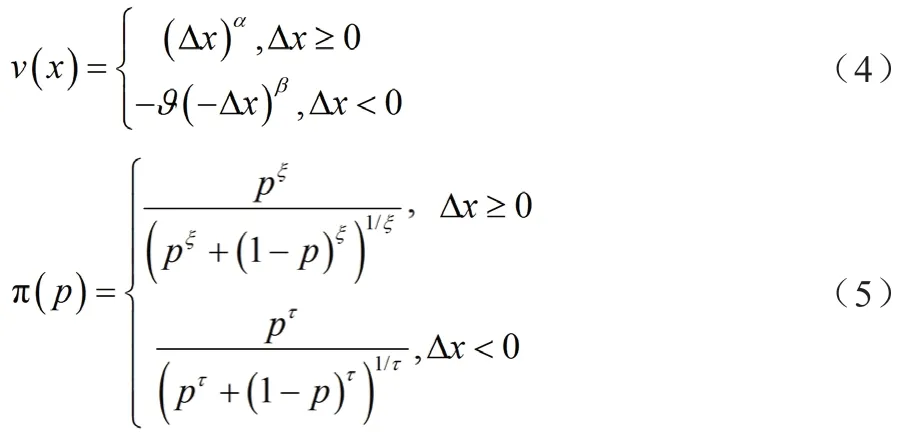
式中：△x為各項方案指標值偏離參考點的距離，表示獲得收益，△x≥0表示遭受損失；α、β分別表示決策者心理上對收益和損失的敏感程度；＞1解釋了現實生活中往往對損失更厭惡的心理特征；P為外部環境狀態的客觀概率；ξ和ι分別為決策者偏好收益與規避風險的心理對外部客觀概率形成主觀決策權重過程中的影響系數。經許多學者研究后，相關參數通常取值為α=β=0.88，=2.25，ξ=0.61，ι=0.69。

3 構建地震風險下鐵路走向方案決策指標體系

地震山區鐵路走向方案優選是一個涉及多因素的復雜性、不確定性、多目標決策問題，需要綜合考慮地形地質地物、土建投資、環境、后期運營、經濟據點、礦藏分布、路網布局等多項因素。文章通過提煉前人的研究成果，以科學、全面、符合實際為原則，從技術、經濟、施工難度、地形地質條件、社會效益五個維度出發，構建了涵蓋技術可行性、經濟合理性、施工條件及環境影響、社會政治經濟意義四個決策指標準則層，見圖1。

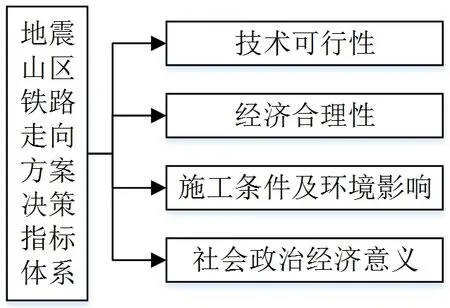
圖1 地震山區鐵路走向方案決策指標體系

為了全面反映地震山區鐵路選線因素的影響，以提高線路決策結果的有效性，需對每項指標層涉及的主要因素進行界定。值得注意的是，地震山區的地震因素影響突出，因此決策過程中除了考慮非地震山區一般鐵路選線影響因素，還需考慮地震因素對各類決策指標層的影響。技術可行性指標層主要考慮線路長度、橋隧總長、征地拆遷量、土石方量、地質條件、地震動峰值加速度、地震因素對線路各類構造物設計標準的影響以及各類抗震措施的設置技術等因素；經濟合理性指標層主要考慮工程投資、運營費用、機車購置費用、后期地震因素造成的線路各類構造物的震害損失以及運營中斷導致的運營收益損失、地震因素導致的后期修繕維修費用等因素；施工條件及環境影響指標層主要考慮地形地質條件以及抗震設計帶來的施工難度、工程建設與地震因素的相互作用對生態環境造成的影響等因素；社會政治經濟意義指標層主要考慮線路帶動周邊地區經濟發展與滿足地方需求的能力、改善路網與城市規劃布局方面的積極意義、后期地震因素導致線路中斷運營帶來的社會政治經濟方面的影響、地震因素對社會各方對線路應急救援管理難度的影響等因素。

4 基于前景理論和云模型的鐵路線路方案決策方法

4.1 問題描述

在地震山區鐵路線路優選方法問題中，假定有待選的鐵路線路方案集A=｛A1,A2,…,Am｝，其中Ai表示第i個鐵路線路方案；線路方案的決策指標集合為U=｛U1,U2,…,Un｝，其中uj表示第j個指標；x=（x1,x2,…,xk）為鐵路線路行經區域未來一定時期內可能發生的地震等級類型，其中xt表示第t種地震狀態；ω=（ω1,ω2,…,ωj）表示對應決策指標的權重，其中ωj表示決策指標Cj的權重，顯然應滿足0≤ωj≤1，；S=｛VG,G,SG,F,SP,P,VP｝=｛很好，好，較好，一般，較差，差，很差｝為決策者對線路方案指標的不確定語言評價集。

為綜合反映定性概念自身的隨機性和人們對定性語言的模糊認知，利用云模型將不確定語言評價值定量化。文章引用文獻中云模型與不確定語言評價集的轉化關系見表1。

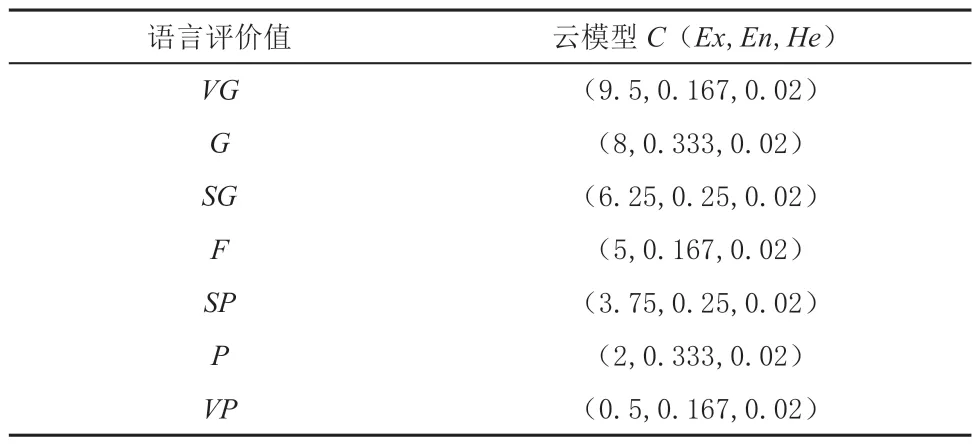
表1 云模型與定性語言評價值的轉化關系

因此文章研究的主要問題是決策者分別對各種地震狀態下各線路方案決策指標做出評價，選取適當參考點，并確定決策指標權重，最后利用前景理論和VIKOR方法選出最優線路走向方案。

4.2 確定參考點

參考點是決策者心理上判斷收益和損失的潛在基準，并與決策者自身的從業經驗、性格偏好等因素有關。為了分擔每個決策者單一參考點下選擇不當的風險，盡可能綜合多名決策者信息，文章構建不同地震狀態xt下的正理想方案云、負理想方案云、平均期望方案云三個參考點。

正理想方案云：

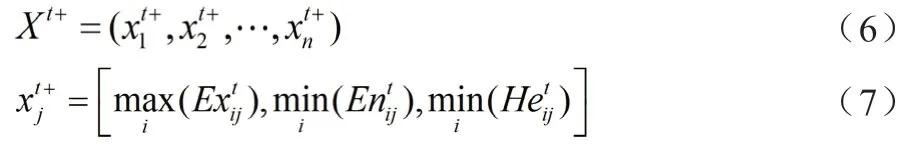
負理想方案云：

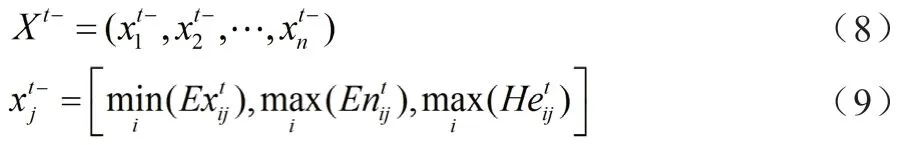
平均期望云方案云：

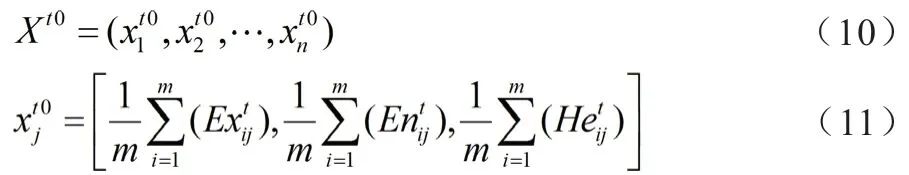
4.3 確定價值函數

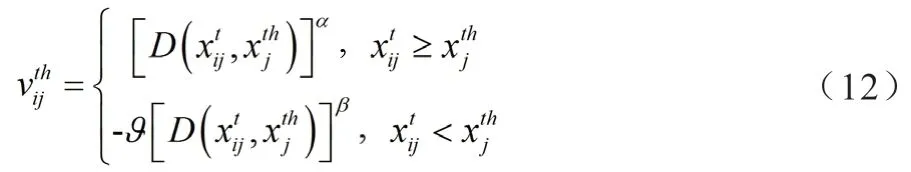
4.4 確定決策權重

決策者的決策權重與決策者的風險態度和地震發生狀態的客觀概率有關。為了綜合考慮地震活動的周期性和隨機性，文章引入布朗（BPT）-泊松（poi）聯合概率模型[3]對地震狀態xt發生的客觀概率進行預測。計算公式如下：

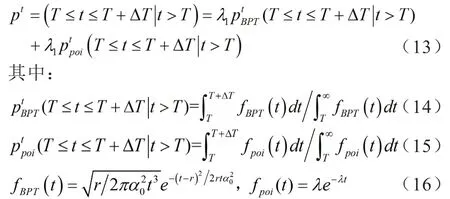
式中：Pt表示地震狀態xt發生的概率；r為斷裂帶的平均復發間隔；λ表示破裂的年發生率，λ=1/r；α0是變異系數，通常取值為0.5；T表示最近一次地震狀態xt發生到目前的時間；△T表示新建鐵路的服務期，本文取值為△T=100年。λ1、λ2表示地震活動周期性和隨機性的組合系數，若地震活動周期性和隨機性無明顯差異，可取λ1=λ2=0.5。

通過上述確定地震狀態xt發生的客觀概率Pt后，采用式（5）即可確定地震狀態xt下各線路走向方案的決策權重πt（p）。

4.5 確定三參照點下各決策指標的綜合前景價值

依據前景理論，可分別計算基于第h個參考點方案在地震狀態xt下線路走向方案Ai對應的決策指標uj的前景云價值。計算公式如下：

文章通過設計問卷、專家咨詢等手段對相關單位決策群體中潛在參考點的分布情況做深入調查，分別確定決策群體中正理想方案云、負理想方案云、平均期望方案云三個參考點的偏好權重，滿足。并通過參考點偏好權重對進行集結，確定基于三參照點在地震狀態xt下線路走向方案Ai決策指標uj的綜合前景云價值。計算公式如下：

4.6 基于前景理論的綜合決策優選方法

鐵路線路走向方案決策是一個涉及設計院、政府、相關鐵路單位等多方部門共同協商的決策過程。各方代表自己的意見通常有不同的決策準則，而VIKOR方法正是一種用于解決多準則問題的妥協排序決策方法[14]。它的基本原理是通過各決策準則讓步而獲得離理想解最近的妥協解。因此，文章通過引入VIKOR方法與前景理論相結合對線路走向方案進行決策排序。具體決策步驟如下：

（1）首先確定各決策指標的重要度，即指標權重ω=（ω1,ω2,…,ωj）。為充分吸收決策者的主觀經驗同時兼顧決策數據本身的信息，文章在決策者主觀給出部分指標權重信息的基礎上，依據離差最大化方法[15]構建一種線性規劃優化模型，即

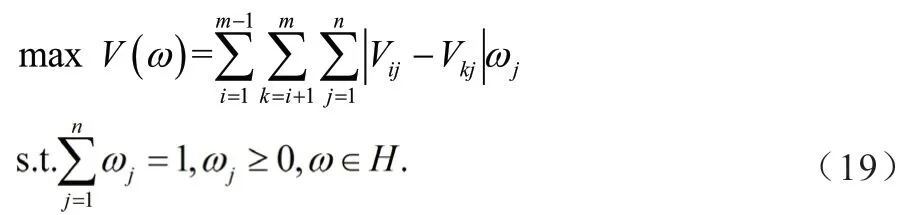
其中，H為由決策者主觀給出的部分決策指標權重信息。利用Matlab或者Lingo編程求解模型可獲得決策指標最優權重向量ω=（ω1,ω2,…,ωj）。

（2）確定各線路走向方案綜合前景云價值的正理想解f+和負理想解f-。通過4.2～4.5可得到地震狀態xt下線路走向方案Ai決策指標uj的綜合前景云價值。在此基礎上分別定義f+、f-如下：

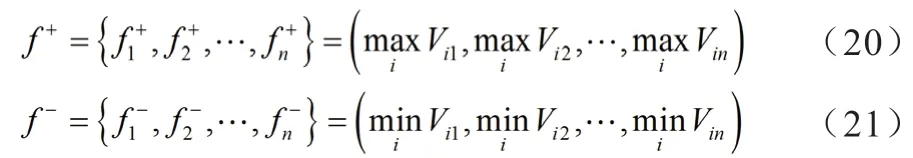
（3）確定各線路走向方案的群體效益值Si和個體遺憾度Ri，其中i=1,2,···,m。

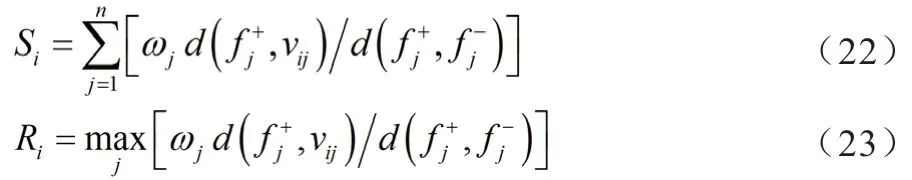
（4）確定各線路走向方案的折中排序值Qi。其中i=1,2,···,m。

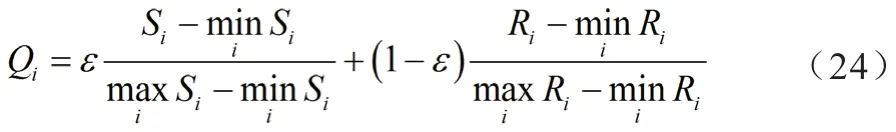
其中，ε∈[0,1]是決策妥協系數，文章取ε=0.5，表示決策結果由各方共同協商確定。

（5）確定最優方案。首先依據Si、Ri、Qi從小到大對各項線路走向方案進行排序，線路走向方案排序越靠前，則方案越優。若滿足以下兩個決策準則，則Qi值最小的方案為最優方案。

①可接受優勢準則：Q（A2）-Q（A1）≥1/（m-1），其中，A1和A2分別為Q值最小和次最小線路走向方案，m為待選線路走向方案個數。

②可接受穩定準則：A1在所有線路走向方案中Si或Ri最優。

若不滿足準則①，則A1,A2,…,AM均為總體妥協最優方案，M由Q（A2）-Q（A1）＜1/（m-1）確定；若不滿足準則②，則A1和A2構成妥協最優方案集。

5 案例分析

文章選取地震山區某新建鐵路雅安至瀘定段線路走向方案優選作為工程實例進行決策研究，驗證文章所建模型的科學性與適用性。

該段鐵路地形地質條件復雜，構造運動頻繁，地震頻發，氣候條件惡劣，會對雅安及其周邊地區造成嚴重破壞，因此該段線路走向的選擇對與鐵路建設和后期的運營維護都具有重大意義。經設計院研究主要形成經天全方案A1和經滎經方案A2兩個方案。其中，經天全方案A1為最終確定方案。我國目前《鐵路工程抗震設計規范》只適應于地震峰值加速度0.4g，相當于地震烈度為9度弱的情況。然而，歷史上超標準地震是存在的，如唐山、汶川地震烈度均超過了11度。因此文章結合我國新建線路服務壽命通常為100年，假定線路自完工至未來100年內可能面臨三種地震狀態：（1）大地震（烈度10度及以上，并造成鐵路大范圍內嚴重震害）x1；（2）中小地震（烈度小于10度，震害中等，并可通過加強抗震設計、措施進行防控）x2；（3）不發生地震x3。從技術可行性（C1）、經濟合理性（C2）、施工條件及環境影響（C3）、社會政治經濟意義（C4）指標層出發，給出決策者針對每個地震狀態xt、每個線路走向方案Ai的不確定語言評價值，并依據表1將不確定語言評價值轉化為云模型評價值，詳見表2。

表2 不同地震狀態下各線路走向方案指標的云模型評價信息表

其次，依據表2中各方案指標的云模型評價值和式（6）～式（11）計算三種地震狀態下各線路走向方案的參考點方案評價值，結果見表3。

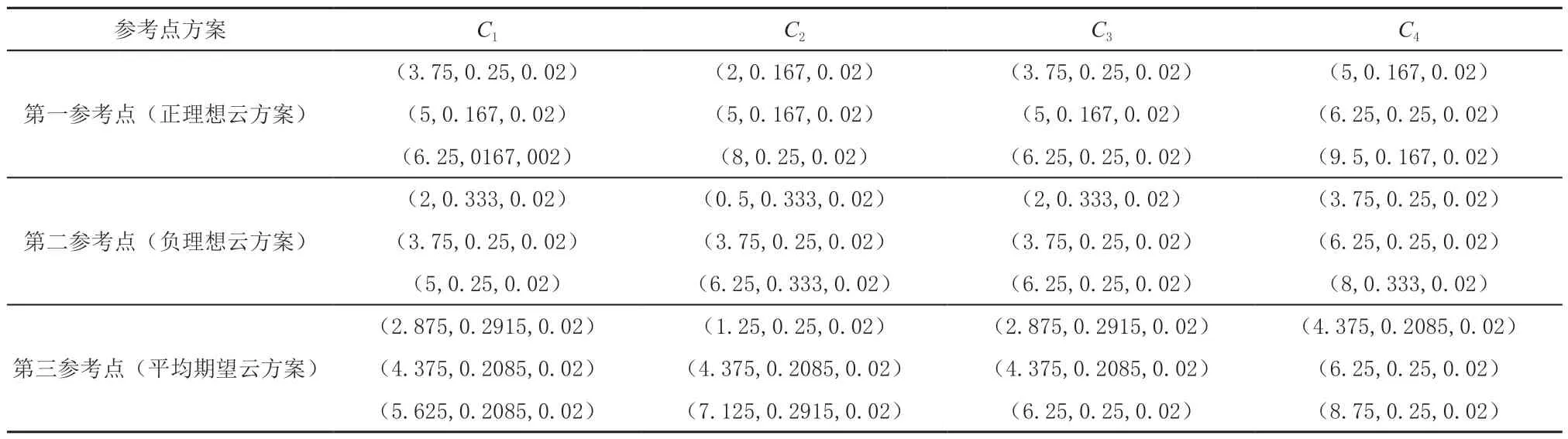
表3 不同地震狀態下的參考點方案評價值

然后確定不同參考點下各線路走向方案指標的前景價值。三種地震狀態發生的客觀概率Pt（P1,P2,P3）。根據文獻中的研究，未來地震狀態x1時，取平均值r=500年，T=6年；未來地震狀態x2時，取平均值r=161年，T=40年。依據模型（10），利用Matlab數值積分計算可求得地震狀態x1、x2發生概率的近似值P1=0.1194，P2=0.4592，則地震狀態x3的概率P3=1-P1-P2=0.4214。依據不同地震狀態的客觀概率Pt、表3中不同地震狀態下的各參考點方案的評價值和式（3）、式（5）、式（12）、式（18）計算三個參考點下各線路走向方案指標的前景值，計算結果見表4。

接著，依據式（12）對三個參考點下各線路走向方案指標的前景價值進行加權融合，決策群體中各參考點的分布比例情況確定為（0.3,0.3,0.4），得到各線路走向方案指標三個參考點的融合前景值見表5。

隨后，依據離差最大化思想，并結合決策者給出的部分指標權重信息，用式（13）構建如下權重優化模型：

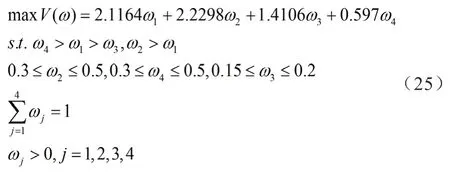
利用Matlab編程對模型進行編程求解，得到指標最優權重：ω1=0.15，ω2=0.4，ω3=0.15，ω4=0.3。

最后，依據表5中各方案指標的融合前景值與方案指標最優權重，利用VIKOR方法確定最優線路走向方案。通過式（14）～式（18）得到計算的結果見表6。

根據表6的計算結果，結合VIKOR的最優方案的判定準則，顯然有Q1＜Q2且線路走向方案A1同時滿足準則①和準則②，因此線路走向中經天全方案A1為最優方案。

在實際決策過程中，決策者對群體效益和個體遺憾可能會有不同的決策態度，進而會影響到決策結果。因此，為了驗證最優方案的穩定性，文章將決策妥協系數ε∈[0,1]以0.1為步長進行取值，探討決策者采取不同決策態度時最優方案的變化情況。計算結果見表7。

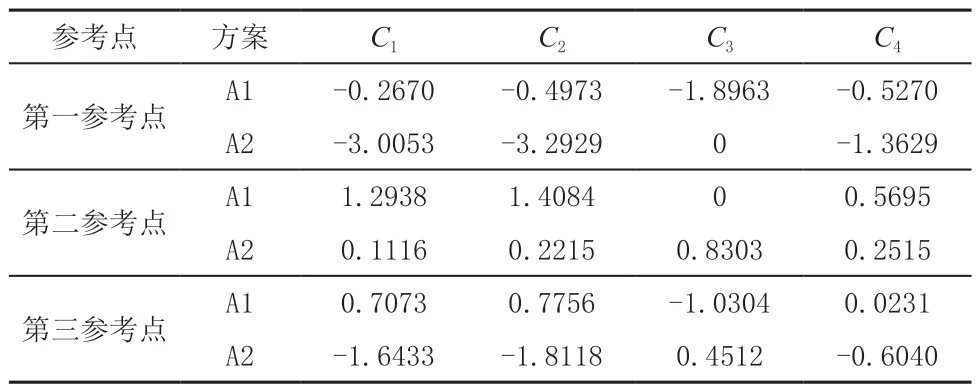
表4 不同參考點下各方案指標的前景值計算表

表5 三參考點下各方案指標的融合前景值計算表

表6 各線路走向方案的Si、Ri以及Qi

依據表7中的計算結果與VIKOR的判定準則，可得到決策者采取不同決策態度時線路走向方案的排序情況，見圖2。

表7 各線路走向方案的Si、Ri以及不同決策態度ε下的Qi值

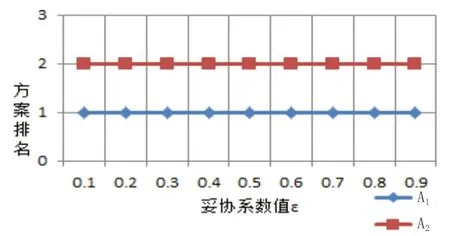
圖2 不同決策態度下方案排序結果

隨著決策妥協系數的變化，決策者從看重個體遺憾逐漸向更多考慮群體效益傾斜，從圖2可以看出，最優方案均為A1，說明了最優方案是穩定的。文章所得最優方案與設計院最終確定的方案是一致的，驗證了上述決策方法的科學性與可靠性。

6 結論

（1）在地震頻發山區進行鐵路選線時，如何綜合平衡后期地震風險與線路建設的技術、經濟及社會效益之間的關系，將是設計人員和決策者面臨的難題。為此，文章基于前景理論將未來地震風險納入線路優選決策模型中，將未來地震風險劃分為不同的情景狀態，在不同地震狀態下對各線路方案進行評價，并依據未來地震狀態發生概率、前景理論與VIKOR方法對各方案實現綜合優選。這為地震山區鐵路選線決策提供了一種新的思路。

（2）決策過程中，利用云模型表示決策者對線路走向方案的評價值，綜合了人類思維模式的隨機性和模糊性，能良好反映決策者思維和鐵路選線決策系統的不確定性；利用前景理論確定線路方案前景價值過程中，綜合考慮了決策者對地震狀態客觀概率的主觀感知與對線路方案屬性損失或收益的敏感程度，這更貼近決策者實際的決策模式；依據各線路方案屬性前景價值利用VIKOR實現綜合優選，兼顧了多方部門的群體效益與個體遺憾，使決策結果具有更高的穩定性。

（3）決策模型中利用布朗-泊松聯合概率模型預測不同地震風險狀態概率，充分考慮了地震活動的隨機性與周期性；依據離差最大化思想與專家給出的部分權重信息，利用數學規劃確定線路方案指標最優權重，綜合考慮了專家經驗與各線路方案指標值的差異性，使指標權重更加合理；綜合各線路方案屬性正理想云、負理想云、平均期望云三參考點進行決策，照顧了不同決策群體的心理特點，避免了特定類型決策者單一參考點下選擇不當的風險，提高了決策的科學性。