基于STARMA模型的濟寧城市內澇模擬分析
舒博寧,趙曉旭,李曉霜
(濟寧市水文局,山東 濟寧 272019)
近年來,極端氣候不斷出現,導致暴雨多發、城市內澇問題突出,嚴重威脅城市市民的生命財產安全[1]。濟寧市水文局針對城市的水文情況展開研究探討,牽頭西安山脈科技股份有限公司等單位開發了“濟寧市城市水文監測系統”。其中,針對城市內澇問題,引入STARMA模型,建立城市內澇模擬系統。該模型對濟寧市城市內澇模擬效果較好,有助于洪澇災害的防控,可有效提高城市的信息預警能力。本文將STARMA模型創新性的應用于濟寧市區的內澇模擬與風險評估中,根據降雨量對城市內澇進行及時的評估,提高抗風險的能力。
1 時空自相關移動平均模型
該模型是在自相關移動平均模型(ARMA)的基礎上,考慮了空間上鄰近點的影響[2]。將時空變量定義為空間上有相關關系的時間序列集合,研究時空變量和時間、空間的關系。時空變量的主要特征為時空相關性和時空異質性是其最主要的特征。其中,空間相關性由空間鄰接矩陣進行描述。STARMA模型的zi(t)的值受到該點的過去時刻值、過去擾動值、空間鄰近點的過去時刻值和過去擾動值的影響。STARMA模型的建模流程主要有模型識別、參數估計和模型檢驗。
2 內澇積水時空序列模型STARMA建模
將STARMA模型應用于城市的內澇積水預測建模過程如下:內澇積水時間序列數據→數據預處理→數據平穩化→空間鄰接矩陣→計算時空自相關和偏相關函數,選擇合適模型→模型參數估計→模型驗證與預測。
2.1 數據采集及預處理
濟寧市內澇積水監測網共有9個內澇積水監測點和9個雨量站點,均分布在濟寧市城區內,表1顯示的是濟寧市低洼地水深監測站站點分布。表2顯示濟寧市雨量站點一覽表。本文以濟寧市2018年某月內澇積水過程為研究對象,以太白湖區的1個積水監測點的內澇積水數據為基礎進行STARMA建模與預測。內澇積水數據采集過程如下:記錄每隔3min的降雨總量及每隔6min的積水高度,精度為1mm,采用線性插值法將補足缺失的數據。

表1 濟寧市低洼地水深監測站站點分布
2.2 數據平穩化
STARMA模型適用于時間空間均離散的平穩時空序列。然而,內澇積水時空監測序列在地理學中屬于空間連續時間離散的時空序列,其在時間上是弱的平穩序列。因此,這樣采集到的內澇降水數據并不能直接輸入模型,而需要進行平穩化處理。在此,采用BP神經網絡對采集的數據進行平穩化處理[3]。
2.3 內澇積水空間鄰接矩陣
內澇積水的預測研究中,降雨量是一個重要的考量對象。而在實際的規劃中,雨量站和積水站一般分布在城區的不同位置。本通過空間差值法,計算積水點的降雨量。根據雨量站和積水站距離的函數來建立積水對應雨量站的空間權重矩陣。
2.4 模型識別
在計算STARMA模型時,通過計算時空自相關和偏相關函數來確定模型的階數和,選擇ARMA(1,1)為合適模型。同時,由于階數p和q需要其他統計量來輔助判斷。本文采用選擇均方根誤差RMSE擬合優度R2、平均絕對誤差MAE輔助計算模型的階數。
2.5 參數確定
根據已經建立的空間鄰接矩陣和模型識別的結果,將時空自相關移動平均模型應用于定量太白湖區的內澇積水,可以確定該內澇積水的時空自相關模型 STARMA(1,1)為:
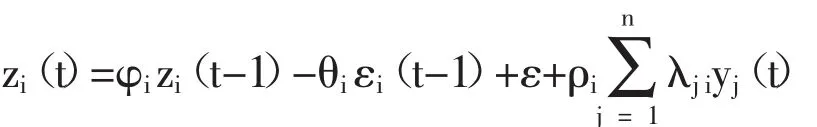
式中:yj(t)是雨量j站點t時刻的降雨量,n為受影響的雨量站點個數。
提取一次歷史的降雨積水數據,選擇最小二乘用于參數的估計,并對模型進行顯著性檢驗,經計算:太白湖區F值為70.8326,R2值為0.9815,MAE值為0.0125。其中,F檢驗是顯著性檢驗,F越大說明方程越顯著;R2是模型的擬合優度,R2越接近于1,說明模型擬合效果越好;MAE越小說明模型越精確。參數估計值經計算:φi值為0.9768,θi值為 0.7546,ε 值為 1.2384,ρi值為0.0055。
2.6 STARMA模型準確度評價
根據在濟寧太白湖區采集的步長為6min的內澇積水對建立的STARMA模型的預測性能進行進行評價。相對平方誤差RSE、方根誤差RMSE和相對誤差比率RE被應用于不同時間評價結果的準確度測量,經計算:太白湖區6min RSE 值為 0.0281,RMSE 值為 0.0087,RE 值為2.3;12minRSE值為 0.0258,RMSE 值為0.0112,RE值為2.45;18minRSE值為0.0273,RMSE值為0.0136,RE值為2.86。從結果可以看出,建立的模型STARMA的預測準確度較高。但是,隨著預測時間的增加,模型的預測精度稍微下降。太白湖的內澇積水時間跨度較長,歷時4h,預測精度誤差在3%左右。
3 結語
本研究是針對濟寧市的暴雨積水數據提出的內澇積水預測系統,是濟寧市水文局開發的“濟寧市城市水文監測系統”的重要組成部分。該系統通過采集濟寧市區的實時降雨和積水數據,達到對城市內澇實時監控的目的。
雖然該系統的預測準確率較高,但是由于除了降雨和積水外,內澇積水還受到排水等情況的影響。因此,模型的可靠性還需要了進一步的完善,以保證該系統能夠反映最真實的積水情況,提高系統的真實性和可靠性。

