數(shù)值模擬激發(fā)條件對賓川水庫氣槍信號振幅的影響

孫楠 孫耀充

摘要：利用有限差分方法，對賓川氣槍試驗中激發(fā)條件對氣槍信號振幅的影響進行數(shù)值模擬。結果顯示：水庫水位對信號振幅的影響呈非線性關系，34 m為氣槍激發(fā)試驗的優(yōu)勢激發(fā)水位，能產生最強波形振幅能量，而水位變化的影響隨距離緩慢減小。通過擬合給出了不同水位變化幅度與其產生的平均振幅變化率之間的冪函數(shù)關系，可為實際波形運用中去除水位變化的影響提供理論參考。波形振幅與激發(fā)能量及震源沉放深度呈近線性關系，即激發(fā)能量越大，震源沉放深度越深，氣槍激發(fā)效果越好，越有利于進行遠距離深穿透地下結構的探測。

關鍵詞：數(shù)值模擬;水位;沉放深度;激發(fā)能量;信號振幅

中圖分類號：P315.6文獻標識碼：A文章編號：1000-0666（2020）04-0711-09

0引言

水庫大容量非調制氣槍陣列震源是通過在水中瞬間釋放槍體中高壓氣體產生地震信號，具有激發(fā)效果好，可控性、操作性強的優(yōu)勢（Reasenberg，Aki，1974;陳颙等，2007，2017;陳颙，李宜晉，2007;羅桂純等，2006），是進行區(qū)域尺度深部結構探測的理想人工震源（Chen et al，2008;林建民等，2008;王偉濤等，2017）。利用氣槍震源高度重復性及具有較高能量的特性可以動態(tài)監(jiān)測區(qū)域波速變化（王寶善等，2011;Wang et al，2020），對地震預測研究具有重要意義。2012年云南賓川建成了全球首個陸地激發(fā)氣槍震源發(fā)射臺，隨后在新疆呼圖壁、甘肅張掖等地也建設了固定式氣槍震源發(fā)射臺，進行連續(xù)激發(fā)或密集臺陣觀測試驗（王彬等，2016;魏斌等，2016;張元生等，2016），還在福建發(fā)展了船載式和移動式氣槍震源系統(tǒng)，在長江安徽段開展了氣槍震源流動激發(fā)試驗，為區(qū)域尺度的地殼結構探測研究提供了有力工具（姚道平等，2016;徐逸鶴等，2016;王寶善等，2016）。

在陸地水庫中進行氣槍震源試驗時，由于水深較淺、水域面積有限，氣槍震源激發(fā)過程實為氣槍源與淺水區(qū)相互作用的過程，共同構成淺水區(qū)氣槍震源激發(fā)系統(tǒng)。近年來，很多研究表明，在淺水環(huán)境中激發(fā)產生的地震波會受到氣槍源本身配置（氣槍的容量、激發(fā)壓力等）以及外部激發(fā)環(huán)境的影響，如氣槍所在水庫的水位變化、氣槍震源的沉放深度等（Chen et al，2014）。Dragoset（2000）通過研究氣槍震源激發(fā)信號特征，給出了激發(fā)信號與氣槍容量、工作壓力和沉放深度等激發(fā)參數(shù)之間的具體關系及經(jīng)驗公式;唐杰等（2009）和林建民等（2010）均對2007年9月上關湖水庫氣槍激發(fā)試驗中水聽器記錄的近場波形數(shù)據(jù)進行模擬和分析，發(fā)現(xiàn)氣槍震源沉放深度、工作壓力等不同激發(fā)條件對壓力脈沖和氣泡脈沖存在一定影響;陳蒙（2014）基于賓川多次氣槍試驗，分析了不同激發(fā)壓力、沉放深度和水庫水位等因素對賓川氣槍激發(fā)地震波的影響，發(fā)現(xiàn)水庫水位變化的影響遠遠大于震源沉放深度的影響;孫楠等（2017），Sun和Sun（2019）用雷克子波震源時間進行數(shù)值模擬，發(fā)現(xiàn)水庫水位深度對波形振幅的影響是非線性的，激發(fā)能量和沉放深度與波形振幅近似呈線性關系;胡久鵬等（2017）模擬不同水體形狀對氣槍激發(fā)波形的影響，發(fā)現(xiàn)水體形狀對高頻信號成分影響較強，對低頻信號成分影響較弱。以上研究主要借助數(shù)值模擬方法，分析陸地水庫氣槍震源試驗中不同激發(fā)條件的影響，可以此作為一種輔助手段為實際波形的分析應用提供依據(jù)。

水庫激發(fā)氣槍信號中，最大振幅是氣槍信號的一個重要參數(shù)。在研究氣槍震源對環(huán)境的破壞作用以及對水中生物的影響時，尤其是當氣槍在淺水環(huán)境下激發(fā)時，對氣槍激發(fā)信號最大振幅的研究具有重要的意義（林建民等，2010）。本文主要模擬有限水體中水位、激發(fā)能量、震源沉放深度等激發(fā)條件，對氣槍信號最大振幅的影響特征，從而為水庫激發(fā)氣槍震源工作研究提供理論依據(jù)，這對于進一步深化氣槍震源的應用意義重大。

1數(shù)值模擬激發(fā)條件的影響

有限差分方法作為一種能夠模擬地震波在復雜介質中傳播的數(shù)值計算方法，將區(qū)域網(wǎng)格化，把網(wǎng)格點上的時、空數(shù)值用差商近似為偏微分項，將連續(xù)的偏微分方程轉化成離散格點上值的差分方程。該方法具有簡單直接、計算效率高的優(yōu)點，能比較完善地解決地震勘探、強地面運動預測等研究中地球內部任意非均勻介質問題，準確高效地模擬符合真實地質條件的復雜地形的地震波傳播（Zhang，Chen，2006;Sun et al，2017）。本文將利用有限差分方法數(shù)值模擬激發(fā)條件對氣槍信號振幅的影響。

地震研究43卷第4期孫楠等：數(shù)值模擬激發(fā)條件對賓川水庫氣槍信號振幅的影響本文有限差分法采用同位網(wǎng)格的DRP/opt MacCormack差分格式，將MacCormack格式和DRP（Dispersion Relation Preserving）格式相結合，需要4個網(wǎng)格點的長度，具有4階空間精度且網(wǎng)格分辨率高，通過前后各3個相鄰點差分引入高頻耗散，不僅可以消除奇偶失聯(lián)現(xiàn)象，還可以獲得中心差分的截斷誤差精度，從而正確地計算各項異性介質中地震波的傳播過程（MacCormack，1969;Hixon，1997;Zhang et al，2012;Sun et al，2016），再結合體貼網(wǎng)格技術可以準確描述固液界面的起伏。在計算區(qū)域邊界附近的網(wǎng)格點時，由于沒有足夠的相鄰的計算格點，采用4階空間精度的緊致MacCormack差分格式，結合牽引力鏡像法（Zhang，Chen，2006）實施自由表面邊界條件，在邊界處計算應力分量和速度分量的空間導數(shù)。在計算區(qū)域的左右邊界附近設定一定寬度的吸收層，使用簡單穩(wěn)定易于實現(xiàn)的指數(shù)衰減吸收層，在吸收層內將地震波場和波場衰減項相乘（Cerjan et al，1985），從而達到吸收波場的目的。

1.1介質模型

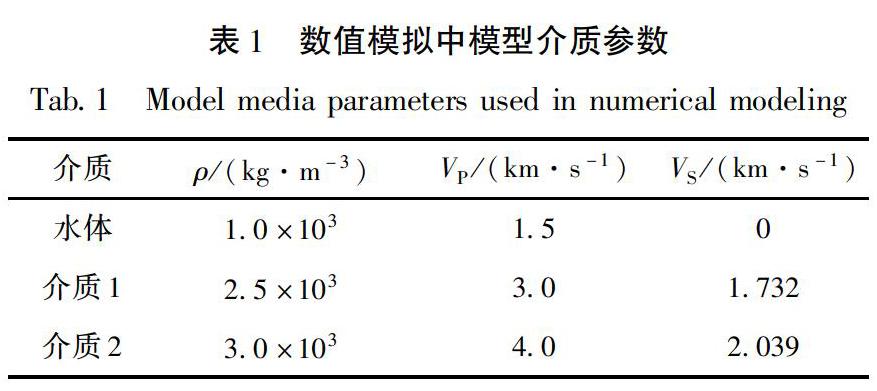
數(shù)值模擬中，研究區(qū)域為4 km×0.6 km大小的層狀半空間介質（圖1），水體位于距左側邊界0.25 km處的第一層，水體形狀使用Gaussian函數(shù)z=b0exp[-（x-x0）2/a20]獲得，水體的第二、三層均為固體介質。模擬中只考慮了彈性情況的幾何擴散的衰減，未考慮非彈性的衰減，具體介質參數(shù)配置見表1。

將震源沉放于水體中，在距離水面10 m處，模擬水庫中氣槍震源沉放方式。在計算區(qū)域的地表面（0.35～4.0 km）設置一條測線，共放置92個檢波器，用于研究激發(fā)條件變化對波形振幅的影響程度范圍。在區(qū)域邊界使用10層的指數(shù)衰減吸收層來吸收向外傳播的波（圖1）。

模擬時首先對區(qū)域進行網(wǎng)格化，網(wǎng)格大小設置為1 m×1 m，共2.4×106個網(wǎng)格，時間步長設置為0.1 ms，能夠滿足二維DRP/opt MacCormack格式的穩(wěn)定性條件要求為：

t<0.93×h/Cmax（1）

式中：h是空間網(wǎng)格間隔;Cmax是介質的最大波速;模擬時間長度總共為3 s，并行計算共占用60個核。對于模擬中震源時間函數(shù)的設置，考慮到水庫作為有限水體，在其內部激發(fā)氣槍信號后會產生氣泡振蕩，而氣泡振蕩的傳播可能會受到有限水體邊界的影響，使得向外傳播的可能為氣泡、水體與水庫邊界的耦合源，其震源時間函數(shù)尚不能明確。而在賓川氣槍震源波形數(shù)據(jù)應用中，通常用發(fā)射臺附近的參考臺波形近似成源，進行反褶積運算，以此來消除由震源變化引起的影響（翟秋實等，2016）。因此，本文選取賓川氣槍發(fā)射臺附近的參考臺波形，用其垂直向最大振幅進行歸一化后的波形形態(tài)，近似成震源時間函數(shù)進行數(shù)值模擬計算，其中歸一化后的垂直向最大振幅約為水平向最大振幅的1.4倍（圖2）。

1.2數(shù)值模擬結果

利用有限差分方法，模擬得到有限水體中不同水位、激發(fā)能量、震源沉放深度等激發(fā)條件時的波形信號，分析其最大振幅的變化特征，從而探究淺水環(huán)境下激發(fā)條件的影響。結果分析中，引用波形的最大振幅的相對變化率（以下簡稱 “振幅變化率”），表征激發(fā)條件變化時波形最大振幅的變化。

從距離震源1 km的檢波器記錄的波形可以看出（圖3），x分量體波和面波的到時均比z分量的早，即在水平向傳播速度更快。x分量的P波振幅比z分量的要大，而z分量的S波和面波振幅則更大。最大振幅分布在面波段，z分量的最大振幅約為x分量的1.4倍。從所有檢波器接收的波形隨距離的分布圖（圖4）可以看出，在不同距離均可以看到非常明顯的面波，最大振幅分布在面波段，z分量的振幅比x分量大。

1.2.1水體水位

賓川氣槍試驗選取大銀甸水庫作為激發(fā)水體，其水位有顯著的季節(jié)性變化（王彬等，2016）。

數(shù)值模擬中，水體形狀使用Gaussian函數(shù)獲得，水平面與地表面持平，保持震源到水面的距離為10 m不變，保持水平面寬度200 m不變，通過增加水庫的深度引起水位的變化（圖5）。

數(shù)值模擬水位范圍為13～40 m，分別選取到水庫右側的距離Δ=0.5，1.0，2.0，3.0 km的4個接收臺站，模擬波形最大振幅隨水位的變化，如圖6所示，4個臺站接收到的波形最大振幅隨水位增加的變化均是非線性的，水平向和垂直向變化形態(tài)大致相同，垂直向最大振幅約為水平向最大振幅的1.4倍，這應該與所選取的震源時間函數(shù)的振幅最大值有關。Δ的增加，表示臺站和水庫距離變遠，從圖6縱坐標的振幅范圍可以發(fā)現(xiàn)，最大振幅的整體變化形態(tài)減小，表明隨著震中距增大，水位變化的影響逐漸減小。

由于各個臺最大振幅隨水位的變化形態(tài)大致相同，對模擬得到的90個臺的波形最大振幅求平均，得到不同水位對應的平靜最大振幅的變化特征（圖7）。從圖7可知，在水位約為13～15 m時，振幅隨水位增加而減小，呈負相關;水位為17～19 m時，振幅隨水位增加而增加，呈正相關;水位為20～24 m時，呈負相關;水位為25～34 m時，呈正相關;水位為35～40 m時，呈負相關，水位約為33 m時波形振幅最大，即振幅激發(fā)能量最強，為優(yōu)勢激發(fā)水位。

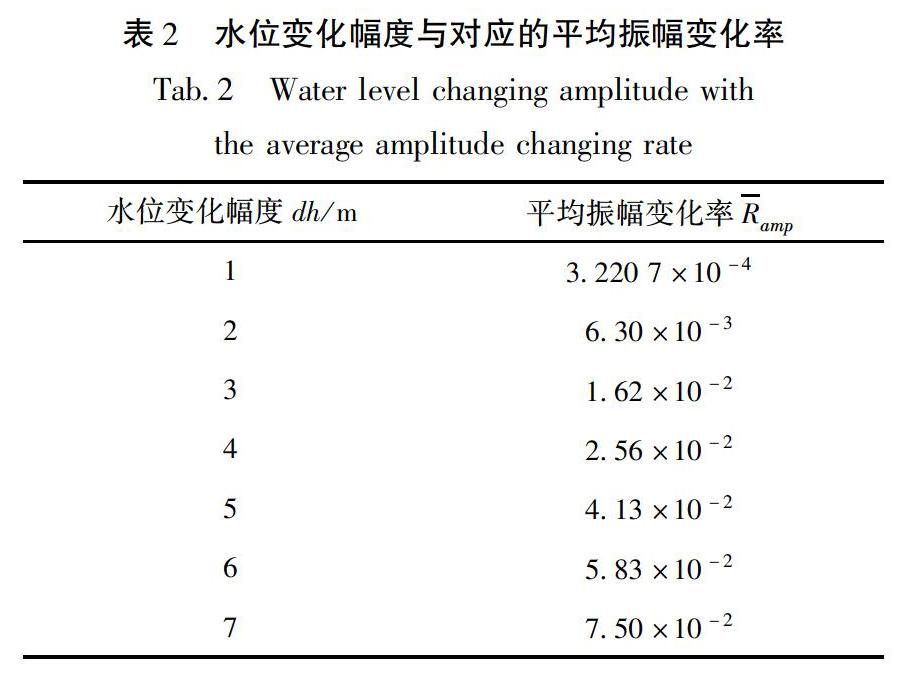
當水位增加1 m時（圖8），不同距離的波形的最大振幅變化顯示，在震中距小于2 km范圍內振幅變化率呈周期振蕩，隨著震中距的繼續(xù)增加，周期振蕩形式逐漸消失。這種周期性振蕩可能與水體振蕩產生的駐波向外傳播的影響有關，隨著震中距的增加，駐波效應也逐漸消失。水平分量的變化稍大于垂直分量的變化，表明水位變化對水平向的影響大于垂直向。水位增加1～7 m時，90個臺站接收的波形振幅變化率顯示（圖9）：水位變化幅度越大，波形振幅的變化率越大。在2 km范圍內，振幅變化率隨距離呈周期性振蕩，也就是駐波振蕩效應的影響范圍約為水面寬度10倍的距離，也使得在某些距離處（如波谷處）接收到的波形受水位變化的影響特別小。將水位變化分別為1～7 m時所有臺站的振幅變化率進行平均，得到由水位變化引起的平均振幅變化率幅度（表2）。由表2可知，當水位增加1 m時，引起振幅變化率約為3.220 7×10-4。擬合水位變化幅度（dh）與平均振幅變化率（Ramp），得到：Ramp=a·dhb（2）式中：a=1.985×10-3;b=1.874;擬合函數(shù)確定系數(shù)Rsquare=0.998 1，非常接近于1，表明擬合效果非常好，平均振幅變化率與水位變化幅度呈冪函數(shù)關系（圖10）。

1.2.2激發(fā)能量

在大容量氣槍試驗中，氣槍震源的激發(fā)能量來源于高壓氣體，可通過Ronen（2002）方程從高壓氣體的容量和壓力計算得出，其具體關系為：E=P·Vln（P/P0）（3）式中：E為氣槍激發(fā)能量;V為氣槍總容量;P為激發(fā)壓力;P0為環(huán)境壓力，一般是1個大氣壓。當V一定時，E與P成正比，因此可以通過模擬激發(fā)能量變化對波形振幅的影響來反映激發(fā)壓力的影響。

在其它激發(fā)條件不變的情況下，激發(fā)能量分別取1.0×106，1.3×106，1.5×106，1.7×106 J，根據(jù)能量震級轉換，激發(fā)能量為1.3×106 J，相當于大約0.8級地震的能量。模擬結果（圖11）顯示，信號振幅隨氣槍激發(fā)能量的增加而增加，二者呈近線性關系，且激發(fā)能量引起的振幅變化不受距離的影響。

1.2.3震源沉放深度

氣槍陣列的沉放深度決定了氣槍陣列與水庫底部和水面的距離，會對氣槍地震信號產生影響。為了研究沉放深度對有限水體中氣槍震源信號的影響，本文進行了不同沉放深度的情況模擬。激發(fā)條件一致時，固定水體水位為20 m，震源分別沉放于7～17 m處，結果顯示，振幅隨沉放深度增大而增大，且垂直向振幅大于水平向振幅（圖12）。

為了分析由震源沉放深度引起的振幅變化，選取震源沉放深度范圍為8～10 m，改變其沉放深度，得到振幅變化率隨距離的分布如圖13所示：水平向的變化幅度大于垂直向變化幅度，距離為2.0 km范圍內的信號振幅變化率呈周期性振蕩，距離大于2.0 km的信號振幅變化率則變化幅度較小。

2分析討論

數(shù)值模擬結果顯示，在近場面波傳播速度小于體波傳播速度，使模擬波形中由振幅更大的面波占主導，隨著波形傳播距離的增加，體波與面波到時差逐漸增大，P波和S波震相逐漸清晰;在相對較遠距離上的波形則會由P波和S波為主導。對于水位變化的模擬，當水位為13～40 m時，對振幅的影響呈非線性狀態(tài)的;水位為13～15 m時，振幅隨水位增加而減小，這可能與其傳播路徑有關，在水中消耗能量更多，使得振幅變小;當水位為15～34 m時，振幅隨水位變化總體呈正相關，這是由于隨著水庫水位的增加，水對水庫底的壓強增大，水庫底部面積也增大，使得水庫底部所承受壓力增大，而氣槍信號的振幅與水庫底部壓力成正比，因此水位增加會引起氣槍信號的振幅增大;在水位為34 m時，達到最大波形振幅，該段水位就是氣槍激發(fā)試驗的優(yōu)勢激發(fā)水位;當水位為20～40 m時，水面寬度不變，對應的Gaussian形狀庫體的邊界會有相應的傾角變化，對于庫體邊界傾角變化所帶來的影響，會在之后的工作中進行深入地分析。

在波形向外傳播的過程中，由水位變化引起的振幅波動緩慢減小，表明水體效應的影響隨距離逐漸減小。通過具體模擬不同幅度的水位變化，發(fā)現(xiàn)水體振蕩會產生駐波效應，這種駐波使得波形振幅受水位的變化呈周期振蕩形式，而其影響范圍約為10倍水面寬度的距離，超過這個距離后，駐波效應逐漸消失，振幅變化逐漸減小。水位變化對波形水平向影響大于垂直向，可能是因為水平向的能量主要通過P波轉換而來，而垂直向分量的能量主要通過S波轉換而來，這與由圖3得出的水平向傳播速度更快，可能其P波轉換波所占比重更大相吻合。因此，水平向受水位變化的影響更大，而垂直向相對更小。通過擬合不同水位變化幅度與其產生的平均振幅變化率，得到二者之間的冪函數(shù)關系，由此可以為實際波形運用中去除水位影響提供參考和理論依據(jù)。

水庫大容量氣槍試驗中，氣槍總容量一定時，激發(fā)壓力與激發(fā)能量呈正比，模擬激發(fā)能量變化對波形振幅的影響與陳蒙（2014）關于賓川氣槍信號特征的結論一致，激發(fā)能量與波形振幅成線性關系。當氣槍工作壓力增加時，激發(fā)產生的氣泡內的壓力增大，造成對應的氣泡半徑及氣泡壁運動速度也相對較大，使得對應的氣泡脈沖的振幅變大。

數(shù)值模擬震源沉放深度的變化對波場傳播特征的影響結果顯示：信號最大振幅與震源沉放深度總體呈線性遞增的關系，這可能是因為氣槍沉放深度越深、靜水壓越大、氣泡激發(fā)和振蕩過程中與水體的耦合越好，因此氣槍激發(fā)聲波能量越有效，使得接收的波形振幅越大。而震源沉放深度的影響效應隨距離的增加在緩慢減小。

3結論

水庫大容量氣槍激發(fā)震源信號對水位、激發(fā)能量和震源沉放深度等激發(fā)條件存在一定的依賴。通過本文數(shù)值模擬分析，得到以下結論：水庫激發(fā)氣槍震源試驗中，水庫水位對振幅的影響呈非線性狀態(tài)，15～34 m時，振幅隨水位變化總體呈正相關;34 m為氣槍激發(fā)試驗的優(yōu)勢激發(fā)水位，能產生最大波形振幅能量。水位變化引起的振幅波動隨距離的增加緩慢減小，在震中距為水面寬度10倍的范圍內受水體振蕩產生的駐波影響，振幅呈周期振蕩形式變化，超過這個距離后駐波效應逐漸減小，且水位變化對水平向振幅的影響要大于垂直向。通過擬合不同水位變化幅度與其產生的平均振幅變化率，得到二者之間存在冪函數(shù)關系。因此，可以在實際波形運用中，參考水位變化幅度產生的振幅變化率，去除或盡可能減小水位變化帶來的影響。波形振幅與激發(fā)能量及震源沉放深度呈近線性關系，即激發(fā)能量越大，震源沉放深度越深，氣槍激發(fā)效果越好，越有利于進行遠距離深穿透地下結構的探測。

本文通過數(shù)值模擬得到不同激發(fā)條件對水庫氣槍源信號的影響特征，能夠為解釋實際試驗結論提供一定的參考意義，但該模擬中仍受到計算條件及成本的限制，僅采用了二維介質模型及參考震源時間函數(shù)進行計算，尚不能達到實際氣槍激發(fā)試驗中所呈現(xiàn)的激發(fā)條件的復雜精細程度，與實際氣槍信號特征還存在一些定量的差異，因此，需要更為精細的模型介質、更精確的震源時間函數(shù)以及更優(yōu)的計算方法進行模擬，從而為實際氣槍震源信號的應用研究提供可靠的基礎。

參考文獻：

陳蒙.2014.利用水庫大容量非調制氣槍陣列進行區(qū)域尺度地下結構探測和監(jiān)測[D].北京：中國地震局地球物理研究所.

陳颙，李宜晉.2007.地震波雷達研究展望：用人工震源探測大陸地殼結構[J].中國科學技術大學學報，37（8）：813-819.

陳颙，王寶善，姚華建.2017.大陸地殼結構的氣槍震源探測及其應用[J].中國科學：地球科學，47（10）：1153-1165.

陳颙，張先康，丘學林，等.2007.陸地人工激發(fā)地震波的一種新方法[J].科學通報，52：1317-1321.

胡久鵬，王寶善，陳颙.2017.水體形狀對陸地氣槍激發(fā)信號的影響[J].地震研究，40（4）：543-549.

林建民，王寶善，葛洪魁，等.2008.大容量氣槍震源特征及地震波傳播的震相分析[J].地球物理學報，51（1）：206-212.

林建民，王寶善，葛洪魁，等.2010.大容量氣槍震源子波激發(fā)特性分析[J].地球物理學報，53（2）：342-349.

羅桂純，王寶善，葛洪魁，等.2006.氣槍震源在地球深部結構探測中的應用研究進展[J].地球物理學進展，21（2）：400-407.

孫楠，孫耀充，庾汕.2017.含有限水體介質中地震波場數(shù)值模擬[J].地震研究，40（4）：557-564.

唐杰，王寶善，葛洪魁，等.2009.大容量氣槍震源的實驗與模擬研究[J].中國地震，25（1）：1-10.

王寶善，葛洪魁，王彬，等.2016.利用人工重復震源進行地下介質結構及其變化研究的探索和進展[J].中國地震，32（2）：168-179.

王寶善，王偉濤，葛洪魁，等.2011.人工震源地下介質變化動態(tài)監(jiān)測[J].地球科學進展，26（3）：249-256.

王彬，李孝賓，劉自鳳，等.2016.賓川地震信號發(fā)射臺的震源系統(tǒng)、觀測系統(tǒng)和觀測結果[J].中國地震，32（2）：193-201.

王偉濤，王寶善，蔣生淼，等.2017.利用氣槍震源探測大陸淺部的地震學研究回顧與展望[J].地震研究，40（4）：514-523.

魏斌，蘇金波，王海濤，等.2016.新疆呼圖壁人工水體大容量氣槍信號發(fā)射臺性能研究[J].中國地震，32（2）：222-230.

徐逸鶴，王寶善，王偉濤.2016.利用固定臺站分析長江激發(fā)氣槍信號特征[J].中國地震，32（2）：282-295.

姚道平，張藝峰，閆培，等.2016.臺灣海峽大容量氣槍震源海陸聯(lián)測初探[J].地震學報，38（2）：167-178.

翟秋實，姚華建，王寶善.2016.氣槍震源資料反褶積方法及處理流程研究[J].地震研究，32（2）：295-304.

張元生，郭曉，秦滿忠，等.2016.甘肅祁連山主動源重復探測項目建設及震源重復性分析[J].中國地震，32（2）：209-215.

Cerjan C，Kosloff D，Kosloff R，et al.1985.A nonreflecting boundary condition for discrete acoustic and elastic wave equations[J].Geophysics，50（4）：705-708.

Chen M，Yang W，Wang W，et al.2014.Influencing factors of seismic signals generated by un-tuned large volume airgun array in a land reservoir[J].Earthquake Science， 27（4）：365-376.

Chen Y，Liu L B，Ge H K，et al.2008.Using an airgun array in a Land reservoir as the seismic source for seismotectonic studies in Northern China：experiments and preliminary results[J].Geophysical Prospecting， 56（4）：601-612.

Dragoset B.2000.Introduction to air guns and air-gun arrays[J].The leading Edge，19（8）：892-897.

Hixon R.1997.On Increasing the Accuracy of macCormack scheme for Aeroacoustic Applications[J].AIAA paper：29-39.

MacCormack R W.1969.The effect of viscosity in hypervelocity impact cratering[J].Journal of Spacecraft and Rockets， 40（5）：69-354.

Reasenberg P A，Aki K.1974.A precises，continuous measurement of seismic velocity for monitoring in situ stress[J].Journal of Geophysical Research， 79（B2）：399-406.

Ronen S.2002.Psi，pascal，bars，and decibels[J].The Leading Edge，21：60-61.

Sun N，Sun Y C.2019.Numerical simulation of the Binchuan airgun source affected by water body[J].Earthquake Research in China， 2019，33（2）：208-219.

Sun Y C，Zhang W，Xu J K，et al.2017.Numerical simulation of 2-D seismic wave propagation in the presence of a topographic fluid-solid Interface at the sea bottom by the curvilinear grid finite-difference method[J].Geophysical Journal International，210：1721-1738.

Sun Y，Zhang W，Chen X.2016.Seismic-wave modeling in the presence of surface topography in 2D general anisotropic media by a curvilinear grid finite difference method[J].Bulletin of the Seismological Society of America，106（3）：1036-1054.

Wang B，Yang W，Wang W，et al.2020.Diurnal and semidiurnal P-and S-wave velocity changes measured using an airgun source[J].Journal of Geophysical Research：Solid Earth，125（1）doi：10.102912019JB01828.

Zhang W，Chen X.2006.Traction image method for irregular free surface boundaries in finite difference seismic wave simulation[J].Geophysical Journal International，167（1）：337-353.

Zhang W，Zhang Z，Chen X.2012.Three-dimensional anisotropic seismic wave modeling in spherical coordinates by a collocated-grid finite-difference method[J].Geophysical Journal International， 188（3）：1359-1381.

Effect of Excitation Factors for Numerically Simulation on Airguan

Signal Amplitude in Binchuan Reservoir

SUN Nan1，2，SUN Yaochong3

（1.School of Earth and Space Sciences，University of Science and Technology of China，Hefei 230026，Anhui，China）

（2.Yunnan Earthquake Agency，Kunming 650224，Yunnan，China）

（3.Department of Earth and Space Sciences，Southern University of Science and Technology，Shenzhen 518055，Guangdong，China）

Abstract

Using the finite different method，we numerically simulate the effect of excitation factors on airgun signal in Binchuan Reservoir.The result shows that the relationship between the change of reservoir water level and airgun signal amplitude is nonlinear，there is an optimum water level range of 30～35 m for airgun firing test which can excitate the strongest energy of signal amplitude，in addition the influence of water level changing attenuates with distances.We also fit the power equation between the amplitude of water level changing and the average amplitude change rate it produced，so that we can use it to provide theoretical reference for removing the effect of water level changing in actual waveform application.The wave amplitude is linear with excitation energy and towing depth，that is the greater the energy and the deeper of the towing，the better the effect of excitation，the more conducive to detect remote and deep penetration underground structure.

Keywords：numerical simulation;water level;towing depth;excitation energy;signal amplitude