基于棧式自編碼器的土質邊坡失穩風險評估

于 錦，譚 飛，仝德富，郭永楠，馬邦闖

(中國地質大學工程學院(武漢)，湖北 武漢 430074)

邊坡失穩產生的滑坡災害同地震災害、火山災害一樣已經成為影響人類生存和發展的三大地質災害之一。我國每年由于各種滑坡造成的經濟損失高達200億元[1]。因此，開展邊坡風險管理，有效地判斷出邊坡的風險等級，指導邊坡的施工，并降低施工風險，確保生產安全具有重大的意義。

在邊坡失穩風險評估方面，國內外學者進行了大量的研究。如Li等[2]基于有限元與可靠度理論確定了邊坡最危險滑裂面和滑動體體積，據此定量分析了邊坡風險的影響因素和損失；Xiao等[3]提出了一種輔助隨機有限元法，在考慮土體性質空間變異性的情況下，可有效地對三維邊坡進行可靠性分析和風險評估；Zhang等[4]基于層次分析法和模糊識別理論建立了膨脹土邊坡失穩風險分析模型；Ferrero等[5]基于精確的地質結構調查，評估了邊坡穩定性條件；Pinheiro等[6]通過對影響邊坡的9個參數分配權重計算得到邊坡質量系數，并根據經驗劃定邊坡質量系數等級，進而評估邊坡失穩風險；Macciotta等[7]定量化計算了邊坡失效的風險，力求最小化邊坡失效風險評估過程中的不確定性因素；Mori等[8]基于地形數據，提出了一種在暴雨工況下邊坡失穩風險評估模型；李東升[9]將可靠度理論與風險評估結合，以決策樹作為分析工具，在考慮邊坡工程投資和相應風險的基礎上，進行邊坡工程風險決策，在一定程度上消除了決策過程中人為因素的影響，使決策更具科學性；張雷等[10]在分析高等級公路邊坡工程風險因子的基礎上，應用層次分析法對邊坡失穩風險等級進行了評估研究；何海鷹等[11]基于層次分析法，利用巖質邊坡風險的諸多影響因素建立了巖質高邊坡風險評估指標體系；梁濤等[12]基于模糊層次分析法原理、步驟和MATLAB語言環境，通過需求分析、界面設計、代碼編寫、功能模塊設計等流程，研發出公路邊坡風險評估軟件RASlope；李典慶等[13]基于子集模擬的邊坡風險評估的高效隨機有限元法，推導出基于子集模擬的邊坡失效概率和失效風險的計算公式。

上述研究中，大多采用模糊集理論、層次分析法、有限元理論等建立了邊坡失穩風險評估模型，或是采用概率論方法計算邊坡失效概率并確定邊坡失穩風險等級，或是考慮一些特殊工況下邊坡風險的影響因素，而在確定邊坡風險影響因素的權重值或概率時，通常采用專家打分法、頭腦風暴法、事故樹分析法、頻率統計法等方法，其中一些方法存在許多人為主觀因素的影響，且計算權重的過程也較為繁瑣。

深度學習源自于機器學習，是一門人工智能科學。機器學習發展至今，最重要的網絡模型即人工神經網絡模型。深度學習是人工神經網絡的進一步深入，也稱為深度神經網絡，它較普通BP神經網絡具有更深的結構層次、更多的激活函數種類、更多的模型結構、更加智能等特點，主要包括卷積神經網絡[14]、深度信念網絡[15]、循環神經網絡[16]、自編碼器神經網絡[17]等。其中，自編碼器神經網絡能降低數據維度，獲取最優初始參數，是一種無監督學習的神經網絡，它可以不斷地調整參數以重構經過壓縮的輸入樣本。而棧式自編碼器是自編碼器的一種多層組合，當維度壓縮到合適的狀態、參數足夠優化時，將多個自編碼器連接可得到棧式自編碼器。本文基于深度學習模型——棧式自編碼器開展了土質邊坡失穩風險評估研究，可快速評估土質邊坡失穩風險，并克服了傳統方法計算量大、處理過程復雜等缺陷，以提高邊坡風險管理效率。

1 土質邊坡穩定性影響因素的確定

影響土質邊坡穩定性的因素較多，一般基于最主要的控制性因素開展土質邊坡穩定性研究。如夏元友等[18]以土體容重、黏聚力、內摩擦角、邊坡角、邊坡高度、孔隙水壓力(孔隙水壓力系數)6個主要因素為研究對象，應用RBF神經網絡開展了土質邊坡穩定性影響因素的敏感性分析；馮夏庭等[19]同樣基于上述6個土體參數，應用BP神經網絡開展了土質邊坡穩定性評價；高超等[20]以上述6個土體參數中的5個土體參數為研究對象，應用神經網絡開展了黃草壩古滑坡穩定性研究。可見，上述6個因素是影響土質邊坡穩定性的最主要因素。此外，夏季暴雨時節往往是滑坡災害發生的高發時期，因此水的影響不可忽視；地震對土質邊坡的影響同樣巨大，強震之下土體振動液化時有發生；人類生產生活也會加劇滑坡風險。因此，本文基于上述影響土質邊坡穩定性的6個主要土體參數以及年均降雨量、抗震烈度、人類活動共9個因素，開展了土質邊坡失穩風險評估研究。

在對土質邊坡穩定性各影響因素的風險等級進行劃分時，應做到合理布局，風險等級劃分過多、過于細化，則會使數據處理過程較復雜，模型訓練耗時加大，不利于工程應用；若風險等級劃分過少、過于簡單，則針對性、差異性不強，總風險評級結果則不具參考價值。土質邊坡穩定性的風險等級劃分后采用類似二進制方式進行標定處理，方便數據在模型中的輸入和輸出，有利于提高模型的訓練效率和預測結果的準確性。本文在詳細閱讀和分析相關文獻[21-25]的基礎上，將土質邊坡失穩風險分為3級，1～3級邊坡失穩風險程度遞增(見表1)，并采用類似二進制方式對每個風險等級進行標定，標定值見表1；分別將上述9個影響因素劃分為4～5個風險等級，也采用類似二進制方式對各影響因素的每個風險等級進行標定，其標定值見表2。

表1 土質邊坡失穩風險的分級與標定

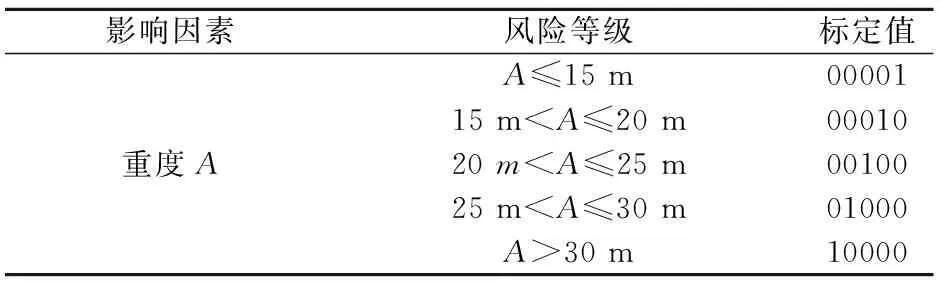
表2 土質邊坡穩定性影響因素風險的分級與標定

續表2

2 棧式自編碼器網絡結構

圖1 自編碼器(三層結構)Fig.1 Autoencoder (three-layer structure)

棧式自編碼器由自編碼器堆疊構成。自編碼器包括編碼和解碼兩個部分，數據先通過輸入層進入中間層進行編碼，然后壓縮成更低維度的數據，從中提取數據特征，最后進入重構層解碼還原數據，見圖1。經過多組數據訓練后，模型可學習到數據的特征及其映射關系。輸入數據xi的編碼過程如下式：

yj=f[(wij)Txi+bj]

(1)

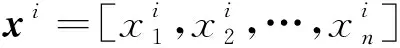
(2)

(3)

f(x)=max(0,x)

(4)

由上述3個函數式可知，Sigmoid函數的值域為[0,1]，Tanh函數的值域為[-1,1]，Relu函數的值域為[0,+∞]。而本文對各影響因素值進行標定后，每個因素都被轉換為0、1表示，因此應用Sigmoid函數作為本模型的激活函數是合適且可行的，見圖2。

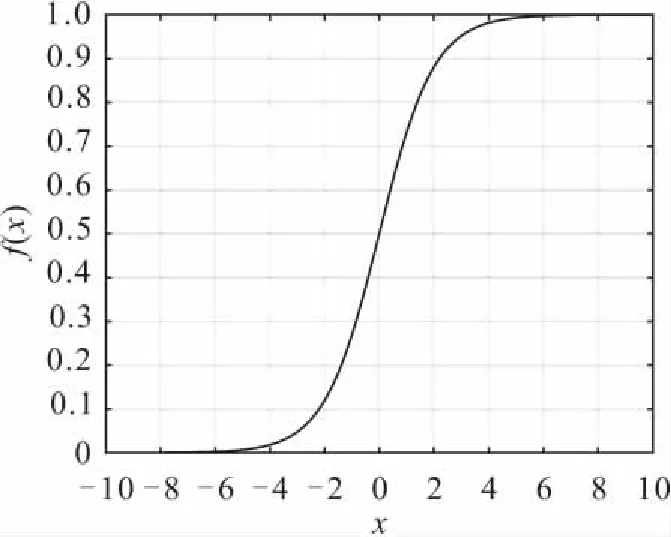
圖2 Sigmoid函數Fig.2 Sigmoid function

中間層與重構層之間的解碼過程如下式：

(5)

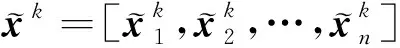
(6)

(7)

重構層誤差項計算公式為

(8)

式中:δk為重構層k上的誤差項；zk為重構層的輸入值。

中間層誤差項計算公式為

(9)

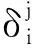
依據上面公式計算得到的誤差項需進行連接權值和偏置值的修正。

重構層權值的修正公式為

wjk(n+1)=wjk(n)+η·δk·yj

(10)

式中:η為學習效率；n為權重w被修正的次數。

中間層權值的修正公式為

wjk(n+1)=wij(n)+η·δj·xi

(11)

重構層偏置的修正公式為

bk(n+1)=bk(n)+η·δk

(12)

中間層偏置的修正公式為

bj(n+1)=bj(n)+η·δj

(13)

輸入一個樣本數據即進行一次上述運算時，則表示完成了一個樣本數據的學習。遍歷一次訓練樣本，即完成一次訓練。當重構值與輸入值之間的誤差達到要求精度，停止模型訓練，輸入測試樣本，進行泛化能力測試。

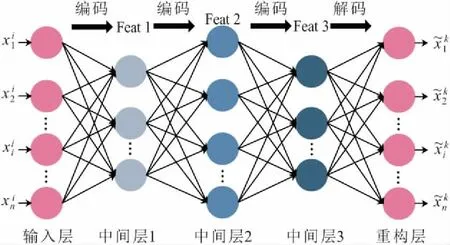
圖3 棧式自編碼器結構Fig.3 Structure of stacked autoencoder

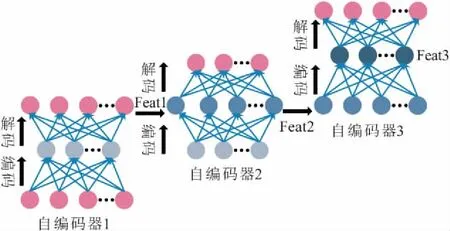
圖4 棧式自編碼器的訓練過程Fig.4 Training process of stacked autoencoder

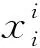
3 模型構建與訓練

本次研究從某高速公路施工便道邊坡和湖北秭歸縣、巴東縣等邊坡工程收集了44個邊坡樣本，邊坡樣本土體以粉質黏土為主，土體容重介于10～24 kN/m2，邊坡高度介于1～75 m，邊坡角介于20°～75°，黏聚力介于10～25 kPa，內摩擦角介于0°～45°，孔隙水壓力系數介于0～1。地震、降雨和人類活動頻度依據邊坡所在地的實際情況確定。為了避免模型訓練過程產生過擬合、精度不高等問題，借鑒深度學習中數據增強(Data Augmentation)的方法將樣本集數據增強到156個。數據增強的目的是讓有限的數據產生更多的等價數據，增加訓練樣本的數量和多樣性(噪聲數據)，提升模型魯棒性[26]。數據增強方法在圖像識別等深度學習模型中應用較為廣泛，主要操作方法包括幾何變換(旋轉、翻轉、裁剪、拼接等)、色彩空間變換、隨機擦除、對抗訓練、神經風格遷移等。通過生成隨機數為樣本序號，隨機劃分136個訓練樣本和20個測試樣本，并依據表1和表2對樣本數據進行標定處理。

對樣本數據標定之后，輸入數據維數由9變為39，輸出數據維數為3。初步擬定使用一個編碼器，樣本數據將由39個維度(39個神經元)降低到18個維度(18個神經元)，再經分類層(3個神經元)輸出，見圖5。自編碼器的激活函數采用Sigmoid函數，分類層采用Softmax函數，自編碼器單獨的無監督訓練采用二次代價函數，即以公式(6)為誤差函數，分類層訓練和棧式自編碼器有監督情況下的微調均采用交叉熵代價函數，即以公式(7)為誤差函數。自編碼器單獨訓練時，訓練誤差隨迭代次數的變化見圖6。

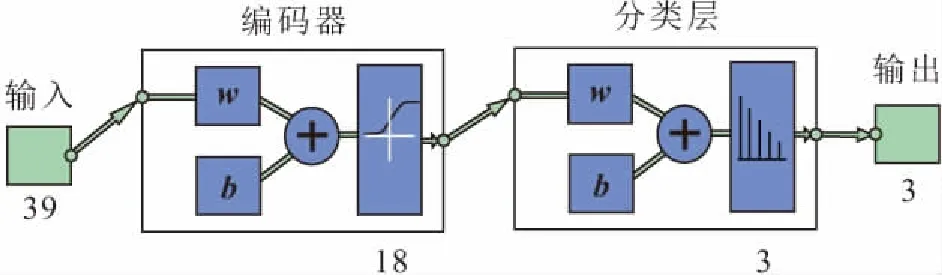
圖5 土質邊坡失穩風險評估棧式自編碼器Fig.5 Stacked autoencoder of instability risk assessment of soil slope

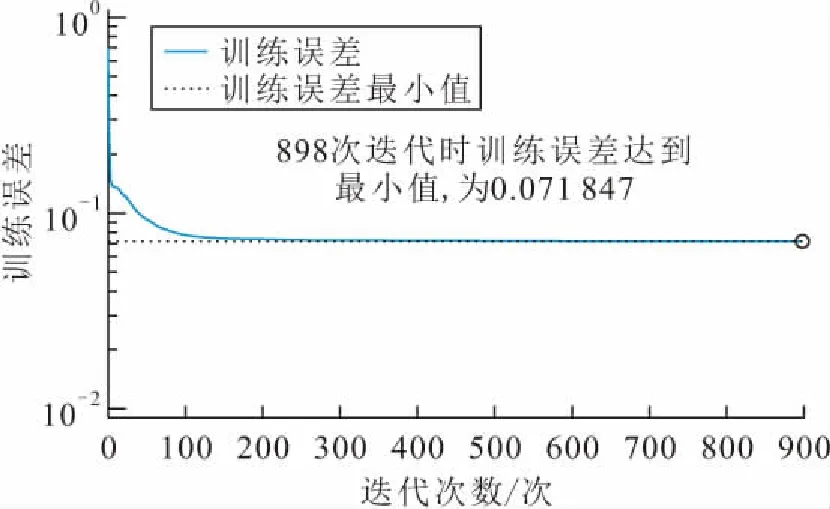
圖6 自編碼器訓練誤差隨迭代次數的變化Fig.6 Variation of training error of autoencoder with the number of iterations

由圖6可見，當自編碼器訓練到898次時，訓練誤差最小值約為0.07，可判定此時的精度基本達到要求，可結束訓練。

4 模型泛化能力測試

經過訓練后，對模型泛化能力進行測試，得到20個測試樣本的預測輸出值與目標值的對比以及模型泛化能力測試精度的混淆矩陣，見表3和圖7。

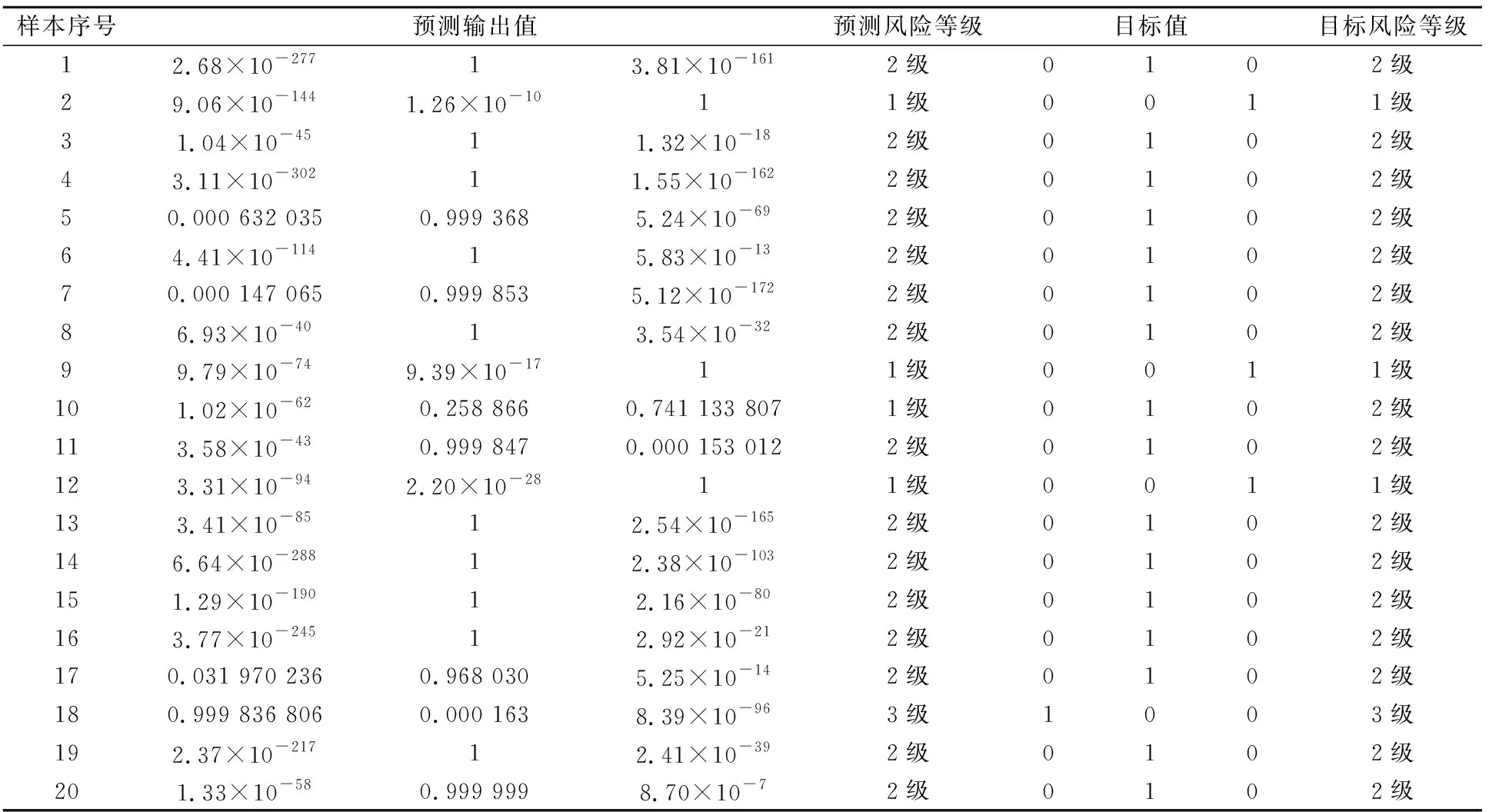
表3 模型泛化能力測試結果

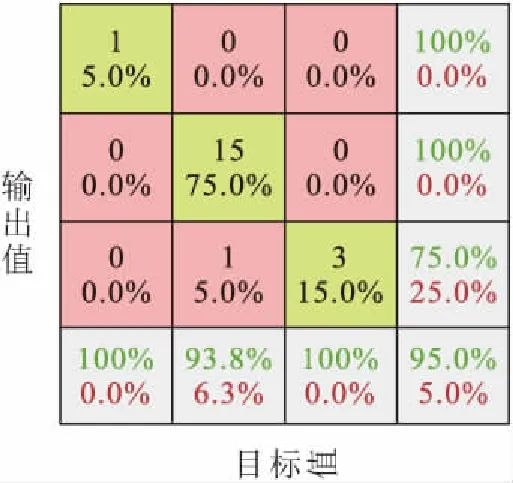
圖7 模型泛化能力測試精度的混淆矩陣Fig.7 Confusion matrix of accuracy of generalization ability test accuracy of the model

由表3和圖7可見，本文提出的土質邊坡失穩風險評估模型，獲得了數值上95%的準確率；除10號樣本未達到預期值外，其他樣本均得到了高精度的預測輸出值。由此可見，本文應用棧式自編碼器建立的土質邊坡失穩風險評估模型是可行且有效的，可將該模型應用于土質邊坡工程失穩的風險等級評估。

5 結論與建議

本文基于棧式自編碼器深度學習模型，提出了一種快速評估土質邊坡失穩風險的方法，主要得到以下結論：

(1) 運用棧式自編碼器建立的土質邊坡失穩風險評估模型具有計算速度快、評估結果客觀性高等特點，并獲得了數值上95%的準確率，說明應用深度學習模型構建風險評估模型進行土質邊坡失穩風險評估是可行且有效的。

(2) 本文提出的方法僅需依據工程勘察資料，獲取邊坡穩定性的9個影響因素后，即可快速預測得到邊坡失穩的風險等級。由于邊坡狀態會隨著氣候、人類活動等外界因素而發生變化，運用本方法可在邊坡的不同階段和不同狀態下，多次快速地確定邊坡失穩的風險等級，從而為開展邊坡全壽命風險管理節約了成本，加快了邊坡失穩風險等級評估過程。

(3) 深度學習中有許多模型可以利用，將性能更佳的深度學習模型運用于邊坡、隧道、地下空間工程的風險評估、變形預測、超前地質預報等研究，將可獲得更多意義重大的研究成果，這也是今后的研究方向。