基于矩陣運算的極小碰集求解方法

陳旭琳，趙相福，褚 鵬，陳中育

(浙江師范大學 數學與計算機科學學院，浙江 金華 321004)

0 引 言

隨著科技的發展，各行各業的系統越來越復雜精密，傳統的專家系統診斷方法已越來越難以高效應對[1]。為了適應系統規模不斷擴大的現狀，避免分析耗時過長等問題[2]，排除專家診斷的主觀干擾因素，人們提出基于模型的診斷[3]。通常，基于模型的診斷分為沖突識別[4]和候選產生[5]兩步：第一步沖突識別是對比預期行為和觀測結果得到極小沖突集[6]，而后的第二步候選產生是根據已知的沖突集簇求出系統的極小碰集[7]。由Reiter所著故障診斷領域的經典論文可知，這些極小碰集是可能導致系統故障的原因，即系統的候選診斷[8]。顯然，為了提高求解候選診斷的效率，必須提高求解全體極小碰集的效率[9]。本文研究在已知沖突集簇時求解極小碰集的算法。

求解極小碰集被證明是NP-hard問題[10]，眾多研究人員對極小碰集算法進行全面的研究和深入的改進[11]，目前已經存在許多算法，包括HS-Tree算法、HST-Tree算法、CSSE-Tree算法、蛛網算法、CHS-Tree算法等。這些算法存在各自的優缺點和特定的適用范圍，主要缺點集中體現在幾個方面：需要建立樹或圖，缺乏明顯的規律，數據結構及算法的實現較繁瑣；需要進行剪枝，而剪枝過程可能會丟失正確解；用基于樹結構的算法，一般均需要首先建立樹，再由樹經過較復雜的遞歸計算才能產生碰集。

本文針對上述求解極小碰集算法的缺點，提出一種基于矩陣運算求解極小碰集的方法，這種算法直接通過矩陣乘法運算求解，即將碰集求解的問題轉化為矩陣的乘法運算問題。算法的主要優點是：該算法不需要建立樹或圖，數據結構非常簡單，易于程序實現；該算法不需要進行剪枝，因而不會因剪枝而丟失正確解；該算法思路和流程相對簡潔清晰；矩陣的性質保證結果的正確性；不需要將沖突集簡化為極小沖突集，直接使用沖突集求解；某些情況下算法的求解效率較高。

1 預備知識

以下系統性介紹一些基于模型診斷的相關概念和基礎定理。

定義1 一個系統定義為一個三元組 (SD,COMPS,OBS)， 其中：

(1)SD是系統描述，是一階謂詞公式的集合，包含診斷中的主要信息；

(2)COMPS是系統中組成部件的集合，一般用有限常量集 {c1,c2,…,cn} 表示；

(3)OBS是系統觀測值的集合，是用一階謂詞公式表示的有限集合。

在待診斷的設備中，使用一元謂詞AB(·)表示“abnormal”(反常)，即系統實際的行為與系統預期的行為不相同。另外，如果系統部件發生故障，但實際輸出與預期輸出相一致，則仍認為不是“反常”。AB(c)為真時，當且僅當c反常，其中c∈COMPS。

定義2 沖突集(CS)也稱為沖突部件集，是一個部件集 {c1,c2,…,cn}?COMPS， 使得SD∪OBS∪{～AB(c1),～AB(c2),…,～AB(cn)} 不一致。當沖突集的任意真子集都不是沖突集時，該沖突集被稱為極小沖突集(MCS)。

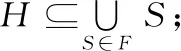
定義4 若集合S1和S2滿足S2?S1， 則稱S1為S2的真超集。

下面通過例1對上述概念進行說明。

例1：假設一個系統的沖突集簇F={{1,2},{1,3},{1,2,3},{1,4},{2,4}}， 包含系統部件1、2、3、4，{1}、{2}、{1,4}、{1,3,4}、{2,3,4}是該集合簇的部分候選解，其中，{1,4}、{1,3,4}和{2,3,4}是碰集，并且只有{1,4}、{2,3,4}是極小碰集。由于集合{1,3,4}為集合{1,4}的真超集，因而集合{1,3,4}不是極小碰集。

2 矩陣計算極小碰集

2.1 算法描述

下面對使用矩陣求解極小碰集的算法進行簡述，算法步驟如下：

步驟1 將沖突集簇以某種轉換規則轉換為矩陣A。

集合與矩陣轉換規則1規定如下：定義m×n參數矩陣，其中m為沖突集合簇中包含沖突集的個數，n為沖突集合簇中包含系統部件的個數。矩陣中第i行第j列的值aij表示第i個沖突集是否包含第j個系統部件，若是則值為1，否則為0。

步驟2 統計沖突集簇中系統部件的個數，根據系統部件的個數枚舉出系統部件的所有可能的組合，即所有候選解。一般而言，將所有候選解按照部件編號從小到大，部件個數從少到多有序排列。將所有候選解按照指定規則轉換為矩陣B。

集合與矩陣轉換規則2規定如下：定義n×v參數矩陣，其中n為沖突集合簇中包含系統部件的個數，v為候選解的個數。矩陣中第x行第y列的值bxy表示第y個候選解中是否包含第x個系統部件，若是則值為1，否則為0。

步驟3 將矩陣A與矩陣B相乘得到m×v的參數矩陣C，即C=A×B。 矩陣C中第y列全為非0時，矩陣B中第y列對應的候選解為碰集。

步驟4 得到所有碰集后，刪除其中的真超集，即可得到極小碰集。

2.2 算法驗證

(1)充分性

aikbky=1時，當且僅當aik=1，bky=1， 即第i個沖突集中有第k個系統部件，第y個候選解中也有第k個系統部件。所以，第i個沖突集和第y個候選解有交集。

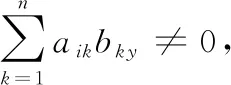
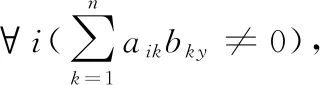
由碰集的定義可知，第y個候選解一定是一個碰集。充分性得證。

(2)必要性

設第y個候選解是一個碰集。

按照算法2.1，一定會有候選解符合要求，即碰集可以由算法2.1得到。必要性得證。

(3)正確性

算法的正確性體現在兩個方面。

一方面，輸入與輸出之間的關系是正確的。輸入數據是沖突集簇，沖突集簇轉化為矩陣A，并根據其中部件個數生成矩陣B，其對應所有候選解。通過矩陣乘法運算，可以求出矩陣B中符合碰集條件的列，也就是從候選解中找出碰集，去超集之后就能輸出所有極小碰集。

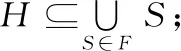
2.3 復雜度分析

假設該算法的總運行時間為T，主要與矩陣乘法運算的時間相關。在矩陣相乘得到矩陣C的過程中，求得矩陣C的每一個數值需要循環n次，時間復雜度為O(n)。每列包含m個數值，為了得到整列數值需要循環m次，時間復雜度為O(nm)。矩陣C有2n-1列，為了得到整個矩陣的數值需要循環2n-1次，時間復雜度為O(mn2n)。由于T≈O(mn2n)， 所以該算法的時間復雜度約為O(2n)。由于需要存儲所有候選解，空間復雜度取決于候選解的個數。枚舉得到候選解的個數為2n-1，算法的空間復雜度也為O(2n)。

3 實例執行

根據上述提出的基于矩陣求解極小碰集的算法和過程，舉例分析如下：

例2：仍然考慮例1中的沖突集簇F={{1,2},{1,3},{1,2,3},{1,4},{2,4}}， 使用矩陣方法求解所有極小碰集具體步驟如下：

步驟1 沖突集簇包含5個沖突集，4個系統部件，構造5×4參數矩陣。第1個沖突集{1,2}包含第1個、第2個系統部件，所以矩陣中第1行的第1列和第2列(即a11和a12)為1；不包含第3個、第4個系統部件，所以第3列和第4列(即a13和a14)為0。同理，根據其它沖突集可以得到矩陣中其它數據，最終得到矩陣A如下

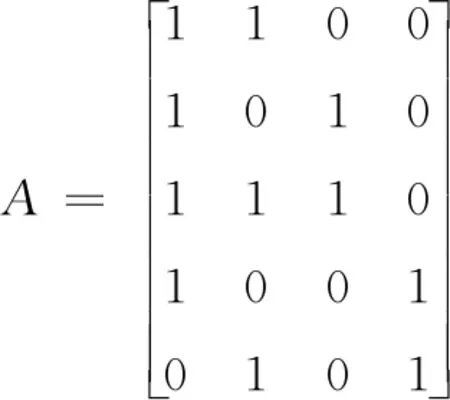
步驟2 沖突集簇中系統部件的數量為4，由4個部件可以枚舉出15種組合，構造4×15參數矩陣。候選解有{1}、{2}、{1,2}、{3}、{1,3}、{2,3}、{1,2,3}、…、{1,2,3,4}。第1個候選解{1}包含第1個系統部件，不包含第2個、第3個、第4個系統部件，所以矩陣中第1列的第1行(即b11)為1，其它(即b21、b31和b41)全為0。同理，根據其它候選解可以得到矩陣中其它數據，最終得到矩陣B如下

步驟3 將上述兩個矩陣相乘，得到一個5×15的新矩陣C

矩陣C中第3、7、9、11、13、14、15列的值全為非0，所以矩陣B中第3、7、9、11、13、14、15列對應的候選解為碰集

步驟4 矩陣B中第3列的第1行、第2行為1，第3行、第4行為0，所以第3個候選解包含第1個、第2個系統部件，不包含第3個、第4個系統部件，對應的集合為{1,2}。同理，矩陣B中第7、9、11、13、14、15列對應的集合為{1,2,3}、{1,4}、{1,2,4}、{1,3,4}、{2,3,4}、{1,2,3,4}，即碰集有{1,2}、{1,2,3}、{1,4}、{1,2,4}、{1,3,4}、{2,3,4}、{1,2,3,4}，去真超集得到極小碰集{1,2}、{1,4}、{2,3,4}。所以，{1,2}、{1,4}、{2,3,4}就是沖突集簇F的極小碰集，也就是系統的最小診斷解。

4 比較分析

為了分析算法求解效率，本節將基于矩陣求解極小碰集的算法與主流的樹形結構算法進行比較，包括CSSE-Tree算法、HST-Tree算法。這里設置沖突集簇數據如下： {1,1+k}， {2,2+k}， {3,3+k}，…，{k,2k}。 其中，k表示沖突集簇中包含的集合個數。每一組數據測試10次，將平均值作為最后結果。運行環境為Windows10操作系統(Intel(R) Core(TM) i5-3427U CPU@1.80 GHz 2.30 GHz，4 GB內存)，使用Microsoft Visual C++6.0編程，運行結果見表1和圖1。

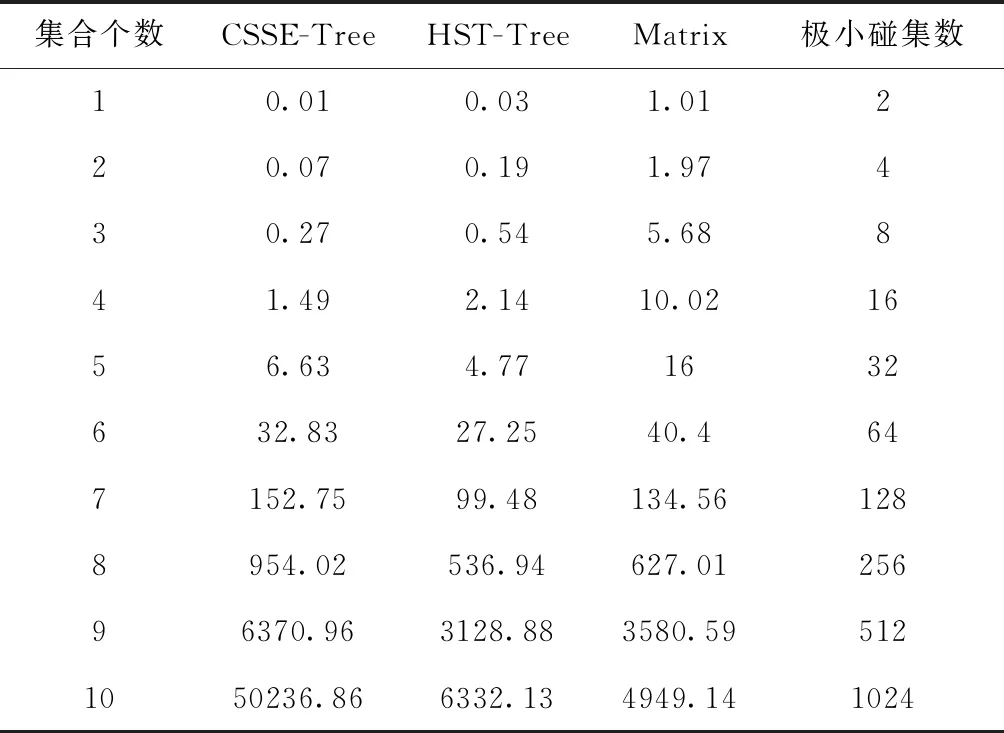
表1 CSSE-Tree、HST-Tree和矩陣算法運行時間對比/ms

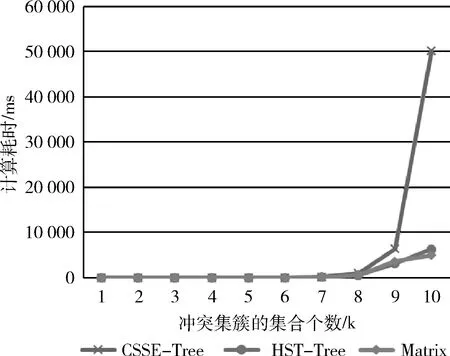
圖1 CSSE-Tree、HST-Tree和矩陣算法運行時間對比

比較表1和圖1中的數據，可以得出結論：①相對于這幾種樹形結構算法，本文提出的基于矩陣運算求解極小碰集的方法運行效率較好，具有一定優勢；②當沖突集簇的集合個數k較小時，基于矩陣運算的方法沒有優勢，幾種算法的運行時間相近。當集合個數k增加時，基于矩陣運算的方法時間長勢最為平緩，運行時間不會隨著沖突集簇中集合個數的增加而急速增長，因此，該算法更具有適用性；③基于矩陣運算的方法能求出所有極小碰集，不會丟失正確解。

通過分析算法運行結果，可以得出如下結論：①基于矩陣運算的極小碰集求解方法不需要生成結點和建立樹形結構，數據結構簡單，只需要數組就可以編程實現；②該算法計算過程較為簡單，不需要遞歸調用，只需要進行簡單的數學計算，運算速度較快；③該算法考慮所有可能解，并且不需要進行剪枝，因此不會丟失任何極小碰集；④當沖突集簇中的集合個數較多時，基于矩陣運算的方法具有比較明顯的優勢；⑤使用該算法求解極小碰集時，求解效率與沖突集的排列順序無關，對于一個沖突集簇，無論沖突集排列順序如何變化，算法運行時間不受影響。

綜上所述，相較于CSSE-Tree、HST-Tree等算法，基于矩陣求解極小碰集的算法具有較好的效率，更適合應用于實際的故障診斷問題中。在給定特殊沖突集簇，比如沖突集簇的集合個數較多時，基于矩陣求解的運行效率明顯高于其它算法。

5 結束語

自極小碰集問題提出至今，國內外大量專家學者投身于該問題的研究中，并且獲得了豐碩的成果。本文提出一種全新的算法，基于矩陣運算求解極小碰集。該算法將集合簇以一種轉換規則轉換為矩陣，通過數學計算在矩陣中體現碰集的特性，從而求出所有極小碰集。與傳統方法相比，該算法易于理解且編程簡單，無需構造樹，實現環境要求低，在大部分開發平臺上都可實現，具有較高的求解效率，在某些情況下具有突出優勢。通過矩陣運算排除碰集中的真超集，直接得到所有極小碰集，是未來進一步研究工作。