逃逸均值簡化粒子群優化算法

陸松建，司偉立，韓 娟,3,4，李質彬

(1.重慶郵電大學 通信與信息工程學院，重慶 400065；2.中國科學院計算技術研究所 移動計算與新型終端北京市重點實驗室，北京 100190；3.中國科學院計算技術研究所 無線通信技術研究中心，北京 100190；4.中國科學院大學 計算機與控制學院，北京 100049)

0 引 言

粒子群優化(particle swarm optimization，PSO)算法存在易陷入局部極值、過早收斂和收斂精度低等問題[1-4]。為解決PSO算法存在的問題，目前提出的改進方法大致分為4類：基于粒子初始化的改進，如文獻[5]中利用Hammersley對粒子位置進行初始化，使初始種群能夠均勻覆蓋整個搜索空間；基于粒子群速度更新公式的改進，包括參數調節和公式自身改進二種方式，如動態調整慣性權重粒子群算法[6]、二階振蕩策略粒子群算法[7]，該類方法通過均衡算法全局與局部尋優能力，加強算法跳出局部最優的能力；基于分群策略的改進，如文獻[8]將整個種群分為PSO機制迭代分群和混沌機制迭代分群，有利于增強種群多樣性避免陷入局部極值中；基于混合機制的改進，利用其它算法優勢幫助粒子群算法跳出局部最優，如模擬退火粒子群算法[9]、混沌粒子群算法[10]、免疫粒子群算法[11]等，混合算法尋優性能較好，但混合機制使得算法變得更加的復雜與繁瑣。

本文基于前人的研究，提出了一種逃逸均值簡化粒子群優化(escape mean simplified particle swarm optimization，EMSPSO)算法，EMSPSO算法不使用速度更新公式，在簡化粒子群優化算法的基礎上，加入均值搜索策略和逃逸策略，保證極快收斂速度的同時有效地改善PSO算法易陷入局部最優的問題。仿真實驗中，引入5個標準測試函數，將本文算法與其它改進算法進行對比實驗，驗證EMSPSO算法的有效性。

1 標準粒子群優化算法

(1)

(2)

其中，x=1,2,…,n；d=1,2,…,D；t=1,2,…,M；r1和r2為區間[0,1]上均勻分布的隨機數；M為種群最大進化代數；c1和c2為學習因子，分別代表個體的“自我認知”能力和群體的“社會引導”功能，c1,c2∈[0,2]；w為慣性權重，可以均衡種群的全局和局部尋優能力，w∈[0,1]； 為了預防粒子跳出解空間的搜索區間，一般設置vid∈[-vmax,vmax]，vmax為用戶自行設置的常數，代表粒子的最大飛行速度；進化停止條件為預設的最大進化代數或(和)預設的目標精度閥值。

2 逃逸均值簡化粒子群優化算法

2.1 簡化粒子群優化算法

標準PSO算法包含速度和位置更新項，大多數改進PSO算法對速度、位置更新項增加某些操作算子，例如混沌[10]、自適應調節參數[12]、變異[13]等操作提高算法的收斂速度和精度，使得PSO算法的描述越來越復雜，同時，也使得定量分析算法的收斂性變得更加的復雜。

文獻[12]嘗試舍棄PSO算法中速度更新項，使算法達到最簡化，仿真實驗結果表明這種改進對算法穩定性影響不大，同時提高了算法的搜索效率。本文同樣舍棄標準PSO算法中速度更新項，僅由位置更新項的指導進行全局尋優，得到簡化粒子群優化算法(simplified particle swarm optimization，SPSO)，其公式如下

(3)

SPSO算法沒有粒子速度更新概念，避免了人為設置 [-vmax,vmax] 而影響粒子的收斂速度和精度，同時，使得算法更加的簡化便于對算法的進化過程進行分析。

2.2 均值搜索策略

SPSO算法無速度更新項，僅由個體粒子最優解和全體粒子最優解引導粒子進行位置更新，進化過程中，無速度因子的牽制，避免了粒子在收斂后期由于速度更新出現“發散”現象，導致粒子收斂速度慢、收斂精度低的問題。解決單峰值問題時，SPSO算法的收斂速度快、收斂精度高，但對于復雜的多峰值多局部解問題，由于無速度因子的牽制，粒子位置趨向于全局最優解更新幅度過大，導致粒子種群多樣性差，全局尋優能力低，易陷于局部最優解。

(4)

式中：第一項舍棄SPSO算法中慣性權重因子w， 利用均值策略替代其它改進SPSO算法中通過調節w的方式均衡算法全局與局部尋優能力，簡化了算法的操作；第二項和第三項為粒子個體最優位置和全體最優位置的線性組合。

MSPSO算法和SPSO算法進化過程如圖1所示。

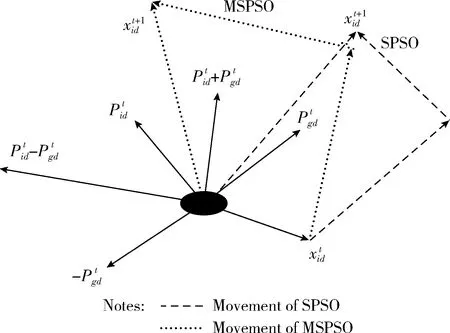
圖1 MSPSO算法和SPSO算法進化過程對比

(5)

到了進化后期t→∞時，根據式(5)關系式，式(4)可變為

(6)

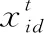
2.3 逃逸策略

粒子進化過程中，無論是早熟收斂還是全局收斂，群體中的粒子都會出現嚴重“聚集”現象，此時種群多樣性匱乏[13]，如果粒子早熟收斂陷入局部最優解，因周圍已經過高密度搜索，難以突破局部最優解。因此，當出現早熟收斂時，需提供一種機制，跳出當前局部最優解。

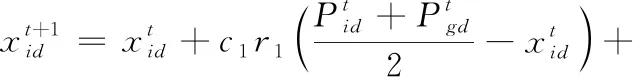
(7)

式中：r3為區間[0,1]上均勻分布的隨機數；kt為逃逸控制因子，當不滿足逃逸條件下，其值為0，否則代表逃逸的半徑，即

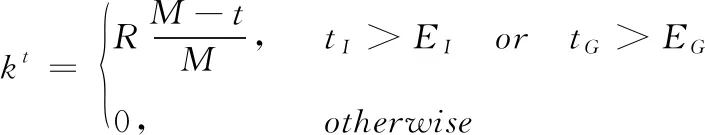
(8)

式中：t為當前進化代數；M為最大總進化代數；R為半徑控制因子，控制粒子逃逸的半徑，本文算法R取值為1；tI,tG分別為個體最優解停滯代數和全體最優解停滯代數；EI,EG為個體最優解最大停滯代數閥值和全體最優解最大停滯代數閥值，一般取值范圍為3～8。

分析式(8)可知，當不滿足逃逸條件時，公式退化為式(4)；當滿足逃逸條件時，在進化前期，kt為較大值，粒子逃逸半徑較大，加強全局尋優能力；在進化后期，kt為較小值，加強后期收斂能力。

2.4 算法步驟

EMSPSO算法實現步驟如下：

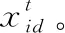
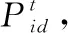
步驟3 進入進化過程，根據式(8)計算逃逸控制因子kt。

步驟4 根據式(7)更新各粒子位置，并計算各粒子位置更新后的適度值，更新個體最優解和全體最優解。

步驟5 判斷個體最優解或全體最優解是否處于停滯狀態，如果處于停滯狀態，則分別累加各自的停滯代數tI或tG。 否則，直接執行步驟6。

步驟6 如果當前進化代數小于預設的最大進化代數或(和)當前全體最優解適度值未達到預設的目標精度閥值，則重復執行步驟3～步驟6。否則，執行步驟7。

步驟7 輸出種群搜索到的最優解，進化停止，算法尋優結束。

3 仿真實驗及對比分析

3.1 測試函數

為全面體現改進算法的有效性，本文從所有常用標準測試函數中挑選出5個具代表性的測試函數進行仿真對比。其中包括以Sphere為代表的單峰值函數、以Rastrigin為代表的這一類復雜多峰多局部解函數、提供極少優化信息難以極小化的Rosenbrock病態單峰二次函數、含噪聲影響的Quartic函數及最優值為負數的Inverted Consine Wave函數。函數具體表達式見表1，其中D代表函數的維數。

3.2 實驗設計及參數設置

本文使用Matlab R2014a進行仿真實驗，仿真環境為Windows 7系統運行下在Intel(R) Core(TM) i5-75003.4 GHz的處理器中進行。在相同仿真環境與參數設置條件下，將本文改進的算法與PSO算法、改進二階振蕩粒子群優化算法(improved second-order oscillatory particle swarm optimization，ISOPSO)[7]、自適應簡化粒子群優化算法(self-adjusted simplified particle swarm optimization，SASPSO)[12]進行對比實驗，從收斂速度、收斂精度和穩定度3個方面驗證EMSPSO算法的性能。

表1 5種標準測試函數

對比算法中各參數設置均如下：種群數量n=40； 最大總進化代數M=100； 學習因子c1=c2=2； 最小慣性權重wmin=0.4， 最大慣性權重wmax=0.9， 固定慣性權重w=0.8； 個體最優解最大停滯代數閥值EI=3， 全體最優解最大停滯代數閥值EG=5； 半徑控制因子R=1。 為保證測試結果不具隨機性，每個算法獨立運行50次，對測試結果取平均作為更可靠的依據。

性能評估采用如下方法：

(1)總進化代數設置為100，固定進化代數情況下評估各算法解決10維問題、50維問題時收斂速度和精度。

(2)總進化代數設置為1000，固定各測試函數的目標收斂精度，評估各算法解決50維問題時達到目標收斂精度所需的平均進化代數和50次搜索中能達到目標收斂精度的搜索成功率。

3.3 收斂速度和收斂精度對比

為體現不同算法的優劣性，固定各算法總進化代數為100，從最優值、平均值、標準差、平均運行時間(s)等統計特性對算法進行評估。每個算法獨立運行50次，最優值指50次搜索中搜索結果的最優值；平均值指50次搜索中搜索結果的平均值；標準差指各算法搜索結果偏離均值的程度，用于判斷算法的穩定性；平均運行時間指平均運行一次算法所需要的時間。解決10維和50維的低高維度問題時，各算法搜索結果見表2。

觀察50次搜索中的最優值和平均值，EMSPSO算法對函數F1的搜索結果均優于其它對比算法；SASPSO、EMSPSO 算法均搜索到函數F2和F4的理論最優解；對于極難極小化的病態函數F3，EMSPSO算法的搜索結果更加接近于函數F3的理論最優解，而其它算法均完全偏離理論最優解；EMSPSO算法對函數F5的搜索結果略差于SASPSO算法，其差距較小，收斂精度已達到很好的效果。

觀察標準差，EMSPSO算法除對函數F3和F5的搜索結果略差于SASPSO算法外，對其它函數搜索結果均優于其它對比算法。而對于病態函數F3，雖然SASPSO算法標準差最小，但搜索到的最優值已完全偏離F3函數的理論最優解，因此，該算法對函數F3標準差性能的評估已失去意義。

觀察平均運行時間，SASPSO算法平均運行時間最長，其算法通過添加鎖定因子和自適應調節慣性權重的方式取得較好的尋優性能，但同時加大了算法運行時間，而 EMSPSO 算法取得更好性能的同時平均運行時間低于SASPSO算法，EMSPSO算法的平均運行時間更接近于其它3個算法，時間復雜度更低。

通過以上分析可知，改進算法無論解決低、高維度問題，都能保持良好的搜索性能，除對函數F5的搜索性能略差于SASPSO算法外，改進算法對其它函數的搜索，其收斂精度更高、結果波動性更小；對于含有較少尋優信息的病態函數F3，EMSPSO算法通過逃逸操作跳出局部最優解，使種群在解空間的其它區域繼續搜索從而搜索到了全局最優解，搜索到的最優解更加接近于函數F3的理論最優解，而其它算法已經完全偏離理論最優解。綜上分析可知，EMSPSO算法的整體尋優性能優于其它對比算法。

鑒于篇幅原因，以下選取其中3個50維函數的搜索進化曲線進一步觀察算法性能，其中橫坐標為進化代數，縱坐標為50次搜索結果平均適度值的對數。

各算法對Sphere函數的搜索進化曲線如圖2所示，當到達最大進化代數時，EMSPSO算法更加接近于理論0值解，收斂精度最高。

表2 各算法解決10維和50維問題時搜索結果對比

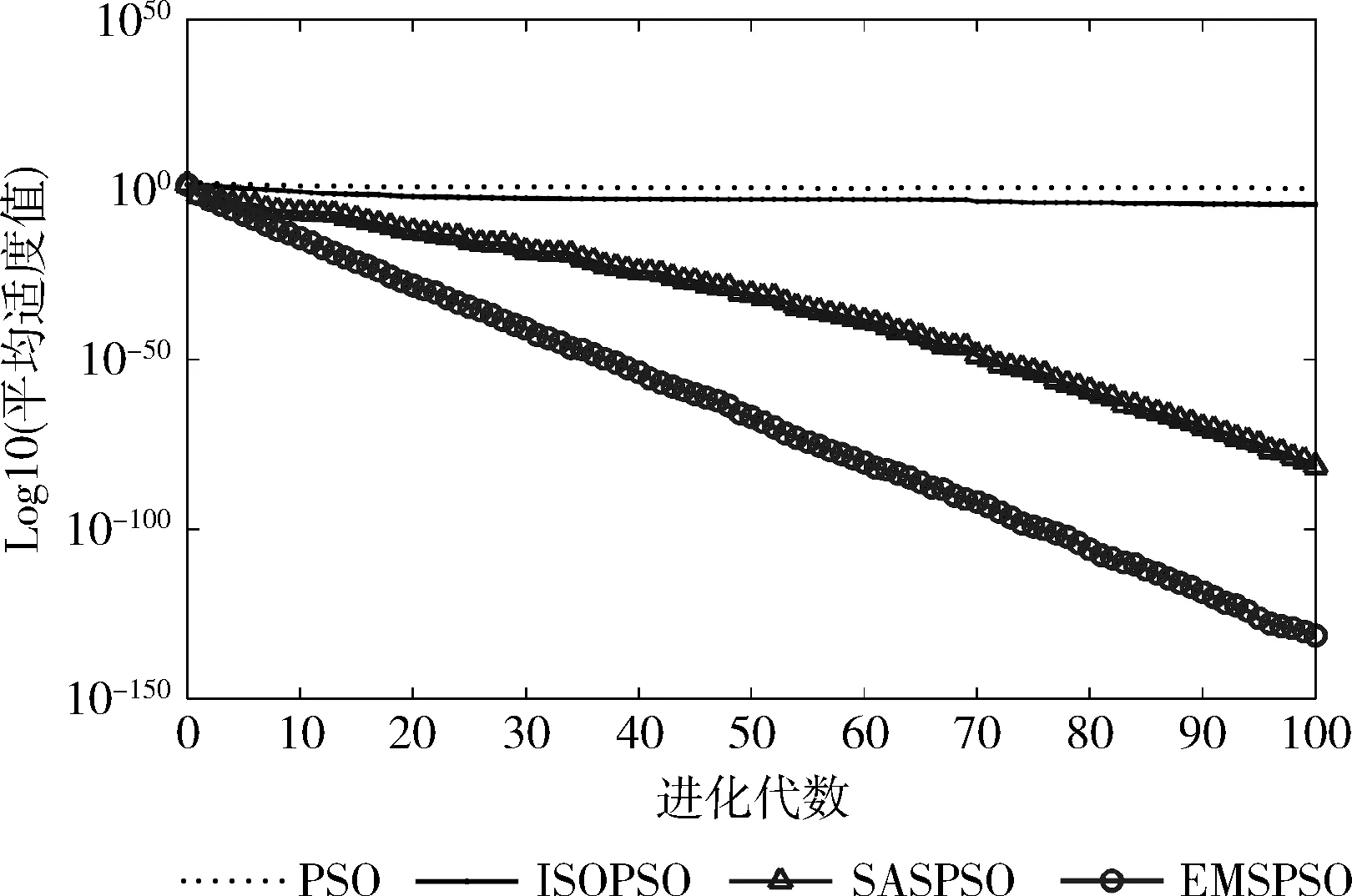
圖2 50維Sphere函數搜索進化曲線對比

各算法對Rastrigin函數的搜索進化曲線如圖3所示，在第12代進化左右EMSPSO算法的搜索結果已達到該函數的理論最優解，到達理論最優解所需的進化代數最少，收斂速度最快。

圖3 50維Rastrigin函數搜索進化曲線對比

各算法對Rosenbrock函數的搜索進化曲線如圖4所示，EMSPSO算法對Rosenbrock函數的搜索一直在逐漸逼近函數理論最優解，而其它對比算法在第15代進化左右就已陷入某個局部解中，處于搜索停滯狀態。

圖4 50維Rosenbrock函數搜索進化曲線對比

從圖2～圖4可看出，EMSPSO算法對各函數的搜索均能在20次進化代數內達到較好的收斂精度，算法收斂速度快，且進化曲線位于其它算法的下方，收斂精度更高。

3.4 平均進化代數和搜索成功率對比

表3為總進化代數為1000、重復運行50次條件下，各算法解決50維問題時達到函數目標精度所需的平均進化次數和搜索成功率對比。其中，目標精度代表解決50維函數問題所期望達到的收斂精度；平均進化次數=達到函數目標收斂精度所需進化代數總和÷達到函數目標收斂精度運行次數；搜索成功率=達到函數目標收斂精度運行次數÷總運行次數；“-”表示超過最大進化代數仍未達到函數目標收斂精度。

從表3可看出，PSO算法搜索性能最差，只有對函數F4的搜索結果能達到目標精度值，且搜索成功率較低只有34%，平均進化次數高達513.59；ISOPSO算法搜索性能相對于PSO算法更好，除函數F1外對于其它函數的搜索結果都能達到目標精度值，但搜索成功率較低；SASPSO、EMSPSO算法搜索結果均能達到函數目標收斂精度，搜索成功率高達90%以上，算法穩定性高，其中EMSPSO算法除函數F5外，達到函數目標精度所需的平均進化次數最少，搜索速度更快，性能更優。

基于以上分析結果可知，PSO算法易陷于局部最優解、收斂速度慢、收斂精度不高，其它改進算法均改善了PSO算法存在的不足，其中EMSPSO算法性能最優，主要原因在于：EMSPSO算法利用均值策略加大算法搜索范圍使得算法在進化前期搜索到全局最優解的可能性更大，并且無速度因子的牽制，使得算法收斂速度更快。如果算法陷入局部最優解中，可通過逃逸策略在其它解空間繼續搜索，增大算法搜索到全局最優解的幾率。

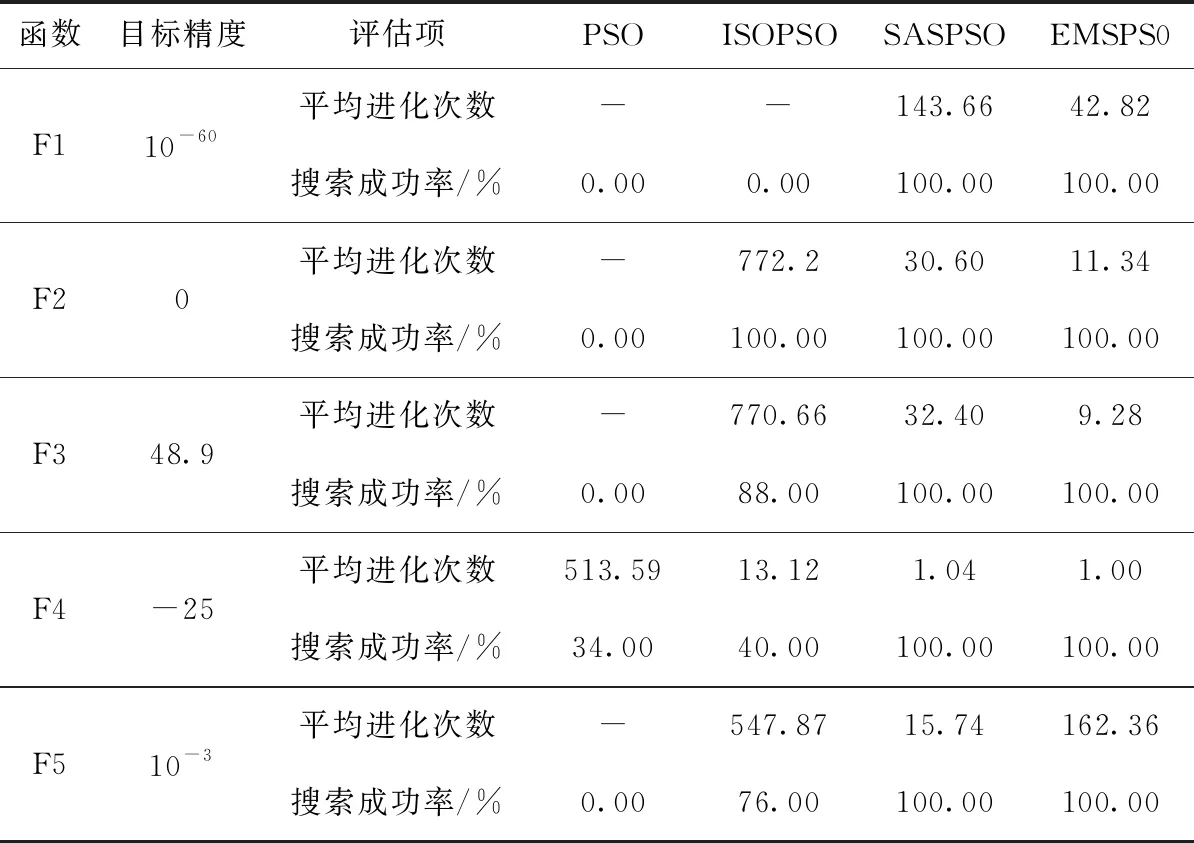
表3 解決50維問題時各算法在相同目標精度下性能評估

4 結束語

本文提出了一種逃逸均值簡化粒子群優化算法，該算法在簡化粒子群優化算法的基礎上加入均值搜索策略和逃逸策略。均值搜索策略通過個體最優解和全體最優解的線性組合引導粒子位置更新，可擴大搜索的區域范圍，提高算法的全局勘探能力。逃逸策略使進化停滯的粒子嘗試從其它解空間中繼續搜尋全局最優解，增大粒子種群多樣性，有助于跳出局部最優解，使算法更有可能搜尋到全局最優解。最后，將改進算法應用于5個標準測試函數中，并與其它改進粒子群優化算法進行仿真對照實驗，結果表明，本文改進算法全局搜索能力更強、穩定性更高，在相同目標收斂精度下所需進化次數更少，收斂速度更快。