帶擋邊關節軸承靜力學有限元分析*
戴雨靜 汪久根 陳芳華 張 斌
(1.浙江大學機械工程學院 浙江杭州 310027; 2.浙江省機電產品質量檢測所 浙江杭州 310051)
關節軸承是一種球面滑動軸承,具有尺寸緊湊、承載能力大、抗沖擊、抗腐蝕、耐磨損、自調心、潤滑好等特點,被廣泛應用于航空航天、軍工機械、工程機械等領域[1-3]。關節軸承在工作中能夠同時承受一定的徑向力和軸向力。當載荷過大時,軸承會發生塑性變形。對關節軸承進行靜力學分析,進而預先判斷出軸承的受力特點,有助于軸承設計的改進和預防其過早失效。
隨著計算機技術的發展,國內外很多研究者都開始采用有限元分析的方法對軸承進行力學性能的分析。向定漢等[4]利用ANSYS有限元軟件對向心關節軸承進行結構優化,并對優化前后的關節軸承進行了摩擦磨損對比試驗,發現優化后的軸承耐磨性較好。劉六井和高偉[5]利用ANSYS計算了推力關節軸承分別承受軸向、徑向以及復合載荷時的壓力分布情況。曾慶良等[6]利用ANSYS有限元分析軟件對桿端關節軸承的主要承載部件進行了優化設計。KIM等[7-8]對復合材料關節軸承的磨損性能進行試驗研究,并用有限元仿真的方法對其力學性能進行了分析。GERMANEAU等[9-10]運用試驗和數值模擬相結合的方法對航空關節軸承的三維力學特性進行了分析。趙憲忠等[11]結合向心關節軸承破壞加載試驗,利用ABAQUS分析了軸承在徑向或軸向單一載荷下的力學性能。王虎奇等[12]對裝載機鉸接向心關節軸承的結構特點與承載特點進行分析,并利用有限元軟件計算出各工況下關節軸承的應力分布云圖。王哲等人[13]對向心關節軸承撐桿上節點進行了軸向加載試驗研究,并進行有限元分析,綜合分析了節點處的力學性能。吳連平和楊曉翔[14]基于ABAQUS進行了關節軸承工藝參數優化設計的虛擬正交試驗,并用實驗證明了優化結果的準確性。FANG等[15]推導出關節軸承靜態接觸應力分布的計算方法,并將計算結果與有限元分析結果相結合,研究了接觸區的邊緣效應。AGUIRREBEITIA等[16]提出了一個用來估算自潤滑向心關節軸承在復合載荷下的等效載荷的模型,由此計算出的結果與有限元分析結果相吻合。可以看出,大部分學者在對關節軸承進行有限元建模時,對軸承結構進行了簡化,忽略了油槽、油孔、擋邊等特征,這將會導致計算結果與實際情況出現一些偏差。
本文作者的研究對象為KF11028型外圈帶擋邊的向心關節軸承,為了更貼近實際情況,在建模時保留了大多數結構特征,并利用ANSYS Workbench分析了關節軸承在正常工況和偏斜工況下的應力分布,同時研究了不同大小的載荷下軸承的等效應力和接觸應力峰值。
1 有限元分析
1.1 有限元模型建立
KF11028型關節軸承的結構簡圖如圖1所示。利用Solidworks建立該種型號關節軸承的三維幾何模型,為了更加接近實際情況,模型中保留了擋邊、油槽、油孔、密封圈等特征,并且加入了軸承座零件。
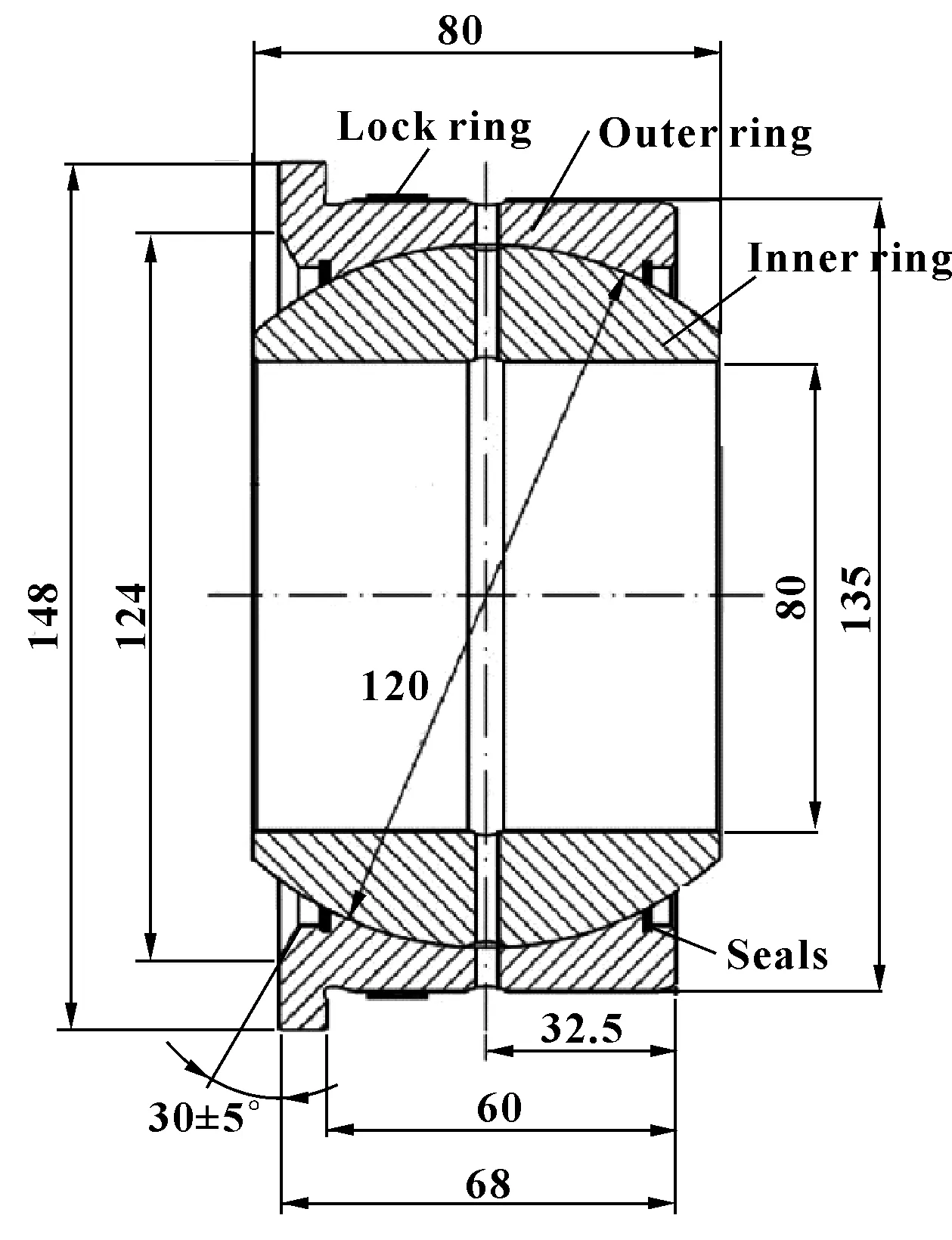
圖1 關節軸承結構簡圖(mm)
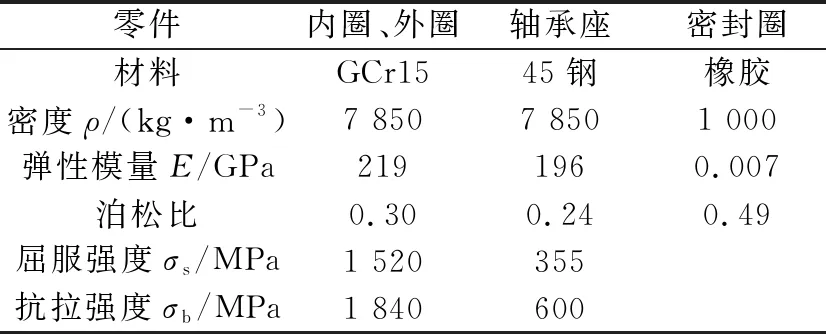
表1 關節軸承材料參數
將建立的三維模型導入ANSYS Workbench中, 按照表1數據對各零件的材料參數進行設置。并對其進行網格劃分:軸承座和密封圈采用六面體主導網格劃分,單元尺寸設置為4 mm,內外圈采用四面體網格,單元尺寸設置為3 mm。并且,由于油槽油孔處幾何形狀變化劇烈,容易出現應力集中現象,應力變化較大,因此對該處的網格進行了一定程度的細化。建立的有限元模型如圖2所示。

圖2 有限元模型
接觸設置方面:軸承座內表面與外圈外表面、外圈與密封圈之間設置為綁定接觸,接觸算法為MPC。內圈外表面與外圈內表面以及密封圈之間設置為摩擦接觸,摩擦因數取0.12,接觸算法為增強拉格朗日算法。
1.2 載荷及邊界條件設置
由于關節軸承是一種球面滑動軸承,工作過程中內圈相對外圈經常會發生偏斜。故文中分析內圈在正常和偏斜2種工況下的受力情況。載荷與邊界條件的設置如圖3所示。
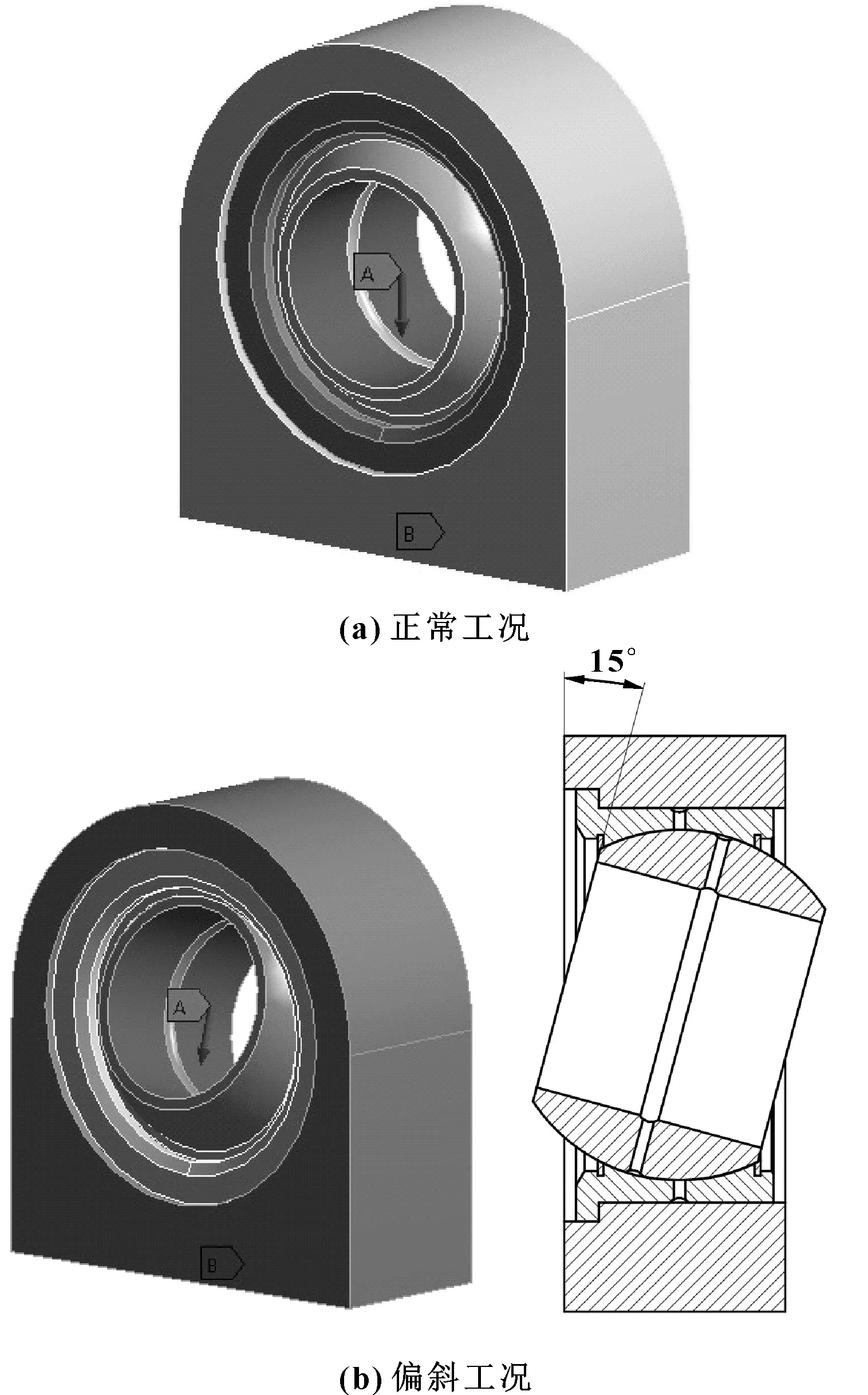
圖3 載荷及邊界條件
(1)正常工況:內圈無偏斜,內圈上施加垂直于內圓柱面的徑向載荷,軸承座底面全約束。
(2)偏斜工況:內圈偏斜15°,內圈上施加垂直于內圓柱面的徑向載荷,軸承座底面全約束。
2 計算結果及分析
圖4所示為正常工況下軸承承受1 575 kN徑向載荷時,軸承內外圈等效應力、接觸應力云圖。
由圖4可以看出,內圈內圓柱面的等效應力較大,因為該處為徑向軸承力的承載面;油槽和油孔處容易產生應力集中現象,因此這些地方的應力值也較大。等效應力的最大值出現在油孔的邊緣處,大小為1 480 MPa。外圈的等效應力最大值出現在內球面的邊緣處,大小為1 322.8 MPa。接觸應力的最大值出現在接觸面的邊緣處,大小為385.04 MPa。

圖4 正常工況下軸承靜力學分析結果
圖5所示為偏斜工況下軸承承受1 575 kN時的應力分布情況。

圖5 偏斜工況下軸承靜力學分析結果
從圖5可以看出:偏斜工況下,內圈等效應力的最大值出現在油孔的邊緣,大小為3 114.6 MPa。由于內圈的偏斜,外圈的主要受力區域往擋邊一端偏移,等效應力最大值出現在內球面位于擋邊一側的邊緣處,大小為2 296.7 MPa。接觸區域因為內圈的偏斜也發生了改變,接觸應力最大值出現在油槽邊緣,大小為731.18 MPa。
與正常工況下相比,偏斜工況下的內外圈等效應力和接觸應力的最大值更大,且內外圈的等效應力最大值均大于內外圈材料的屈服強度(1 520 MPa)。
圖6所示為內外圈的塑性變形區域,圖中A、B區域的等效應力大于材料屈服強度;可以看出,內外圈均有少量材料的等效應力大于屈服強度。內圈的塑性變形區域主要集中在油孔的兩端口,外圈的塑性變形區域主要集中在內球面位于擋邊一側的邊緣處。產生這樣結果的主要原因是軸承在這些部位的形狀急劇變化,容易產生應力集中。因此可以認為內圈的偏斜會導致關節軸承受力不均勻,從而造成部分材料發生應力集中現象,產生塑性變形,長期工作時可能會在該處形成疲勞裂紋,從而影響軸承使用性能甚至造成失效,故軸承不宜長期工作在載荷和偏斜角度都比較大的工況下。
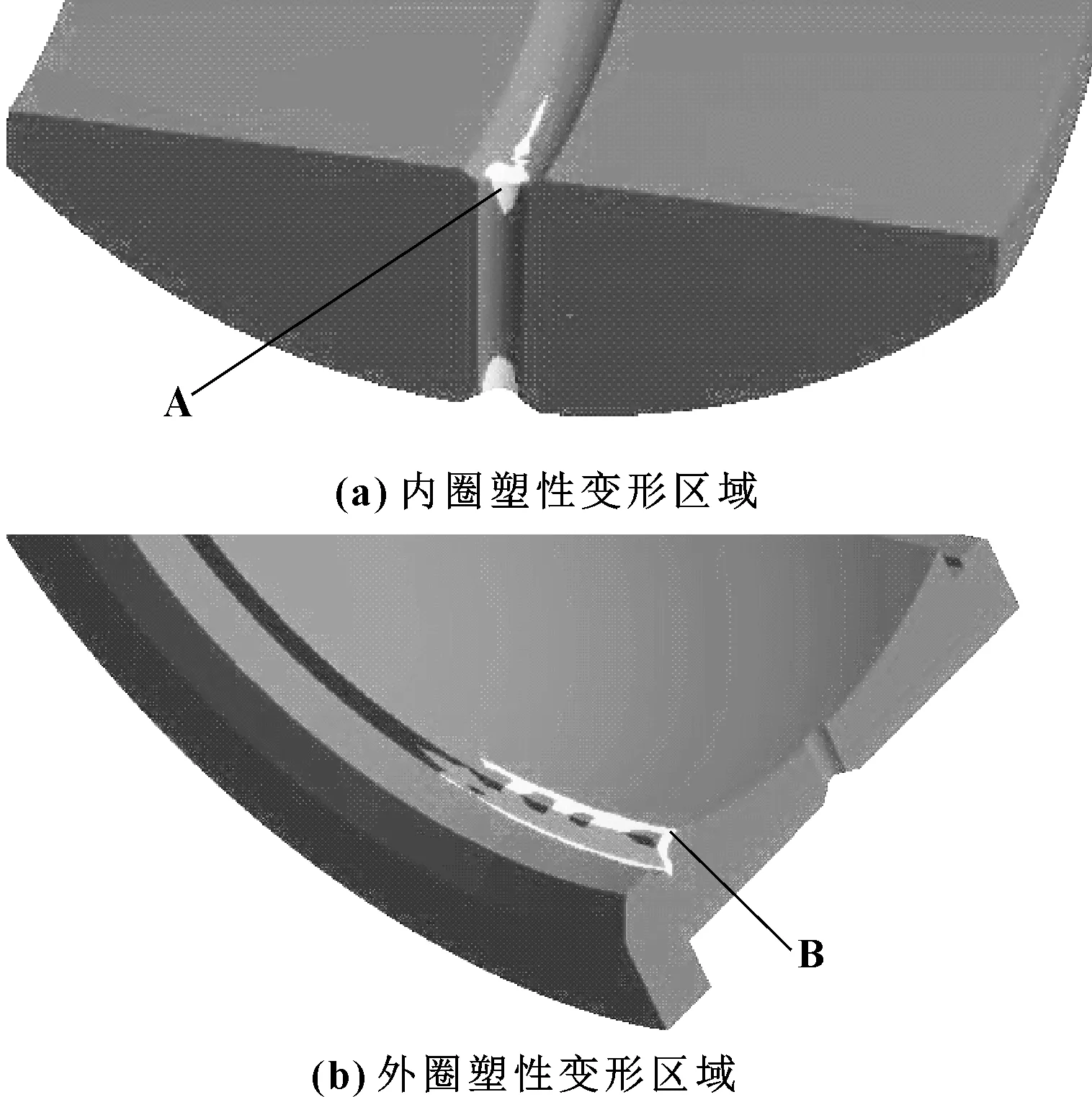
圖6 內外圈塑性變形區域
通過以上分析結果可以看出,內外圈的最大等效應力均出現在軸承幾何特征變化明顯的位置,即容易發生應力集中的位置。因此,相比于對軸承進行簡化處理的文獻,建模時考慮擋邊、油孔、油槽等結構是很有意義的,因為這些結構會影響應力分布,甚至發生應力集中。
3 結論
(1)KF11028型軸承在徑向載荷為1 575 kN的正常工況下,內圈等效應力的最大值出現在油孔的邊緣處,外圈的等效應力最大值出現在內球面的邊緣處,均小于屈服強度;接觸應力的最大值出現在接觸面的邊緣處。
(2)在徑向載荷為1 575 kN的偏斜工況下,內圈等效應力的最大值出現在油孔的邊緣處,外圈的等效應力最大值出現在內球面位于擋邊一側的邊緣處,均大于屈服強度;接觸應力的最大值出現在接觸面的邊緣處。內圈的偏斜會導致關節軸承受力不均勻,從而造成部分材料產生應力集中。故軸承不宜長期工作在載荷和偏斜角度都比較大的工況下。
(3)研究表明,內外圈的最大等效應力均出現在軸承幾何特征變化明顯的位置,即容易發生應力集中的位置。因此,建模時考慮擋邊、油孔、油槽等結構是很有意義的,因為這些結構會影響應力分布,甚至發生應力集中。

