懸浮于潤滑油中的顆粒運動分析及其對油膜壓力的影響*

韓海燕 李娜娜 尚雪梅

(西安交通大學城市學院 陜西西安 710018)

在機器運行過程中，由于實際工況及磨損等方面的影響，使得潤滑油中含有固體顆粒，而這些固體顆粒有部分會懸浮于潤滑油中。因此，研究懸浮于潤滑油中的固體顆粒的運動，同時分析顆粒運動及形狀對于油膜壓力的影響是十分必要的。進入潤滑系統的固體顆粒的形狀并不是理想化的球形，而顆粒受力分析采用的Stokes理論主要是針對球形或圓柱形顆粒，對于其他形狀的顆粒，其受力只能通過近似來求得。顆粒所受作用力的大小與諸多因素有關，例如顆粒的尺寸及形狀，這些因素的改變會導致顆粒所受作用力發生改變，利用傳統的理論方法分析這類顆粒的受力問題將面臨很大困難。因此，尋找一種簡便、穩定、可靠的方法對不同顆粒在流體運動中的受力進行模擬計算就顯得尤為重要。格子Boltzmann方法(Lattice-Boltzmann method，LBM)是近些年發展起來的一種典型的，能夠用于模擬復雜流動現象的介觀數值方法[1-3]，在兩相流及多相流[4-6]的應用中較多，近幾年也開始應用于潤滑問題的分析中[7-9]。

本文作者采用格子Boltzmann方法分析顆粒在潤滑油中的運動，同時引入顆粒輪廓參數，計入顆粒的輪廓形狀的影響，進一步修正了文獻[10]中含有固體顆粒的潤滑方程。

1 考慮顆粒形狀的潤滑問題分析

1.1 潤滑油中固體顆粒運動的LBM模擬

潤滑油中固體顆粒的受力分析采用文獻[11]中的方法，流固邊界條件的確定采用文獻[9,12]給出的方法。在LBM 模擬中，要得到懸浮于潤滑油中的固體顆粒所受的作用力，首先要得到單個固體邊界點所受作用力，其公式為

fi′(x,t+1)+fi′(x+ei,t+)-fi(x,t+)]ei

(1)

利用文獻[13-14]的邊界條件，則邊界點上的作用力為

2[fi(x,t+)-fi′(x+ei,t+)-2Bi(ei·ub)]ei

(2)

邊界點處所受到的力矩為

(3)

這樣固體顆粒在流體中受到的總的作用力及力矩分別為

(4)

(5)

式中:n為固體顆粒邊界上總的邊界點的個數，總的作用力及力矩求和在所有邊界點上進行。

在已知顆粒所受作用力和力矩的情況下，顆粒的運動速度可以由牛頓第二定律得到，顆粒運動方程如下：

(6)

(7)

式中：m為顆粒的質量；I為顆粒的轉動慣量。

顆粒的位置更新可以在每一時步對速度進行積分得到。

1.2 計入顆粒形狀的潤滑方程推導

文中考慮了顆粒輪廓形狀的影響，并在方程中引入了顆粒形狀參數，采用的潤滑模型與文獻[10]相同，由一個有限寬的楔形滑塊和一個無限長平板組成，平板及楔形滑塊分別以u1和u2的速度運動。將潤滑區域分為3個區域，將含有固體顆粒的區域II分為上下兩個部分。

若固體顆粒形心處的平動速度矢量為up，固體顆粒繞形心旋轉的角速度為ωp，則固體顆粒邊界的速度矢量ub為

ub=up+ωp×(xb-xp)

(8)

式中：xp為顆粒形心處的位置矢量；xb為顆粒邊界的位置矢量。

在文獻[14]分析中發現油膜的y向速度很小，從而導致顆粒的y向受力較小，因此，文中研究時認為顆粒只繞y軸旋轉。根據式(8)中固體顆粒邊界處的速度矢量表達式，可以得到顆粒邊界處的各個速度分量：

x向速度分量為ub=up-ωp(zb-zp)

y向速度分量為vb=vp

z向速度分量為wb=ω(xb-xp)

在顆粒邊界處采用無滑移邊界條件，即位于顆粒邊界處的潤滑油的速度與顆粒的速度相等。因此，含有固體顆粒的潤滑區域II的各速度邊界條件如下：

在區域II下部(Part A)：

(9)

在區域II上部(Part B):

(10)

式中:h1=hc-δp;h2=hc+δp;δp為顆粒的形狀參數。

若顆粒為長方體時δp=C；

若顆粒為橢圓柱體時，

(11)

式中：a和b分別為橢圓截面的長軸和短軸，當a=b時，顆粒為圓柱體。顆粒的形狀取決于顆粒形狀參數δ。

利用速度邊界條件(9)和(10)，對簡化后的N-S方程在油膜厚度方向積分，即可得到區域II的油膜速度分量，再由得到的速度對如下的連續方程進行積分：

(12)

最終得到區域II的潤滑方程為

(13)

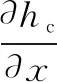
(14)

1.3 求解過程

在求解顆粒在潤滑油的運動過程時，對顆粒的運動及潤滑方程同時進行，具體的求解步驟如下：

(1)給定顆粒的初始位置及初始速度，根據該初始值進行潤滑方程的求解，得到油膜壓力及速度；

(2)根據求得的油膜壓力及速度，得到含有顆粒區域的邊界條件，采用該邊界條件對區域II進行求解，即可得到顆粒新的速度及位置；

(3)由新的顆粒速度和位置重新返回到步驟(1)進行計算，直到顆粒跳出潤滑區域此循環結束。

圖1 含有顆粒的潤滑區域更新

由于潤滑油在y方向的流動速度相對于x方向很小，因此y向潤滑油流動對于固體顆粒運動的影響也相對較小，為了縮短計算時間簡化計算，在分析顆粒運動時，采用二維分析。

2 顆粒形狀對潤滑油中固體顆粒運動的影響

將含有固體顆粒的流體區域劃分為100×30個格子，對于圓形顆粒其直徑取為9個格子，對于矩形顆粒長軸a=11，短軸b=9。在計算中對于圓形顆粒及矩形顆粒進行了分析，結果如圖2、3所示。圖中的坐標值都為格子Boltzmann方法模擬時的取值，顆粒中心在油膜厚度方向的初始位置取為lz=20。

圖2示出了圓形顆粒在潤滑油中的x向速度及z向速度的變化，可以看出，顆粒的z向速度Wp與x向速度Up相比較小；在計算中給定顆粒的初始速度為0，進入潤滑油后由于黏性流體的拖曳作用，從而速度逐漸增大，達到一定時步后，由于所受作用力的影響速度逐漸趨于平穩，即顆粒在進入潤滑油區域后，會在較短的瞬時與潤滑油速度達到一致。

圖3示出了矩形顆粒進入潤滑油后速度的變化，可以看到，隨著時步的變化顆粒的速度逐步趨于平穩，這主要是由顆粒的受力決定的；另外與圓形顆粒相比，矩形顆粒的速度趨于平穩需要更多的時間。

圖2 圓形顆粒在lz =20處速度的變化

圖3 矩形顆粒在lz=20處速度的變化

當顆粒在油膜厚度方向的初始位置lz=8時，采用相同的網格劃分分別對圓形顆粒及矩形顆粒的運動進行了計算。圓形顆粒的速度變化如圖4 所示，通過與圖2中的結果進行比較可以發現：無論顆粒位于兩壁面之間的中線(lz=15)的上側還是下側，顆粒都會向中線位置運動，在不考慮顆粒的重力時，這一結果與文獻[15]的結論一致。

圖5示出了矩形顆粒在油膜厚度方向的初始位置為lz=8時，在潤滑油中速度在初始時段的變化。可以看出，矩形顆粒在z向的運動規律與圓形顆粒相似;另一方面，還可以發現，矩形顆粒趨于平穩的速度較前面的顆粒初始位置lz=20的情況更快，這是由于當矩形顆粒位于lz=8處時，由于下壁面運動，導致離下壁面較近的區域油膜速度較大，顆粒所受流體作用力增大。

分析上述研究結果可以得到，當顆粒進入潤滑油后，經過很短的瞬時顆粒就會達到一個瞬態穩定的狀態。從前面的速度圖中可以看到，顆粒既有水平速度也有垂直速度，顆粒運動到新的位置時，其周圍的流場發生變化，使得顆粒又必然會重新調整，達到新時刻的瞬態平衡。

圖4 圓形顆粒在lz =8處的速度變化

圖5 矩形顆粒在lz =8處的速度變化

3 顆粒形狀對潤滑性能的影響

3.1 顆粒運動對于潤滑性能的影響

為分析橢圓形顆粒運動對于潤滑的影響，以顆粒速度Up=0、Up=0.5和Up=Uf為例，探討了油膜壓力的變化情況，結果如圖 6所示。由前文的分析可知，當顆粒進入潤滑油之后，其旋轉角速度很小，并且在計算中所用的時間步長也很小(數量級為10-8s)，導致顆粒在一定時段內旋轉的角度也很微小，所以文中分析忽略了旋轉角度的影響。固體顆粒在潤滑區域的位置為Xp=0.2,Yp=0.5，此時在顆粒中心處的油膜速度Uf=1.136，從圖6中可以看到，顆粒速度為0時對油膜壓力的影響較大；隨著顆粒速度逐漸增大，顆粒對油膜壓力的影響逐漸減小；而當顆粒速度等于油膜速度時，顆粒對于油膜壓力的影響很小。顆粒的存在必然會對潤滑油的流動產生一定的阻礙作用，當顆粒速度小于流體速度并與流體流動方向一致時，根據流體力學理論，顆粒與油膜之間的相對速度越小，則顆粒對于潤滑油流動產生的阻礙越小。根據上面的油膜速度值(Uf=1.136)可以發現，當顆粒速度為0時顆粒與油膜之間的相對速度最大。也可以說，圖6中的幾種情況下，顆粒速度為0時阻礙潤滑油流動的能力最強，因此顆粒速度為0時對油膜壓力的影響更大。上述研究表明，固體顆粒相對速度在顆粒運動對油膜壓力的影響中占有重要地位，因此，對于顆粒在潤滑油中運動速度的研究是很有必要的，這樣能更真實地反映固體顆粒對油膜壓力的影響。

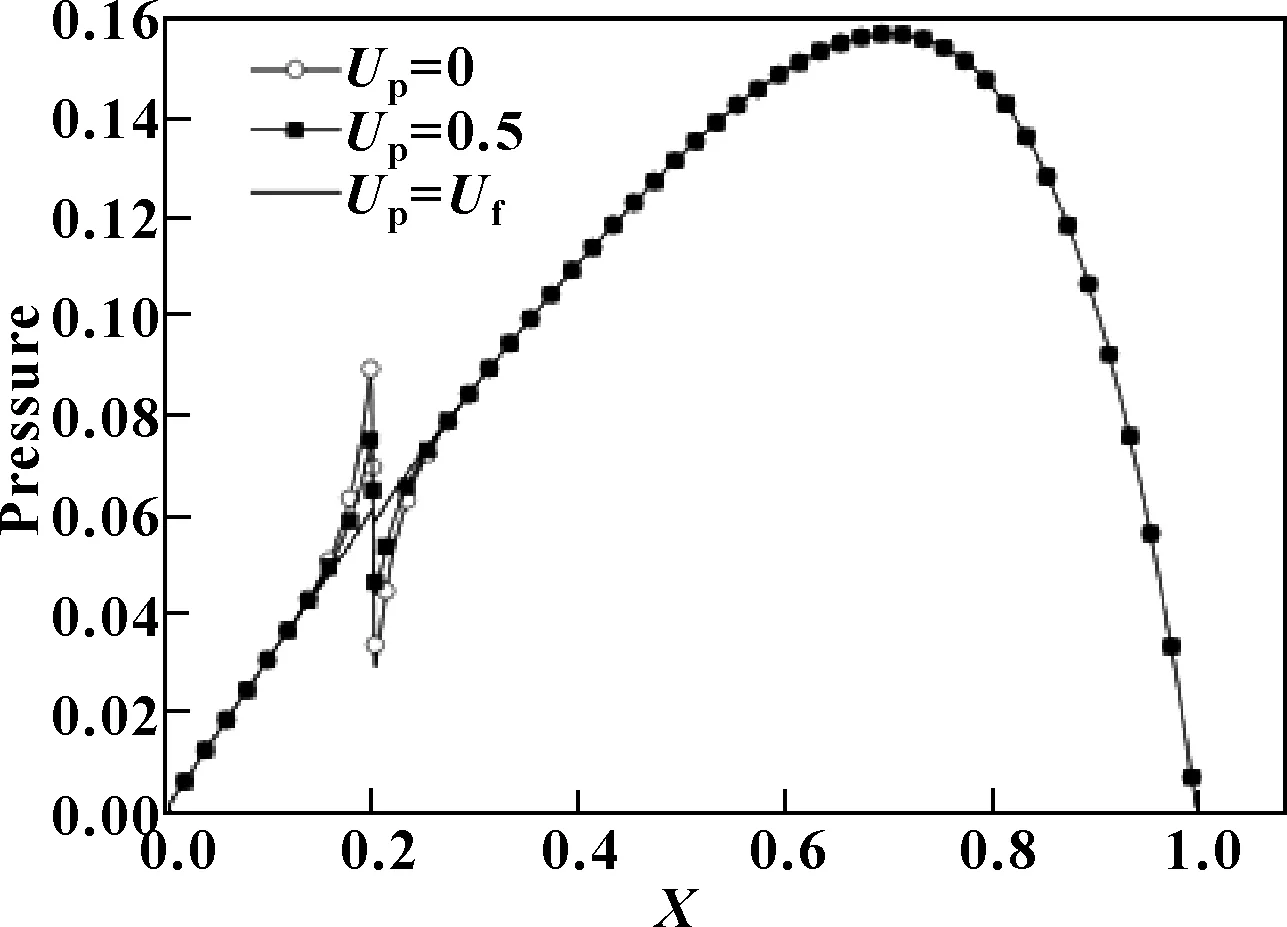
圖6 不同顆粒速度下的油膜壓力

3.2 顆粒形狀對于油膜壓力的影響

文中在討論顆粒形狀參數對于潤滑性能的影響時，主要以xoz截面形狀為圓形、橢圓形、矩形及菱形為代表進行了研究。在前面的分析中將δ計為顆粒的形狀參數，對于以上幾種不同形狀的顆粒，將x向的顆粒長度計為長軸a，z向的顆粒寬度計為短軸b，則δ的表達式分別為

圖7示出了顆粒為圓形和橢圓形時的油膜壓力隨x的變化曲線。文中分析時將顆粒在油膜厚度方向上的長度計為顆粒的寬度，用短軸b表示，而將顆粒在流動方向上的長度計為顆粒的長度，用長軸a表示。圖 7(a)中顆粒的短軸b相等，并且顆粒的位置及速度等參數都相同，可以看出，橢圓形顆粒對于油膜壓力的影響更大。這是由于對于相同尺寸的顆粒短軸，橢圓形顆粒相對應的長軸a更大，這樣就增大了區域II，從而使得顆粒對油膜壓力的影響增大。因此，可以認為，當顆粒在油膜厚度方向上的寬度一致時，長寬比越大的顆粒對于油膜壓力的影響越大。在圖 7(b)中，顆粒的長軸相同，可以看出，圓形顆粒對油膜壓力的影響更大，由于圓形顆粒在油膜厚度方向的長度尺寸較大，從而對油膜壓力的影響較大。在實際潤滑油中含有的固體顆粒不可能是規則的形狀，從上面的分析可以發現：固體顆粒尺寸在油膜厚度方向的長度一致的情況下，細長形顆粒對油膜壓力的影響較大。

圖7 圓形顆粒及橢圓形顆粒對于油膜壓力的影響

4 結論

(1)基于格子Boltzmann方法分析了顆粒在潤滑油中的受力及運動，研究發現，在不考慮顆粒重力作用時，無論顆粒在油膜厚度方向的初始位置位于兩壁面之間的中線上側還是下側，顆粒都會向中線位置移動。

(2)計入顆粒輪廓形狀的影響，修正了考慮顆粒運動的雷諾方程，分析了不同形狀顆粒對油膜壓力的影響，并得到如下結論：當顆粒的寬度在油膜厚度方向相同時，長寬比越大的顆粒對油膜壓力的影響也越大；當顆粒長軸相等時，顆粒在油膜厚度方向的寬度越大，則其對油膜壓力的影響也越大；而當顆粒的長度和寬度一定時，顆粒形狀對潤滑油流動的阻礙能力越強則顆粒對于油膜壓力的影響也越大。