主動后輪轉向汽車與轉矩分配協調控制研究

元加加，韓 偉，趙沛竹

（江西理工大學 機電工程學院，贛州 341000）

0 引言

轉向系統作為汽車底盤重要組成部分，提高汽車轉向特性對改善車輛操縱穩定性具有十分重要的作用，為此，研究人員提出了一些主動轉向技術來實現上述目標。目前采用四輪轉向系統來改善汽車操縱穩定性已成為了研究熱點[1]。如Hirche等[2]運用模糊控制對主動后輪轉向車輛的操縱穩定性進行研究，但制定模糊規則主要依賴設計者經驗。杜峰等[3]基于前后反饋設計線性二次型主動后輪轉向控制器，分析半正定矩陣中權重系數對控制器性能的影響。考慮路面附著變化對控制器的影響，謝憲毅等[4]引入變權重系數實現參數自適應調節，來提升最優控制器的性能及適用范圍。Zhang等[5]為提高車輛的橫擺穩定性，設計一種新型脈沖主動后輪轉向系統，經仿真表明能顯著提高車輛的橫擺穩定性。邱浩等[6]設計主動后輪轉向滑模控制器來跟蹤理想橫擺角速度，忽略了質心側偏角也會受后輪轉角影響。針對單一將橫擺角速度作為控制變量，Wagner等[7]設計一種基于主動后輪轉向的新型結構，來避免劇烈反向轉向時車輛可能出現運動姿態惡化的狀況。

為兼顧考慮兩者對車輛狀態的影響，基于線性車輛模型，以橫擺角速度和質心側偏角為控制變量，采用滑模控制理論設計后輪轉向控制器及車輛穩定控制器，提出一種主動后輪轉向與轉矩分配協調控制來提升車輛的操縱穩定性。為使模型驗證更具實際意義，在高/低附著路面分別進行閉環雙移線仿真驗證。

1 車輛橫向動力學模型

為更好地研究獨立驅動電動汽車的橫向動力學，采用簡化只有橫向和橫擺方向上運動的線性2自由度車輛模型。依據牛頓第二定律，建立其微分方程：

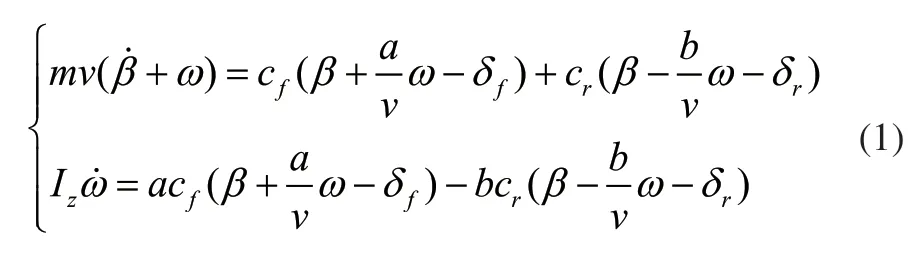
式中：m為整車質量；β為車輛質心側偏角；ω為橫擺角速度；v為質心縱向速度分量；Iz為繞質心的橫擺轉動慣量；cf，cr分別為前后輪等效側偏剛度；a，b分別為質心至前后軸距離；δf，δr分別為汽車前后輪轉角。

將前輪轉向車輛穩態橫擺角速度作為理想橫擺角速度。由于車輛的橫向加速度無法超過由地面所能提供的最大橫向加速度，同時考慮到瞬態響應過程存在純滯后特性的慣性環節，最終理想橫擺角速度表達式[8]可表為：

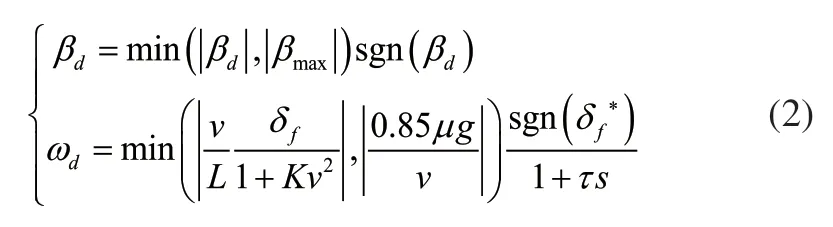
式中：βd為汽車理想質心側偏角，理想情況下可視為0。ωd為汽車理想橫擺角速度，L=a+b為汽車軸距，K稱為汽車穩定性因數，δf*為前輪轉向車輛前輪轉角，τ為慣性環節時間常數，經驗范圍一般為0.1s～0.25s。參考文獻[9]，本次試驗取0.2s。

2 滑模變結構控制器設計

2.1 主動后輪轉向控制器設計

為改善傳統車輛的轉向性能，設計以質心側偏角滑模變結構控制率為核心的后輪轉向控制器，通過控制后輪轉角，使得車輛質心側偏角趨近于理想質心側偏角βd。構造滑模切換面為：

選用具有趨近速度快且到達切換面附近速度小特點的指數趨近率：

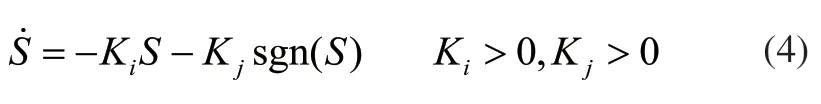
對式(3)求導，并聯合式(1)、式(4)可得滑模控制律表達式：

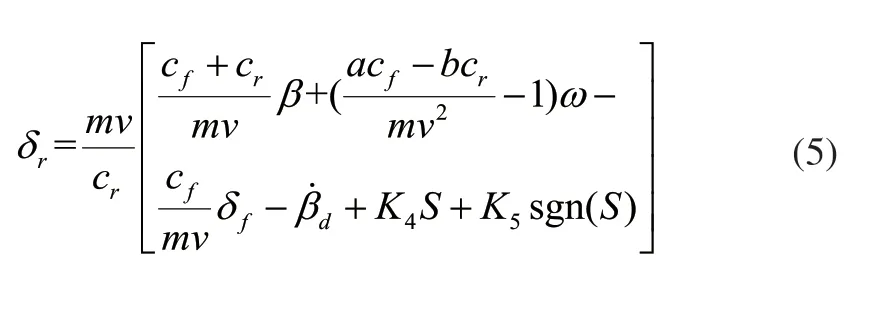
2.2 車輛穩定性滑模控制器設計

1）定義橫擺角速度控制的滑模切換面并求其導數：

對其求導，并聯合式(1)、式(4)，可得橫擺角速度控制的附加橫擺力矩為：

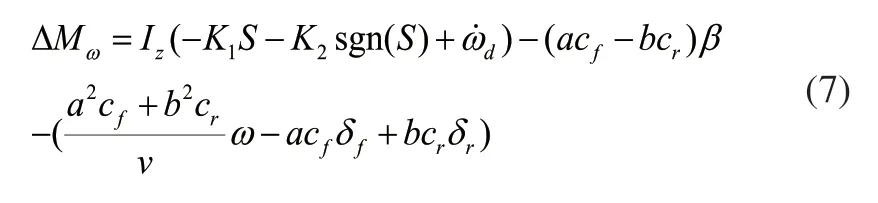
2）定義質心側偏角控制的滑模切換面為：

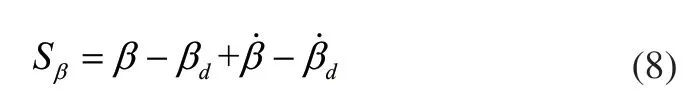
同理，可得質心側偏角控制的附加橫擺力矩為：

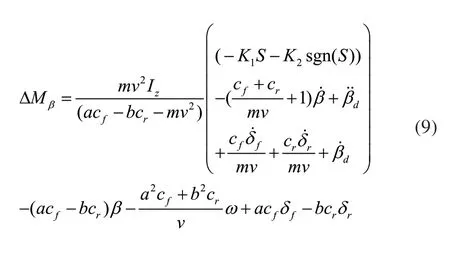
為實現橫擺角速度和質心側偏角的同時跟蹤，需按|β|的大小，對橫擺角速度控制輸出的ΔMω和質心側偏角控制輸出的ΔMβ進行加權協調。依據經驗式(10)來確定ε，權值系數依次為ε，1-ε。

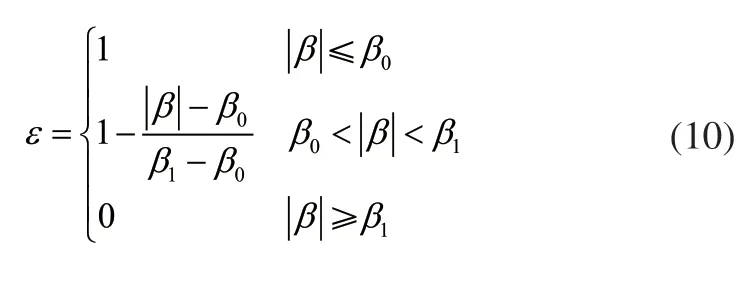
則控制器的最終輸出控制率為：

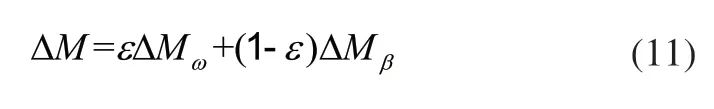
為削弱或避免因滑模面切換引起的抖振現象，將式(5)、式(7)、式(9)中的符號函數sgn（S）用飽和函數Sat（S）代替，飽和函數表達式[11]為：

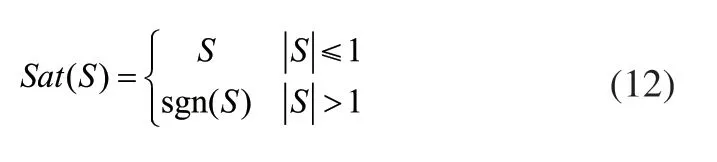
3 轉矩分配

考慮到實際需求，選用常見的平均分配[12]控制方法來對車輛穩定性控制。定義前后軸間的轉矩轉移量為：

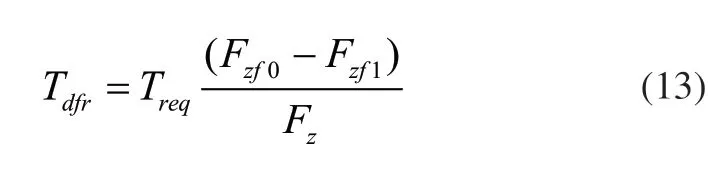
式中：Tdfr為前軸轉矩轉移量；Treq為駕駛員期望轉矩；Fzf0、Fzf1分別為實時狀態下前軸垂直載荷及靜止狀態下前軸垂直載荷；Fz為整車的垂直載荷。

車輛轉彎時，對于左右兩側車輪縱向力分配十分重要，應給予外側更多的縱向力。定義前后軸左右兩側車輪的轉矩轉移量為：

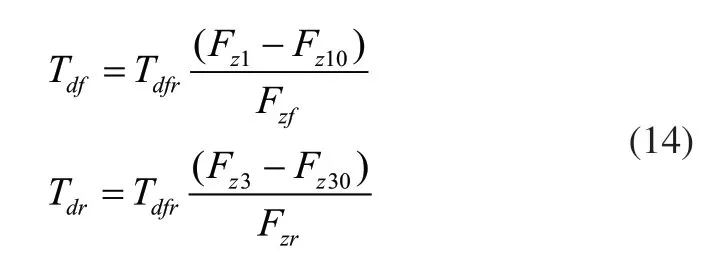
式中：Tdf、Tdr分別為前軸兩側車輪轉矩轉移量；Fz1、Fz10分別為實時狀態及靜止狀態下前軸左前輪垂直載荷；Fz3、Fz30分別為實時狀態及靜止狀態下后軸左后輪垂直載荷；Fzf、Fzr分別為實時狀態下前后軸垂直載荷。

最終的轉矩分配策略如下：

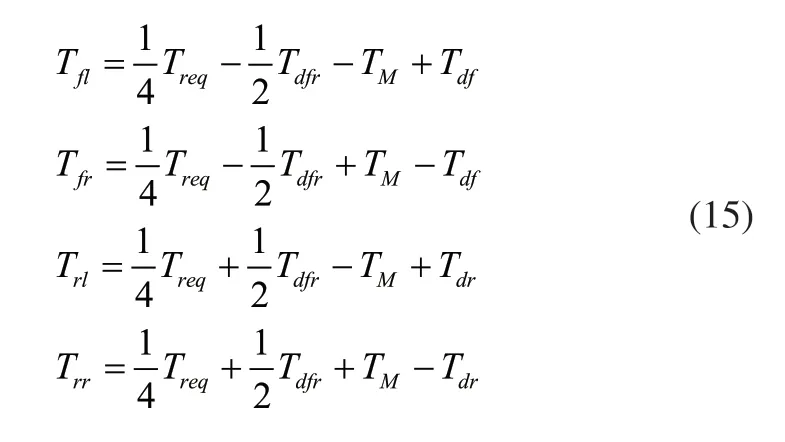
式中： Tij依次為左前輪、右前輪、左后輪及右后輪的驅動轉矩；Treq為駕駛員期望轉距；TM為附加橫擺力矩ΔM傳遞到每個車輪的轉矩。

4 仿真驗證

選用七自由度整車模型為試驗模型，搭建“人-車-路”閉環控制系統，如圖1所示，用于對控制系統的閉環仿真研究。其中駕駛員模型采用郭孔輝院士提出的最優側向加速度駕駛員模型[13]，系統輸入為前方道路信息f（t），輸出為車輛的側向位移，以此反映汽車軌跡跟蹤的精度。

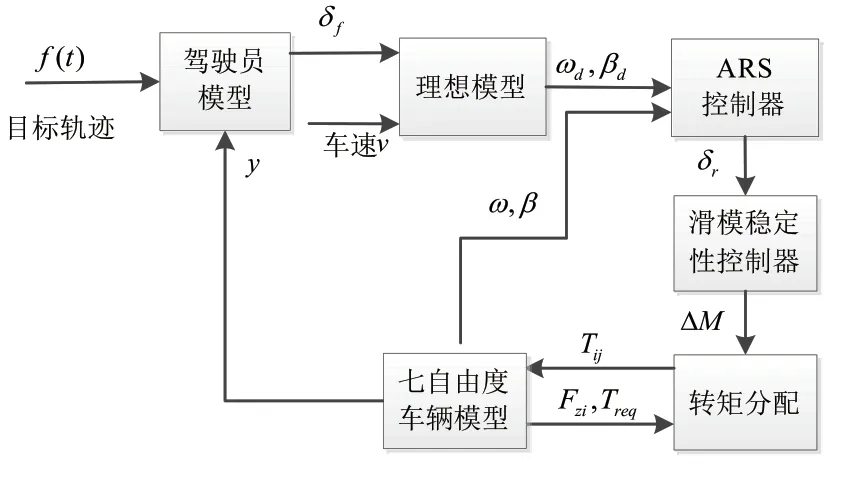
圖1 “人-車-路”閉環控制系統

本次仿真試驗中駕駛員模型神經反應滯后時間取Td=0.25s，操縱反應滯后時間為Th=0.1s，駕駛員預瞄時間選取Tp=0.75s，傳動比i=17.5，采用的是2.5階跟隨，即跟隨階數α=0.5。試驗工況選用雙移線工況，并按ISO/TR3888規定設計標準緊急雙移線試驗道路，來模擬車輛在實際道路上進行超車或緊急避障情況。為凸顯對比效果，同時進行了同條件下等結構參數的無控制前輪轉向和前饋比例控制[14]四輪轉向車輛仿真試驗。為便于分析，特將滑模控制主動后輪轉向與轉矩協調控制簡稱“滑模控制”，類比依次可得“無控制”及“比例控制”。分別以恒定20m/s速度在高/低附著路面條件下進行仿真試驗，車輛主要參數參考文獻[15]，相關參數取值為Iw=1.2（kg.m2），R=0.359m，B=1.6m，hg=0.59m，分別代表車輪轉動慣量、車輪滾動半徑、軸距及車輛質心高度，K1、K2、K4、K5為滑模控制參數，分別取值為0.2、0.2、10、15。

如圖2(a)可以看出，當車輛以車速為行駛在高附著路面時，3種轉向控制系統均能較好完成目標軌跡的跟蹤。由圖2(b)可知，三種控制方式的橫擺角速度與理想值存在明顯相位差，這是由于延時模塊存在引起的。相比較之，滑模控制車輛橫擺角速度跟蹤效果最佳。從圖2(c)可見，滑模控制車輛質心側偏角變化近乎一條值為零的直線，其余控制方式車輛的質心側偏角均有明顯的變化。表明滑模控制車輛進行換道過程中車身姿態保持最好，完成對理想質心側偏角的跟蹤，提升了車輛的轉向性能。在圖2(d)質心側偏角相圖中，相對比可知，滑模控制車輛相圖變化范圍近似一點，其相圖軌跡始終處于相平面較小地穩定范圍，且最終收斂，說明滑模控制車輛具有較高的穩定性。

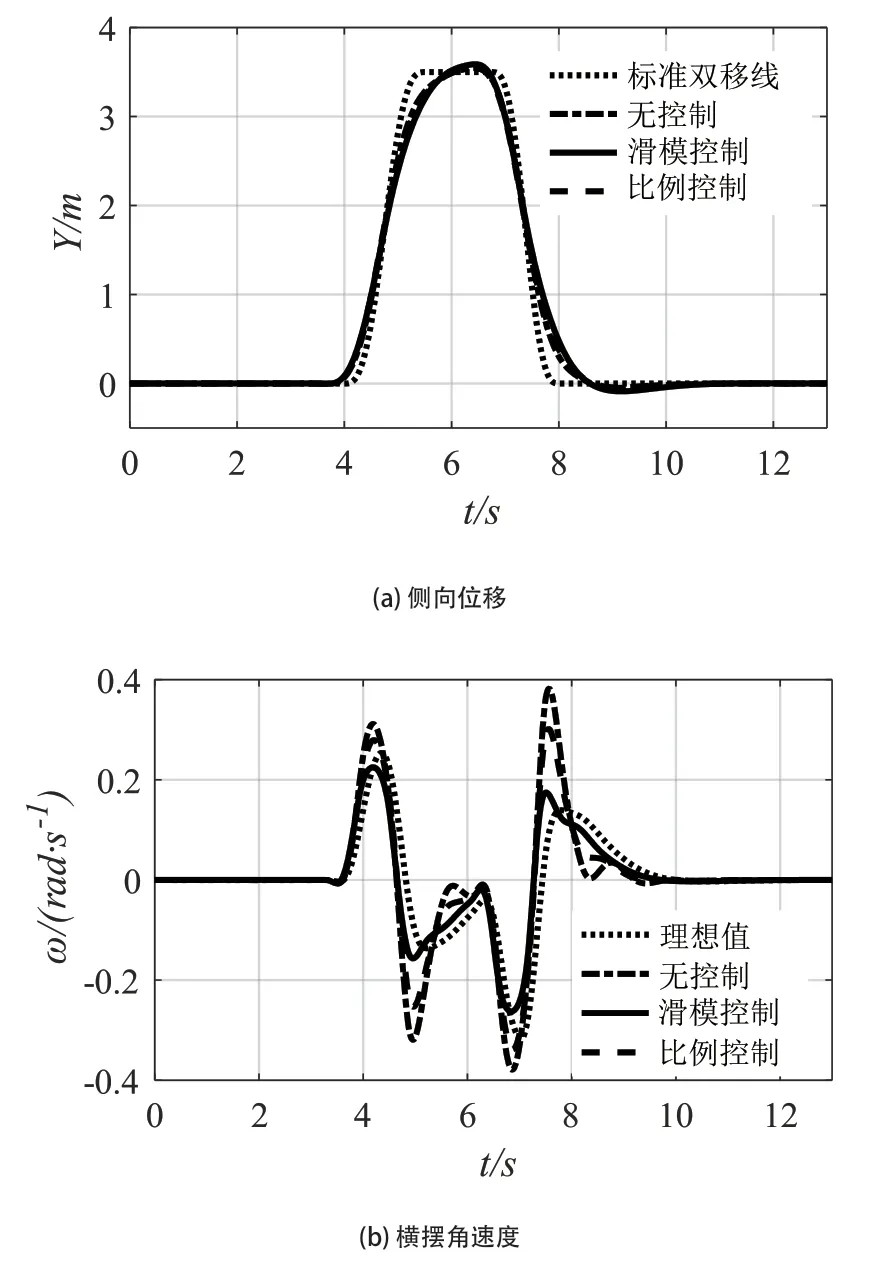
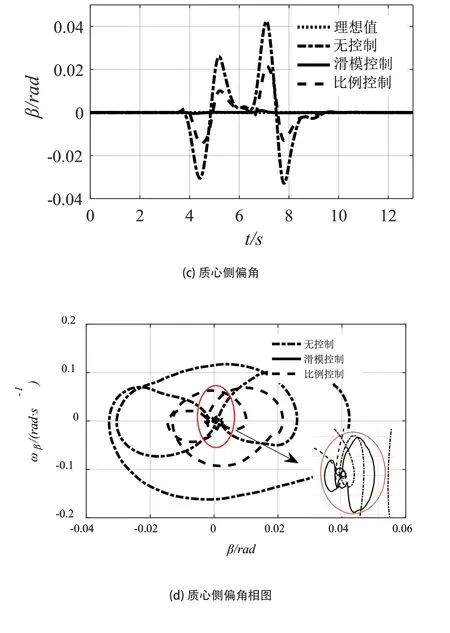
圖2 高附路面閉環仿真結果

圖3為車輛以車速為20m/s行駛在低附著路面時的仿真結果。圖3(a)可看出，無控制車輛已出現失穩情況，有控制的車輛依舊能完成變道任務，且沒有出現失穩情況。雖車輛軌跡跟蹤誤差較大，這是由于在極限工況下，車輛所能達到的系統增益受限及車輛本身的非線性造成的。兩者對比，滑模控制車輛較快地調整過來，軌跡跟蹤誤差更小。由圖3(b)可知，滑模控制車輛始終能較好跟蹤理想橫擺角速度，過渡較為平順，轉向比較平穩，而無控制車輛的橫擺角速度軌跡發散。此外，從如圖3(c)和圖3(d)可知，無控制車輛的質心側偏角軌跡發散，其相位曲線圖最終也并未收斂，表明車輛最終處于失穩情況。有控制車輛質心側偏角可維持在一定范圍內，并最終收斂。滑模控制車輛的質心側偏角近似于一條為零的直線，且其相位曲線軌跡范圍最小，車輛始終處于穩定狀態，可使得駕駛員獲取較好的車輛轉向特性。

5 結語

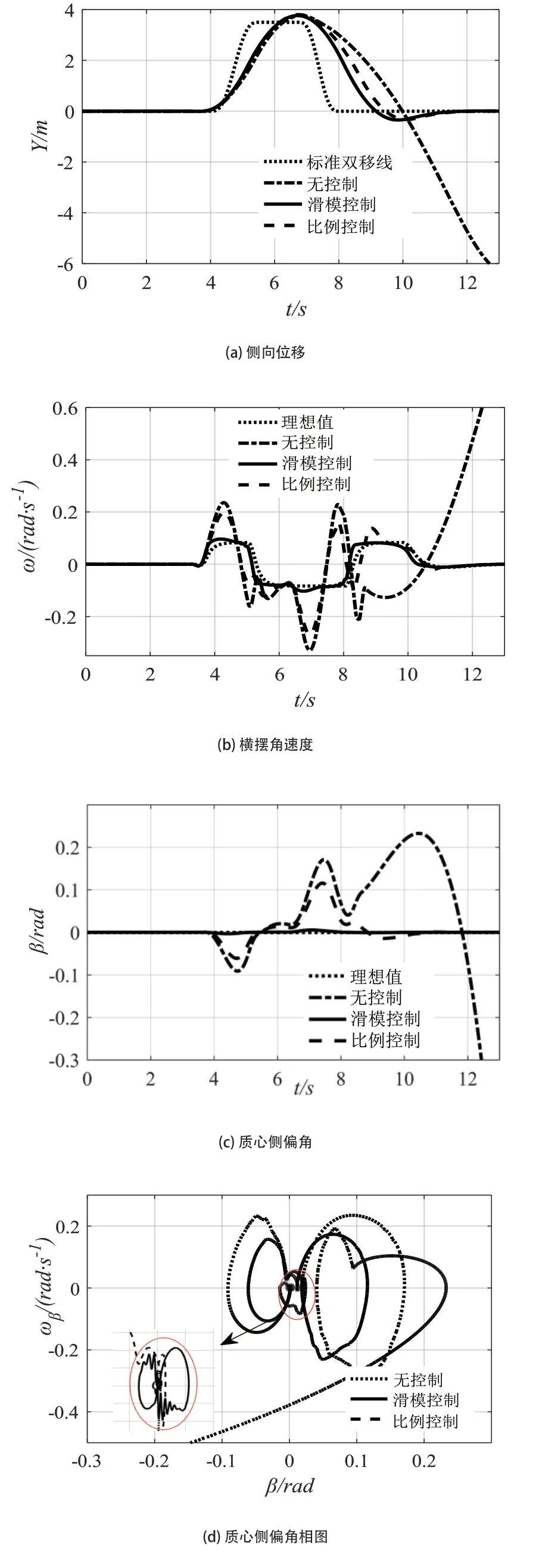
圖3 低附路面閉環仿真結果

基于線性車輛模型利用滑模變結構設計后輪轉向控制器和車輛穩定性控制器，借用Simulink完成駕駛員模型、非線性整車模型等模塊的搭建，以及標準雙移線試驗道路軌跡的設計，構建“人-車-路”閉環控制系統。經試驗仿真表明：所設計的主動后輪轉向車輛在高/低附著路面均具有較好的轉向姿態，且能較好完成軌跡跟蹤。特別地，在低附著路面完成始終跟隨理想質心側偏角的同時，還具有更高的穩定性，對車輛的操縱穩定性具有較好的改善。