橫流轉捩模型參數不確定度量化分析與應用研究

向星皓，張毅鋒，陳堅強,2，袁先旭,2，陳樹生

(1. 中國空氣動力研究與發展中心空氣動力學國家重點實驗室，綿陽 621000；2. 中國空氣動力研究與發展中心計算空氣動力研究所， 綿陽 621000；3. 西北工業大學航空學院，西安 710072)

0 引 言

邊界層轉捩通常是指邊界層流動由層流狀態發展為湍流狀態的過程，是一個多因素耦合影響、包含復雜轉捩機理的物理現象[1]。真實飛行器的三維邊界層轉捩往往由橫流轉捩主導[2]。作為轉捩預測手段之一的轉捩模型在構造過程中涉及到較多模型參數，大部分參數是通過特定條件下的風洞實驗和理論分析來確定的，其適用范圍有限，在實際應用中往往需要針對不同流動類型進行參數調整。

由于實驗數據獲取困難以及缺乏對轉捩機理的深入理解，在轉捩模型的構造過程中存在一定的認知不確定性。雖然該不確定性會隨著人們對物理模型了解的深入和實驗數據的豐富而逐步減小，但是目前仍會導致模型參數不確定性。這主要體現在給定的模型參數未必最優，針對具體轉捩類型與流場特性，需要對參數進行標定與修正。

模型參數的標定通常是確定性的，給出了參數具體取值或取值范圍。如文獻[3]用特定工況的理論分析和風洞實驗，結合建模中的部分假設直接確定模型參數取值。也有采用類似試錯法進行參數調整，如Lien等[4]在建模以后對參數進行變參數調整優化，在特定算例中對模型參數進行試錯調整，實現一個較小范圍的參數最優。

不確定度量化分析相比以往確定性的參數標定，能夠提供多參數對轉捩起始位置耦合作用的定量影響[5]、能夠定量給出計算結果不確定度范圍以及所需樣本量小[6]等諸多優勢，對于參數標定工作以及模型參數效能分析具有重要的指導意義。不確定度分析具有非侵入式以及對隨機輸入變量具有指數收斂性的特點[6]，能夠提供輸入條件對轉捩起始位置的定量影響[5]。

由于認知不確定性造成的轉捩模型參數不確定性因素普遍存在，不確定度量化分析就顯得尤為必要。張涵信院士等[7]指出，CFD方法的不確定度或可靠性一直以來都是CFD中需要特別關心的問題。不確定度量化分析對于轉捩模型參數研究具有重要意義，能夠提供參數敏感性以及不確定度的定量結論，進而對參數效能研究以及模型參數的篩選調試提供具體有效的指導。在此基礎上，不確定度量化分析方法可以甄別對計算結果影響大的關鍵因素，為轉捩模型的改進指明方向。

在轉捩/湍流模型的不確定度量化分析方面，目前關于模型不確定度研究主要集中在湍流模型方面，對于轉捩模型的不確定度研究則相對有限。Pecnik等[5]對由于自由來流不確定性與可壓縮修正所導致的轉捩模型不確定度進行了分析，分析發現上述因素對轉捩起始位置與氣動熱分布的不確定度造成顯著影響。Zhao等[8]對轉捩模型在高超聲速平板和尖錐中的不確定度和參數敏感性開展研究，采用非嵌入式多項式混沌(Non-intrusive polgnomial chaos,NIPC)方法對γ-Reθt和k-ω-γ轉捩模型進行了基于來流不確定性的不確定度量化分析。

傳統不確定度分析方法如工程應用較為普遍的蒙特-卡洛(Monte-Carlo)方法，在對計算流體力學氣動力、熱不確定度分析時，樣本需求量大，計算資源消耗大[9]。相對于蒙特-卡洛方法而言，非嵌入式多項式混沌(NIPC)方法不需要修改求解器，具有計算量小、收斂快的特點，在復雜模型、系統的不確定度量化分析中得到廣泛應用[10]。

本文首先基于課題組Chant 2.0計算平臺[11]實現了當地化橫流轉捩模型[12-13]，然后采用非嵌入式多項式混沌方法對NLF(2)- 0415后掠翼和S-K低速平板進行了模型參數不確定度量化分析和參數敏感性分析，得到了當地化的橫流轉捩模型參數不確定性的定量分析結果。以分析結果為指導對橫流轉捩模型進行了重新標定與參數修正，最后將修正的轉捩模型在NLF(2)- 0415后掠翼、6:1標準橢球體和DLR-F4翼身組合體算例中進行了驗證。計算結果表明，重新標定的模型對于亞聲速、跨聲速情況下的三維邊界層轉捩具有較好適用性。

1 計算方法

1.1 控制方程

本文采用有限體積法對雷諾平均Navier-Stokes(RANS)方程進行求解，無黏通量計算格式為AUSMPW+，無黏項離散格式為二階精度NND格式，黏性項離散格式為二階中心差分格式，時間推進采用LU-SGS方法，湍流模型采用k-ωSST模型，采用MPI技術進行大規模并行計算。

1.2 橫流轉捩模型的不確定度輸入參數選取

本文在Chant 2.0計算平臺實現了文獻[12-13]提出的當地化橫流轉捩預測模型。由于計算平臺差異，模型參數需要重新標定。對模型開展了轉捩相關量不確定度量化分析和參數研究，以指導參數標定工作。橫流模型基于γ-Reθt轉捩模型進行拓展，橫流效應是通過在原始模型的Reθt輸運方程中增加橫流源項來實現的。

(1)

(2)

(3)

cCF=0.6

(4)

在橫流源項DSCF中有兩個模型參數作為橫流源項的系數而存在，分別是cCF和cθt。上述參數大小會直接影響輸運方程中的橫流源項大小，影響模型預測的橫流轉捩起始位置，是橫流轉捩不確定性研究的重點關注參數。

物面粗糙度作為物體表面固有屬性參數，在大多數風洞實驗、飛行試驗以及CFD橫流模型預測中，這一重要參數往往是缺省的，或者測量存在一定的誤差。在本文所用的橫流轉捩模型中，表面粗糙度h是定常橫流轉捩判據ReSCF的重要參數之一，見式(5)。本文將粗糙度h作為輸入參數之一進行不確定度和參數敏感性分析。

319.51+f(+ΔHCF)-f(-ΔHCF)

(5)

綜上所述，本文選取模型參數cCF和cθt以及表面粗糙度h進行不確定度與參數敏感性分析，對模型參數進行篩選與橫流標定。橫流轉捩模型的其余參數則與γ-Reθt模型一致，見文獻[12]。

1.3 不確定度分析方法

傳統的CFD數值模擬具有確定性，即針對一個確定的問題通過一組確定性的輸入從而得到一個確定性的計算結果[10]。對于轉捩模型而言，由于轉捩機理的高度復雜性和在風洞實驗和飛行試驗中測量的困難，以及對模型認知存在的局限，導致構建的轉捩模型的參數也存在較大不確定性[11]。因此有必要針對轉捩模型參數所導致的轉捩起始位置和轉捩特征量的預測不確定性進行不確定度量化分析。

本文采用非嵌入式多項式混沌方法進行不確定度量化分析。在CFD轉捩預測模型不確定度分析中，以壁面摩擦力系數Cf、轉捩起始位置等重要參數作為隨機輸出變量，表示為：

(6)

式中:α*是CFD直接計算結果，αj(x)是計算結果的確定部分耦合系數，ψj(ξ)是計算結果的隨機部分。ξ=(ξ1,…,ξn)是n維隨機變量，而隨機部分ψj(ξ)是以隨機變量ξ為自變量的隨機函數，為ξ的正交多項式。

隨機函數ψj(ξ)根據隨機變量的ξ分布，即本文輸入的轉捩模型參數的分布類型不同而有所區別，對應選取不同形式的正交多項式。若模型參數滿足均勻分布時，正交多項式選擇Legendre正交多項式；若模型參數滿足正態分布時，正交多項式選取Hermite正交多項式[9]。

對多項式采取p階截斷，設隨機參數的維數為n，則混沌多項式(PCE)項數可以表示為：

(7)

本文選取隨機響應面法求解混沌多項式系數，開展不確定度分析。參數樣本量的設置，參考文獻[14]選用PCE系數兩倍的過采樣方法。根據Schaefer等[15]的比較結果，采用精度和收斂性均表現較好的拉丁超立方(LHD)抽樣方法，對模型參數進行抽樣選取。

選取了Nt個隨機樣本點后，每一個樣本點對應一個確定的CFD計算結果，由式(6)可得[9]：

(8)

采用最小二次回歸對PCE系數αi進行求解[9]，平均值μ和方差D按如下計算：

μ=α0(x)

(9)

(10)

每一個輸入參數變量i對輸出變量不確定度貢獻的相對大小是通過敏感性指數來表征的。Sobol指數(STi)作為敏感性指數定義為部分方差與總方差的比值[16]：

(11)

其中部分方差與總方差分別為：

(12)

(13)

針對輸入參數i的Sobol指數(STi)則定義為包含變量i的所有部分Sobol指數之和：

(14)

2 不確定度與參數敏感性分析

本文選取S-K低速平板和NFL(2)- 0415后掠翼兩個算例進行不確定度量化和參數敏感性分析。第一個算例的邊界層轉捩由T-S波主導，第二個算例是由橫流不穩定性主導。通過上述兩個算例的NIPC分析，能夠得到模型參數在不同轉捩類型中的效能，從而進行有針對性的參數修正工作。

選取三個模型參數作為輸入，選取兩個物理量作為輸出響應，進行不確定度量化分析。兩個輸出響應為：轉捩起始位置xtr和壁面摩擦力系數Cf。三個輸入參數及依據為：1)動量厚度雷諾數輸運方程中橫流破壞項系數參數cCF,該參數作為橫流耗散項DSCF系數(見式(2))，對模型的橫流轉捩預測影響較大；2)表面粗糙度h，該參數構成橫流轉捩判據ReSCF迭代式，必然對橫流轉捩產生影響；3)γ-Reθt轉捩模型和橫流模塊DSCF項共有的系數參數cθt。

上述三個參數對橫流轉捩存在重要影響是顯而易見的，本文目的主要在于采用NIPC方法對參數影響進行定量分析，得出不確定度和參數敏感性的定量結論，進一步指導參數標定工作。

輸入參數的不確定度范圍設置如下：橫流參數cCF基準值根據文獻[13]設置為原始值0.6，正負偏差百分比根據模型標定經驗[17]設置為±66.66%，對應參數變化范圍[0.2，1.0]；參數cθt基準值設置為0.03[12]，不確定度正負偏差百分比為±20%，對應參數變化范圍[0.024，0.036]；表面粗糙度h根據機加工精度覆蓋從不可辨加工痕跡的超級加工光澤面至粗糙漆面[13,18-19]，粗糙度變化范圍為[0.5，10]，單位μm。

混沌多項式(PCE)采用2階截斷，根據式(7)采用過采樣方法，選取樣本數為20，采用拉丁超立方進行抽樣，選擇轉捩起始位置和壁面摩阻系數作為輸出響應。在95%的置信區間下，轉捩起始位置與摩阻系數Cf輸出響應的不確定度為UQ%=100×1.96σR/μR。

2.1 S-K低速平板算例

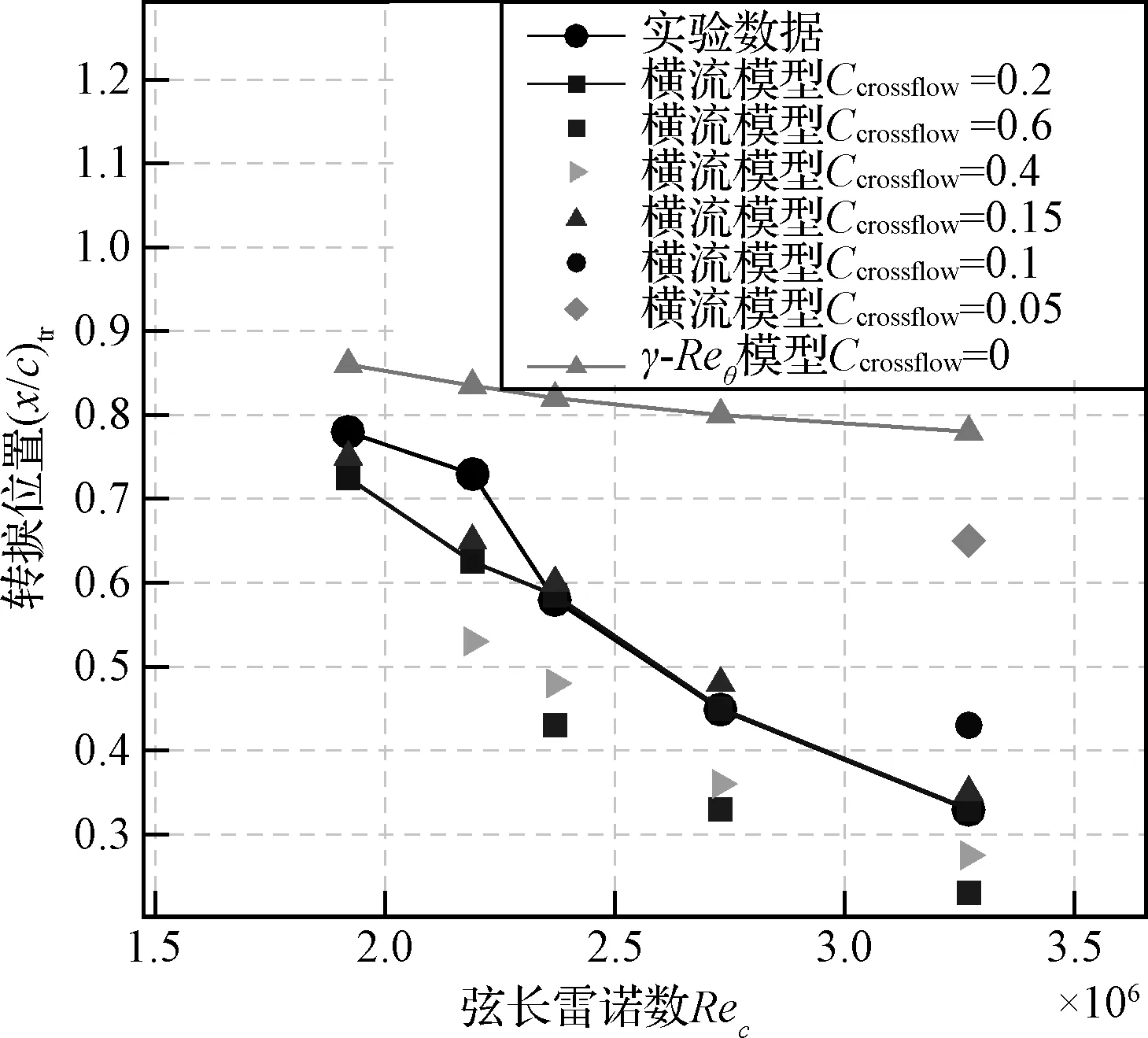
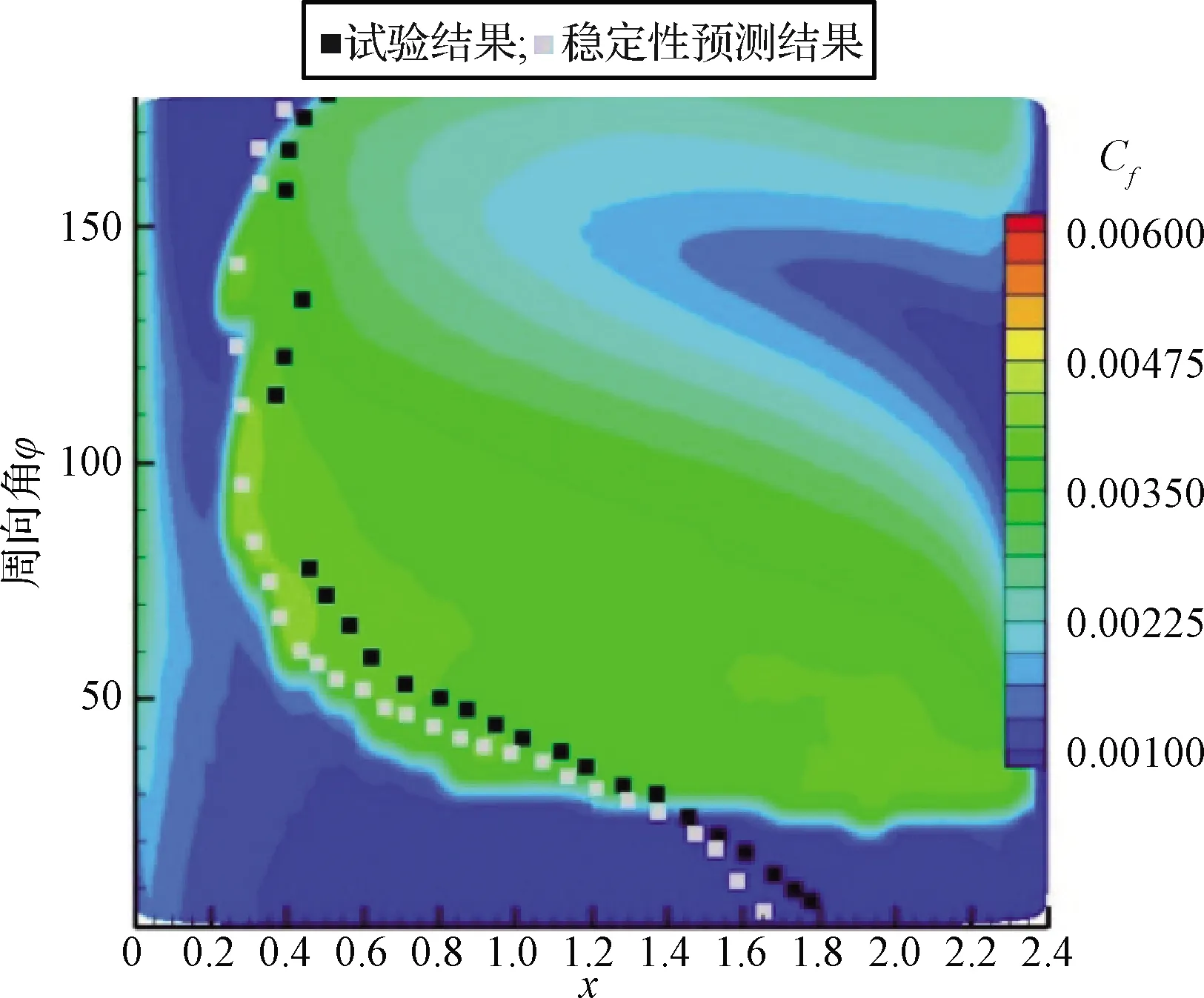
S-K低速平板來流狀態為Ma=0.147,Re=3.34×106/m,來流湍流度Tu∞=0.18%。以摩阻系數Cf為輸出響應進行了基于三參數的不確定度與參數敏感性分析，通過不同站位上三個輸入參數對應的敏感性指數比較，可以觀察輸入參數在不同流動過程的影響程度。由圖1可知，在轉捩區(0.8

圖1 低速平板算例壁面Cf不確定度與參數敏感指數Fig.1 UQ% & sobol index of Cf in S-K flat plate

與摩阻系數類似，以轉捩起始位置為輸出響應也可以給出三個參數的敏感性指數，計算結果見表1，模型參數cθt的敏感性指數大約是參數cCF與物面粗糙度h的敏感性指數的2倍，與圖1的結果一致。在相對幅值變化相同的條件下，參數cθt所引起的轉捩起始位置xtr的變化同樣更為顯著。

表1 低速平板算例轉捩起始位置的三參數敏感性指數Table 1 Sobol index in S-K flat plate case

該算例說明，cθt是影響T-S不穩定性主導轉捩計算的主要參數，調整模型參數cθt獲得的敏感性高于其他兩個參數，在對流向轉捩進行標定時，應主要考慮參數cθt。

2.2 NFL(2)- 0415后掠翼算例

2.2.1模型參數不確定度量化

NFL(2)- 0415后掠翼上表面轉捩過程由橫流不穩定性主導，選取上壁面摩阻系數Cf和轉捩起始位置xtr作為輸出響應進行分析。不確定度分析的NFL(2)- 0415后掠翼算例計算狀態為攻角-4°,Ma=0.2，Re=3.27×106/m，來流湍流度Tu∞=0.09%，邊界層遠場湍流度自由衰減至Tu≤0.02%。

圖2是所有拉丁超立方抽樣樣本的上表面摩阻系數Cf分布圖，并給出NIPC均值進行對照。在20個樣本曲線中，轉捩起始位置在x=0.43附近有5條Cf曲線基本重合，對應樣本編號為7,12,13,19,20(見表2)。它們中的參數cCF與參數h有此消彼長的關系，說明兩參數對橫流轉捩的影響作用近似。

圖2 采樣樣本的上壁面Cf分布圖Fig.2 Cf distribution of all samples

表2則是采用拉丁超立方抽樣歸一化參數樣本(參數樣本：最大值→1，最小值→-1)。該不確定度分析手段具有“樣本量小、信息豐富”的特點。與常規變參分析進行對比，若采用常規單參數調試的方法，假設每個參數在指定范圍內進行六個均勻采樣，則在樣本量相當的情況下，傳統方法只能得到單參數調試結果，無法得到參數耦合變化下的不確定度與參數敏感性分析結果(見圖3、圖4)。

表2 拉丁超立方抽樣輸入參數及轉捩起始位置Table 2 LHD sampling and transition location

圖3是基于參數抽樣結果的壁面摩阻系數均值及誤差帶分布。其意義在于僅采用了少量樣本，即提供了變參數橫流轉捩模型輸出量的整個空間分布及其變化范圍。如采用傳統變參分析，其參數樣本量與計算量將遠大于此。

由圖3可知，在x<0.4的層流區和x>0.7以后的充分發展湍流區，誤差帶范圍明顯低于在0.4

圖3 NIPC方法壁面摩擦系數均值及誤差帶分布Fig.3 Surface Cf distribution with NIPC method

圖4 后掠翼算例Cf不確定度與參數敏感指數分布Fig.4 UQ & Sobol Index of Cf on back-swept wing

將上述參數采樣和對應計算結果作為輸入與輸出，采用NIPC方法進行不確定度分析。圖4為摩阻Cf作為輸出響應的不確定度與參數敏感性指數沿弦向分布，敏感性在第2.2.2節進行分析。不確定度的分布與圖3誤差帶區間分布具有一致性，在x<0.4與x>0.7的區間近似為0，在轉捩區間呈現出“兩端小、中間大”的分布規律。轉捩區域中x/c=0.43時Cf不確定度達到最大，大小約為189%。

2.2.2模型參數敏感性分析

對轉捩起始位置xtr和壁面摩擦系數Cf分布分別進行了參數敏感性的點分析和線分析。二者反映不同物理量對參數變化的敏感程度，轉捩起始位置三參數點分析的敏感性指數(見表3)，不能通過壁面摩擦系數敏感性指數分布(見圖4)直接得到。

以轉捩起始位置xtr為輸出響應，進行參數敏感性的點分析。表3給出了經不確定度點分析的轉捩起始位置敏感性指數，三參數的Sobol指數分別為0.56153，0.43323，0.12676，該指數表征參數敏感程度，參數cCF與h的敏感性指數約為參數cθt敏感性指數的3～4倍，其對橫流轉捩起始位置的影響要遠大于參數cθt。

表3 后掠翼轉捩起始位置的三參數敏感性指數Table 3 Sobol index in back-swept wing case

以摩阻Cf為輸出響應，進行參數敏感性的線分析見圖4。從圖4可以看出，對轉捩區間Cf分布影響較大的參數是cCF與表面粗糙度h，其敏感性指數在轉捩區域內(0.40.8的區間，cθt的敏感性指數趨于0，即cθt幾乎不影響轉捩前的層流區域和轉捩后的湍流區域的Cf分布。但cCF,h與cθt的敏感性指數規律不同，它們僅在x<0.4的層流區域近似為0，在x>0.8轉捩完成以后的湍流區域，cCF敏感性指數約為0.3，h的敏感性指數約為0.4。說明橫流參數cCF與表面粗糙度h不僅影響轉捩起始位置，還會對轉捩之后的Cf分布造成一定影響。與該觀點相互印證的是圖3中誤差帶分析結果，x∈[0.8,1]區域內誤差帶不為零，該區域內的不確定度大約在4%～8%的范圍內。調整參數cCF和h，能使轉捩起始位置相對于流向轉捩提前發生，模擬橫流轉捩效果。

2.3 不確定度與參數敏感性分析小結

相比常規變參分析方法，不確定度量化分析方法具有如下顯著優勢：

1) 不確定度量化分析能夠給出研究者所關心的輸出物理量的不確定度定量范圍，具有重要的工程指導意義。

2) 不確定度量化分析所給出的參數敏感性指數，可以直接量化參數在特定空間位置對特定物理量的影響大小，而常規變參分析只能給出影響大小的宏觀定性排序。前者對于參數篩選與標定工作更具指導意義。

3) 基于NIPC的不確定度分析，采用拉丁超立方抽樣需要的樣本量小，得到的信息豐富，效費比高，能夠綜合考慮多參數耦合變化時的參數作用效應。常規變參數分析不具備上述特點。

三輸入參數以不同的作用方式都對轉捩模擬結果有影響，不同的轉捩方式需采用不同的參數進行標定：

1) 參數cθt對流向轉捩相關量的不確定度影響較大，敏感性較高，且對于橫流轉捩影響較小。流向轉捩模型的標定應主要針對參數cθt開展。

2) 參數cCF對橫流轉捩相關量的不確定度影響較大，敏感性較高，且cCF對于流向轉捩影響較小，對橫流模型的標定應主要針對參數cCF開展。

3) 表面粗糙度h是反映模型加工表面光潔程度的固有參數，對橫流轉捩位置xtr以及Cf分布均存在顯著影響。不同風洞實驗、飛行試驗的模型表面由于加工精度不同，粗糙度差別較大，需要對其精確測量。

3 橫流轉捩模型參數標定與校驗

本文主要研究橫流轉捩模型參數，根據不確定度和參數敏感性分析結果，對模型參數進行篩選，給出參數cCF的標定和校驗結果。

3.1 橫流模型參數標定

針對不同計算平臺的模型參數標定的廣泛需求，以不確定度和參數敏感性分析結果為指導，進行模型參數篩選和標定。

NFL(2)- 0415后掠翼算例來流狀態為Ma=0.2,Re=1.9～3.3×106/m (1.93×106, 2.19×106, 2.40×106, 2.73×106, 3.27×106)。在Chant 2.0計算平臺上采用基準參數的橫流模型，由于計算平臺差異，采用原始基準參數的模型預測的NFL- 0415(2)后掠翼轉捩起始位置與實驗結果偏差較大，如圖5所示。在雷諾數為3.27×106算例中轉捩起始位置偏差大約在30%以上。根據現有的NFL- 0415后掠翼轉捩實驗數據[19]，采用改變模型參數值的方法調整橫流轉捩起始位置，對橫流轉捩模型進行重新標定。表面粗糙度設置為實驗測量結果[13,19](h=3.3 μm)。

圖5 基準參數模型預測轉捩起始位置與實驗對比Fig.5 Transition location of modeling and experiment

由第2節不確定度與參數敏感性分析結果可知，在橫流不穩定性主導的轉捩中，模型參數cCF和cθt均影響轉捩位置，但cCF的參數敏感性指數更高(見表1和圖4)。同時cCF僅是動量厚度輸運方程橫流源項系數，該系數的調整與橫流轉捩位置變化具有單調一致性。因此選取參數cCF進行橫流標定。

雖然常規變參分析可以選取橫流耗散項DSCF系數cCF進行直接標定，但參數選取及變參數調試缺乏定量的誤差帶和敏感性數據支持，經驗性較大。

圖6 變參數的后掠翼的計算和實驗結果[19]Fig.6 Experiment & modeling results with varying parameter values[19]

就參數cCF對輸運方程的影響進行定性分析：該系數越小，Reθt輸運方程橫流破壞項占比越低，由間歇因子輸運方程啟動項對Reθt的單調性，減小該系數使轉捩起始位置后移。極限情況下cCF參數為0，橫流模型恢復至原始γ-Reθt轉捩模型。

根據上述分析以及圖3的采樣樣本結果，以表1樣本17, 3, 8為參考，設置參數cCF的標定范圍為[0，0.6]，選取cCF=0, 0.05, 0.1, 0.15, 0.2, 0.4, 0.6七個參數值在雷諾數Re=3.27×106算例中進行精細化標定。參數值取0.2時與實驗數據擬合最為準確，進一步在較大雷諾數范圍進行測試，表面粗糙度h=3.3 μm，Re=2.37×106與Re=3.27×106的轉捩起始位置偏差都得到了有效修正，轉捩起始位置與風洞實驗符合較好(見圖6)。

3.2 橫流轉捩算例

前文基于固定粗糙度的后掠翼算例對橫流模型參數進行了標定，本節對三種粗糙度、不同雷諾數條件下的后掠翼以及15°攻角橢球體和DLR-F4翼身組合體進行計算，以驗證橫流模型參數的適用性。

3.2.1NLF(2)- 0415后掠翼

NFL(2)- 0415無限展長后掠翼在-4°攻角下，機翼上表面的轉捩由橫流不穩定性主導，是低速橫流轉捩典型算例。選取該算例，采用標定后的模型對變粗糙度的風洞實驗[19]轉捩位置進行預測，驗證模型在不同粗糙度下橫流轉捩模擬能力。攻角為-4°，后掠角45°，雷諾數范圍為Re=1.9×106～3.8×106，網格量約50萬，物面第一層網格法向間距y+<1，壁面粗糙度(h)根據風洞模型加工精度設置為0.5 μm,3.3 μm,9 μm，來流湍流度Tu∞≈0.1%，νt/ν=5，前緣邊界層遠場湍流度Tu≤0.02%。

圖7是三種粗糙度、多雷諾數條件下的計算結果，預測的轉捩起始位置隨粗糙度和雷諾數變化規律與風洞實驗相同，粗糙度促進轉捩，增大雷諾數轉捩靠前。高雷諾數下模型預測的轉捩起始位置和實驗符合較好，低雷諾數下預測的轉捩起始位置相比實驗值靠前。

圖7 不同粗糙度下NFL- 0415后掠翼的實驗 和計算結果對比[13,19]Fig.7 Modeling and experimental results of different surface roughness values[13,19]

3.2.2帶傾角的標準橢球體

采用6:1標準橢球體[20]對重新標定的橫流模型在大攻角條件下的橫流轉捩預測能力進行驗證。算例選取攻角15°、雷諾數6.5×106的典型狀態進行測試。網格量為200萬，物面第一層網格法向間距y+<1。來流湍流度按衰減公式[12]進行設定，保證靠近橢球體的來流Tu≈0.1%，黏性比νt/ν=5，壁面粗糙度取默認值[13]h=3.3 μm。

圖8為實驗測量以及模型預測的橢球體表面摩阻系數分布云圖。圖8由上至下依次是實驗結果、γ-Reθt計算結果、Chant平臺橫流模型計算結果以及文獻計算結果[13]。在高雷諾數、大攻角且橫流不穩定性占主導的情況下，原始γ-Reθt模型的預測轉捩陣面與實驗存在較大差別，而Chant平臺標定后的橫流模型能較準確預測橢球表面的橫流轉捩陣面，轉捩區Cf值比實驗結果偏低，與文獻橫流模型[13]預測能力相當。圖9為沿長軸周向展開后的摩阻系數分布，轉捩模型預測橫流轉捩陣面與穩定性分析和風洞實驗符合較好。

圖8 橢球體表面摩擦系數分布云圖Fig.8 Cf contours on spheroid

圖9 Chant平臺橫流模型模擬表面摩擦力云圖Fig.9 Cf contour on spheroid: Chant modeling, stability theory and experimental result

3.2.3DLR-F4翼身組合體

DLR-F4翼身組合體是在歐洲跨聲速風洞中進行的實驗。風洞實驗[21]采用溫敏漆技術顯示層/湍流區域以及轉捩位置。圖10、圖11中實驗照片的明暗界線即為轉捩位置。風洞實驗Ma=0.785，機翼上表面為跨聲速流動區域。翼面有轉捩發生，上翼面靠近翼根部分的轉捩由橫流不穩定性主導，靠近翼尖區域的轉捩由T-S不穩定性主導。選取兩個攻角狀態：-2.59°，-0.87°，雷諾數Re=6×106，網格量約為320萬，物面第一層網格法向間距y+<1，來流湍流度Tu∞≈0.1%，保證邊界層遠場湍流度自由衰減至Tu≤0.05%，黏性比νt/ν=1，表面粗糙度設置為0.15 μm[5]。

圖10 -2.59°攻角下的轉捩位置示意圖Fig.10 Transition location on DLR-F4 with AoA of -2.59°

圖11 -0.87°攻角下的轉捩位置示意圖Fig.11 Transition location on DLR-F4 with AoA of -0.87°

圖10、圖11是不同攻角下DLR-F4風洞實驗和數值計算的轉捩位置對比。轉捩模型能夠較準確預測靠近翼根處的橫流不穩定性占主導的轉捩區域。圖11所示機翼中段部位，數值計算同實驗存在差距，現有模型預測的T-S波轉捩過早發生。

4 結 論

本文橫流轉捩模型不確定度量化分析與參數研究結論如下：

1) 參數調整對轉捩不確定度貢獻明顯。在參數cCF,h與cθt給定范圍后，轉捩區Cf不確定度較大，層流區為0。低速平板轉捩區Cf不確定度最大達90%，后掠翼轉捩區不確定度最大達189%。

2) 根據參數靈敏度指數分析結果，在橫流轉捩中，參數cCF對Cf和轉捩起始位置的影響要大于參數cθt的影響。應選取橫流參數cCF對模型進行標定。粗糙度h作為固有參數也會影響橫流轉捩，在風洞實驗與飛行試驗中應進行精密測量。

3) 以不確定度及敏感性分析結果為指導進行重新標定后的橫流模型對變粗糙度NFL- 0415翼型、帶傾角的6:1標準橢球體和DLR-F4翼身組合體的橫流轉捩能夠進行較好地預測。

基于參數不確定性的橫流轉捩模型不確定度與參數敏感性研究，能夠量化模型參數對轉捩的影響，提供轉捩結果誤差帶定量分布，具有工程指導價值。參數導致的模型不確定度和敏感性定量結論，對研究者進行模型使用、標定與修改具有參考價值。研究方法具有通用性，可用于各類轉捩/湍流模型的不確定度分析，甄別模型的關鍵參數，指導模型的精細化調試，對模型的改進與工程應用有所裨益。