基于隨機-模糊法的巖體風化分帶

楊國俊

(中國鐵路設計集團有限公司，天津 300251)

1 概述

鐵路工程地質(zhì)勘察項目一般具有涉及線路長、跨越區(qū)域廣、巖性復雜且種類多等特點。巖體的風化程度對路基、橋、隧道等工程基礎的設計至關重要，對項目的投資也有巨大影響。因此，合理劃分巖體風化帶對鐵路工程地質(zhì)勘察具有十分重要的意義[1]。

國內(nèi)外關于巖體風化分帶的研究可分為定性和定量2個方面。定性劃分依據(jù)主要有孔德坊提出的巖體風化帶7種區(qū)分標志[2]，以及GB50021—2001(2009版)《巖土工程勘察規(guī)范》、GB50487—2008《水利水電工程地質(zhì)勘察規(guī)范》中關于風化分帶的規(guī)定[3-4]，此類方法主要基于野外地質(zhì)調(diào)查，從巖體顏色改變、強度降低、次生礦物蝕變、節(jié)理變化、機械破碎情況、錘擊聲音等方面對風化程度進行分級。然而，這種定性劃分方法隨意性較強，很難有一個準確客觀的劃分界線。

隨著對巖石風化分帶研究的加深，逐漸發(fā)展出風化程度系數(shù)、裂縫系數(shù)和堅固度、風化系數(shù)、巖石質(zhì)量指標RQD及點荷載強度指數(shù)等用于評價巖體風化程度[5]。但由于巖體的復雜性，很難有一種指標可以綜合反映巖體因風化影響而發(fā)生的各類地質(zhì)特征變化。一些學者針對該問題進行了相關研究， 熊文林等發(fā)現(xiàn)，巖體樣本值既存在隨機不確定性，又存在模糊不確定性。傳統(tǒng)的統(tǒng)計方法只適用于處理巖樣選取時的隨機不確定性，未能考慮巖體類別劃分時的模糊性，故提出采用隨機-模糊處理方法對邊坡工程中巖石力學參數(shù)進行分析[6-7]。以下通過運用隨機-模糊方法中模糊隸屬度的計算方法和上述所提到的“波速比”量化指標，建立一種新的巖體風化分帶方法，并將該方法應用某巖質(zhì)邊坡的風化分帶中，為類似工程提供借鑒。

2 基于隨機-模糊法的風化分帶

2.1 技術流程

相較于其他特征指標，縱波波速能夠比較全面地反映巖體特征(如巖體密度、完整性、碎裂程度等)因風化影響而產(chǎn)生的變化，故風化巖體聲波波速與新鮮巖體聲波波速之比可以比較全面地反應風化巖體的風化程度。以TB10077—2018《鐵路工程巖土分類標準》中基于波速比對風化分帶進行定量劃分為基礎，結合隨機-模糊統(tǒng)計方法對風化帶邊界進行修正，技術流程如圖1所示。

2.2 風化帶初步定量劃分

巖體的波速特征反映了巖體的密度、巖體結構、裂隙發(fā)育程度等，一般情況下，隨著巖體的結構松散、破碎程度增加，聲波表現(xiàn)為波速、振幅減小和主頻向低端移動等規(guī)律[8-9]。

GB/T50218—2014《工程巖體分級標準》規(guī)定，巖體完整性系數(shù)KV的計算公式為

(1)

其中，KV為完整性系數(shù)；Vmp為巖體實測縱波速度；Vrp為測區(qū)完整、新鮮巖塊的縱波速度。選取波速比來定量劃分邊坡巖體的風化帶，不僅指標易得，而且能充分反映風化作用對巖體密度、巖體結構等影響程度，克服了其他指標只能反映單一風化特征的缺陷[10]。

根據(jù)TB10077—2019《鐵路工程巖土分類標準》中一般巖體質(zhì)量分類方法，通過地震折射或震源車等在鐵路沿線進行聲波測試，將每個墩臺位置及其它需探明巖層位置處設置為1個虛擬孔，測出虛擬孔各個深度的巖體縱波波速Vp(沿豎直方向每1 m測1次；若需更高精度，則測點間距可縮小)，然后計算出各虛擬孔處各深度位置風化巖體與新鮮巖體的縱波波速比。

巖體中若出現(xiàn)斷層、斷裂等控制性結構時，波速比會發(fā)生突變，需另行考慮其風化程度。一般情況下，在無控制性結構時，巖層埋深越大，巖體的風化程度就越小，波速比隨之增大。由于地下水及斷裂等特殊構造的存在，以及波速測試所產(chǎn)生的誤差，波速比可能波動比較大，對風化帶的劃分帶來較大不便。以下采用最小二乘法對所得的原始數(shù)據(jù)進行擬合，得到波速比沿孔深分布曲線，再通過該擬合曲線(各深度波速比自擬合曲線讀出)以及規(guī)范中波速比與風化帶對應關系進行風化帶的初步劃分。

2.3 隨機-模糊法的應用

在進行基于波速比的風化分帶定量劃分時，垂直地面方向上每1 m讀一次波速，這樣進行波速測試顯然具有隨機不確定性。另外，由于巖體力學性質(zhì)受多種因素控制，其數(shù)據(jù)在空間上有較大的變異性，風化帶邊界難以確定，從而使其劃分具有模糊不確定性。傳統(tǒng)的統(tǒng)計學方法僅能處理隨機不確定性，但忽略了模糊不確定性[11-13]。綜合考慮隨機不確定性和模糊不確定性，引入隨機-模糊方法進行參數(shù)分析。

(1)模糊均值

若通過定義式進行模糊均值的求解，則必須事先得到巖體物理力學參數(shù)的隸屬函數(shù)和概率密度函數(shù)，但實際應用中，獲得力學參數(shù)的概率密度函數(shù)是一個十分復雜的過程，必須在假定力學參數(shù)概率分布的前提下進行巖體參數(shù)概率密度函數(shù)的求取，故需要從其它角度推導模糊不確性的簡化公式。

(2)

(3)

則式(3)就是所求力學性質(zhì)參數(shù)的特征均值，根據(jù)所論問題的性質(zhì)，可用如下的隸屬函數(shù)表示

(4)

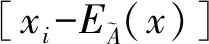
(5)

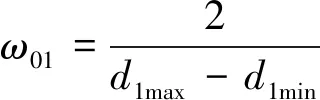
(6)

按照實測數(shù)據(jù)整體上隸屬于樣本模糊子集的程度應為最大的原則，依此組成目標函數(shù)

(7)

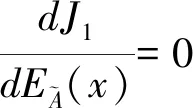
(8)

式(8)為巖體樣本物理力學參數(shù)模糊均值的計算公式，它是隱函數(shù)形式，需迭代求解。

(2)迭代方法

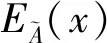
2.4 風化帶邊界位置修正

TB10077—2019《鐵路工程巖土分類標準》中，依據(jù)風化巖體與新鮮巖體聲波縱波波速比對巖體進行風化帶劃分的方法為經(jīng)驗法，能夠在一定的范圍內(nèi)劃定風化帶。然而，由于風化帶與波速比的對應關系是通過工程經(jīng)驗得到的，風化帶邊界位置的確定非常模糊。

可根據(jù)2.3中的計算方法，運用各風化帶波速比的模糊均值分別計算出風化帶邊界附近各點處巖體波速比對于相鄰2個風化帶的模糊隸屬度。根據(jù)隸屬度最大原則，某點屬于哪個風化帶取決于它相對于相鄰的2個風化帶哪個的模糊隸屬度大。

3 工程實例

研究區(qū)域巖性單一，主要以太古代晚期混合花崗巖為主，無特殊構造。影響巖體物理力學性質(zhì)的主要因素是降雨、氣候、大氣溫差等，導致產(chǎn)生具有不同物理力學性質(zhì)的風化帶巖體。

采用震源車測出每個點位置巖體縱波波速，按照上述方法對該橋梁工程地基進行風化帶劃分。

3.1 初步劃分風化帶

依據(jù)巖體聲波波速比對虛擬孔位置巖體進行風化帶初步劃分，以18-WT-1號虛擬孔為例，經(jīng)測試，該孔中新鮮巖體縱波波速為5 500 m/s。圖2中數(shù)據(jù)為風化巖體縱波波速與新鮮巖縱波波速之比(每隔1 m統(tǒng)計一次)，再采用最小二乘法進行擬合，得到擬合曲線，并運用優(yōu)化結果進行風化帶劃分，初步劃分結果見表1。

圖2 波速比數(shù)據(jù)擬合

表1 18-WT-1號虛擬孔巖體風化帶初步劃分結果 m

3.2 風化帶邊界修正

表2為修正后18-WT-1號虛擬孔強風化帶與弱風化帶界線附近巖體的波速比(根據(jù)擬合公式得到)。

表2 風化帶邊界附近巖體波速比

在確定各風化帶巖體波速比模糊均值的過程中，同時能夠得出各樣本巖體波速比對所劃定模糊集的隸屬度。因此，可以運用最大隸屬度原則對某位置處的巖體是否屬于某風化帶進行定量分析，具體做法如下。

①運用迭代方法求出兩風化帶波速比的模糊均值。經(jīng)計算，弱風化帶巖體波速比模糊均值為0.737 4；強風化巖體波速比模糊均值為0.551 6。

②將模糊均值代入式(3)，分別計算各波速比對于強風化帶和弱風化帶的模糊隸屬度，計算結果見表3。

由表3可知，孔深19 m時，測點對弱風化帶的模糊隸屬度首次大于其相對于強風化帶的模糊隸屬度，說明孔深19 m處為弱風化帶巖體，分界線應處于18 m與19 m之間(取18.5 m)；另外，孔深17～20 m之間的巖體模糊隸屬度均較小，也符合過渡帶的性質(zhì)。

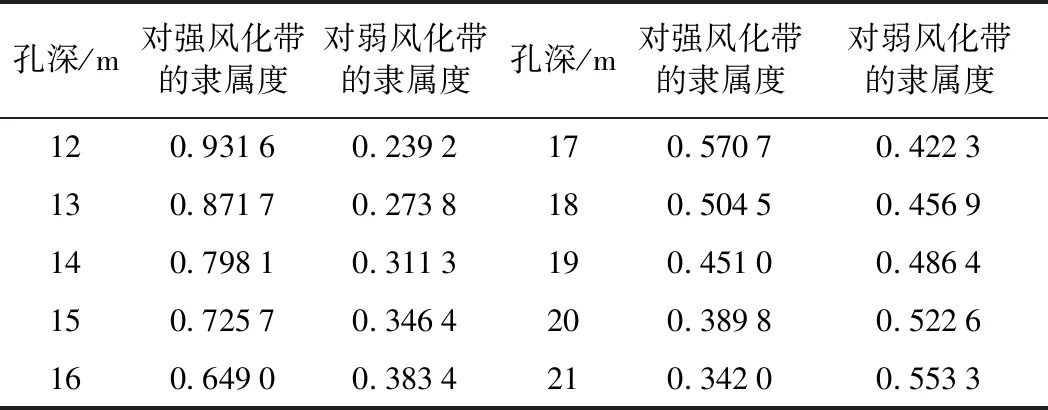
表3 測點對不同風化帶的模糊隸屬度

3.3 鉆探驗證

現(xiàn)場巖芯照片如圖3所示，受人為認識程度的影響，現(xiàn)場人員判定強、弱風化分界線在19.5 m處，但根據(jù)塊徑、新鮮程度判斷，將分界線定位18.5 m更為合理，因而新方法準確性較高。

圖3 18-ZD-01孔巖芯照片(15～20 m)

運用同樣的做法分別對18-WT-1虛擬孔的其他風化帶邊界進行修正，結果見表4。

表4 18-WT-1號孔風化分帶結果 m

由表4可知，新方法能夠比較精確地判斷風化帶邊界，克服了傳統(tǒng)方法[14]在風化帶邊界確定中的不確定性，而傳統(tǒng)方法進行風化分帶時會不可避免地出現(xiàn)兩風化帶重疊[15-16]，造成其風化界線難以確定。

4 結論

(1)基于隨機-模糊法的巖體風化分帶方法具有成本低、速度快、效率高、易于實現(xiàn)等優(yōu)勢。

(2)巖體縱波波速與巖體完整性、碎裂程度、巖體密度等密切相關，波速比能夠充分體現(xiàn)巖體的風化程度，故新方法適用于類似于巖性單一、水文條件簡單的巖質(zhì)邊坡巖體。

(3)通過模糊隸屬度對風化帶邊界進行修正，改變了以往只能靠經(jīng)驗進行風化帶劃分的弊端，使得風化帶劃分結果更為準確。