基于四元數的醫用機器人定位準確度評價

王浩，孟祥峰，王權，張超，王晨希，李佳戈

中國食品藥品檢定研究院 光機電室，北京 100050

引言

近年來，在人工智能、自動控制與傳感器技術的推動下，醫用機器人領域發展很快，面向骨科、神經外科、心血管等臨床需求，科研成果不斷涌現[1-5]，國產創新產品也在陸續上市[6]。根據國外醫用機器人應用情況和監管機構的反饋[7]，醫用機器人的安全性、有效性研究還有待深入，臨床風險依然存在，產品質量評價、上市前、上市后監管缺乏專用的標準體系，急需研究和完善。從標準化的角度看，國際電工聯合會、國際標準化組織等都在積極推進標準化研究。在電氣安全方面，康復機器人[8]、手術機器人[9]等國際標準已經發布，從醫用電氣設備的電氣安全角度指導質量評價。在風險管理方面，醫療器械自治能力[10]國際標準也已經發布，提出了自治能力分級的理念，有助于開展醫用機器人的風險管理活動。

在性能方面，醫用機器人缺乏專用標準，關鍵指標與評價方法尚未建立，部分沿用工業機器人的評價思路[11]，對醫療器械的特殊性考量有待加強[12-13]，方法也需要完善。其中，定位準確度是描述機械臂精準操作器械能力的重要指標之一，目前業內缺乏統一的評價方法，影響產品檢驗結果的可比性與可溯源性，阻礙產品上市與后續監管。根據數學原理，如何建立機器人坐標系（產品）與測量工具（檢驗設備）坐標系之間的轉換關系，是評價醫用機器人定位準確度的核心問題，不同的機器人標準給出的方法差別較大，例如GB/T 12642-2013[11]使用立方體或長方體作為體模，選擇對角面上的五個點為靶點計算定位準確度，而ASTM F2554-2010[14]使用特殊形狀的凹槽體模（預先標記47 個點），選取至少6 個靶點計算定位準確度。上述標準均未描述具體的坐標系轉換方法。

本文在實驗室條件下使用具體產品和坐標系測量裝置進行實驗，使用四元數法[15]對坐標系轉換結果進行計算，分析坐標系轉換模型參數、靶點數量等因素對定位準確度的影響，目的是進一步明確醫用機器人定位準確度的測量方法，為下一步建立專用標準提供參考。

1 實驗材料與方法

1.1 實驗材料與實驗環境

待測樣品為外科導航式手術輔助機器人，機械臂有6 個自由度，可在邊長為1 m 的立方體區域內活動，用于手術器械的固定及方向導引。樣品自身的軟件組件可以實時記錄機械臂器械末端的位置，提供機器人坐標系的讀數。該樣品聲稱的定位準確度＜1 mm。實驗室測量設備為便攜式三維測量臂，可進行接觸式位置測量，驗收標準滿足ISO 10360-12:2016[16]標準，定位測量精度＜0.06 mm，測量范圍能夠充分覆蓋待測樣品的活動空間。實驗室環境為室內平地，溫度為22 室，相對濕度為36%，實驗期間保持穩定。待測設備和測量臂底座固定，未見明顯振動或位移。

1.2 坐標系轉換模型

機器人機械臂器械末端坐標系記為坐標系r，實驗室設備的測量工具頭坐標系記為坐標系l。實驗室設備和機器人分別記錄靶點坐標，記為rl和rr。實驗室設備的點坐標rl轉換到機器人坐標系下，得到預測點 ，那么預測點與機器人實測點rr之間的距離即定位準確度。

根據四元數法的思路，坐標系轉換可分解為三個步驟，即“平移—拉伸—旋轉”。假設靶點位置在機器人與測量臂測量時均保持不變，即軌跡內部各點的相對位置不變（符合剛體定義），且兩個坐標系都是直角坐標系，數學模型可以用公式(1)表示：

其中r0代表平移量，s代表比例因子（拉伸或壓縮的倍數），R為旋轉函數或旋轉矩陣。平移量實質上是兩個坐標系原點的距離。在坐標系轉換過程中，坐標系r和坐標系l 可以分別減去全體靶點的幾何中心坐標，使得兩個坐標系的原點重合，此時平移量為0，記平移后的坐標值分別為rl'、rr'。對剛性物體而言，比例因子理論上等于1，那么公式(1)變成了對旋轉矩陣的直接求解。利用坐標系轉換中的點積不變性，使用三組通過機器人坐標系rl原點的三個彼此正交的單位向量和工具坐標系l 對應的向量，分別與同一個靶點對應的向量求點積，可重建旋轉矩陣。

在實際測量與計算中，比例因子和旋轉矩陣的求解屬于優化問題，等同于尋找使預測點與實測點之間誤差最小的匹配關系。本次實驗中，總體誤差的表述如公式(2)所示，那么優化問題即求解erms的最小值。

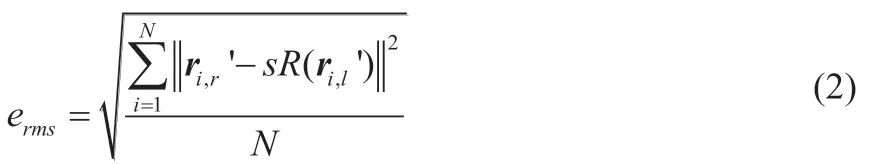
其中N為靶點個數，ri,r'、ri,l'分別為第i個靶點在平移后的機器人坐標系和工具坐標系下的值。為了使(2)達到最小值，參考江剛武等[15]的推導，比例因子與旋轉矩陣之間可構造如下關系，如公式(3)所示。

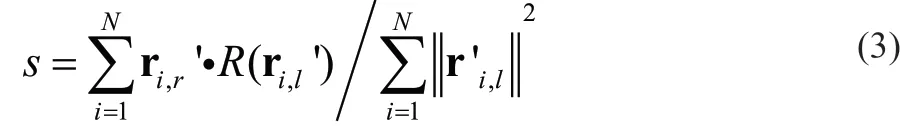
當旋轉矩陣確定之后，比例因子可通過公式(3)計算得到。

旋轉矩陣可以用單位四元數的形式表述。記四元數用于描述旋轉關系，其實部和虛部如公式(4)所示。

那么經過推導，旋轉矩陣可以表述為公式(5)。

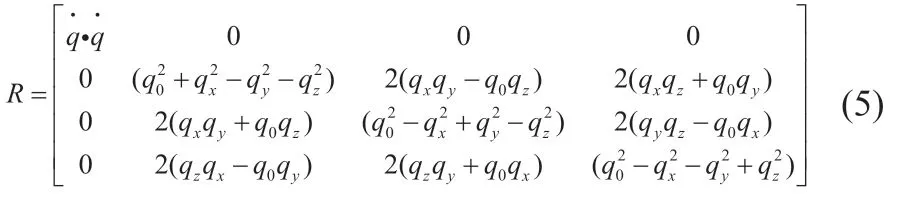
此時優化問題的關鍵是求解四元數本身。如果把四元數代入(2)，經過系列推導，最終得到是矩陣N 的最大特征值對應的特征向量，N 表述為公式(6)。

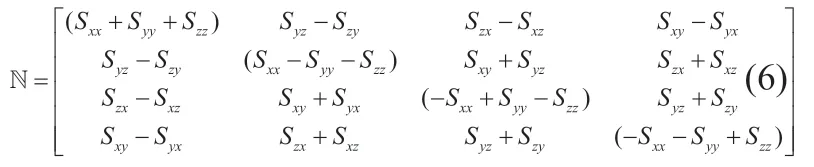
其中Sxx可表述為公式(7)，其他可以此類推。以上公式是坐標系轉換的依據。

1.3 操作流程

根據實際臨床應用，在有效工作空間范圍內選取40 個不同位置的靶點。在每個靶點位置，機器人坐標系和工具坐標系（接觸式測量）同步記錄坐標值。依托40 個靶點，進行坐標系轉換計算和定位準確度測量。為了分析靶點數量對定位準確度的影響，從40 個靶點中均勻隨機抽樣n個點（n從5 到40 遞增，步長為5），進行坐標系轉換和定位準確度測量，重復500 次，對抽樣批和全體靶點分別統計定位準確度的分布情況。

2 實驗結果

2.1 總體誤差

40 個靶點在機器人坐標系和實驗室工具坐標系下記錄的原始坐標數值如圖1 所示，其中藍色為實驗室工具坐標系記錄的坐標值，紅色為機器人坐標系記錄的坐標值。

使用1.2 中的各公式進行坐標系轉換，得到比例因子為0.999 7。圖2 所示為各點的定位準確度，最大值1.10 mm，最小值0.10 mm。根據公式(2)計算，得到總體誤差為0.59 mm。

可以看出，實際計算得到的比例因子與1 非常接近，剛體假設近似成立。為了進一步評估比例因子對坐標系轉換模型的影響，把比例因子替換為1，重新進行計算，得到各點的定位準確度。圖3 所示為結果的對比，紅色圓圈為比例因子0.999 7 對應結果，藍色倒三角為比例因子1 對應結果，可見分布趨勢相似，但數值變化比較明顯。總體誤差由0.59 mm 變為0.54 mm，幅度為7.74%。

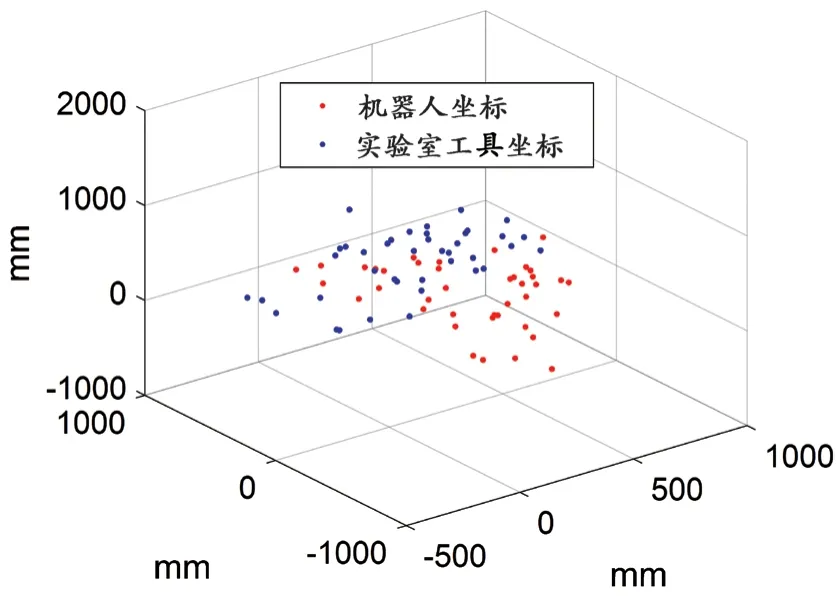
圖1 靶點的原始坐標數值

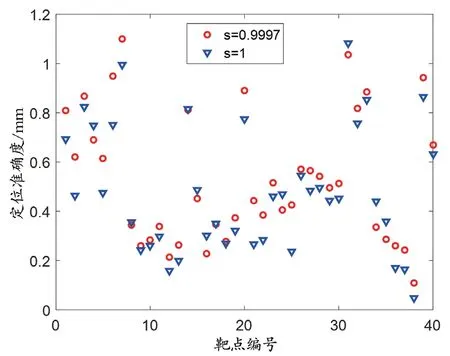
圖2 各點的定位準確度

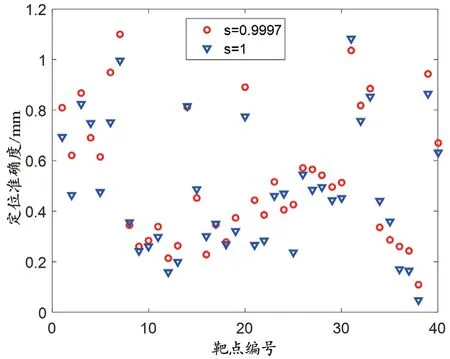
圖3 根據不同比例因子計算的定位準確度

2.2 靶點抽樣

從40 個靶點中隨機抽取的n個靶點（n從5 逐步增加到40，步長為5，每一步抽樣500 次）進行坐標系轉換，抽樣批的總體誤差分布與抽樣批樣品數量的關系如圖4 的箱式圖[17]所示，紅色橫線代表每個樣本量對應的總體誤差中位數，藍色矩形的上下限代表兩個四分限，黑色橫線分別代表非異常范圍的上下限，紅色+號代表極端異常值。根據圖4，抽樣數量越小，方差越大，極端異常值也越多，說明抽樣數量對坐標系轉換模型和總體誤差都有顯著影響。

圖4 抽樣批的總體誤差箱式圖

為了進一步觀察抽樣數量對坐標系轉換模型的影響，基于抽樣批構建坐標系轉換模型后計算全部40 個靶點的總體誤差，繪制箱式圖，結果如圖5 所示。其趨勢與圖4 相似，抽樣點數越多，方差越小，表明實驗的精密度越高。

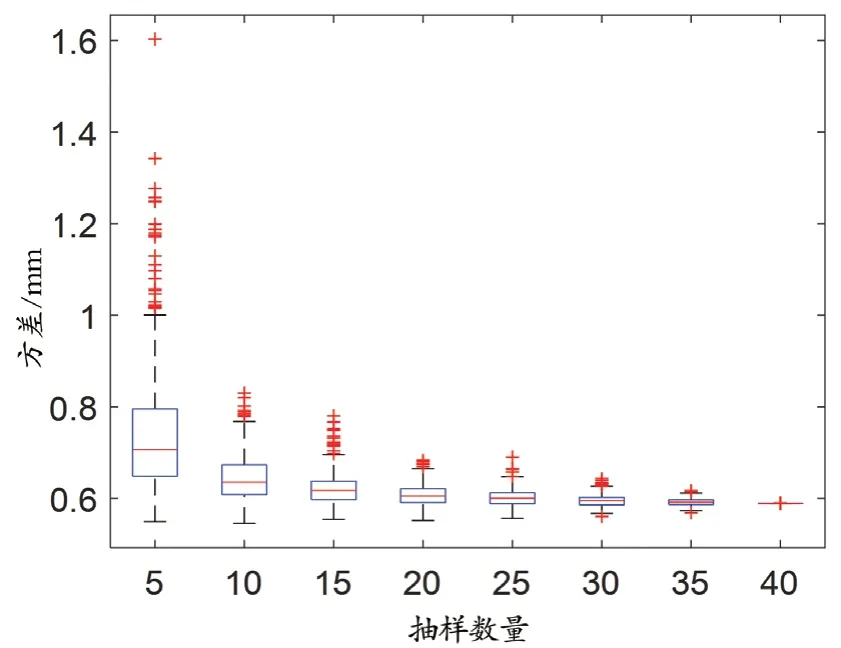
圖5 全部靶點的總體誤差箱式圖

3 討論

本次實驗對醫用機器人樣品進行了坐標測量，采用四元數模型開展了坐標系轉換計算，比較了不同因素對定位準確度結果的影響，發現以下問題在醫用機器人的質量評價中需要引起關注。

3.1 四元數模型參數

本次實驗中，氣候與機械環境平穩，實驗室測量設備自身的精度小于待測樣品10 倍以上（測量臂精度<0.02 mm，待測樣品聲稱精度<1 mm），測試條件總體良好。在此情形下，比例因子s 的實測值為0.999 7，與剛體的理論值1非常接近，但這兩種取值對應計算得到的定位準確度結果卻有明顯差別（0.05 mm，7.74%）。這說明坐標系轉換模型對比例因子的數值比較敏感，或者說梯度較大，意味著對實驗條件的要求比較嚴格，應避免引入額外的機械擾動、環境變化、坐標測量誤差等干擾因素。從標準化的角度看，這些因素在醫用機器人的定位準確度測量標準中需要予以明確規定，幫助保障不同的檢驗實驗室滿足測量結果的一致性和可靠性。

3.2 抽樣數量

為評估靶點數量對坐標系轉換模型的影響，本次實驗選取了不同的抽樣數量，分析了抽樣批的總體誤差和全體靶點的總體誤差，結果均說明抽樣數量越大，測量結果方差越小，精密度越好。本次實驗總共設置了40 個靶點，當采樣點數多于30 時，圖4 的箱式圖非異常范圍的上下限之差可收斂到0.2 mm 以下，而圖5 的箱式圖非異常范圍的上下限之差可收斂到0.1 mm 以下，說明用于建立坐標系轉換模型的靶點數量、用于驗證定位準確度的靶點數量均應設置合理的下限值。由于醫用機器人在臨床使用中的運動軌跡往往不規則且充滿變化，相對工業機器人而言更加復雜，意味著現有工業機器人標準的靶點抽樣數量（5 或6）可能難以滿足醫用機器人定位準確度評價的需要。醫用機器人的定位準確度評價有必要結合臨床使用場景，在以后的測試和研究中深入展開，加強與其他機器人標準的比較。。

本次實驗設計還存在一些不足之處。靶點選取范圍基本覆蓋了樣品的活動范圍，但靶點的抽樣僅采用了隨機抽取的方式，未對靶點組成的空間形狀提出進一步的設計，還不能支持體模的研制。下一步的研究有必要對靶點的選取方法開展更深入的評估，包括數量、空間形狀要求和距離，使得定位準確度的評價方法更加科學嚴謹，更接近標準化的需求。

4 結論

本文依據四元數理論，把坐標系轉換模型應用于醫用機器人的定位準確度評價問題，依托三維測量臂和具體樣品開展了實驗與仿真分析。結果說明坐標系轉換模型的比例因子、靶點數量等因素對實驗結果有明顯影響，對于醫用機器人專用性能標準的后續研究提供了有益的參考。