注氣式POGO 抑制系統模型研究

王 楠，容 易，胡久輝，張青松，秦旭東

（北京宇航系統工程研究所，北京，100076）

0 引 言

POGO 是液體運載火箭結構與其動力系統相互耦合而產生的縱向自激低頻振動[1,2]，會使運載火箭的振動環境惡化，可能造成箭上敏感元件及儀器設備受損或結構超限，對于載人航天，還會使宇航員出現身體不適，甚至危害宇航員的生命安全。因此，POGO 抑制是影響火箭飛行可靠性甚至飛行成敗的一項重大關鍵技術。

為抑制POGO 振動，通常在推進劑輸送管路系統上安裝蓄壓器，改變動力系統固有頻率特性，以此削弱和消除箭體結構與動力系統之間的耦合。中國現役長征系列液體運載火箭均使用了貯氣式POGO 抑制技術，抑制裝置為貯氣式蓄壓器[3～8]，而國外運載火箭則廣泛使用了注氣式POGO 抑制技術，核心裝置為注氣式蓄壓器[9～13]。隨著中國運載火箭技術的發展，POGO抑制系統裝置從貯氣式向注氣式的跨代升級已是大勢所趨。相比于貯氣式蓄壓器，注氣式蓄壓器具有如下特點：

a）能量值PV[6]可隨蓄壓器入口壓力實時連續調節，對動力系統的調頻能力更強；

b）蓄壓器氣枕為開式系統，工作過程中不斷有氣體的注入和排出，同時氣枕與液體推進劑之間還存在質量交換；

c）蓄壓器內氣液界面的穩定性受注氣和排氣的控制，排氣阻力過大時，氣體可能涌入輸送管內。

上述特點導致了注氣式蓄壓器動特性模型有別于金屬膜盒式蓄壓器，文獻[14]開展航天飛機POGO 抑制設計時，未考慮注氣和排氣可能帶來的影響。Ares I火箭POGO 抑制設計繼承了航天飛機、德爾塔運載火箭的經驗，蓄壓器選型過程中詳細討論了充氣過程中液位的變化規律[15]；萬屹侖等[16]也對注氣式蓄壓器工作特性及動特性模型進行了討論，認為氣枕成分單一，沒有深入討論影響蓄壓器動特性的因素。

本文建立了注氣式POGO 抑制系統線性化動特性模型，分析對比注氣式蓄壓器與貯氣式蓄壓器性能的差異，并通過試驗對動特性模型的正確性進行了驗證。

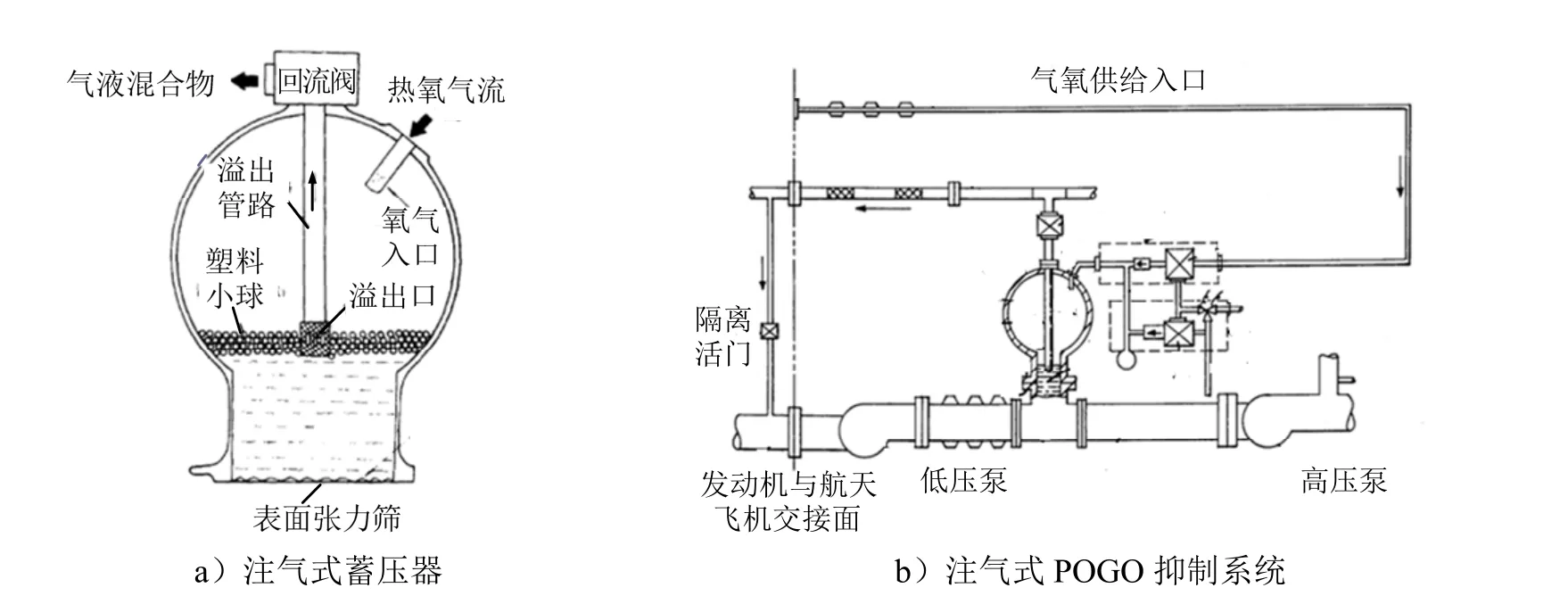
圖1 航天飛機注氣式POGO 抑制系統Fig.1 Gas-injected POGO Suppression System of Space Shuttle

1 線性化控制模型

注氣式POGO 抑制系統的核心是注氣式蓄壓器，蓄壓器氣枕為輸送系統提供一個集中柔性環節，是決定注氣式蓄壓器POGO 抑制能力的關鍵，由于注氣式蓄壓器的氣枕屬于開式系統，在建模方法上與貯氣式蓄壓器有較大的不同。

圖2 為一種注氣式蓄壓器的結構原理圖，蓄壓器設置有注氣管路和排氣管路，排氣管路限制了液位高度，當液位較低時，氣體從排氣管排出，當液位升高時，液體也可以從管路排出。蓄壓器氣枕和液位在注氣和排氣的共同作用下維持穩定。

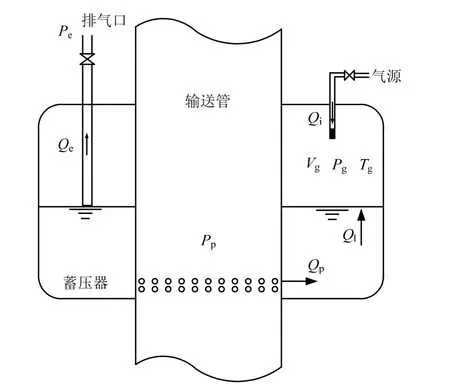
圖2 注氣式蓄壓器示意Fig.2 Diagrammatic Sketch of Gas-injected Accumulator

為簡化起見，不考慮氣枕與推進劑之間的質量交換（即不考慮推進劑蒸發量和氣體冷凝）。在脈動壓力作用下，氣枕的變化近似為等熵絕熱過程；排氣管始終保持和氣枕接觸，排氣管無液體排出，氣液界面做平移無大幅波動。對于氣枕內氣體有：

式中 Mg為氣枕內氣體總質量。

微分后有：

相比于氣體，液體的可壓縮性可以忽略不計，因此連通孔處的流量pQ 與氣液交界面處流量lQ 相等，即：

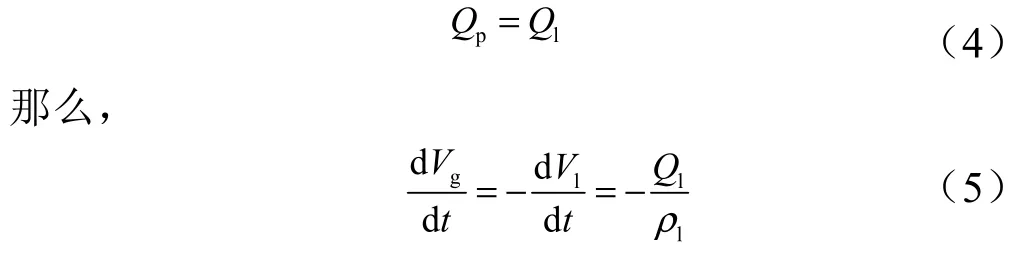
式中lρ 為液體密度。

為了便于描述，規定以輸送管內液體流向蓄壓器的方向為正，即以使得蓄壓器內氣枕體積減小的方向為正。

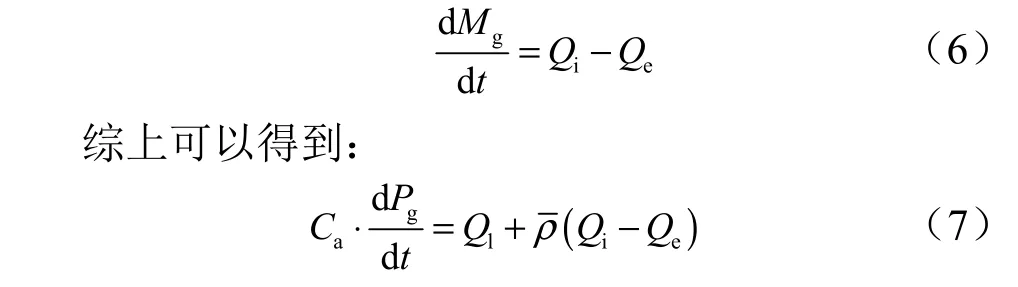
式中 δ 為脈動物理量。

按照不可壓流動方程有蓄壓器入口壓力pP 與氣枕壓力gP 的關系為[17]

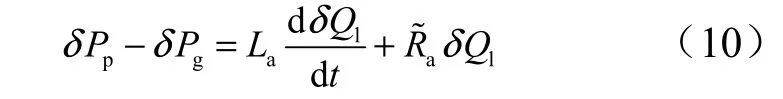
式中aL 為蓄壓器慣性；為蓄壓器阻尼系數。

注氣流量iQ 通常由供氣管路上孔板控制，設計狀態下孔板處于超臨界流動狀態，一般認為孔板流量不受下游擾動影響，因此 iQδ ≈0。

排氣流量eQ 由下式決定：

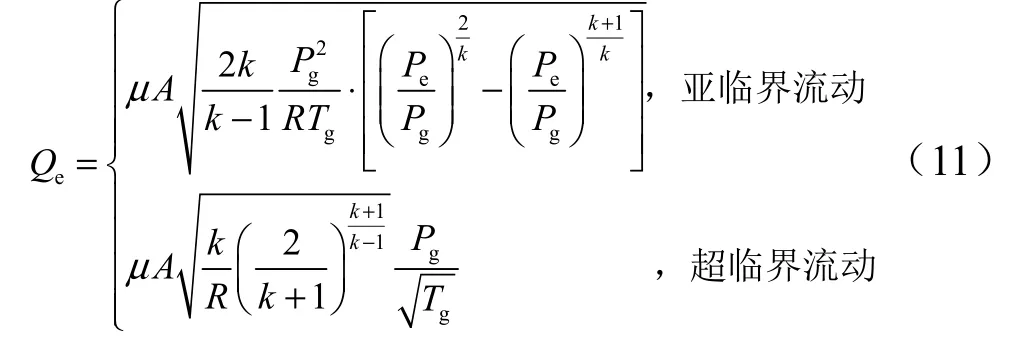
式中 μ 為孔板流量系數；A 為孔截面積；k 為氣體比熱比；R 為氣體常數。

對其進行小偏差線性化處理后可得如下形式的動態數學模型：

晌午，我到知青大院去還郝浮萍的自行車，她說，那個禿頭剛走，他是來道歉的，還留下二十塊錢，說是營養費。我說，既然傷得不重，就饒了他吧。郝浮萍面帶難色，說，田青青已經去了公社，這事恐怕蓋不住了。我知道禿頭來道歉并賠錢，這肯定是趙世奎的點子。一旦這事捅到上邊，必將引起一場軒然大波。

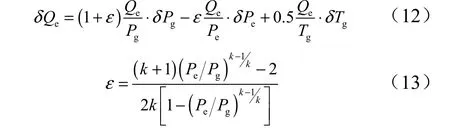
當處于超臨界流動時，ε=0。

對于本文研究的注氣式蓄壓器，氣體直接排至外界，背壓eP 即環境壓力（緩變量），認為δPe=0；根據試驗結果，蓄壓器內溫度主要受注入氣體溫度和流量控制，變化緩慢，因此 gTδ =0。

聯立上述各小偏差線性化等式，并做拉普拉斯變換，可以得到：

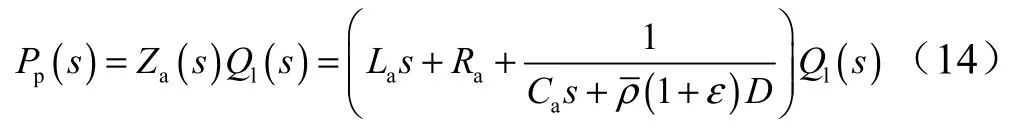
式中 D 為排氣管路穩態流量與氣枕壓力比值，D =Qe/ Pg； Za為注氣式蓄壓器阻抗。

貯氣式蓄壓器的動特性方程為

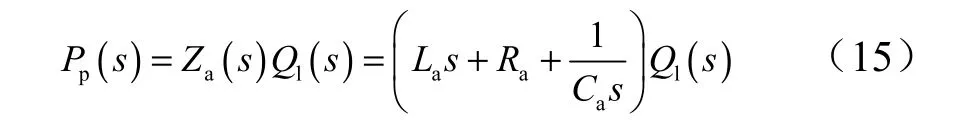
兩者的區別在于，排氣管路影響了注氣式蓄壓器動特性，本文稱1 +ε) D為排氣因子。

以某“水-氮氣”原理性注氣式蓄壓器為例，氣枕容積 Vg=50 L，穩態壓力 Pg=0.6 MPa，環境背壓Pe=0.1 MPa，排氣管路等效孔徑5 mm。排氣穩態流量Qe=0.0275 kg/s ， 系 數 D= 0.046 ×1 0?6m ? s2，1 +ε) D = 6.55 ×1 0?6m ? s2。 蓄 壓 器 柔 度Ca= 5.95 × 10?5m ? s2。

針對系統1 Hz 以上的激勵，蓄壓器柔度與排氣因子的相對效應為

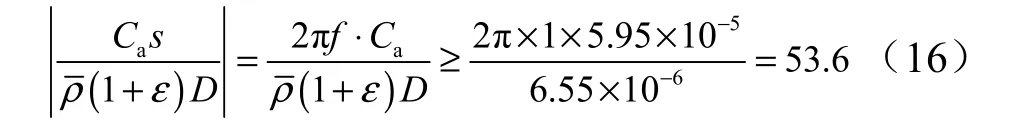
可以看出，在蓄壓器柔度較大的情況下，排氣管路對動特性的影響可忽略。注氣式蓄壓器的動特性方程形式與貯氣式蓄壓器一致。

2 兩種蓄壓器性能比對

影響蓄壓器性能的參數包括蓄壓器柔度、阻力和慣性等，相比于輸送管的慣性，純柔性蓄壓器的慣性是小量，蓄壓器阻力系數對系統動特性的影響很小，因此決定蓄壓器性能的參數主要為柔度。由上文討論可知，注氣式蓄壓器柔度如式（8）所示。

貯氣式蓄壓器的柔度可描述為

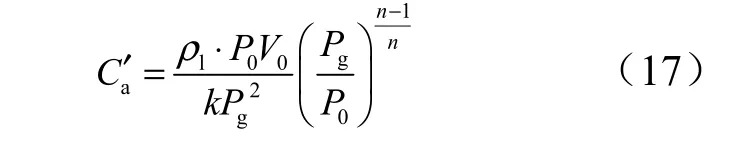
式中0P ，0V 分別為貯氣式蓄壓器初始氣枕壓力和初始氣枕容積；n 為貯氣式蓄壓器氣枕多變指數。

注氣式蓄壓器由于一般有限位管的作用，氣枕體積gV 恒定，可以看作是定體積過程；貯氣式蓄壓器的體積gV 隨入口壓力而變，為多變過程，蓄壓器入口變化不太迅速的情況下，可將其視為等溫過程，即n=1。

從柔度的表達式可以看出，注氣式蓄壓器的柔度與入口壓力成反比，貯氣式蓄壓器的柔度與入口壓力的平方成反比，運載火箭飛行過程中過載不斷增大，蓄壓器入口壓力一般隨之增大，因此注氣式蓄壓器柔度受入口壓力增大而衰減效應要明顯低于貯氣式蓄壓器，具有更強的POGO 抑制能力，這就使得注氣式蓄壓器系統容積可以做的更小。

圖3 為輸送系統包括輸送管路和末端的蓄壓器示意，輸送系統管路末端封堵，上游貯箱直徑遠大于輸送管路直徑，組成一個典型的“開-閉”系統，忽略管路阻力、蓄壓器慣性和阻力，可以得到系統的一階頻率為

式中dL 為輸送管的慣性， Ld=ld/ A，其中，dl 為輸送管線長度。

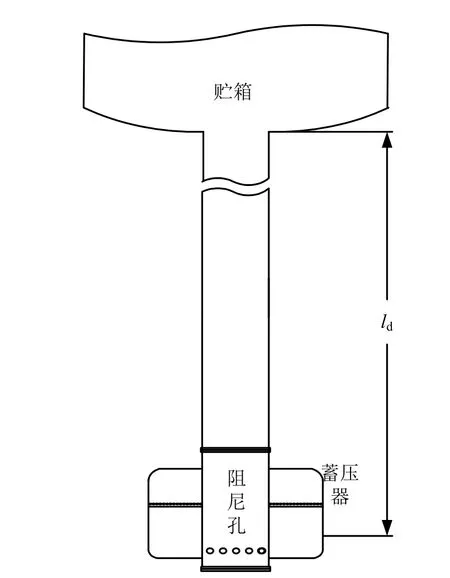
圖3 輸送管+蓄壓器系統示意Fig.3 Diagrammatic Sketch of a Pipe & Accumulator

對于相同的初始氣枕容積，兩種蓄壓器柔度隨著入口壓力變化如圖4 所示，其中，C0為蓄壓器入口壓力為P0時的柔度。可以看出，隨著入口壓力的升高，貯氣式蓄壓器柔度下降速率明顯快于注氣式蓄壓器，當飛行過程中蓄壓器入口壓力變化范圍較大時，貯氣式蓄壓器的柔度衰減很大，例如當壓力P=2P0時，貯氣式蓄壓器的柔度為0.25C0，而注氣式蓄壓器的柔度為0.5C0。

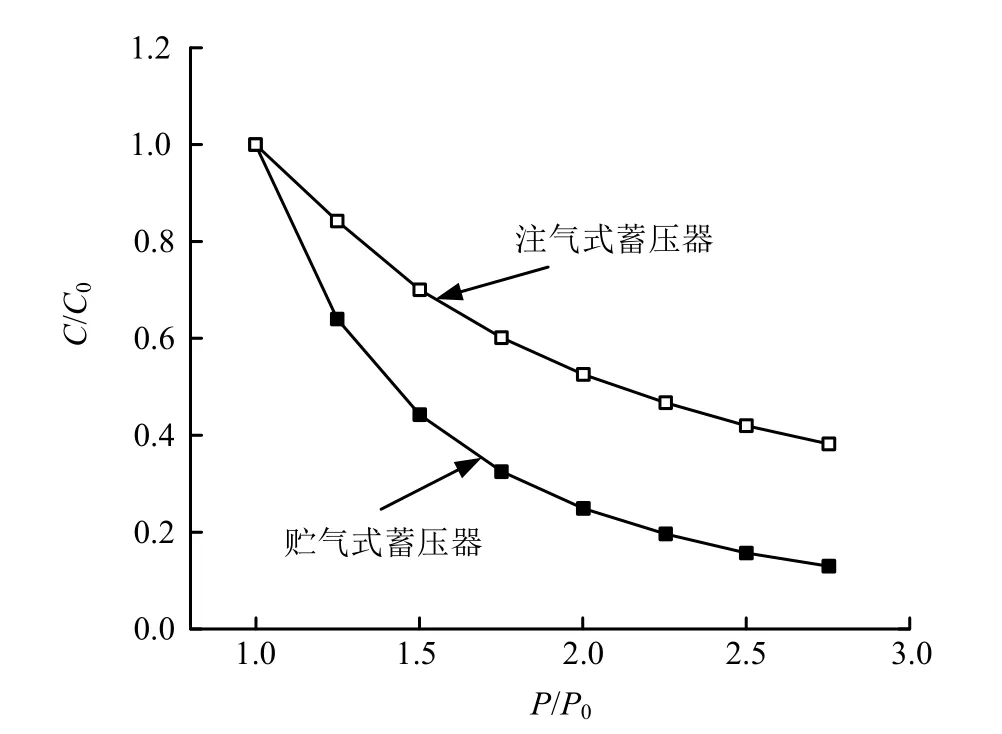
圖4 注氣式和貯氣式蓄壓器的柔度隨入口壓力變化Fig.4 Flexibility Variation with Inlet Pressure of Gas-injected and Gas-storaged Accumulator

隨著運載火箭規模的增大，輸送管路直徑增加（管路慣性減小），要將輸送系統頻率限制在一定范圍內，需要的蓄壓器柔度也越來越大。火箭動力系統一階頻率通常由泵前管路（見圖3）所決定，假定要將某一動力系統一階頻率降低至4 Hz 以下，兩種蓄壓器的氣枕容積隨著管徑增大的變化情況如圖5 所示，其中Vg0為輸送管直徑為D0時所需的蓄壓器氣枕容積。從圖中可以看出，當輸送管直徑達到4D0倍后，對貯氣式蓄壓器的氣腔容積需求已經達到D0直徑時的15 倍以上，約為注氣式蓄壓器體積的2 倍。

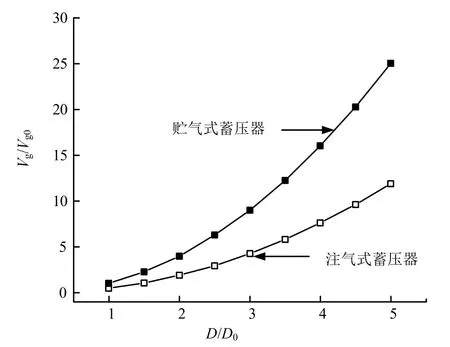
圖5 注氣式和貯氣式蓄壓器容積隨管路直徑變化Fig.5 Gas volume Variation with Pipe Diameter of Gas-injected and Gas-Storaged Accumulator

綜上所述，相同管路壓力條件下注氣式蓄壓器的變頻降幅能力越強；相同變頻需求下注氣式蓄壓器氣枕容積要求更小，結構效率更高。此外，注氣式蓄壓器相比于常見的金屬膜盒式蓄壓器（一種典型的貯氣式蓄壓器），沒有膜盒焊縫疲勞強度、膜盒穩定性等問題，工藝簡單可靠。

3 試驗驗證

為進一步驗證注氣式蓄壓器理論預示模型的正確性，利用安裝有注氣式POGO 抑制系統的輸送管進行了水介質動態特性試驗，試驗系統原理見圖6。注氣式蓄壓器由一套地面控制器控制注氣和排氣的時序，供氣系統提供恒定的壓力源，電磁閥控制氣源的通斷，由孔板限制流量，排氣管路通過電磁閥控制排氣流量。系統的脈動由安裝于管路底部的活塞式脈動壓力發生器生成，通過對管路沿程脈動壓力的測量，確定系統的動態特性。

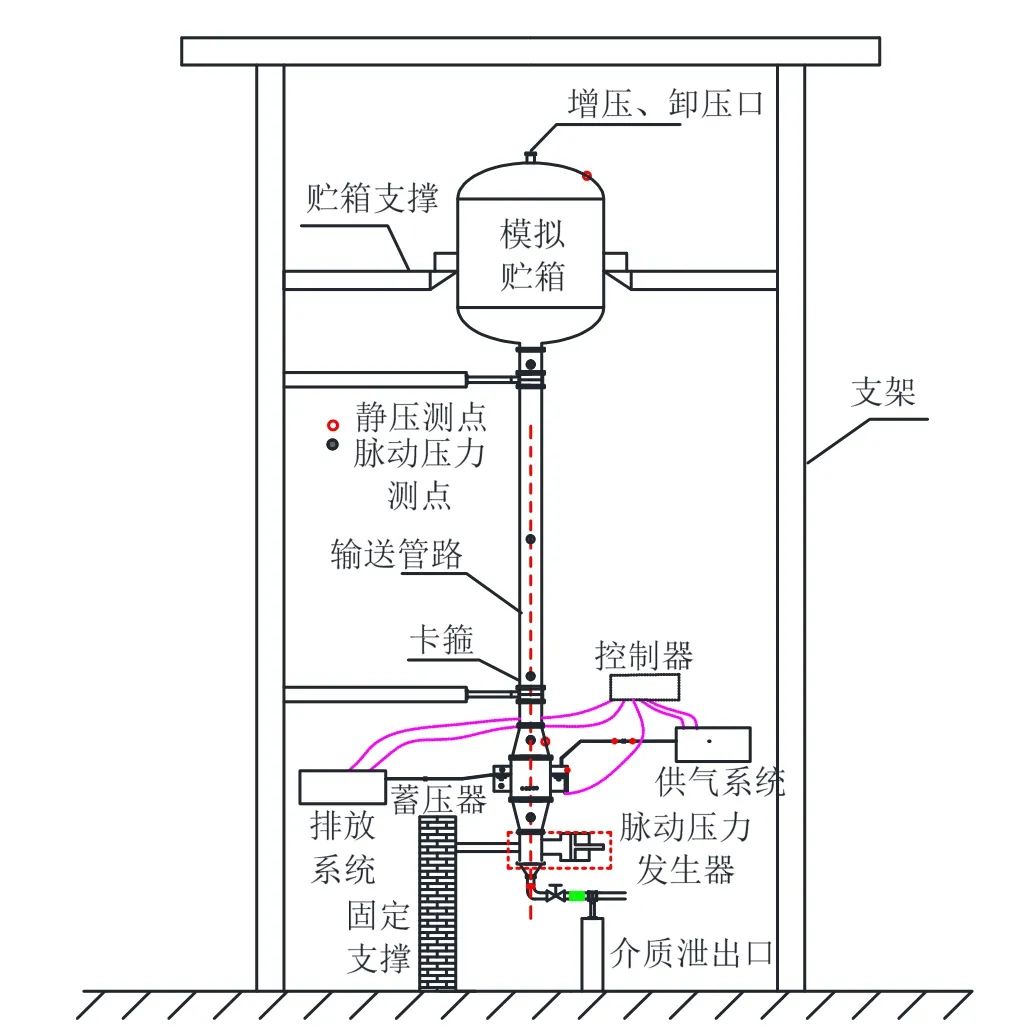
圖6 試驗系統原理Fig.6 Schematic Diagram of Test System

3.1 定壓掃頻激振

在保持蓄壓器入口壓力恒定的狀態下，激振系統做1.5～50 Hz 的掃頻激振，通過管路沿程脈動壓力傳感器的數據可得到管路系統一階頻率的試驗值，根據第1節的模型可計算出一階頻率的理論值，兩者對比如表1所示。由表1 可知，計算與試驗值的相對誤差在8%以內。

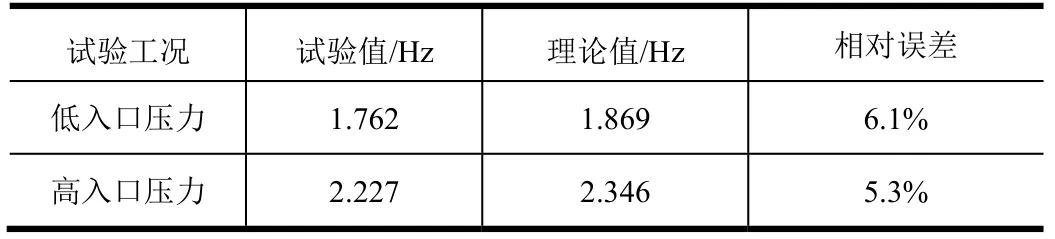
表1 定壓掃頻激振的試驗結果Tab.1 Test Result of Sweep Frequency Excitation with Const Pressure

3.2 飛行壓力隨機掃頻

注氣式蓄壓器模型推導中假定了泵入口穩態壓力變化過程不與管路內低頻脈動相耦合，即蓄壓器的動特性只與當前入口壓力有關，而與壓力變化速率無關。為了驗證該假設，通過貯箱增壓模擬一級飛行段注氣式蓄壓器入口壓力，通過控制加泄管路上截止閥的開閉或者貯箱放氣，模擬發動機啟動過程中和助推分離時刻，蓄壓器入口壓力突變的工況。脈動壓力發生器進行1.5～50 Hz 的寬帶隨機激振。

與注氣式蓄壓器的使用模式相對應，為防止發動機啟動負水擊使得蓄壓器內氣體涌入輸送管中，發動機起動前蓄壓器為無氣枕狀態，在發動機完成啟動后，將蓄壓器充氣至額定容積。圖7 為飛行狀態下動力系統一階頻率曲線。

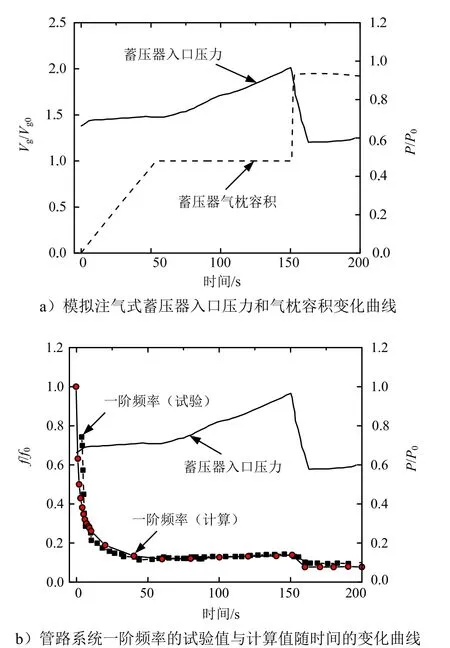
圖7 飛行狀態下動力系統一階頻率曲線Fig.7 First Order of Frequency of Power System in Flight

從圖7 中可以看出試驗數據與仿真數據的一致性良好；由于小氣枕容積狀態下缺少容積實測值，用理論氣枕容積預測的一階頻率與試驗值偏差相對較大。

4 結 論

本文對注氣式POGO 抑制動力學模型進行了推導和分析，分析了注氣式蓄壓器和貯氣式蓄壓器模型上的差異，理論分析指出排氣對注氣式蓄壓器動力學模型的影響，利用分析模型比較得出了注氣式POGO 抑制方式具有抑制能力高、對安裝空間要求低等優勢。通過輸送管路系統試驗驗證了注氣式蓄壓器線性化模型在不同壓力入口條件下的正確性。