基于APDL的擺線針輪傳動小周期動態嚙合仿真分析
孫曉超,張迎輝,盧琦,崔迪,何衛東
(1.遼寧加寶石化設備有限公司,遼寧 營口 115000;2.大連交通大學 機械工程學院,遼寧 大連 116028)*
RV(Rotate-Vector)減速器是由漸開線齒輪和行星擺線針輪組成的兩級減速傳動機構,具有傳動比大、體積小、剛度大、承載能力大、傳動精度和傳動效率高等優點,廣泛應用于工業機器人關節驅動裝置中[1-2].擺線針輪傳動副嚙合力的大小作為影響RV減速器傳動精度的重要因素,受到學者們的廣泛關注.張東生[3]等在變形協調原理的基礎上,提出了擺線針輪傳動動態受力分析理論,在全域內找到了最大接觸力和最大接觸應力,突破了傳統方法只能計算一個特殊位置的局限性.何衛東[4]應用赫茲理論,考慮到擺線輪修形引起初始間隙的影響后建立了各個接觸齒對受力與接觸變性的函數關系,準確計算出針輪同時受力齒數及大小.關天民[5]等應用解析法對修形后擺線輪和針齒嚙合時的初始間隙進行了準確計算,提出了完整的二差齒針擺傳動的有隙嚙合受力分析方法,更符合工程實際.鄭鈺馨[6]等在詳細闡述了無針齒套RV減速器擺線輪嚙合受力計算方法的基礎上,使用密切值法對多參數進行了嚙合力影響程度排序,確定了擺線輪厚度、曲柄軸偏心距以及針輪半徑為與受力密切相關的參數.姚燦江[7]利用 ANSYS Workbench進行RV減速器擺線輪系嚙合傳動過程的仿真分析,了解擺線輪系在嚙合過程中實際受力狀態,明確應力分布區域.梁帥鋒[8]等應用輪齒接觸分析(TCA)技術闡述了輪齒接觸分析計算過程中初始參考點求解的難點問題,求解出傳統修形方式下擺線針輪傳動的瞬時嚙合狀態、嚙合區域.以上分析均為假設擺線輪處于某一靜止狀態時的受力情況.李超群[9]等基于Adams虛擬樣機技術,發現經過正等距、正移距修形后,沿嚙合點法線方向會產生初始間隙,導致嚙合齒數減少,最大接觸力變大,該分析由于假設零件為絕對剛性,不能得到針擺嚙合的接觸應力.
本文以受力原理為基礎,結合有限元數值方法,求解出RV減速器擺線針輪傳動在曲柄軸轉動360°時各個擺線針輪嚙合齒對的有限元動態仿真受力結果,準確得到RV傳動一個小周期運動時的動態接觸應力變化規律,并與理論計算結果相比較,來驗證有限元模型的可靠性.
1 擺線針輪嚙合原理
1.1 內嚙合擺線針輪齒廓的形成
如圖1所示,以短幅外擺線MM′M″作為輪C的齒廓,M點作為輪B的齒廓,兩輪各繞其中心oc和oB作旋轉運動,就組成了即內嚙合擺線針輪傳動.在實際工程中,將M點轉化為半徑為rz的針齒,輪B為擺線輪.如果針輪固定不動,用一個轉臂連接擺線輪的中心oB來帶動擺線輪作公轉運動,則擺線輪就成為了行星輪,進而構成了擺線針輪行星傳動.
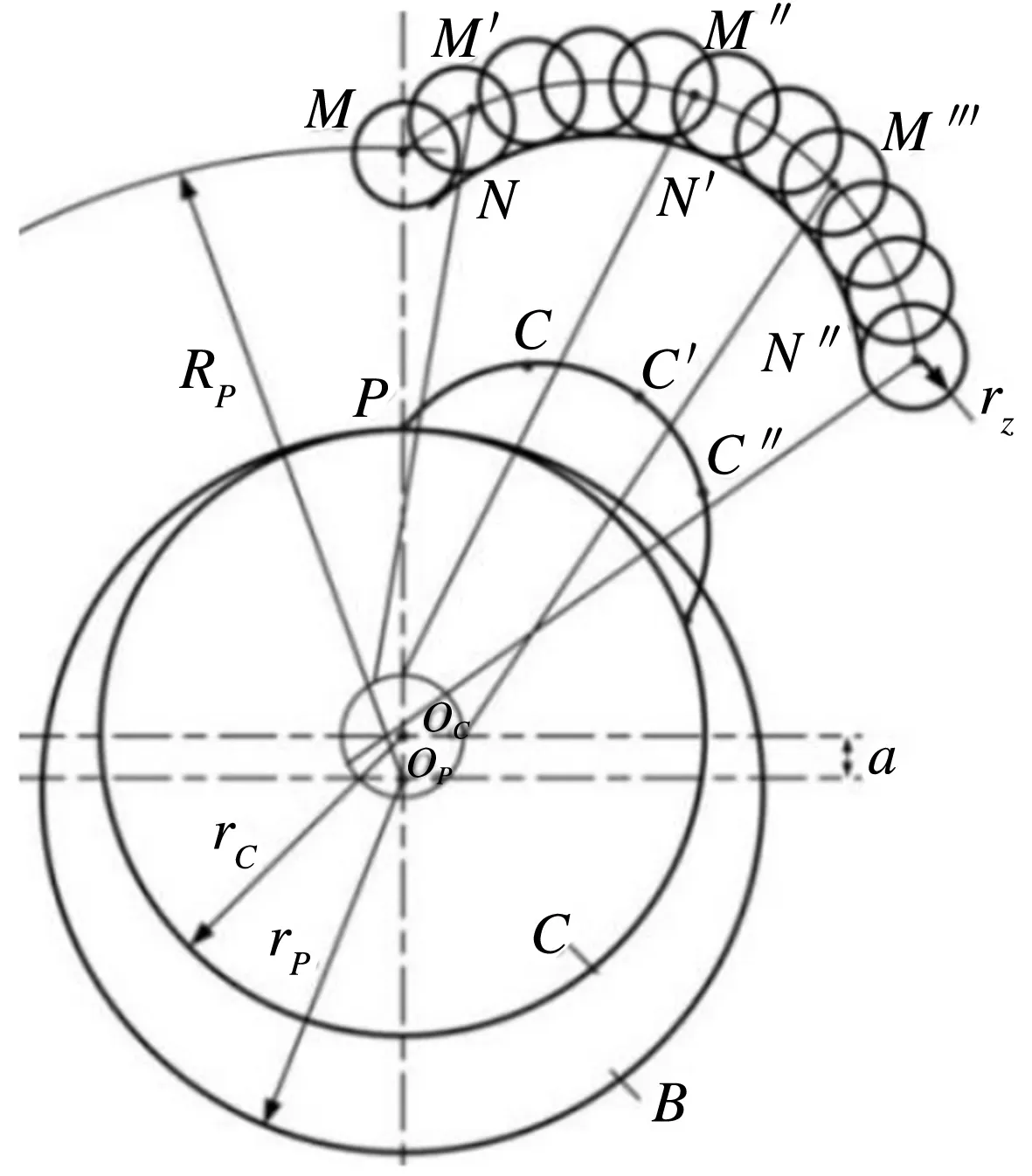
圖1 內嚙合擺線齒廓形成原理
1.2 擺線輪標準齒形方程式
針輪上的針齒為標準針齒,與之相嚙合而且沒有間隙的擺線齒形稱之為“標準理論齒形”.通過建立三個坐標系:固連于曲柄軸的坐標系XOpY、固連于針輪的坐標系XpOpYp、固連于擺線輪的坐標系XcOcYc、傳動比關系、幾何關系等,最終通過一系列的坐標變換,可以得到擺線輪在固連于擺線輪的坐標系XcOcYc中的標準齒形方程式[11].
(1)
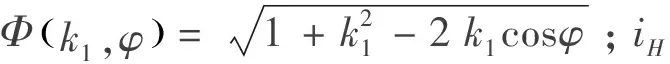
1.3 擺線輪修形齒形方程式
在擺線針輪傳動的實際應用過程中,如果按照標準齒形進行裝配或工作,會降低RV減速器的使用壽命.為了改善上述情況,實際的擺線輪齒廓不能采用標準齒形,而必須采用修正的擺線輪齒形[10-11].擺線輪的修形方法主要有三種,即移距修形法、等距修形法、轉角修形法[12].現階段關于擺線輪齒形的修形方法主要采用負等距與負移距相組合的修形方法,采用這種修形方法能保證輪齒嚙合所需要的間隙要求、并且保證一定的回差要求,取得了比較好的修形效果,得到了廣泛地應用.與上文所選的坐標系相同,仍在坐標系XcOcYc建立通用擺線輪齒形方程式,該方程式中包含了所有的修形方法,如下.
(2)
式中,a為偏心距;Zc為擺線輪的齒數;k1′為經過修形的擺線輪齒形短幅系數;Δrp為移距修形量;Δrrp為等距修形量;δ為轉角修形量.
RV40E減速器擺線針輪傳動幾何系數見表1.
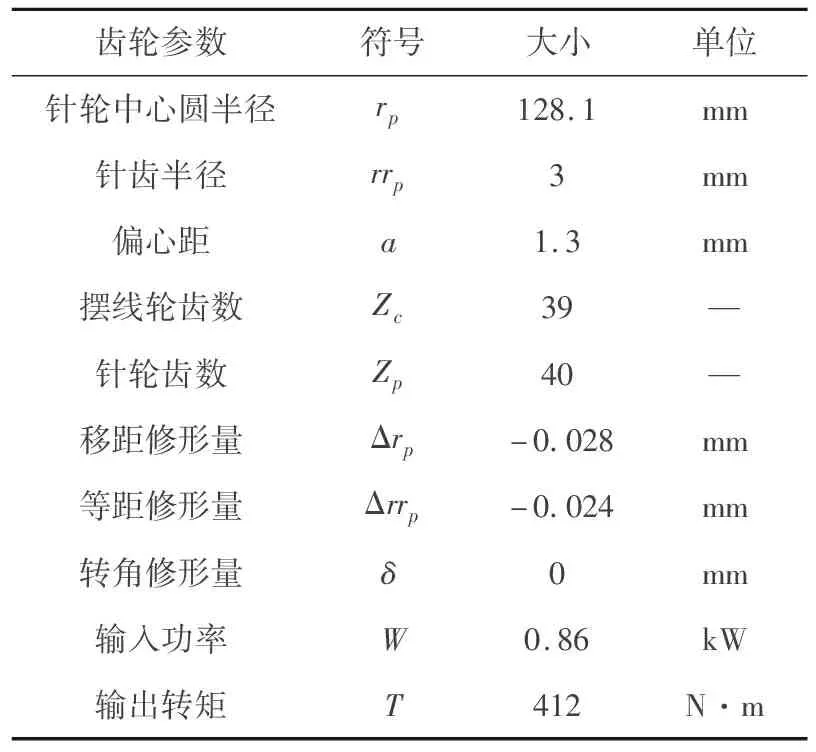
表1 RV40E減速器擺線針輪傳動幾何參數
2 有限元建模與邊界條件確定
2.1 有限元建模
在ANSYS中應用APDL參數化編程語言,生成擺線輪、針齒、軸承、曲柄軸、行星架等一系列零件,進行裝配.其中軸承采用ANSYS提供的約束單元類型MPC184,即包括一系列采用拉格朗日算法構建運動學約束的多節點單元,來模擬軸承的旋轉運動.在擺線輪軸承孔中心處生成單獨的節點,同時選取擺線輪軸承孔內表面節點,在軸承孔中心節點和軸承孔內表面節點之間自動生成多點約束方程,如圖2所示.
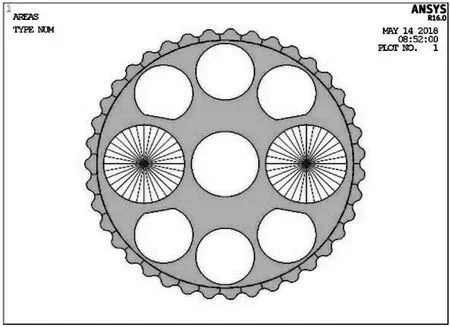
圖2 軸承孔多點約束方程
同理,在曲柄軸曲拐的中心處生成單獨的節點,同時選取曲拐外表面上的節點,在曲柄軸曲拐中心節點和曲拐外表面節點之間自動生成多點約束方程.最后,利用鉸鏈連接方法,在擺線輪軸承孔中心點和曲柄軸曲拐中心點之間沿z軸方向建立鉸鏈單元,如圖3所示.
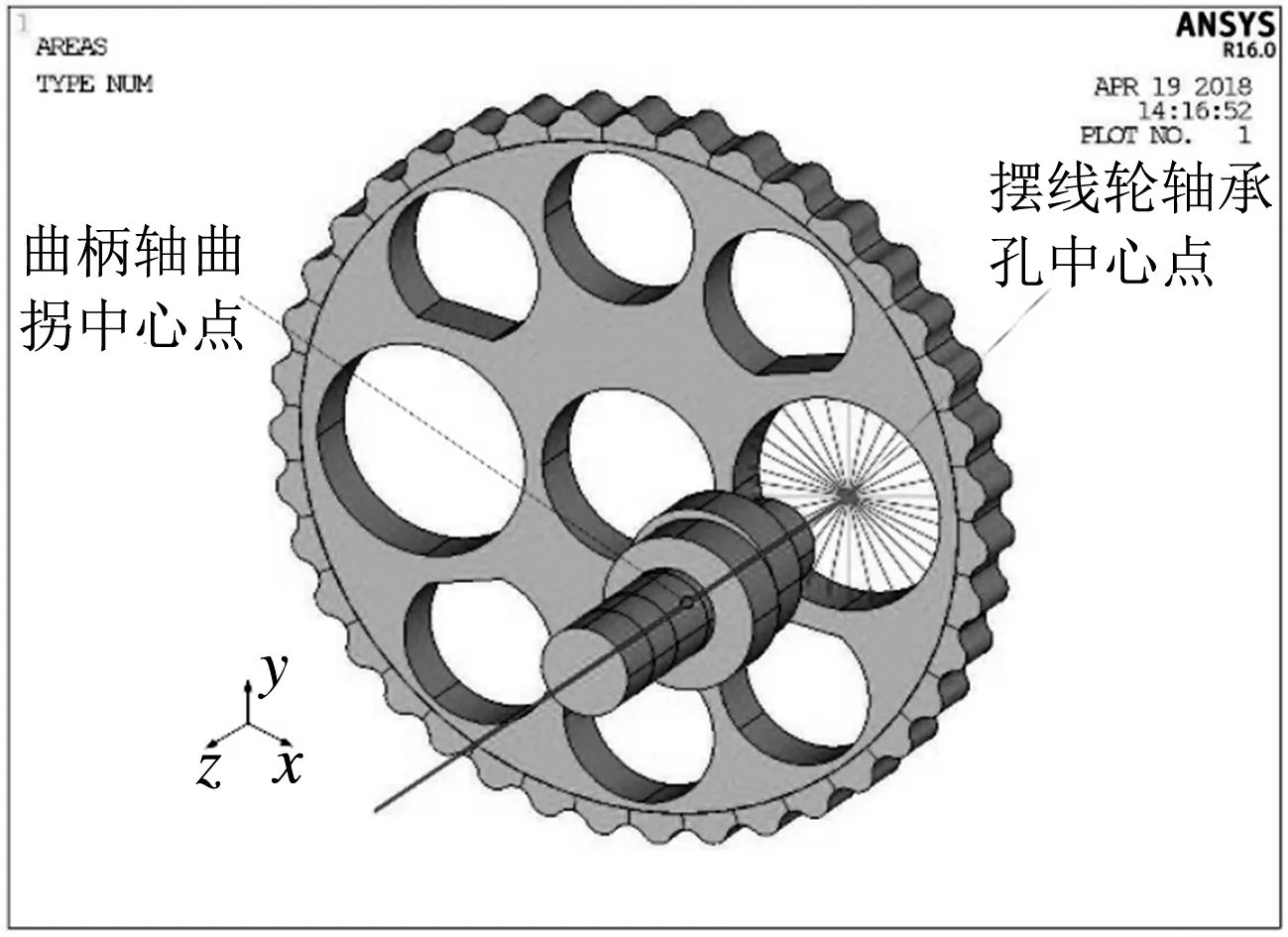
圖3 軸承模擬連接
對于擺線輪輻和針齒殼等遠離擺線輪齒嚙合區的部位,對結果影響較小,用稀疏的網格劃分代替,以節省計算機資源.這樣就導致了這樣情況的發生:擺線輪齒的網格密度和擺線輪輻的網格密度發生不連續、針齒的網格密度與針齒殼的網格密度發生不連續.為了將密度不相同的網格區域“系”在一起,ANSYS提供了一種方法,即在接觸面上生成若干約束方程,可將一個區域(網格較密)的已選節點與另一個區域(網格較疏)的已選單元連接起來生成耦合約束方程[13].如圖4所示,較密網格的擺線輪齒底部節點被“系”在了較疏網格的擺線輪輻外緣單元上;較密網格的針齒周邊節點被“系”在了較疏網格的針齒殼針齒槽里的單元上,進而形成了擺線輪整體有限元零件和針齒殼整體有限元零件.
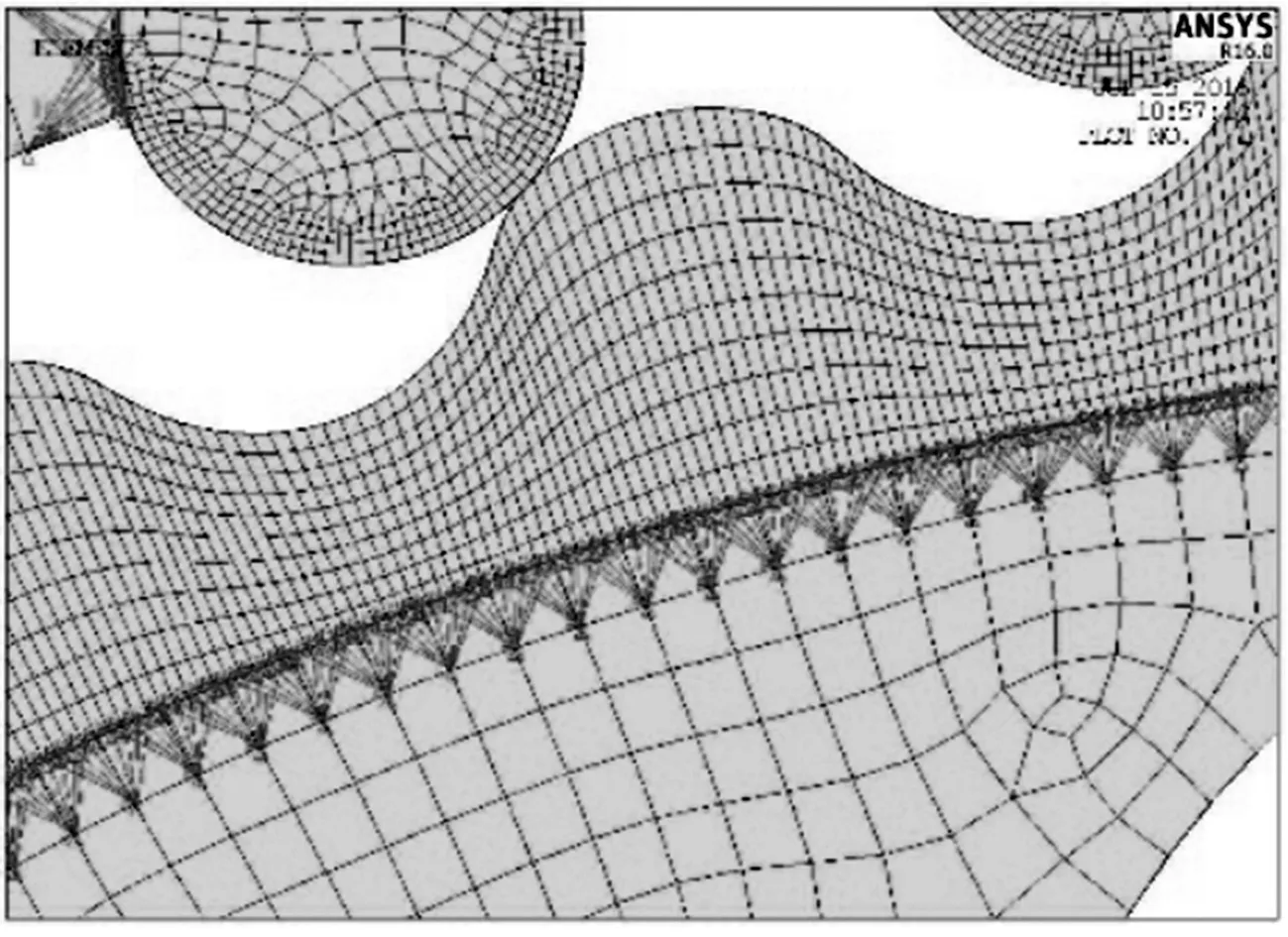
圖4 擺線輪齒耦合
擺線齒廓應用Area面生成命令,生成擺線輪齒端面,再由擺線輪齒端面拉伸出擺線輪齒實體,應用六面體單元Solid185單元并應用掃略法直接生成擺線輪齒有限元模型,注意到,由于擺線輪齒的有限元網格劃分的精度對有限元計算結果影響很大,同時擺線輪齒上的接觸應力計算結果是本文所要分析的重點,故對擺線輪齒的有限元網格進行了細化處理,擺線齒廓上的網格劃分段數為50段,網格邊線長度為0.3 mm,可見擺線輪齒網格劃分的精度很高.在針擺傳動中,因為針齒與擺線輪齒直接發生接觸,同樣為了提高有限元計算結果精度,為了節省計算資源,局部細化針齒的一條邊上的網格精度,如圖5所示.
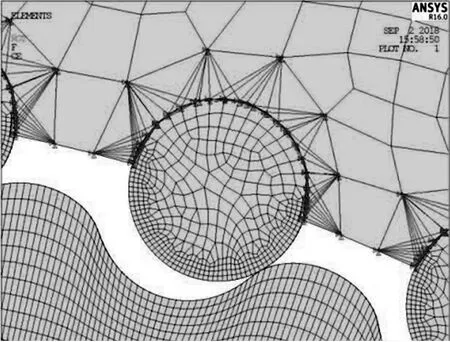
圖5 擺線輪齒有限元模型
將各個有限元零件的文件全部導入(Import)到一個最終的裝配體文件中,行星架和針輪的中心要與整體坐標系的z軸相重合,得到的RV減速器擺線針輪傳動有限元裝配模型如圖6所示.

圖6 整機有限元模型
2.2 邊界條件的確定
RV減速器的工作方式有多種,圖7所示是采用針齒殼固定,太陽輪作為RV減速器輸入端,行星架作為輸出端;圖8所示是采用行星架固定,太陽輪作為RV減速器的輸入端,針齒殼作為輸出端.對于RV減速器擺線針輪傳動部分的有限元動態仿真,其仿真的方式采用圖8所示方式.故施加邊界條件時,對于行星架來說,約束行星架結構的四周角節點上的全部自由度;對于曲柄軸來說,選取其輸入端上的全部節點,釋放這些節點的切向自由度并約束徑向自由度,對其施加逆時針方向的旋轉驅動位移;對于針齒殼來說,選取針齒殼最外圈上的全部節點,釋放這些節點的切向自由度并約束徑向自由度,因只有一片擺線輪參與嚙合,對針齒殼施加順時針方向的額定工作轉矩206 N·m.

圖7 針齒殼固定,行星架輸出

圖8 行星架固定,針齒殼輸出
3 結果分析
3.1 有限元求解
由于定義的邊界條件為行星架固定,針齒殼做輸出,因此當輸入軸定義勻速轉動時,擺線輪做平面運動,針齒殼以設定的傳動比降速輸出.
設置求解控制選項為:動態小變形求解分析項,求解輸出為最后一個載荷步的有限元計算結果;設置求解載荷步數為5,載荷步數自動劃分選項打開,最大求解載荷步數為10步,最小求解載荷步數為3步,求解時間取為系統默認的時間1s.求解在一個針擺嚙合周期內,各個針擺嚙合受力的結果.
3.2 有限元結果分析
根據擺線針輪傳動的動態嚙合過程,曲柄軸每轉動一圈,擺線輪相對于針輪轉過一個輪齒,受力區會輪流經過所有擺線輪齒.假設擺線輪輪輻為剛性,則在曲柄軸的每一個轉角位置,相應的擺線針輪傳動的最大接觸應力值都是相同的,即最大接觸應力值不隨著曲柄軸轉角的變化而變化.實際的擺線輪輻是彈性體,它在擺線輪齒受力后會產生彈性變形,擺線輪齒下方的輪輻有薄厚之分,則在曲柄軸的每一個轉角位置,輪輻的變形導致了接觸狀態的改變,因而最大接觸應力值隨著曲柄軸轉角的變化而變化.通過施加上述所確定的邊界條件,進行有限元動態嚙合仿真,可得到RV減速器擺線針輪傳動的最大接觸應力值隨曲柄軸轉角變化的歷程曲線,如圖9所示.
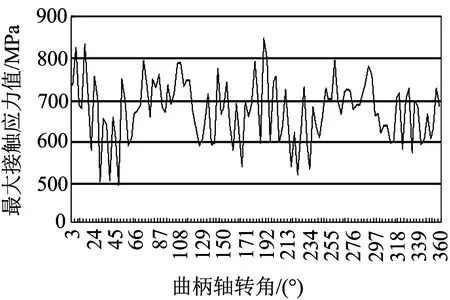
圖9 最大接觸應力值隨曲柄軸轉角變化歷程曲線
分析圖10所示的歷程曲線,從曲線可以看出:最大接觸力值隨著曲柄軸轉角的增加而呈現出上下波動的趨勢,波動的最大接觸應力值在850 MPa左右,曲柄軸的轉角為189°,波動的最小接觸應力值在500 MPa左右;波動的曲線存在明顯的周期性,即曲柄軸轉角在0~180°的范圍內為第一個周期,曲柄軸轉角在180°~360°的范圍內為第二個周期,呈類似的周期性變化.圖10為曲柄轉動在150°、189°時擺線針輪的嚙合狀態.
(a)曲柄軸轉角150°
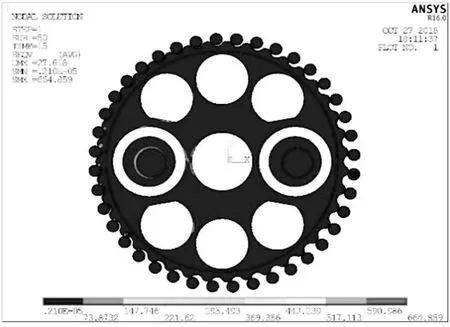
以曲柄軸轉角位置在189°時的有限元應力分析結果,圖11為擺線輪在嚙合力的作用下(求解結果放大150倍),擺線輪輪輻的受力變形情況,可以看出由于行星架連接孔的存在,薄輪輻區域在嚙合力的作用下發生了較大的彈性變形,最大等效應力為543.08 MPa.在擺線輪受力時,輪輻比較薄的部位擺線輪齒所受到的嚙合力相比于理論值就比較小,稱為擺線輪柔性區;輪輻比較厚的部位承擔了幾乎全部的工作載荷,將擺線輪輪輻比較厚的部位稱為擺線輪剛性區.圖12為在該曲柄軸轉角位值,出現最大接觸應力值的擺線輪齒嚙合接觸斑,可以看出該輪齒上的最大接觸應力為847.87 MPa,因為擺線輪齒邊緣具有一定的應力集中因素的影響,從接觸斑上的接觸應力分布可以看出,最大接觸應力主要分布在擺線輪齒面的邊緣附近處,可以猜測出此位置可能是擺線輪齒發生疲勞破壞的危險點.
圖11 擺線輪Von Stress應力

圖12 擺線輪齒接觸斑
圖13為針齒滾過一個擺線輪齒的表面,其表面接觸應力的變化歷程,每一個接觸位置都對應一個接觸斑和接觸應力值.按照圖示滑動方向,接觸斑由輪齒底部沿齒廓曲線移動變化,最大接觸應力值為847 MPa.
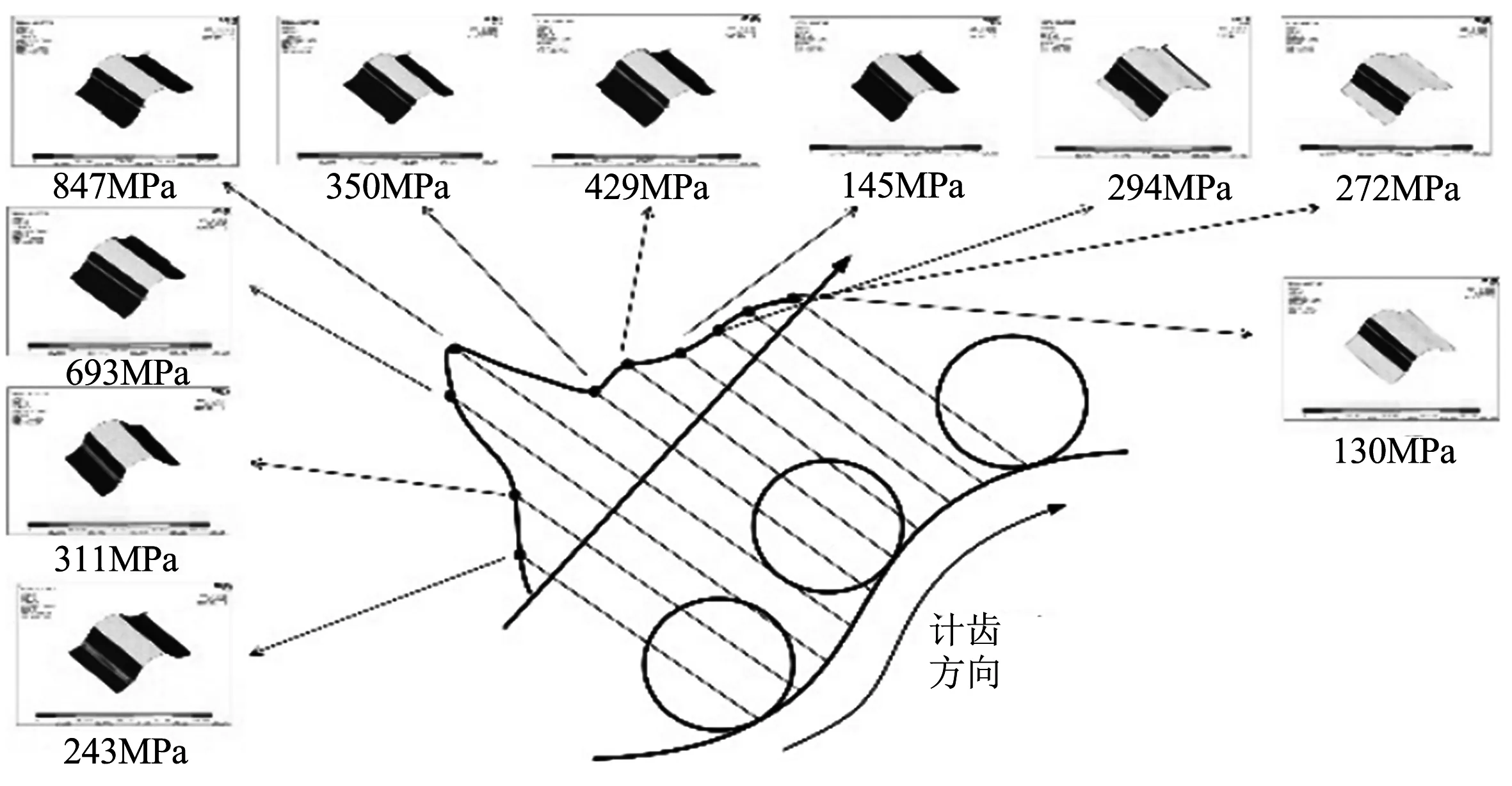
圖13 針齒沿擺線輪齒根到齒頂接觸應力大小
3.3 擺線輪嚙合力結果對比分析
根據參考文獻[4]中的計算公式,通過編寫計算程序,迭代計算得到RV減速器擺線針輪行星傳動的理論嚙合力,將其數值與有限元仿真得到的結果進行對比,如表2.

表2 擺線針輪傳動捏嚙合力對比圖表
從表中可知,因為擺線輪輪輻的剛性區和柔性區的存在,導致了擺線輪在受力的時候出現了變形分化,1號~6號擺線輪齒下方的輪輻因為處在剛性區而發生較小的彈性變形,7號~9號擺線輪齒下方的輪輻因為處在柔性性區而發生相對較大的彈性變形.擺線輪在受力的時候,柔性區的擺線輪輻被拉直從而導致擺線輪齒與針齒的接觸較輕,故得到的有限元應力仿真結果比理論值小很多;剛性區的擺線輪輪輻因為柔性區輪輻的變形,而被擠得向外凸起,從而導致擺線輪齒與針齒的接觸較重,故得到的有限元應力仿真結果比理論值結果大,兩段曲線最大值相差約160MPa.2號~6號擺線輪齒成為擺線輪主要受力輪齒,也是擺線輪的主要承載區,因此通過與理論計算結果的比較可以說明有限元仿真得到的結果更接近于實際受力情況,兩段受力曲線總體變化趨勢較為接近.
4 結論
(1)應用APDL參數化編程語言建立了RV-40E有限元分析模型,進行以針齒殼為輸出時曲柄軸轉動360°一個針擺嚙合小周期的有限元動態仿真;
(2)得到了針擺傳動的最大接觸應力隨曲柄軸轉角變化的歷程曲線,分析了針齒沿擺線輪齒根到齒頂連續動態嚙合的接觸應力變化規律,與計算得到的RV減速器擺線針輪傳動理論嚙合力進行對比,符合接觸應力的變化規律;
(3)基于APDL語言建立的參數化有限元模型可快速建立RV-E系列各個型號擺線針輪傳動動態接觸仿真模型,為理論研究提供方便.

