基于深度先驗(yàn)及非局部相似性的壓縮感知核磁共振成像

宗春梅，張?jiān)虑伲芙ǚ迹w青杉

（1.忻州師范學(xué)院計(jì)算機(jī)系，山西忻州 034000；2.太原理工大學(xué)計(jì)算機(jī)科學(xué)與技術(shù)學(xué)院，太原 030024）

（*通信作者電子郵箱zongcm123@163.com）

0 引言

壓縮感知核磁共振成像（Compressed Sensing Magnetic Resonance Imaging，CSMRI）是指通過(guò)觀測(cè)的高度欠采樣的k空間數(shù)據(jù)（圖像的傅里葉變換，也稱測(cè)量數(shù)據(jù)）重建原始圖像［1］。在采樣矩陣滿足某種條件下，該技術(shù)能夠從遠(yuǎn)低于奈奎斯特采樣率的k空間數(shù)據(jù)中精確恢復(fù)原始圖像［2］。CSMRI理論一經(jīng)提出就以采樣時(shí)間短、存儲(chǔ)數(shù)據(jù)少的優(yōu)點(diǎn)得到了學(xué)者們的關(guān)注。如何從少量的測(cè)量數(shù)據(jù)中高質(zhì)量地恢復(fù)原始圖像是CSMRI 領(lǐng)域面臨的一大挑戰(zhàn)。CSMRI 僅利用部分測(cè)量數(shù)據(jù)即包含少量信息的觀測(cè)數(shù)據(jù)進(jìn)行圖像重建，該問(wèn)題有無(wú)數(shù)個(gè)解，是一個(gè)病態(tài)問(wèn)題。解決該問(wèn)題的一個(gè)有效方式是利用圖像固有的先驗(yàn)知識(shí)進(jìn)行圖像重建。近些年來(lái)，國(guó)內(nèi)國(guó)外涌現(xiàn)出了大量的CSMRI 算法。根據(jù)算法利用的先驗(yàn)知識(shí)大致可以分為三大類：基于稀疏性的算法［3-5］、基于非局部相似性的算法［6-8］、基于深度先驗(yàn)的算法［9-12］。

基于稀疏性的算法是利用圖像在變換域或者字典下的稀疏性進(jìn)行圖像重建。其中，稀疏性又可以分為全局稀疏性和局部稀疏性。全局稀疏性是指圖像在梯度域、小波變換域、緊標(biāo)架下的稀疏性，而局部稀疏性是指圖像塊在固定字典或自適應(yīng)字典下的稀疏性。基于全局稀疏性的方法重建速度相對(duì)較快，但是重建質(zhì)量有待提高。基于局部稀疏性的方法通過(guò)字典學(xué)習(xí)技術(shù)進(jìn)行圖像重建［5］，利用交替優(yōu)化的方式在迭代過(guò)程中聯(lián)合優(yōu)化圖像和字典。相較于基于全局稀疏性的方法，該類方法能夠?qū)W習(xí)自適應(yīng)字典，重建質(zhì)量高，但成像速度相對(duì)較低。

基于非局部相似性的CSMRI 算法是利用非局部區(qū)域內(nèi)圖像塊之間的相似性進(jìn)行重建，本質(zhì)是圖像的當(dāng)前塊估計(jì)通過(guò)一定區(qū)域內(nèi)的相似塊加權(quán)得到。近些年，利用塊匹配三維濾波（Block Matching and 3D Filtering，BM3D）高斯去噪器［13］隱式利用非局部相似性進(jìn)行圖像重建得到了學(xué)者們的關(guān)注。Eksioglu［6］利用BM3D 去噪器構(gòu)建了去耦合的CSMRI 框架，該框架能夠隱式地利用BM3D 去噪器包含的圖像先驗(yàn)知識(shí)，即圖像的非局部相似性及圖像在三維小波變換下的稀疏性。Shi 等［7］利用BM3D 去噪器構(gòu)建了正則化模型，并用于提升基于局部稀疏性的CSMRI 算法重建質(zhì)量。實(shí)驗(yàn)結(jié)果表明該類方法能夠獲得較高質(zhì)量的圖像。

基于深度先驗(yàn)的算法是通過(guò)深度神經(jīng)網(wǎng)絡(luò)進(jìn)行圖像重建。Yang 等［9］利用交替方向乘子法（Alternating Direction Method of Multipliers，ADMM）求解構(gòu)建的CSMRI 優(yōu)化問(wèn)題，并將求解框架展開(kāi)成網(wǎng)絡(luò)，提出了ADMM-CSNet（Alternating Direction Method of Multipliers-Compressed Sensing Network）算法。ADMM-CSNet算法能夠通過(guò)事先訓(xùn)練好的深度神經(jīng)網(wǎng)絡(luò)進(jìn)行快速成像且取得較好的重建效果。基于深度先驗(yàn)的算法雖然能夠取得較好的性能，但是該類直接訓(xùn)練端到端深度神經(jīng)網(wǎng)絡(luò)的方法泛化能力差，且不具可解釋性。

上述算法雖然取得了較好的重建效果，但在低采樣率時(shí)，重構(gòu)質(zhì)量仍然有提升空間。不同于上述算法，本文利用深度先驗(yàn)和非局部相似性進(jìn)行壓縮感知核磁共振成像。本文利用深度去噪器和BM3D 去噪器通過(guò)即插即用模型將這兩種先驗(yàn)知識(shí)引入到圖像重建中。受基于深度先驗(yàn)的稀疏表示模型［14］啟發(fā)，本文提出基于兩種去噪器的稀疏表示模型。該模型能夠融合深度先驗(yàn)、圖像的非局部相似性及圖像在三維變換下的稀疏性進(jìn)行圖像重建。結(jié)合該模型與數(shù)據(jù)保真模型構(gòu)建CSMRI 優(yōu)化問(wèn)題，利用交替優(yōu)化的方式對(duì)該問(wèn)題進(jìn)行有效求解。本文利用多種先驗(yàn)知識(shí)進(jìn)行成像期望得到高質(zhì)量的圖像重建。

1 基于稀疏性的壓縮感知核磁共振成像

假設(shè)原始核磁共振圖像為x∈RN，CSMRI 采樣模型可描述為

其中：Fu∈Cm×N（m＜N）表示欠采樣傅里葉編碼矩陣，也即欠采樣算子；ratio=m/N定義為采樣率；y∈Cm表示觀測(cè)的k空間數(shù)據(jù)即測(cè)量數(shù)據(jù)；n∈Cm表示高斯噪聲向量。如何利用測(cè)量數(shù)據(jù)y重建原始圖像x是CSMRI算法所要解決的問(wèn)題。

基于全局稀疏性的CSMRI算法通常構(gòu)建以下優(yōu)化問(wèn)題：

其中：ψ是某種全局變換；λ為正則化參數(shù)。||·||p表示lp范數(shù)：p=0時(shí)，即為l0偽范數(shù)，衡量對(duì)應(yīng)向量中非零元素的個(gè)數(shù)；當(dāng)p=1 時(shí)，||·||p為l1范數(shù)，表示對(duì)應(yīng)向量中每個(gè)元素絕對(duì)值的和。上述優(yōu)化問(wèn)題可通過(guò)梯度下降法、變量分離法或其加速方法進(jìn)行求解。基于全局稀疏性的方法能夠快速進(jìn)行圖像重建，但由于全局變換是固定的，重建質(zhì)量有待提升。

不同于上述算法，基于局部稀疏性的CSMRI 算法通常利用自適應(yīng)字典進(jìn)行重建。在重建過(guò)程中，通過(guò)估計(jì)圖像學(xué)習(xí)自適應(yīng)字典。該類方法通常構(gòu)建以下優(yōu)化問(wèn)題［5］：

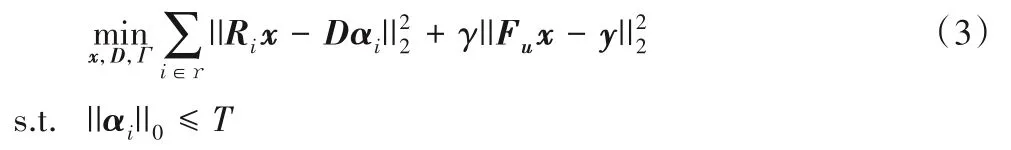
其中：?是圖像塊索引的集合；Ri∈RB×N表示取塊算子；γ是平衡參數(shù)；D∈CB×K表示待訓(xùn)練的塊字典；αi∈CK表示圖像塊Rix在字典D下的表示系數(shù)；Γ是所有表示系數(shù)的集合；T為稀疏度。上述優(yōu)化問(wèn)題通常利用交替優(yōu)化的方式分字典學(xué)習(xí)和圖像更新兩步進(jìn)行求解。由于字典能夠通過(guò)測(cè)量數(shù)據(jù)進(jìn)行訓(xùn)練，學(xué)習(xí)的字典能夠?qū)χ亟▓D像自適應(yīng)稀疏表示。基于字典學(xué)習(xí)的CSMRI 算法較基于全局變換的CSMRI 算法重建質(zhì)量高。

為進(jìn)一步提升重建質(zhì)量，Eksioglu［6］利用BM3D 去噪器隱式利用隱含在BM3D 去噪器中的先驗(yàn)知識(shí)進(jìn)行圖像重建，提出了基于三維塊匹配的核磁共振成像算法BM3D-MRI（Block Matching and 3D filtering-Magnetic Resonance Imaging）算法。該算法構(gòu)建以下去耦合的CSMRI 優(yōu)化框架（對(duì)于第t次迭代）：

其中：ΦBM3D表示BM3D 去噪器對(duì)應(yīng)的解析稀疏算子［6］。式（4）可通過(guò)求導(dǎo)并令導(dǎo)數(shù)為0 獲得閉式解，式（5）直接利用BM3D 去噪器近似求解。由于上述框架在優(yōu)化過(guò)程中利用BM3D 去噪器對(duì)估計(jì)圖像進(jìn)行去噪處理，該框架能夠隱含地利用非局部相似性。

受上述算法及基于深度先驗(yàn)的稀疏表示模型［14］啟發(fā)，本文通過(guò)BM3D 去噪器和深度去噪器相結(jié)合，提出融合多種先驗(yàn)知識(shí)的CSMRI 算法。本文構(gòu)建了基于多種去噪器的稀疏表示模型，該模型能夠?qū)⒍喾N去噪器蘊(yùn)含的先驗(yàn)知識(shí)融合到圖像重建中。多種先驗(yàn)知識(shí)的利用能夠提升低采樣率下的重建質(zhì)量。

2 基于多種去噪器的稀疏表示模型

如何利用多種先驗(yàn)知識(shí)進(jìn)行CSMRI 是本文解決的一個(gè)關(guān)鍵問(wèn)題。本文利用兩種不同的去噪器構(gòu)建稀疏表示模型以利用多種先驗(yàn)知識(shí)。傳統(tǒng)稀疏表示模型假定圖像x在標(biāo)架或某種變換W下是稀疏的，通常構(gòu)建以下優(yōu)化模型以求解稀疏表示系數(shù)［15］：

其中參數(shù)η控制稀疏程度。對(duì)于任意變換W，上述優(yōu)化模型可以通過(guò)迭代閾值方法求解。為了降低計(jì)算復(fù)雜度，本文將緊約束施加到標(biāo)架W上，即W為緊標(biāo)架WTW=I。基于緊標(biāo)架的優(yōu)化問(wèn)題（6）可直接通過(guò)簡(jiǎn)單的閾值方法求解。圖像經(jīng)過(guò)BM3D 去噪器的濾波圖像在緊標(biāo)架下的表示系數(shù)與原始圖像在同一緊標(biāo)架下的表示系數(shù)應(yīng)該是近似的，兩個(gè)系數(shù)向量的差值應(yīng)是稀疏的。基于該認(rèn)識(shí)，本文構(gòu)建基于多種去噪器的稀疏表示模型，優(yōu)化模型可表示為：

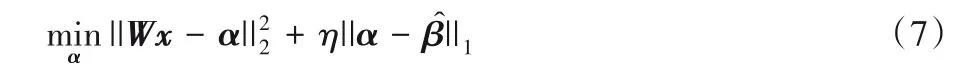
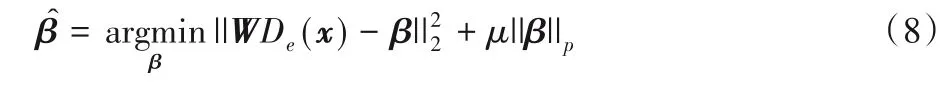
其中：De(x)表示利用去噪器對(duì)圖像x進(jìn)行濾波；μ表示稀疏正則化參數(shù)，用以控制濾波圖像在緊標(biāo)架下的稀疏程度。De(x)可以是單個(gè)去噪器，也可以是多種去噪器的加權(quán)求和即表示第j個(gè)去噪器對(duì)圖像進(jìn)行濾波以后的圖像）。文獻(xiàn)［14］指出利用不同的高斯去噪器可以將不同的先驗(yàn)知識(shí)引入到圖像重建中。本文利用兩種去噪器構(gòu)建該模型，即深度去噪器與BM3D 去噪器。在這種情況下，濾波圖像可表示為。其中，Deep(x)表示利用深度去噪器對(duì)圖像進(jìn)行濾波，BM3D(x)表示利用BM3D 去噪器對(duì)圖像進(jìn)行濾波。本文聯(lián)合采用這兩種去噪器，試圖融合兩種去噪器在去噪或?yàn)V波過(guò)程中利用的先驗(yàn)知識(shí)進(jìn)行圖像重建。深度高斯去噪器利用深度先驗(yàn)進(jìn)行圖像去噪，利用該去噪以將深度先驗(yàn)引入到圖像重建中。深度去噪器通常未充分利用圖像的自相似性，BM3D 去噪器彌補(bǔ)了該不足，該去噪器通過(guò)利用非局部區(qū)域內(nèi)的相似性先驗(yàn)知識(shí)進(jìn)行圖像去噪。本文利用這兩種去噪器進(jìn)行聯(lián)合去噪或?yàn)V波以期望利用深度先驗(yàn)和非局部相似性先驗(yàn)的互補(bǔ)性進(jìn)行高質(zhì)量圖像重建。

式（8）可通過(guò)對(duì)濾波圖像在緊標(biāo)架下的表示系數(shù)進(jìn)行閾值處理求解。如果p=1，則，此時(shí)表示閾值為的軟閾值算子，定義為T[·，ε]=soft{·，ε}=sign(·)max(|·|-ε，0)，sign(·)為符號(hào)函數(shù)，max(·)為取最大值算子。如果p=0，則，此時(shí)表示硬閾值算子，定義為：如果，否則。需要指出的是，閾值算子操作是逐元素進(jìn)行的，因此上述對(duì)向量的處理是對(duì)每一元素進(jìn)行閾值處理。

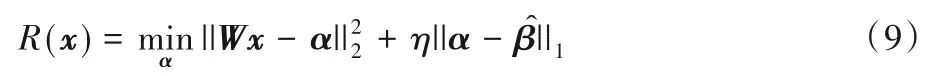
構(gòu)建的上述正則化模型R(x)是一個(gè)包絡(luò)函數(shù)，可以直接作為正則項(xiàng)引入到成像的優(yōu)化模型中。式（9）中的第一項(xiàng)表示圖像在緊標(biāo)架下的表示系數(shù)近似為α，第二項(xiàng)表示該系數(shù)逼近于輔助系數(shù)向量。其中該輔助系數(shù)向量的更新能夠通過(guò)兩種去噪器將深度先驗(yàn)、非局部相似性及三維變換下的稀疏性隱式地進(jìn)行利用。由于式（9）中的輔助系數(shù)向量可通過(guò)求解式（8）獲得，故基于BM3D 去噪器的稀疏表示正則化模型可寫成以下簡(jiǎn)潔的形式：

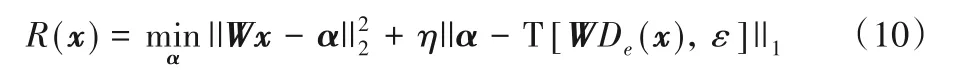
構(gòu)建的正則化模型（10）具有以下優(yōu)點(diǎn)：

1）有效。該正則化模型能夠通過(guò)多種去噪器利用多種互補(bǔ)先驗(yàn)知識(shí)進(jìn)行圖像重建，多種先驗(yàn)知識(shí)有益于圖像重建；

2）靈活。該模型的靈活性主要體現(xiàn)在以下兩個(gè)方面：第一，去噪器可以換成其他有效的去噪器以利用不同的先驗(yàn)知識(shí)進(jìn)行圖像重建；第二，該正則化模型可用于其他成像應(yīng)用，不局限于壓縮感知核磁共振成像。

3 融合深度先驗(yàn)及非局部相似性的CSMRI

本文利用基于兩種去噪器的稀疏表示模型進(jìn)行壓縮感知核磁共振成像以解決現(xiàn)有CSMRI 算法重建質(zhì)量低的問(wèn)題，構(gòu)建以下優(yōu)化模型：

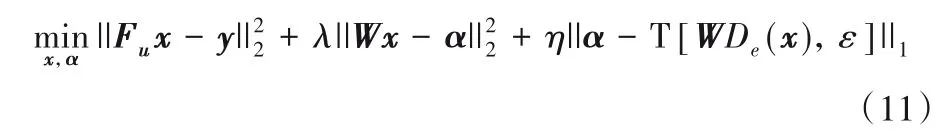
式（11）代價(jià)函數(shù)中：第一項(xiàng)為數(shù)據(jù)保真項(xiàng)，保證重建的圖像與測(cè)量數(shù)據(jù)y相匹配；第二、三項(xiàng)為本文構(gòu)建的基于多種去噪器的稀疏表示模型。由于上述代價(jià)函數(shù)采用l2范數(shù)和l1范數(shù)，如果固定輔助系數(shù)向量T[WDe(x)，ε]，所對(duì)應(yīng)的優(yōu)化是一個(gè)凸優(yōu)化問(wèn)題。然而，由于閾值算子（閾值算子是非凸的）和多種去噪器（去噪器可看成去噪函數(shù)，通常是非凸的）存在于最后一項(xiàng)，上述優(yōu)化問(wèn)題在考慮x和α聯(lián)合優(yōu)化時(shí)，該問(wèn)題是一個(gè)復(fù)雜的非凸優(yōu)化問(wèn)題。為了對(duì)其進(jìn)行有效求解，本文假設(shè)濾波圖像De(x)近似于估計(jì)圖像的濾波圖像De(x(t-1))，即De(x)≈De(x(t-1))。基于該假設(shè)，優(yōu)化問(wèn)題（11）可改寫為（對(duì)于第t次迭代）：

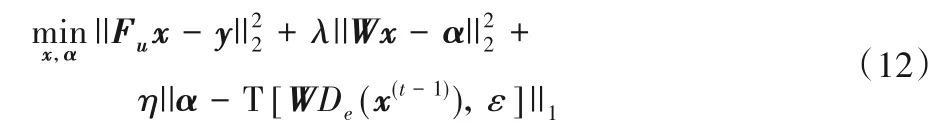
利用交替優(yōu)化的方法求解上述優(yōu)化問(wèn)題，對(duì)于第t次迭代，分為以下兩步對(duì)問(wèn)題（12）進(jìn)行求解：

1）系數(shù)更新步驟，固定估計(jì)圖像x(t-1)，更新稀疏系數(shù)α(t)的子問(wèn)題為：

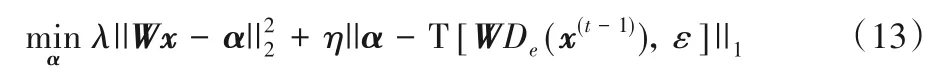
上述優(yōu)化問(wèn)題可通過(guò)軟閾值算子進(jìn)行求解：

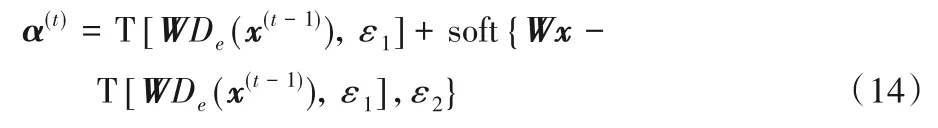
實(shí)驗(yàn)結(jié)果表明，T[·，ε1]采用硬閾值算子成像效果優(yōu)于利用軟閾值算子，因此本文采用硬閾值算子。對(duì)濾波圖像在緊標(biāo)架下的表示系數(shù)進(jìn)行硬閾值處理，得到輔助系數(shù)向量T[WDe(x(t-1))，ε1]。

2）圖像更新步驟，固定稀疏系數(shù)α(t)，更新圖像x(t)的子問(wèn)題為：

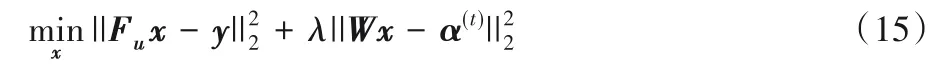
對(duì)式（15）中的代價(jià)函數(shù)求導(dǎo)，并令導(dǎo)數(shù)為零：

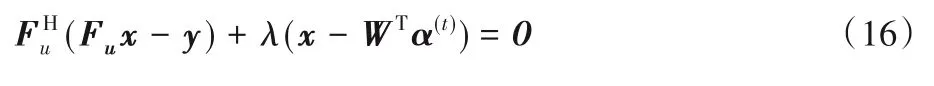
傅里葉變換矩陣F∈CN×N通常為酉矩陣，滿足FHF=I。根據(jù)這一等式，式（16）可改寫為：

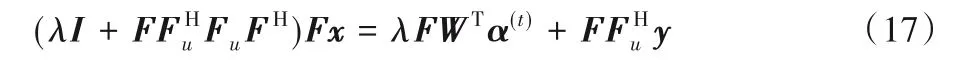
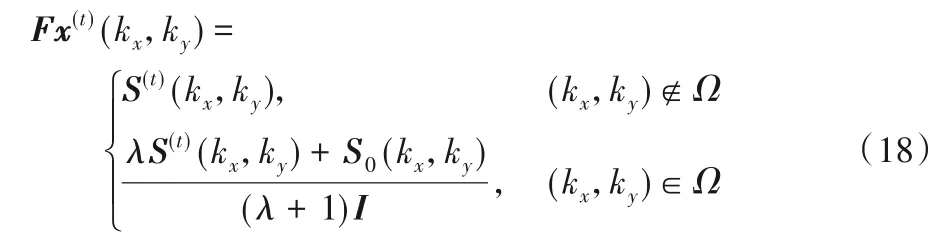
其中：Fx(t)(kx，ky)表示在位置(kx，ky)的更新值；Ω是被采樣的k空間數(shù)據(jù)的集合。最后對(duì)Fx(t)進(jìn)行傅里葉反變換，獲得最終圖像重建結(jié)果。

交替優(yōu)化稀疏系數(shù)與圖像直到達(dá)到終止條件可以得到優(yōu)化問(wèn)題（11）的一個(gè)近似解。本文算法如下：

4 實(shí)驗(yàn)與結(jié)果分析

為了驗(yàn)證本文算法的有效性，本文采用了6 幅大小為256 × 256 的核磁共振圖像作為測(cè)試圖像進(jìn)行壓縮感知核磁共振成像實(shí)驗(yàn)，測(cè)試圖像分別為Brain、Shoulder、Bone、Head、Bust、Brain2。采用偽隨機(jī)采樣算子對(duì)k空間數(shù)據(jù)進(jìn)行欠采樣，圖1給出了采樣算子和6幅原始圖像。所有算法均在配置為Core i7-7700 主頻3.6 GHz CPU，內(nèi)存8 GB 的PC 上進(jìn)行測(cè)試，軟件平臺(tái)為Windows 10 64 位操作系統(tǒng)，Matlab 2018b。為了模擬更真實(shí)的采樣環(huán)境，本文對(duì)采樣值施加噪聲標(biāo)準(zhǔn)差為σ=1 的噪聲。本文算法在不同采樣率情況下與基于小波樹(shù)稀疏性的核磁共振成像算法WaTMRI（Magnetic Resonance Imaging with Wavelet Tree sparsity）［4］、基于字典學(xué)習(xí)的核磁共振成像算法 DLMRI（Dictionary Learning for Magnetic Resonance Imaging）［5］、基于字典更新及塊匹配和三維濾波的核磁共振成像算法（Magnetic Resonance Imaging based on Dictionary Updating and Block Matching and 3D filtering，DUMRI-BM3D）［7］、BM3D-MRI 算法［6］、廣義近似消息傳遞去噪算法DAMP（Denoising Approximate Message Passing）［8］進(jìn)行對(duì)比，對(duì)比算法均采用軟件包中給出的默認(rèn)參數(shù)。本文分別從客觀角度和主觀視覺(jué)角度對(duì)測(cè)試算法進(jìn)行對(duì)比。采用峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）作為評(píng)價(jià)重建質(zhì)量好壞的客觀標(biāo)準(zhǔn)，主觀視覺(jué)評(píng)價(jià)則計(jì)算特征相似性（Feature SIMilarity，F(xiàn)SIM）［16］，同時(shí)給出各個(gè)算法的部分重建圖像進(jìn)行對(duì)比。PSNR 值和FSIM 值越大表明重建圖像視覺(jué)效果越好，重建質(zhì)量越高。

在實(shí)驗(yàn)中，本文的深度去噪器選用近些年比較優(yōu)秀的深度去噪器FFDNet（Fast and Flexible Denoising convolutional neural Network）［17］。輸入去噪器的噪聲標(biāo)準(zhǔn)差采用BM3DMRI 算法給出的非線性構(gòu)建方法［6］。假設(shè)該方法計(jì)算的標(biāo)準(zhǔn)差為σ，為實(shí)現(xiàn)較好的重建效果，輸入BM3D與FFDNet去噪器的噪聲標(biāo)準(zhǔn)差分別為6σ、3σ。正則化參數(shù)λ、閾值ε1及ε2均采用PSNR 值最大的準(zhǔn)則進(jìn)行調(diào)節(jié)，對(duì)于某一幅測(cè)試圖像，固定一個(gè)參數(shù)，去調(diào)節(jié)另一個(gè)參數(shù)使得獲得的PSNR 值最大。當(dāng)調(diào)到最大效果時(shí)，固定該參數(shù)，去調(diào)節(jié)另一個(gè)。閾值ε1與ε2應(yīng)與估計(jì)圖像中的噪聲標(biāo)準(zhǔn)差有關(guān)，經(jīng)驗(yàn)表明，當(dāng)λ=0.01、ε1=0.5σ、ε2=5σ時(shí)，圖像重建效果最好。當(dāng)參數(shù)調(diào)整好以后，利用這套參數(shù)對(duì)不同采樣率下、不同圖像進(jìn)行核磁共振成像。緊標(biāo)架選用離散余弦變換并使用文獻(xiàn)［14］公布的默認(rèn)參數(shù)。為了公平比較，提出的算法對(duì)于不同的采樣率選用同一套參數(shù)。為了說(shuō)明多種互補(bǔ)先驗(yàn)的有效性，本文將僅利用FFDNet 去噪器的方法作為基準(zhǔn)算法，簡(jiǎn)記為CSMRIFFDNet。

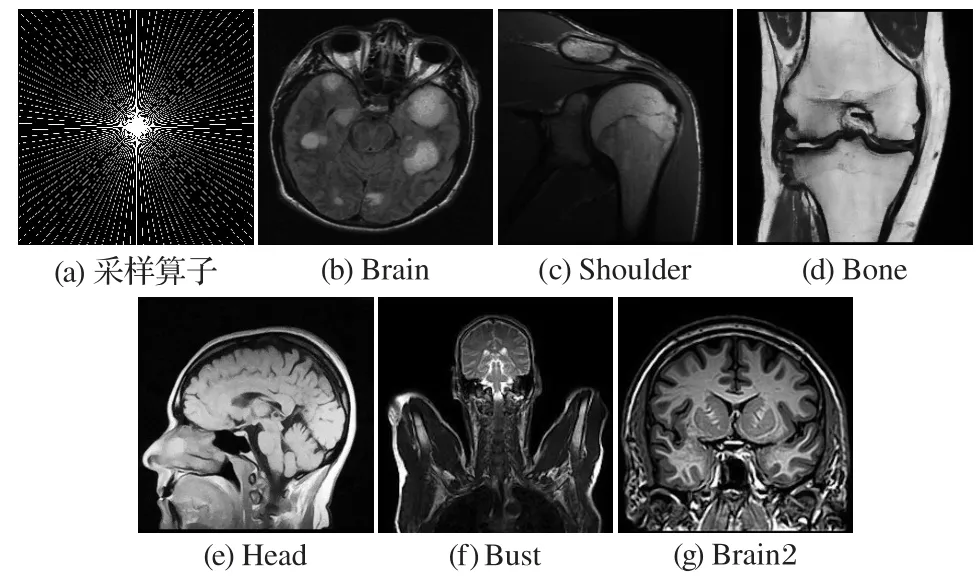
圖1 采樣算子和原始圖像Fig.1 Sampling operator and original images

表1 給出了在采樣率為0.02、0.06、0.09 及0.13 的情況下測(cè)試算法的PSNR 值（由于版面限制，本文僅給出5 種具有代表性的測(cè)試算法結(jié)果），從中可以看出：1）對(duì)于多數(shù)情況，本文算法的PSNR 值最高；2）以Brain 圖像為例，在采樣率為0.02 情況下，本文算法重構(gòu)圖像的PSNR 值比DUMRI-BM3D算法、BM3D-MRI 算法、DAMP 算法及CSMRI-FFDNet 算法分別提高了1.05 dB、0.45 dB、0.85 dB 及0.34 dB；3）在低采樣率下，本文算法仍然能夠重構(gòu)出較高PSNR 的圖像；4）利用兩種去噪器的本文算法優(yōu)于僅利用FFDNet 去噪器的CSMRIFFDNet 算法。CSMRI-FFDNet 算法利用了深度先驗(yàn)，重建平均PSNR 值優(yōu)于其他對(duì)比算法。深度先驗(yàn)并未考慮圖像非局部區(qū)域的相似性，由于本文算法能夠利用深度先驗(yàn)與非局部相似性進(jìn)行圖像重建，因此本文算法優(yōu)于僅利用深度先驗(yàn)的CSMRI-FFDNet算法。

為了進(jìn)一步衡量本文算法主觀視覺(jué)的優(yōu)點(diǎn)，表1 給出在不同采樣率下測(cè)試算法獲得的FSIM 值。從表1 中可以看出，本文算法對(duì)于不同圖像、不同采樣率都能夠獲得最高的FSIM值，也就意味著視覺(jué)效果最好。圖2 給出了測(cè)試算法對(duì)圖像Head的重建結(jié)果，從重建圖像中可以看出：WaTMRI的重建質(zhì)量最差、最模糊，含有大量的噪聲；DLMRI 算法重建圖像消除了部分噪聲，但仍然丟失了大量細(xì)節(jié)信息，并且重建圖像具有塊效應(yīng)；DUMRI-BM3D 算法、BM3D-MRI 算法及DAMP 算法消除了噪聲，但是重建圖像丟失了部分細(xì)節(jié)信息，具有明顯的偽影效應(yīng)；而本文算法消除了偽影，保留了大量細(xì)節(jié)信息，視覺(jué)效果最好。

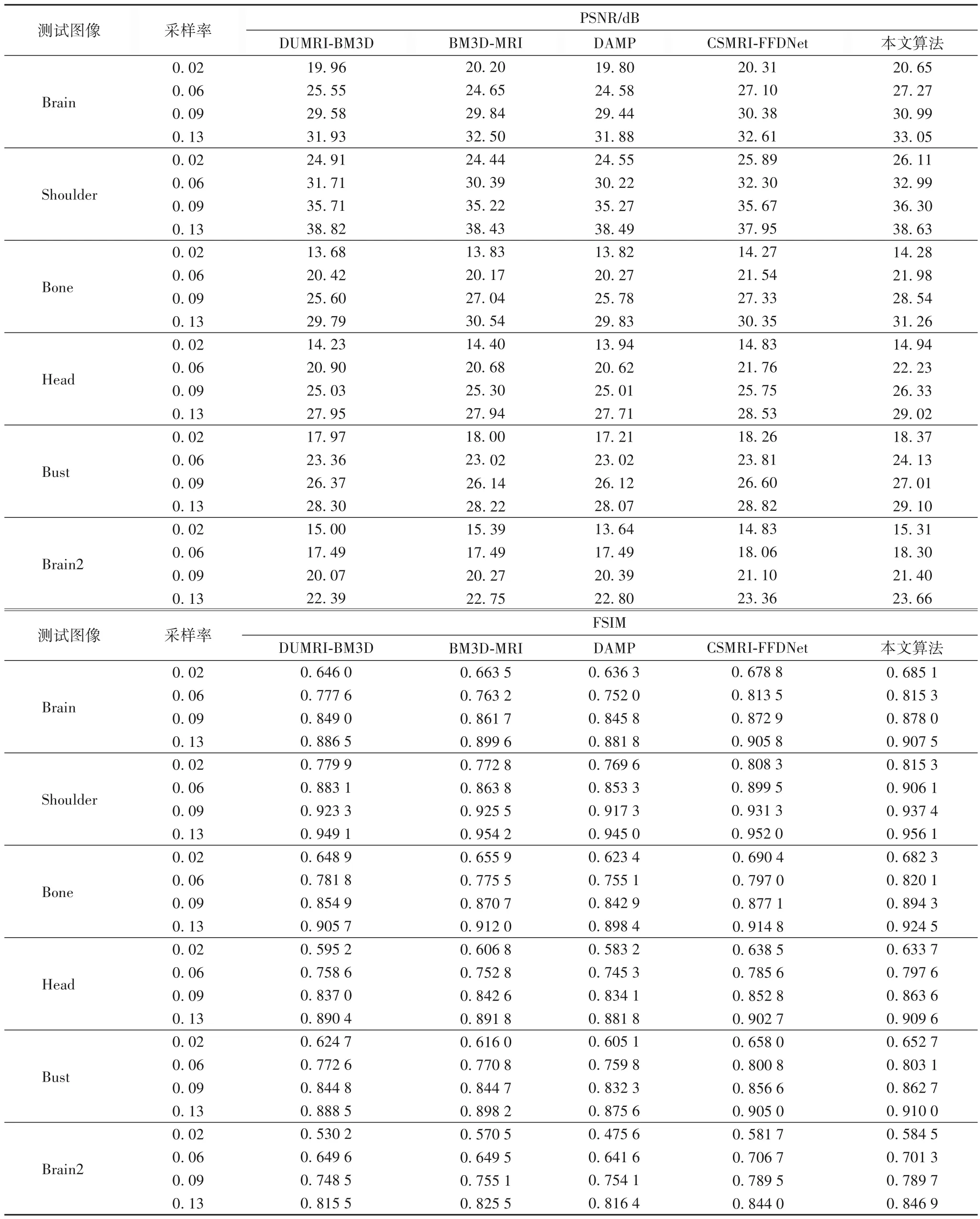
表1 不同算法PSNR值和FSIM值比較Tab.1 Comparison of PSNR and FSIM values of different algorithms

為了衡量算法的成像速度，表2 給出了測(cè)試算法的平均運(yùn)行時(shí)間，是測(cè)試算法對(duì)4 種采樣率、6 幅圖像的運(yùn)行時(shí)間平均值。從表2 可以看出，僅利用全局變換的WaTMRI 算法耗時(shí)最少，利用字典學(xué)習(xí)進(jìn)行成像的DLMRI 算法用時(shí)最多。DUMRI-BM3D 算法利用字典更新和BM3D 去噪器進(jìn)行成像，因此成像時(shí)間相對(duì)較長(zhǎng)。本文算法的運(yùn)行時(shí)間較WaTMRI算法、BM3D-MRI算法及CSMRI-FFDNet長(zhǎng)。這是因?yàn)楸疚乃惴ɡ昧讼∈璞硎竞虰M3D 去噪器。為提升成像速度，本文算法可通過(guò)并行計(jì)算進(jìn)行加速。雖然本文算法比這3 種算法耗時(shí)長(zhǎng)，但本文算法重建質(zhì)量高于這3 種算法，更加適用于低采樣率下對(duì)重建質(zhì)量要求高的場(chǎng)合。

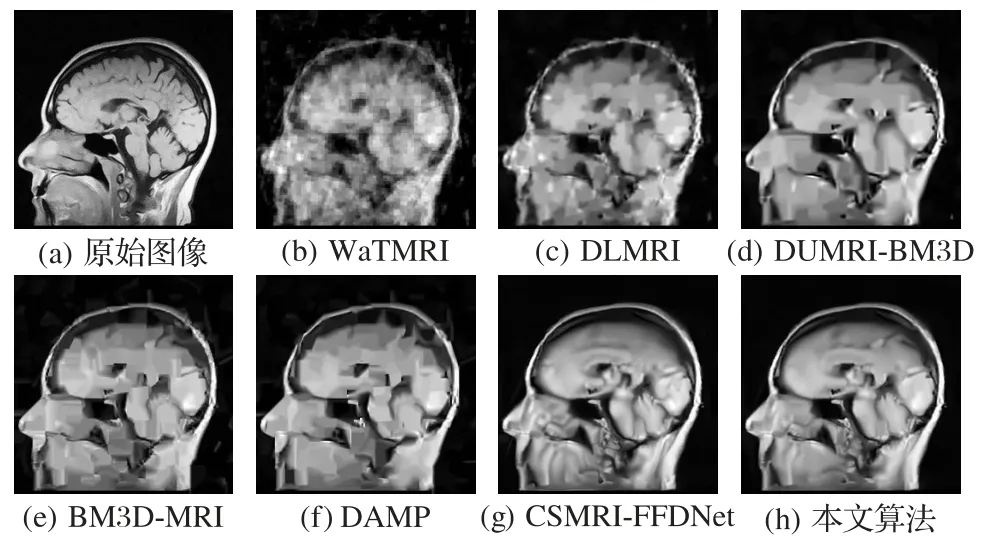
圖2 測(cè)試算法的Head重建圖像（采樣率為0.06）Fig.2 Reconstructed head images by different test algorithms（sampling ratio of 0.06）

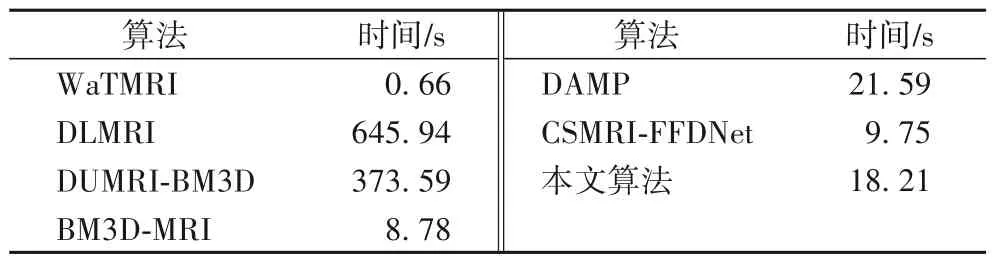
表2 不同算法的運(yùn)行時(shí)間比較Tab.2 Running time comparison of different algorithms

5 結(jié)語(yǔ)

本文針對(duì)深度先驗(yàn)和非局部相似性的互補(bǔ)性，利用基于多種去噪器的稀疏表示模型，提出了融合兩種先驗(yàn)知識(shí)的壓縮感知核磁共振圖像重構(gòu)算法。該算法將基于多種去噪器的稀疏表示模型結(jié)合到CSMRI 的代價(jià)函數(shù)中，利用交替優(yōu)化方法有效地求解了所對(duì)應(yīng)的優(yōu)化問(wèn)題。實(shí)驗(yàn)結(jié)果表明，提出的算法能夠在低采樣率下獲得較高的重建質(zhì)量，且兩種先驗(yàn)知識(shí)的融合能夠提升圖像的重建質(zhì)量。如何加速本文算法是以后的研究方向。