纖維加筋土剪切過程中顆粒運動特征研究

張福海，白巖輝*，周天寶，陳 良

(1.河海大學 巖土力學與堤壩工程教育部重點實驗室，江蘇 南京 210098；2.河海大學 江蘇省巖土工程技術工程研究中心，江蘇 南京 210098)

隨著社會的不斷發展，基礎設施的建設愈加完善，越來越多的設施建立在軟弱土、特殊土等不良地基上。在這一背景下，纖維加筋技術作為軟弱土改良技術中的一員，因其具有價格低廉、原材料來源廣泛、綠色無污染、施工工藝簡單和改良效果顯著等優點，引起了巖土工程領域的廣泛關注[1]。Jamshidi等研究了纖維長寬比與含量對加筋土板樁在地震作用下的影響，得出加筋能夠改善土板樁動力響應特性[2]。Plé等通過試驗得出纖維能夠提高黏土的初始楊氏模量、脆性指數以及內摩擦角[3]。盧凱等研究發現纖維能夠改善混凝土的強度及韌性[4]。Mirzababaei等指出低纖維含量也可能增加土體在大剪切位移下的抗剪強度[5]。Michalowsk和zhao基于纖維加筋粗粒土在破壞時纖維中部拉斷兩端滑移的假設建立了在平面應變狀態下纖維加筋土能量均化模型[6]。現有的研究更加關注纖維加筋土其抗剪強度與工程性質的研究，對纖維加固機理方面的研究關注較少[7]。本文是從剪切過程中纖維土顆粒運動特征這一角度出發，從微觀層面來分析纖維的加固機理，為纖維加固機理的研究提供些許參考價值。

1 直剪試驗計算模型與顆粒運動特征

1.1 模型的建立與參數的選擇

本文通過直剪試驗來研究剪切過程中纖維對纖維土的作用機理。因纖維在土體中分布的復雜性與直剪試驗下土體的大變形，故本文采用離散元法進行數值模擬。模型使用PFC2D(version5.0)建立，試樣尺寸為50 mm×100 mm，由11 000個二維剛性顆粒組成(不計纖維顆粒數)，如圖1所示，其顆粒粒徑滿足ASTM D3080-90的要求(即試樣的高寬與最大顆粒粒徑比值不小于6到10[8])。模型中纖維土為加纖維的膨脹土，其顆粒密度為2 790 kg/m3。膨脹土的初始孔隙比是根據何詠睿[9]的研究成果，將天然的孔隙比進行換算得到用于PFC2D模擬的孔隙比，根據實驗結果膨脹土的天然孔隙比為0.45，換算得到試樣的孔隙比為0.18。模型纖維含量為0.6%。因土體為膨脹土，故本文選用接觸粘結模型，其參數值參考現有對膨脹土模擬的參數，進行一定調整使其符合膨脹土的性質，具體參數如表1所列。模型中纖維采用接觸粘結模型，模擬不考慮纖維斷裂的影響，因此纖維的接觸粘結抗拉與抗剪強度需取一個極大的值，使纖維不會產生斷裂，本文倆值均取1e9，通過觀察模擬過程中纖維均不會產生斷裂；纖維土作為一種土工加筋技術，需要纖維的變形模量要遠大于土體的變形模量，因此模型中纖維的法相剛度與切向剛度的值取為土體的100倍與200倍。本文模擬了豎向壓力為100 kPa時素土與纖維土體兩種試樣的直剪過程，剪切位移即為剪切盒上盒移動的距離，當達到16 mm時停止剪切。

1.2 直剪的應力應變曲線

圖2為素土與纖維土在豎向壓力為100 kPa時的剪應力與剪切位移的關系曲線。其中試樣所受剪應力為墻體1、2、4、5所受X方向的應力平均值，豎向應力為墻體1與墻體4所受到的Y方向應力平均值。如圖2所示，素土與纖維土的應力應變曲線都具有相同的變化趨勢，剪應力都隨著剪切位移的增加而逐漸增加，沒有明顯的峰值強度，呈現出應變硬化型，這與試驗得出趨勢相同；在剪切初期素土與纖維土的強度曲線基本一致，隨著剪切位移的增加素土與纖維土的曲線開始不同。纖維土與素土的峰值強度分別為86 kPa與75 kPa，纖維土峰值強度為素土的1.15倍，纖維土與素土的殘余強度分別為 75 kPa與65 kPa，纖維土殘余強度為素土的1.15倍，其強度增加也與實際相符。以上結果可表明，該模型得出的結果與真實土體反映的規律趨勢一致，故可用來進行剪切過程中纖維與土體作用機理的研究。選取剪切過程中三個典型位移點(圖2)進行分析，分別位于剪切位移為2 mm處即峰值位移前(Ⅰ)、剪切位移為8 mm處即峰值位移處(Ⅱ)與剪切位移為12 mm處即峰值位移后(Ⅲ)。

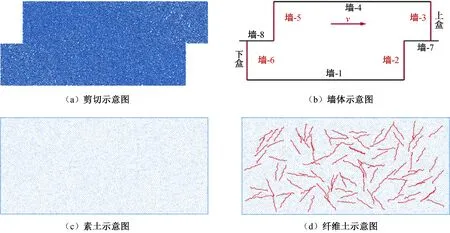
圖1 直剪試驗模型示意圖

表1 土體參數值

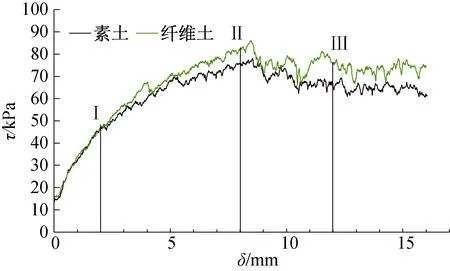
圖2 素土與纖維土剪應力與剪切位移關系曲線圖

1.3 顆粒運動特征

(1)單顆粒運動

如圖3所示，顆粒在t時刻時處于O點，經過Δt時間后處于O′點，則其位移矢量為ds，其X方向位移為dx，Y方向位移為dy，其轉角位dθ，規定以逆時針方向為正。

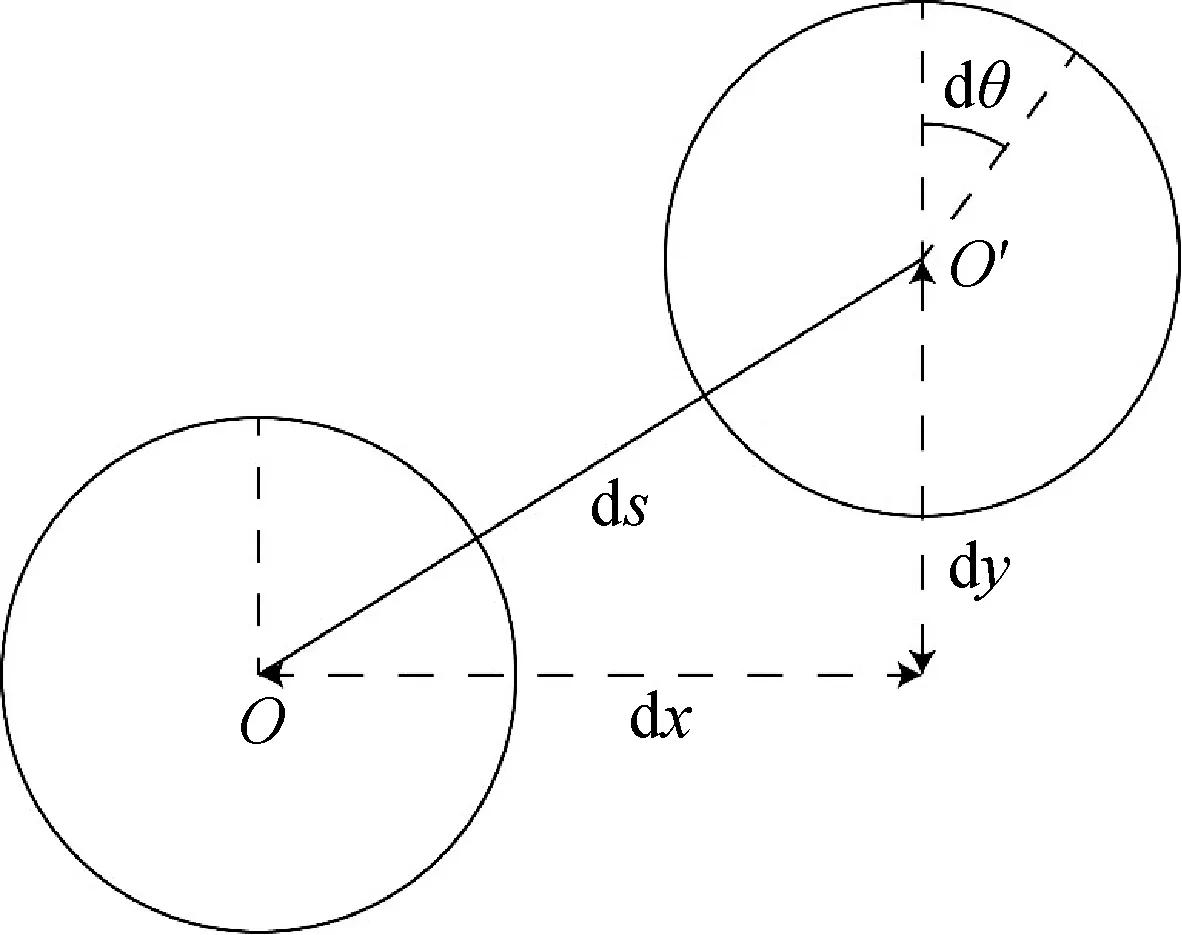
圖3 單顆粒運動位移轉角示意圖

(2)顆粒間接觸運動

如圖4所示，顆粒一與顆粒二半徑分別為r1、r2，在t時刻兩個顆粒接觸點上的法向量記為n，經過Δt時間后接觸點上的法向量記為n′，n與n′ 間的轉角記為dβ。兩顆粒的轉角分別為dθ1、dθ2。它們之間滿足

da=r1(dθ1-dβ)

(1)

db=r2(dθ2-dβ)

(2)

da與db分別為顆粒一與顆粒二轉動的弧長，其可分解為顆粒間的滑動dUs與轉動dUr，即

da=dUs+dUr

(3)

db=dUs-dUr

(4)

因此顆粒間的滑動與轉動分別為

(5)

(6)

該定義可較直觀地反映顆粒間的相互運動。因顆粒間接觸的滑動與轉動無方向選擇性[10]，故對其取絕對值進行分析。

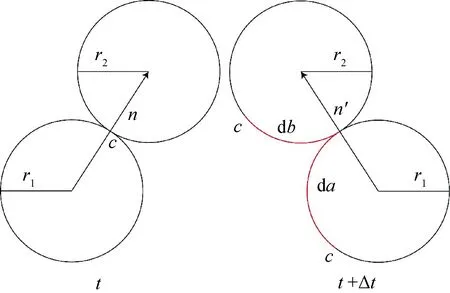
圖4 顆粒間運動位移轉角示意圖(據Yuan等[10]與陳慶[12])

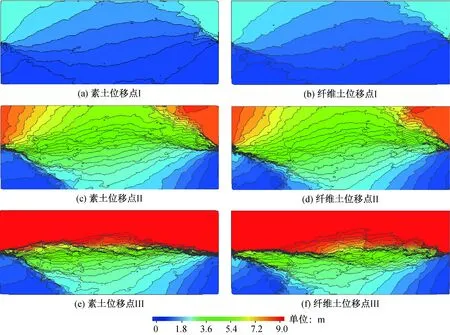
圖5 素土與纖維土顆粒位移大小在典型剪切位移點的等值線分布

2 顆粒運動特征

2.1 單顆粒運動特征

圖5展示了素土與纖維土隨著剪切的進行土體內部顆粒位移的等值線分布規律。從圖中可以看出，在剪切剛進行時素土與纖維土的位移規律基本一致，等值線均勻的分布在盒內，并且位移從上盒到下盒逐漸減小；隨著剪切的進行，素土與纖維土的等值線分布規律圖出現了一些差別，素土中等值線在中間部分較為密集，纖維土的等值線較為均勻地分布在上下盒中。隨著剪切的進一步進行，等值線已經集中分布在試樣的剪切部位，素土等值線集中區域較大，纖維土等值線集中區域較小。在上半盒集中區域外素土等值線分布范圍小且集中，纖維土等值線分布范圍大且均勻。從上面這些現象可以看出，在剪切剛進行時由于剪切位移較小此時纖維并未發揮作用素土與纖維土的位移基本一致，隨著剪切的進行纖維對土體的作用逐漸增強，致使上半部分與素土相比位移變小，下半部分與素土相比位移變大。當土體的剪切位移超過峰值位移后，素土的剪切帶較寬對剪切帶周圍土體的影響較弱，纖維土的剪切帶較細對剪切帶周圍土體的影響較強。為更加清晰地展示纖維土與素土的位移變化，本文把試樣從下到上分成了n份，求每份位移的平均值，再用素土每份的位移減去對應的纖維土的位移，得到圖6。通過圖6可以更加清晰的看出纖維土與素土的位移變化的趨勢，即：隨著剪切位移的增加纖維土與素土的位移差別也逐漸增加，在剪切帶周圍纖維土的位移更大，在上部纖維土的位移更小，纖維土表現出更大的整體性土體的位移更加均勻。

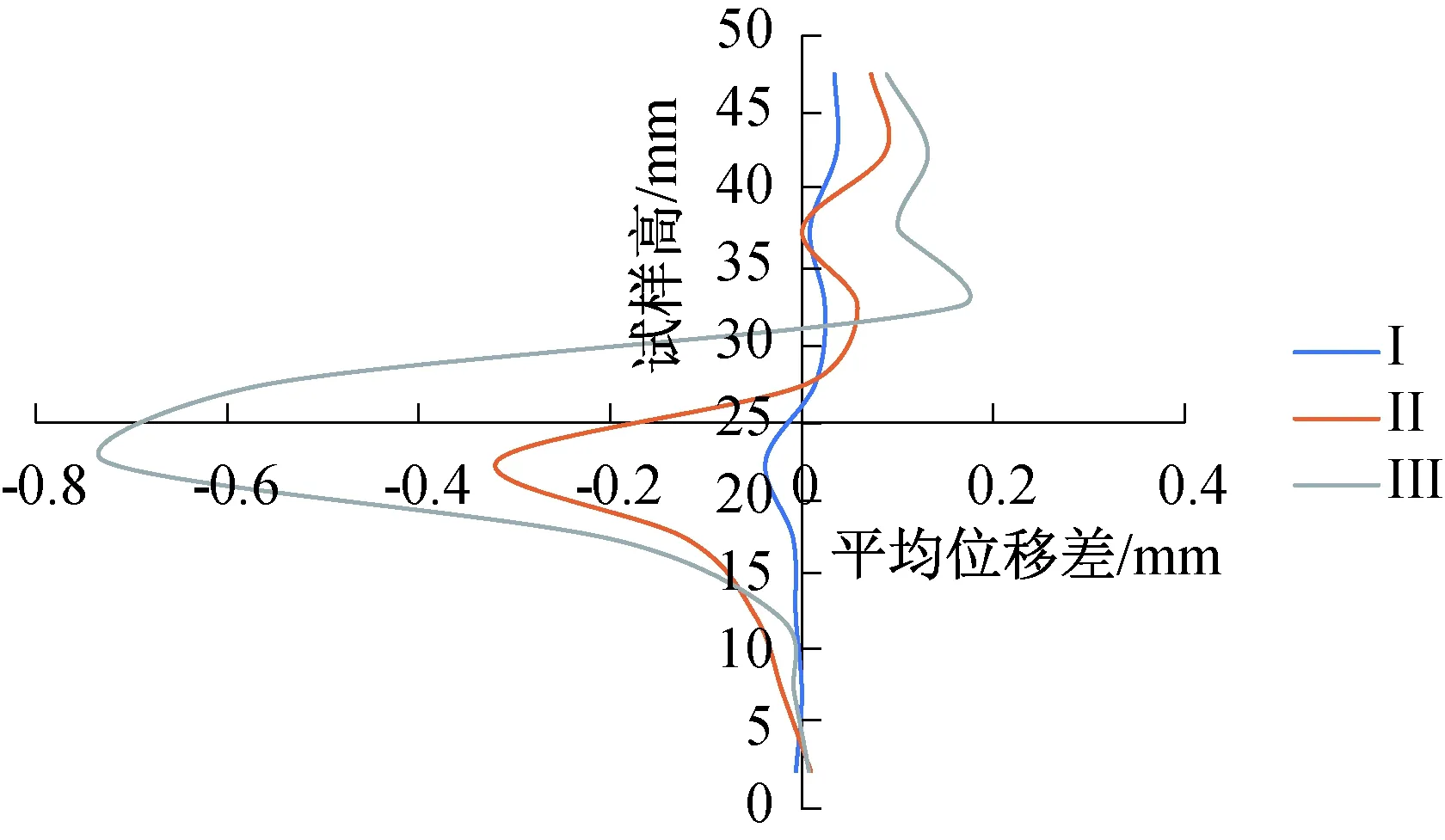
圖6 典型剪切點素土與纖維土位移差值圖

土體轉動的空間分布規律如圖7所示。在剪切剛開始時，素土與纖維土的轉動規律基本一致。當剪切位移達到峰值位移時，素土在土體開裂處有些許轉角，試樣中部沒有轉角；纖維土在裂開處存在轉角且范圍較大，在試樣中部存在些許轉角并以初步貫通試樣。當剪切位移超過峰值位移后，素土的貫通區域寬但周圍土體很少有大轉角的區域；纖維土貫通區窄，但周圍土體排列著一些大轉動區，并使纖維土的大轉角區域呈現出類似“魚骨”狀。我們更進一步將土體分為若干區域，分析土體每一區域的平均轉動列出圖8。通過圖8可以看出素土在剪切帶附近的轉角大于纖維土的轉角，在遠離剪切帶處纖維土的轉角與素土的轉角相差不大。通過對比圖7與圖8從中可以分析出在剪切帶內纖維土的轉角略小于素土的轉角，在剪切帶外纖維土在纖維處土體具有很大的轉角，遠離纖維處土體轉角很小。故纖維土的大轉角主要分布在剪切處與纖維處。

圖7 素土與纖維土顆粒轉動在典型剪切位移點的等值線分布

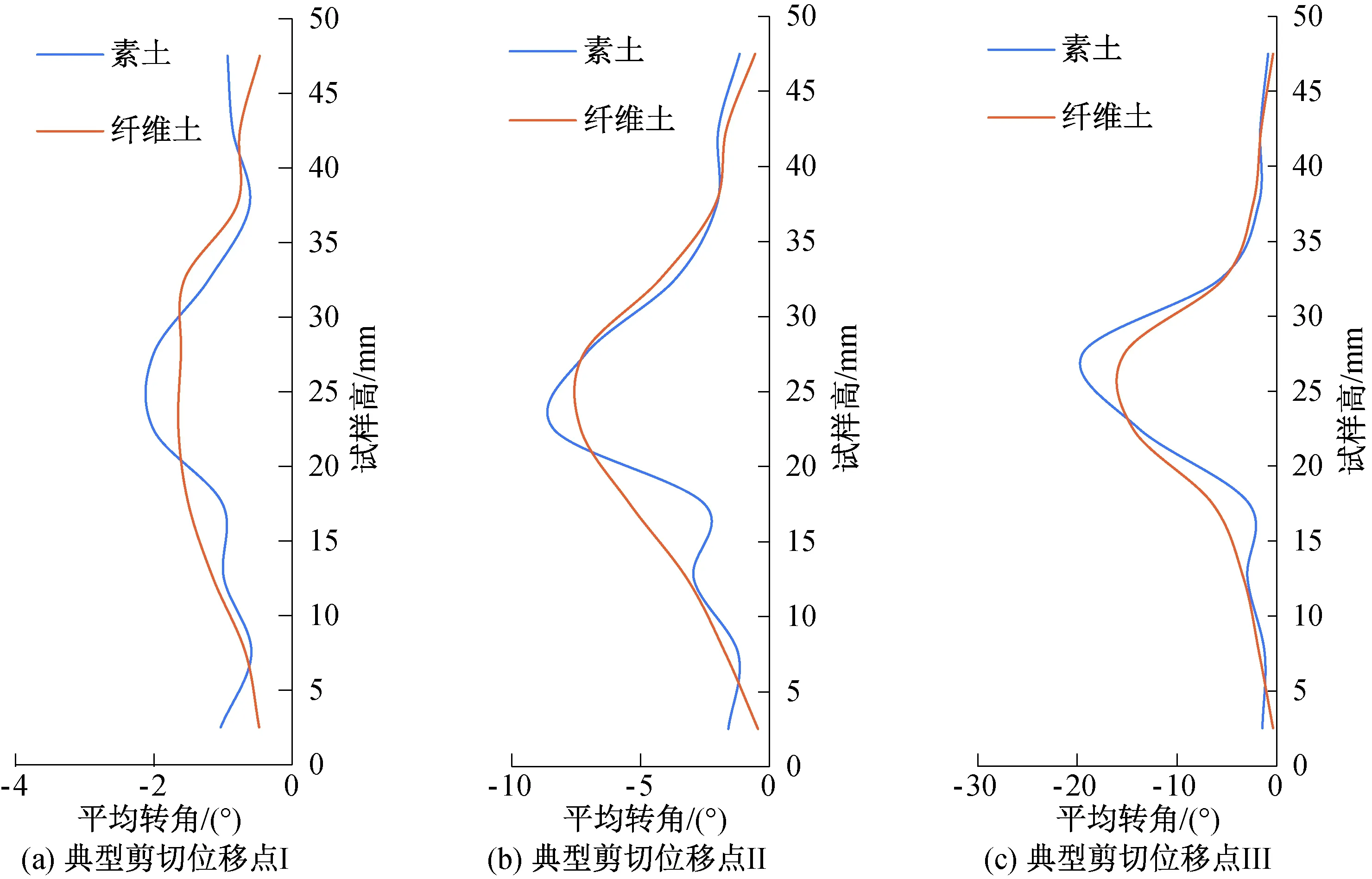
圖8 素土與纖維土平均顆粒轉動在典型剪切位移點的分布

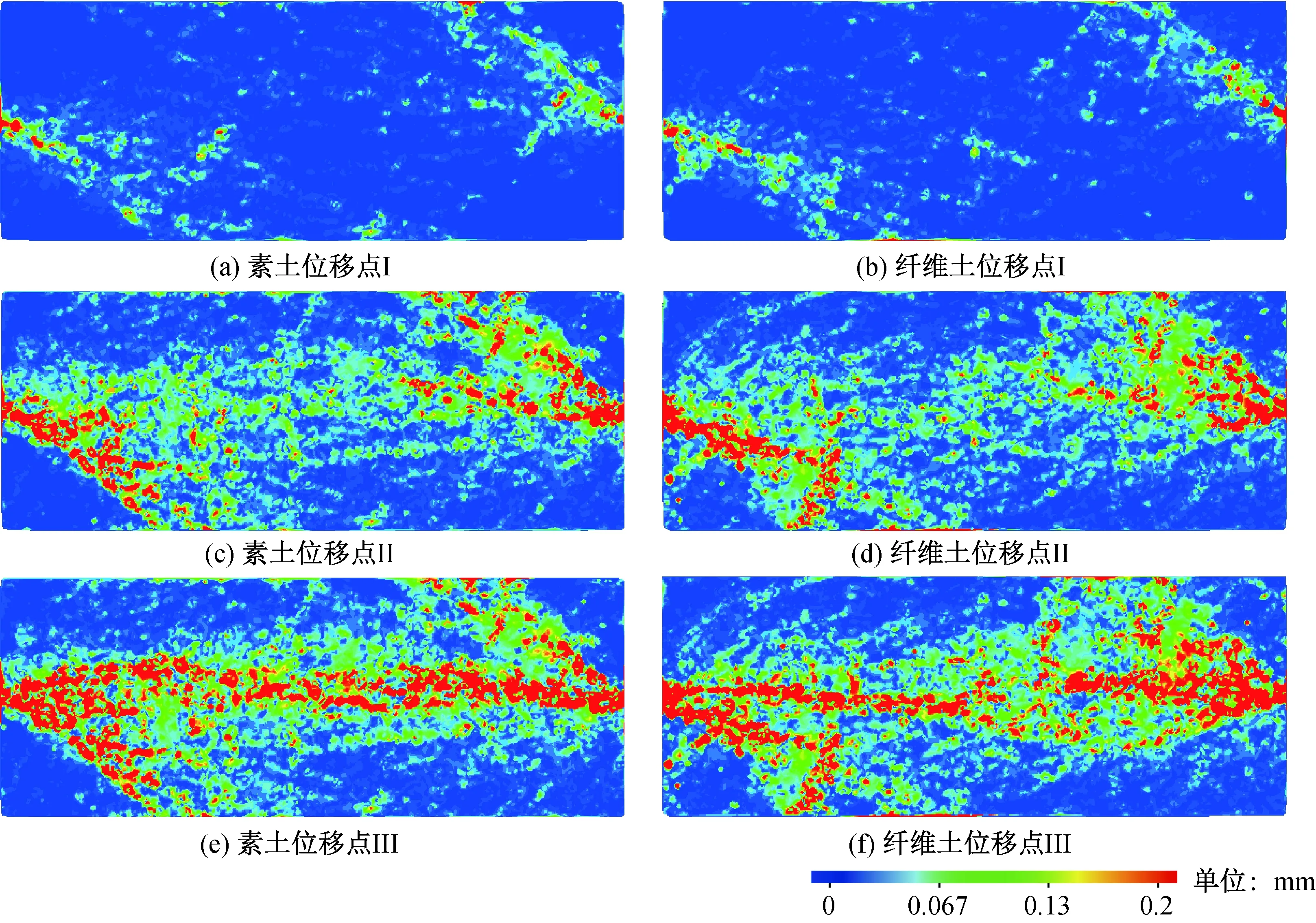
圖9 素土與纖維土相對滑動在典型剪切位移點云圖

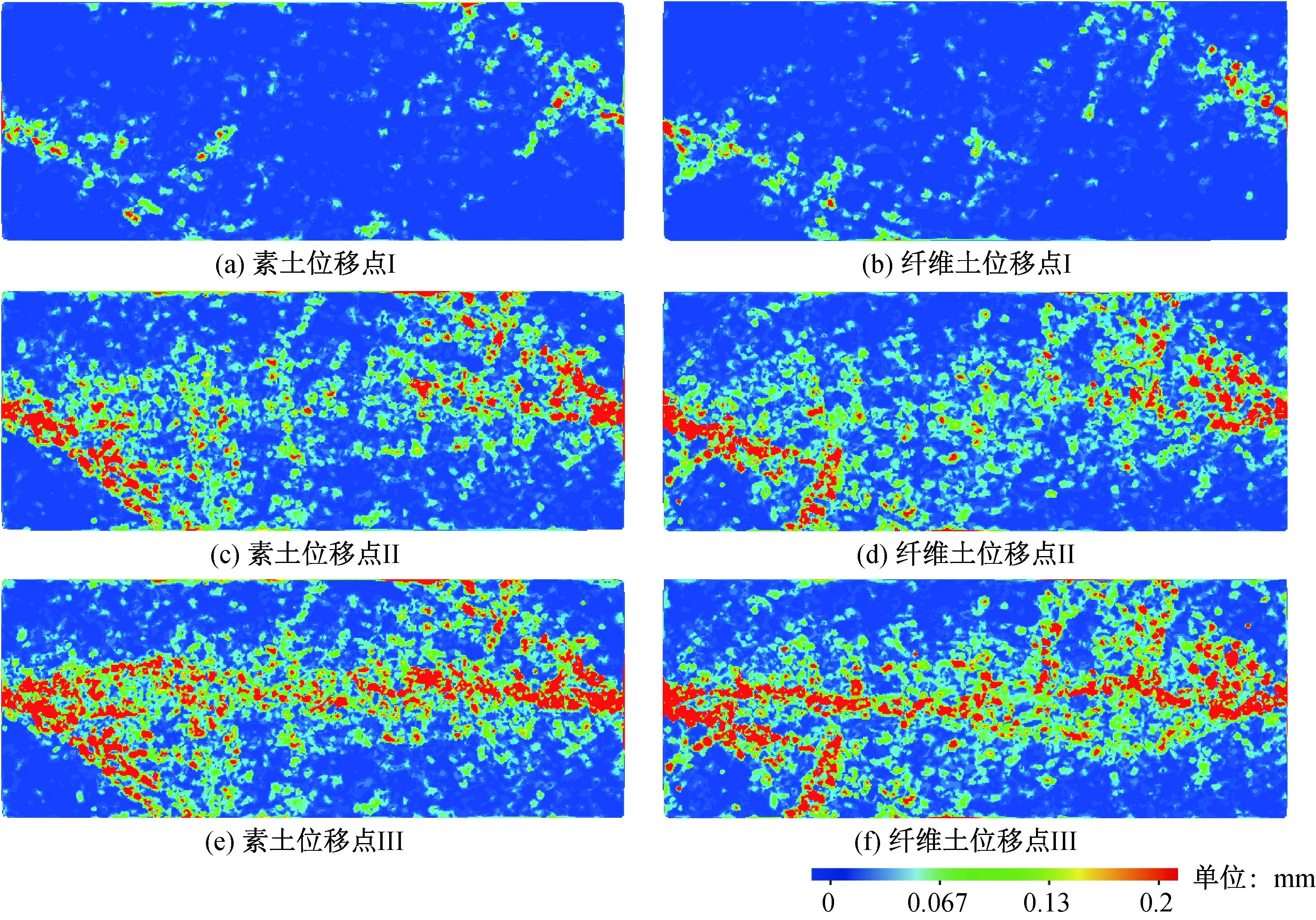
圖10 素土與纖維土相對轉動在典型剪切位移點云圖

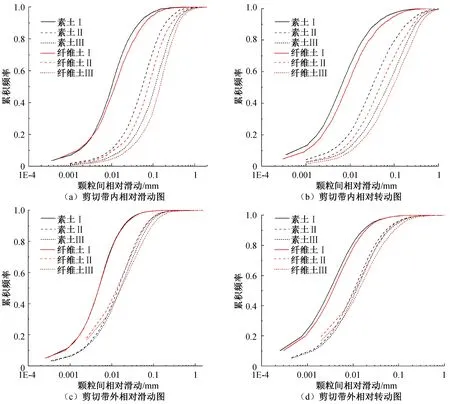
圖11 素土與纖維土在滑動帶內外的相對轉動與相對滑動的頻率分布圖

2.2 顆粒間運動特征

顆粒間運動特征能夠較為清晰地展示顆粒之間的相互運動，因此更能夠直觀地展示出剪切帶的大小。通過觀察圖9與圖10可以看出在峰值位移前，因為土體的開裂土體在左下角與右上角產生了滑動與轉動。當達到峰值位移時，素土顆粒間的滑動與轉動較為集中且范圍更大，纖維土的滑動與轉動范圍與素土相比較小。當剪切位移超過峰值位移后顆粒間的大滑動集中于剪切帶內，且形狀與剪切帶一致。據此估算出素土的剪切帶約為8 mm，纖維土的剪切帶約為5 mm。圖11為素土與纖維土在滑動帶內、外的相對轉動與相對滑動的頻率分布圖，可以看出隨著剪切的進行土體的相對轉動與相對滑動都相應地增大，剪切帶內纖維土的相對滑動與相對轉動都略大于素土，剪切帶外纖維土與素土的相對滑動與相對轉動基本一致，在I階段時剪切帶內外的相對滑動與相對轉動基本一致，隨著剪切的進行，當剪切到達II階段時剪切帶內的相對滑動與相對轉動大于剪切帶外的約1.2倍，當剪切到達III階段時剪切帶內的相對轉動與相對滑動大于剪切外的約10倍。

3 結論

1)剪切剛開始時素土與纖維土的位移等值線差別不大，隨著剪切的進行等值線逐漸向中間集中，素土等值線集中區域較寬，纖維土等值線集中區域較窄。纖維土在剪切部位位移較大，在上部位移較小，體現出了更大的整體性。

2)在峰值位移前，纖維土的大轉角區域較素土大。峰值位移后，素土的大轉角區域較粗，周圍土體基本不存在大轉角區域；纖維土的大轉角區域較細，周圍土體條狀分布著大轉角區域。纖維土的大轉角主要分布在剪切處與纖維處。

3)素土的剪切帶較纖維土的剪切帶大。剪切帶內纖維土的相對滑動與相對轉動都略大于素土。剪切帶外纖維土與素土的相對滑動與相對轉動相差不大。不論剪切帶內外土體的相對滑動與相對轉動都隨著剪切發展而增加。