基于熱傳導模型的熱防護服設計

摘要：消防員等高溫環境工作者都會配備熱防護服，保障高溫作業人員在接近熱源時免受傷害。熱防護服通常由三層織物材料構成，服裝與人體皮膚之間還有一定的空隙，可認為人體與外環境之間存在四層隔離。本文建立四層隔離和皮膚層之間的熱傳導模型，用有限差分法求解熱傳導的偏微分方程，對熱防護服進行設計，確定熱防護服各層的厚度范圍。最后從安全和舒適兩個目標出發建立雙目標優化模型并求解，得到熱防護服的各層最優厚度。

Abstract： Firemen and other high-temperature environmental workers should be equipped with protective clothing against heat to avoid injuries while approaching heat sources. Protective clothing against heat is usually composed of three layers of fabric material， and the air between clothing and human skin can be regarded as the fourth layer of isolation between external environment and human body. In this paper， the heat conduction model between the four layers of insulation and human body is established. The partial differential equation of heat conduction is solved by the finite difference method， and the thickness range of each layer of thermal protective clothing is designed. Finally， based on the safety and comfort objectives， a double object optimization model is established and solved to obtain the optimal thickness of each layer of thermal protective clothing.

關鍵詞：熱防護服;熱傳導;有限差分法

Key words： protective clothing against heat;heat conduction;finite difference method

中圖分類號：TS941.2???????????????????????????????????? 文獻標識碼：A????????????????????????????????? 文章編號：1006-4311（2020）28-0194-02

1? 問題簡述

1.1 背景? 消防員等高溫環境工作人員都會配備具有防火、隔熱、阻燃等特性的專用工作服，穿上這種服裝，高溫作業人員即使接近熱源，也不會受到酷熱、火焰、蒸汽等的侵害。高溫作業專用服裝一般由三層織物材料構成，當物質之間存在溫度差時，就會出現熱量傳遞的現象。

1.2 需要解決的問題? 利用數學模型解決以下問題：①對環境溫度為75℃、防護服II層厚度為6mm、IV層厚度為5mm、工作時間為90分鐘的情形開展實驗，記錄假人皮膚外側溫度。根據環境溫度和假人皮膚外側溫度求中間各層的溫度分布。②當環境溫度為65℃、IV層的厚度為5.5mm時，確定II層的最優厚度，確保工作60分鐘時，假人皮膚外側溫度不超過47℃，且超過44℃的時間不超過5分鐘。③當環境溫度為80℃時，確定II層和IV層的最優厚度，確保工作30分鐘時，假人皮膚外側溫度不超過47℃，且超過44℃的時間不超過5分鐘。

2? 溫度的分布

2.1 熱傳導過程? 首先將人體形狀視作圓柱體。假人體內溫度恒定37℃，但是假人皮膚外側的溫度是變化的，所以人體并不能看作一種物質構成的整體，而應該包含皮膚層和內部兩種結構。

本題中熱量在空間上的傳導為一維形式，如下式：

（1）

熱防護服的熱傳導過程如圖1所示，最右側的人體實際上是人體皮膚外側，計算時使用實驗記錄的人體皮膚外側溫度作為右邊界條件。圖中I、II、III、IV四層各自均符合熱傳導方程式，對空間和時間進行離散處理，形成時間空間網格，用有限差分的方法解熱傳導微分方程。

根據熱傳導情況和對人體的假設，可以列出一個帶有求偏導數的方程，在有初始條件和邊界條件限制時，此方程存在唯一穩定的解。初始條件即初始0時刻的時候，各個位置的函數值。邊界條件即在位置開始和結束兩個位置上的各個時刻的函數值，或者函數值的導數的值，本題目分了4個偏微分方程，因而在每個邊界都要有邊界條件。用數值法求解的時候，需要把方程和邊界條件全部進行差分。

由傳熱學相關研究可得邊界Ⅰ與外界環境之間的換熱微分方程得到Ⅰ層與外界環境的第三類邊界條件為[1]：

（2）

其中h1為空氣層對流換熱系數，取值20。

為保證邊界時溫度的連續性，Ⅰ層與Ⅱ層之間的連續型邊界條件如式（3）和式（4），其它各層之間的邊界條件也類似。

（3）

（4）

Ⅳ層與人體內的溫度邊界為人體皮膚層，則在人體內外側邊界的邊界條件假設為換熱微分方程：

（5）

其中h2為皮膚層的對流換熱系數，可以通過給出的皮膚外側溫度來算出。

總的熱傳導微分方程模型為：

（6）

其中ui表示各層的溫度，li表示第i層的厚度，ti表示時間節點劃分，tw就是最后一個時間節點。已知初始條件為u（x，0）=37，再以四層材料邊緣處的溫度為邊界條件，理論上即可求解微分方程組。

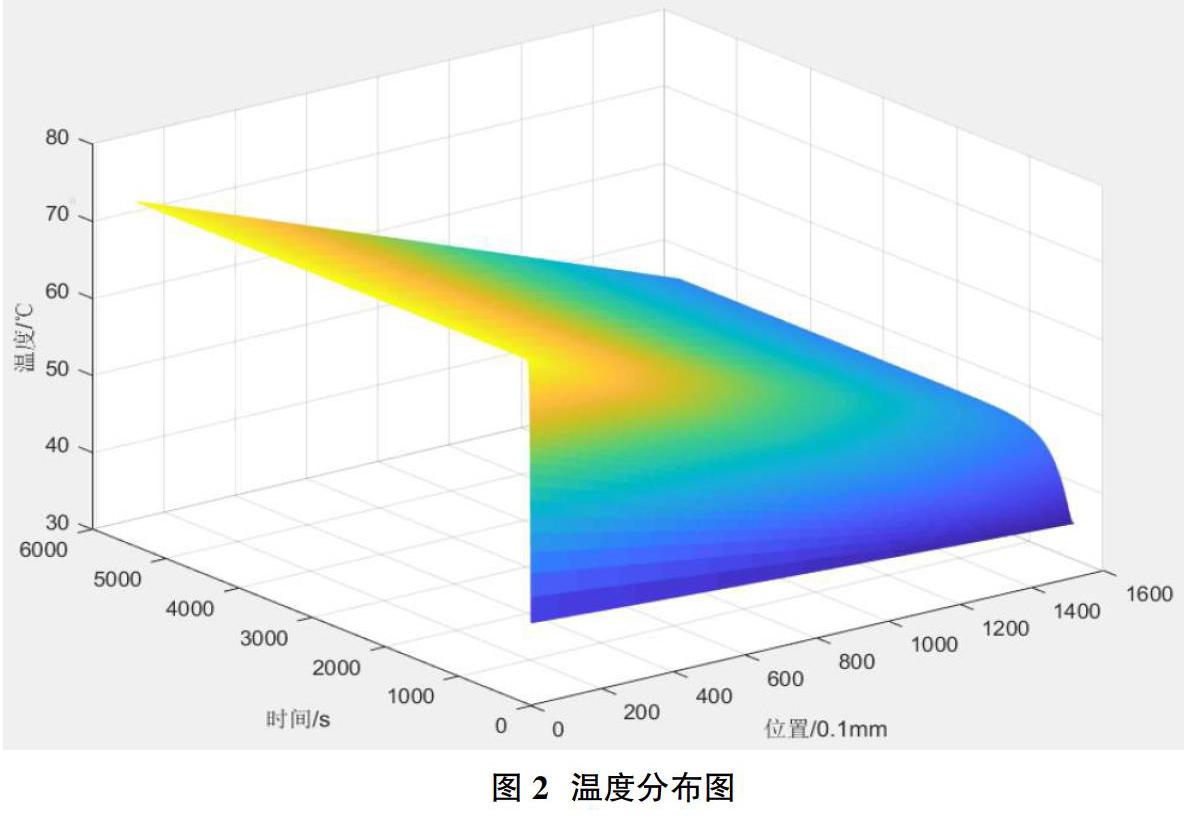
2.2 求解熱傳導模型? 利用Matlab軟件求解，可以得到時間空間網格中每個結點的溫度，即溫度的時間和空間分布，繪制溫度分布圖。

如圖2所示，多層材料在從室溫條件下進入高溫工作環境后不同厚度位置處的溫度隨時間變化情況已給出。其中越靠近熱源地方初始時刻溫度上升的越快，在接近皮膚處地方由于皮膚初始溫度為37℃高于初始時刻的內層材料溫度，因此在初始時刻溫度上升時呈現出兩邊快，中間延后的情況。再考慮經過一段較長工作時間90分鐘后，各層材料厚度基本達到穩態，穩態時越靠近外界環境處的溫度越高。

3? 材料層的最優厚度

當環境溫度低于75℃時，對上述防護服的規格要求就會有所降低，這種情況下仍然使用高規格的防護服是一種材料的浪費，同時也會令穿著者感到笨重。如果要節約成本，提高使用舒適感，就要針對不同外界環境的溫度設置不同厚度的材料層。某層材料變薄，對熱量的阻隔作用就會變差，皮膚外側收到的保護削弱，升溫越快。而外界環境溫度的降低則減緩皮膚外側升溫，兩個作用效果相反的因素結合，當一個因素確定時，應該有一個與之對應的最佳搭配，恰好能物盡其用。

由于約束條件中的直接研究對象是Ⅳ層右側、皮膚表面的溫度，這里的溫度是會變化的，而人體內體溫是恒定的37℃，這里的溫度不連續說明在皮膚表面與人體內部存在著一個皮膚層。改變模型中的環境溫度u外為65℃，Ⅳ層厚度為5.5mm，建立最優化模型。

已知Ⅱ層的厚度范圍，利用二分法尋找滿足約束條件的最優厚度。首先在Ⅱ層厚度區間取中值，驗證該中值是否能使假人皮膚外側溫度不超過47℃，且超過44℃的時間不超過5分鐘。若符合這個條件，在數值偏小的半區間繼續取中值檢驗，若不符合，在數值偏大的半區間繼續取中值檢驗，重復這個過程，最終就會得到一個具有一定精度的最優厚度。二分法尋找的過程由Matlab編程實現，最后得到第二層最優厚度為9mm。

4? 材料層和空氣層的最優厚度

當材料層Ⅱ和空氣層Ⅳ的厚度都未知時，用雙目標優化的思想求解模型，有兩個未知厚度層，且外界環境溫度發生了改變（u外為80℃）。優化的目標依然是要既滿足約束條件，又輕便靈活，節約材料。

約束條件是工作30分鐘時，假人皮膚外側溫度不超過47℃，且超過44℃的時間不超過5分鐘。經計算，L2+L4的最小值為14.2。

為使服裝滿足約束條件，有良好的隔熱性能，Ⅱ層材料厚度設計應盡量大，Ⅳ層厚度應盡量小;為使服裝輕便舒適，降低成本，Ⅱ層材料厚度應盡量小，Ⅳ層厚度應盡可能大，且Ⅳ是空氣層，不需要材料，而Ⅱ層是織物，需要材料，為了節省成本，Ⅱ層應盡可能薄。將雙目標統合為同一目標進行有效分析，最優厚度的評價標準y

y=s+c（7）

式中s表示安全性，c表示舒適性。

根據各層材料的參數，熱傳導率越大越安全，密度越小越舒適的基本規則，對Ⅱ、Ⅳ兩層進行安全和舒適評估打分，最后得到雙目標優化模型的最優解為：Ⅱ層厚度9.8mm，Ⅳ層厚度4.4mm。

5? 總結

多層熱防護服設計的重點是確定各層材料厚度，使熱防護服既能滿足防護要求，又盡量輕便省料，難點在對熱防護效果的分析上。本文以四層熱防護服為例，根據傳熱原理建立熱傳導微分方程組。經典的導熱微分方程在本問題中的形式比較復雜，計算困難，使用有限差分法求解偏微分方程，容易通過計算機軟件計算，得到較為精確的數值解。

參考文獻：

[1]張興中，黃文，劉慶國.傳熱學[M].北京：國防工業出版社，2011.

[2]張奕.傳熱學[M].南京：東南大學出版社，2004.

[3]潘斌.熱防護服裝熱傳遞數學建模及參數決定反問題[D].杭州：浙江理工大學，2017.

[4]許維珍.熱傳導中應用數學建模的探討[J].赤峰學院學報（自然科學版），2008（07）：26-29.

[5]盧天健，徐峰.皮膚傳熱的雙相位滯后模型[J].西安交通大學學報，2009，43（05）：1-7.

作者簡介：白曉萌（1998-），女，河南鄭州人，本科，研究方向為數學建模。