基于陀螺儀轉角傳感器的動態信號測量及物理參數時域識別

周云 曾雅麗思 趙瑜 易偉建

摘? ?要：針對結構識別算法應用于實際工程時，結構的轉角信息難于準確測量及轉角自由度通常容易被忽略的問題，本文研究了使用陀螺儀轉角傳感器測量動態信號的方法及響應信息不完備條件下的結構物理參數識別.首先，針對結構轉動響應信息測量困難這一問題，提出采用商業級的微機電系統（MEMS）陀螺儀傳感器測量角度和角速度響應，并基于最小二乘遞推算法對結構物理參數識別方法進行了理論公式推導.然后以一座4層框架結構為算例進行分析，設置由廣義逆方法重構轉角和采用轉角真實值兩種工況，并對結構物理參數進行識別，從而驗證了理論推導的正確性.同時，對兩種工況下所識別的物理參數進行比較，結果表明重構轉動響應時物理參數識別的效果不夠理想，故考慮測量轉動響應.先對MEMS陀螺儀傳感器在受到沖擊振動下的動態精度進行了試驗驗證，在結構的初位移小于10 mm時，動態角度測量的精度為0.1°.在此基礎上，通過一個3層2跨的鋼框架模型的動力試驗實測數據和分析結果，驗證了使用MEMS陀螺儀傳感器直接測量轉動響應相比于重構轉動響應對彎剪型結構進行剛度參數時域識別的效果更好.

關鍵詞：陀螺儀;動轉角;參數識別;時域;框架結構

中圖分類號：TU317? ? ? ? ? ? ? ? ? ? ? ? 文獻標志碼：A

文章編號：1674—2974（2020）09—0010—13

Abstract：When the structure identification algorithm was applied to practical engineering， the structure angle information was difficult to accurately measure and the degree of freedom of rotation was often neglected. The method of measuring dynamic signals with gyroscope sensor and the identification of structural physical parameters under the condition of incomplete output information were studied in this paper. Firstly， a commercial Micro Electro Mechanical Systems （MEMS） gyroscope sensor was proposed to measure the angular velocity and angle responses， and the theoretical formulas of structural physical parameters identification method based on the least square recursive method were deduced. Then， taking a four-story frame structure as an example for analysis， two working conditions that the rotation angle reconstructed by the generalized inverse method and the adoption of the true value of rotation angle were set up， and the physical parameters was identified. The correctness of the theoretical derivation was verified. The results of physical parameters identified under two working conditions were compared， which reflected that the effect of physical parameter identification was not very ideal when the angular response was reconstructed， so we can consider measuring the rotational responses. The dynamic accuracy of MEMS gyroscope sensor under impact vibration was verified by experiments firstly. The results demonstrated that the accuracy of dynamic angle measurement was 0.1° when the initial displacement of the structure was less than 10 mm. On this basis， the measured dynamic test data and analysis results of a three-story and two-span steel frame model verified that using MEMS gyroscope sensor to directly measure the rotational response was better than using reconstructed rotational response for the time domain identification of stiffness parameters for the bending-shear structure.

Key words：gyroscope;angle of rotation;parameter identification;timedomain;frame structure

系統識別方法始于20世紀70年代，引入土木工程領域已有近40余年的發展歷史[1].該方法是工程結構損傷診斷和狀態評估的重要手段，它可以從建筑物動力響應中識別出結構的當前狀態.結構的性態通常用結構模態參數（主要為自振頻率和振型）和結構物理參數（主要為剛度參數）來描述. 結構物理參數的變化相比模態參數的變化更為直觀地反映了結構狀態的改變[2]. 進行結構物理參數識別的方法，主要分為頻域識別和時域識別兩種，與頻域識別方法相比，時域識別更加直接，實測的時程數據中的結構信息更加豐富，且增加時程響應采樣點數可以有效增加時域識別方程的個數[3]. 目前制約時域識別應用于實際工程中的一個主要原因是結構響應信息不完備，通常時域方程中主要使用位移類信息，轉角類信息很難測試得到，往往只能測量結構的一個狀態量，加速度、速度或位移響應的一種，而且轉角信息難以準確測量.如何在測量信息有限的情況下識別參數以及如何進行信息不完備情況下的識別問題是研究重點之一[4].

為了解決這些問題，眾多學者展開了相關研究.擴展卡爾曼濾波[5]方法可以求解響應信息不完備下的結構參數識別問題，但結構參數的識別精度低，甚至會出現參數發散現象.傳統方法主要通過重構技術解決時域識別時測量信息的不完備問題.平動信息不完備的處理方法如下：Li等[6]在獲得系統的位移響應后，通過采用微分算子變換方法求得速度與加速度響應，完成系統的參數識別. 李國強等[2]采用積分算子變換方法，實現了在無需初速度信息的情況下，由加速度響應重建位移、速度響應.轉動信息的計算問題主要采用靜力凝聚法[2]和廣義逆方法[7]通過水平位移測量值重構轉動信息，前者需要預先知道結構的參數信息，而后者不需要，但是兩種方法計算效果近似，因此廣義逆方法更具適用性. 此外，趙昕等[8]采用一組正交基函數對梁式構件的平動反應曲線進行擬合，從而獲得其轉角響應信息.

關于測量動態旋轉角度的研究不多，主要是因為轉動響應的最大振幅通常在毫弧度范圍以內，所以要求儀器必須非常靈敏，而且需對測量的運動以外的其他運動非常不敏感[9]. 通過文獻調研發現，Ewins等[10]在文獻中對轉角自由度間接測量方法進行了詳細的分類介紹.包括采用附加T模塊法[11]、激光多普勒測振儀[12]、激光位移計[13]等測量轉角，但這些測量方法和設備過于復雜，難以運用于自由度較多的情況. Lee等[14]采用商用相機和低成本的幀捕獲器，利用事先標定參數的圖像處理技術，測量了五層試驗塔在激振器下的角度響應.然而，攝像機的方法需要額外的計算圖像處理，如像素掃描、目標識別和輪廓定義，實際應用并不方便. 也有學者嘗試采用應變推算轉角，Xia等[15]通過在廣州塔上安裝振動應變儀，利用實時監測的應變數據計算彎曲梁型結構頂部的傾斜角度，Dimsdale[9]采用在桿件兩端粘貼應變片的方式間接計算桿件兩端的彎曲轉角，該方法的應用前提是與其他桿件的連接方式不影響桿件的相對轉動.測量轉角自由度的傳感器技術遠不如測量位移自由度的傳感器成熟，目前采用較多的是傾角儀和陀螺儀，Hou等[16]利用MEMS傾角儀監測鋼筋混凝土柱在地震荷載作用下的結構旋轉角，該傳感器對被測物體的振動頻率非常敏感，僅適用于1 Hz以內的外激勵頻率.傾角儀適合低頻的振動，而陀螺儀在高頻振動下的性能更為穩定，是測量動態角度的理想傳感器.

由于轉角響應難以獲得，目前結構識別算法的研究主要集中于剪切型結構和桁架結構[17-18]，而以彎剪變形為主的結構研究較少.彎剪型結構在正問題分析中通常利用靜力凝聚的方法縮聚掉轉角自由度，在反問題求解過程中，主要利用平動響應重構轉動響應.目前關于如何通過直接測量得到動態角度信息的研究十分有限，測量轉角自由度的傳感器價格也普遍較高，不適合大量應用于工程結構中.在時域識別方面，傳統算法在重構狀態信息以及廣義逆求轉角時，計算模型所使用的方程式存在對沖效應，需要應用超定方程組修正結果，方法過于復雜且精度不能完全滿足要求.因此本文以一座4層框架結構為例，在對該結構進行轉動信息重構的前提下，基于最小二乘遞推算法由結構的平動響應數據在時域內識別了結構的物理參數.對比運用轉動響應真實值的情形下所識別的物理參數，研究使用轉角重構值對結構物理參數時域識別的影響.為獲得準確的轉角測量值，本文利用MEMS陀螺儀傳感器，依據由平動響應信息擬合轉動響應的原理，對其在受到沖擊振動下的動態精度進行了試驗驗證. 在此基礎上，通過一個3層2跨的鋼框架模型的動力試驗，比較了采用廣義逆方法重構轉角和直接測量轉角兩種情況下，阻尼參數和剛度參數的識別效果.

1? ?MEMS陀螺儀傳感器簡介

陀螺儀是一種可以用來測量被測物體相對于慣性空間的角速度和角位移的慣性器件.其基本的工作原理為，高速旋轉剛體的旋轉軸在不受外力影響時，其所指方向不改變. 陀螺儀在載體姿態測量方面具有穩定性好、精度高、對環境的適應能力極強等諸多優點，被廣泛應用于航空飛行器姿態測量、軍事軌跡測量、車輛駕駛控制、數碼產品如相機防抖、手機體感操作功能等領域.

MEMS陀螺儀使用現代的微機電技術，具有體積小、質量輕、成本低、集成度高和精度較高的特點，具有良好的應用前景[19].本文的研究選用的是商業級的MEMS陀螺儀傳感器，深圳維特智能科技的HWT901B姿態測量傳感器，它集成了高精度的陀螺儀、加速度計、地磁場傳感器等模塊. MEMS陀螺儀傳感器通過采集加速度、角速度以及磁場信號的原始數據，使用高性能的微處理器與卡爾曼動態濾波算法，通過四元數方法解算得到圍繞X、Y、Z軸旋轉的俯仰角、偏航角和翻滾角. 因此，陀螺儀傳感器實際采集的是角速度響應，通過解算才能獲得角位移.HWT901B陀螺儀傳感器的性能參數如表1所示，其采集數據后，通過TTL電平串口進行數據傳輸，支持串口數字接口. 考慮到實際測量時距離較遠，研究團隊對其進行改造加入了HC-12無線收發傳輸串口通訊模塊，整套動態角度測量系統的連接方法如圖1所示.

2? ?基于轉角擬合的角度測量精度校驗

MEMS陀螺儀傳感器體積微小，內部含有多個運動單元，因此其性能對工作環境變化較為敏感.測量過程中的外界沖擊振動，環境干擾和自身漂移率都會影響陀螺儀的精度.目前，可通過提高微加工工藝消除尺寸偏差[20]、合理設計優化陀螺儀結構降低耦合誤差[21]、建立相應誤差模型進行對準[22]、采用數字信號處理技術減小隨機噪聲的影響[23]等方法來有效提高其精度，HWT901B正是采用卡爾曼動態濾波算法減少了其漂移誤差.考慮到動力試驗時，結構將產生高頻的往復振動，有必要對MEMS陀螺儀傳感器在受到外界沖擊振動下的動態精度進行校驗，一般采用陀螺測試轉臺來檢驗和評定陀螺儀性能，轉臺為精密測試設備，一般土木工程應用很少，考慮購買轉臺或對陀螺儀的精度進行檢測的送檢價格都過高，受實驗條件所限制，故采用了一種角度擬合方法[8]對MEMS陀螺儀傳感器的精度進行了驗證，通過對激光位移計實測的結構平動響應曲線擬合得到結構的轉動響應曲線.

如圖2所示的等截面梁單元，它聯結著兩個節點，一般不考慮軸向變形的影響，則該單元在平面內有4個自由度，包含2個平動自由度和2個轉動自由度.設有如圖3所示的受到脈沖激勵F，跨度為L的歐拉-伯努利梁，其撓度曲線上橫坐標為x的任一點的縱坐標為y，已知t時刻該梁上n個測點的平動反應測量值為

在有限單元法中，梁單元變形曲線為三次多項式，對于荷載作用下的歐拉梁，應當取不低于三次的多項式擬合梁的撓曲線.為求解三次多項式中的4個參數，應至少在梁上布置4個測點.

根據以上方程可知，只要通過激光位移計測試得到t時刻4個測點的位移y1、y2、y3、y4，基于梁單元變形曲線為三次多項式的假定，且已知4個測點的位置x1、x2、x3、x4，可以擬合得到梁在t時刻的撓曲線方程（1），求解出a1、a2、a3，將其代入式（2）可求得梁在t時刻的轉角反應，即可計算出t時刻橫坐標為xk處的轉角θ.

3? ?基于最小二乘遞推算法的結構物理參數時域識別

框架結構是由梁、柱構件組成的結構，可根據橫梁與柱的線剛度比值劃分為剪切型框架和一般框架結構.若線剛度比值大于5，則在結構分析中，可假定橫梁剛度無窮大，忽略梁的變形，視為剪切型結構[24]. 若框架梁柱的線剛度比值較小，則為一般框架結構.剪切型框架的參數識別已經比較成熟，本文研究對象為一般框架結構，在水平荷載作用下，其框架節點將發生轉動，因此需要考慮框架節點轉動的影響.

如圖4（a）所示的完整自由度模型一，對于鋼框架結構的梁柱連接節點，節點的軸向變形和剪切變形與它的轉動變形相比，可以忽略不計，因此框架結構計算模型采用梁單元的剛度矩陣為4 × 4階矩陣.對于單跨框架結構，由于結構對稱，左右兩側的轉動響應一致，可將模型一簡化為如圖4（b）所示的含N個平動自由度和N個轉動自由度的模型二. 對于多跨框架結構，同一層梁柱節點的轉角響應并不完全相同，根據實際情況，可將模型一簡化為如圖4（c）所示的含N個平動自由度和2 N個轉動自由度的模型三.

在外力f（t）作用下，對于需要考慮節點轉動影響的框架結構，動力平衡方程為

上述論述表明：利用系統的輸入、輸出響應信息可以得到結構的物理參數估計值.

3.1? ?無轉角測量值的求解——結構的轉角信息重構

以相對簡單的單跨框架結構為例說明，在沒有任何實測的轉動信息的基礎上，為了進行式（11）的計算，可采用廣義逆理論由水平位移測量值計算轉角，計算模型選取模型二.

由于該式中的Kφx 和Kφφ包含有待求參數，因此無法直接用來計算轉角響應. 陳雋[7]在文獻中給出了廣義逆方法計算轉角的公式：

由平動信息重構角度、角速度、角加速度信息后，可進行結構的參數識別.

3.2? ?有轉角測量值的求解

對于可以直接測量轉角值的框架結構，同樣以模型二為例說明，選取的待識別參數為各層的層抗彎剛度（EI）i和各層的阻尼參數b（EI）i. 根據前述理論介紹，可構造如式（10）所示的方程，第i層和第i+1層的參數識別方程如下式：

由式（19）可知，已知框架結構的各層層高、質量矩陣、所受外激勵以及各節點的平動、轉動時程響應，進而建立參數識別標準方程進行最小二乘遞推法參數識別，即可求得結構的物理參數.有轉角測量值即可省去采用廣義逆方法重構轉角信息的過程，更為方便.

4? ?算例分析

以一個4層彎剪型框架結構為例，在結構左側頂點水平施加一個大小為100 N的脈沖力F，采樣頻率設為200 Hz，共采集12 000個數據點. 計算模型如圖5所示，假設參數如表2所示.采用Newmark-β時程分析方法進行正問題計算得到結構的動力響應.動力方程中采用與剛度相關的比例阻尼矩陣和協調質量矩陣.采用忽略軸向變形和剪切變形的4×4階的桿系單元矩陣，組裝成16×16階的總剛度矩陣.模型共16個自由度，由于結構完全對稱，可簡化為含4個平動自由度和4個轉動自由度的框架模型，則總剛度矩陣變為8×8階的矩陣. 為了驗證算法的抗噪性能，在結構響應分析中分別加入1%、5%的白噪聲，加入白噪聲的水平由結構響應的均方根值和噪聲均方根值的百分比確定.接著使用最小二乘遞推算法對1～4層的層間抗彎剛度K1、K2、K3、K4和各層的剛度阻尼參數C1、C2、C3、C4進行識別.

根據實際觀測輸出信息，設置通過廣義逆方法重構轉角的工況1和采用轉角真實值的工況2. 其中輸出的加速度響應和角度、角速度響應都采用真實值.

工況1：采用Newmark-β積分法計算結構上4個平動自由度的加速度響應，對加速度響應進行傅里葉變換，將信號從時域轉換到頻域，再通過將時域內的積分轉換為頻域計算，在頻域內進行運算過后再通過傅里葉逆變換將信號從頻域還原到時域，并取其實部就可以得到信號在時域的速度和位移響應[25]，采用3.1節所述廣義逆方法，根據式（15）（17）和（18）由位移響應重構角度、角速度、角加速度響應.

工況2：基于圖5的計算模型，采用Newmark-β積分法計算結構上4個平動自由度的加速度響應，4個轉動自由度的角度、角速度響應.然后，同工況1的方法由頻域積分法獲得速度和位移響應.對角速度響應利用向前差分的數值微分法重構角加速度的響應，初始角速度為0.

獲得完備的輸入和輸出響應信息后，假設結構的待識別參數初值，將以上數據和結構的已知參數代入公式（19）構造結構參數識別方程，根據式（11）運用最小二乘遞推算法可求出結構物理參數的識別值，參數識別結果列入表3，圖6為不考慮噪聲下，工況1和工況2識別結構物理參數的收斂過程.

比較工況1和工況2在無噪聲時的結構參數識別結果，可以發現工況1重構轉角響應時剛度參數識別的最大誤差為13.04%;而工況2采用角度和角速度響應真值，識別得到的剛度參數最大誤差為0.06%.說明通過廣義逆方法由平動響應重構出的角度，角速度和角加速度響應準確度不高，基于最小二乘遞推算法進一步進行識別的剛度參數結果也不夠理想.從識別的物理量來看，阻尼的識別效果整體要差于剛度參數，考慮噪聲后誤差更大，阻尼真值很容易被測試噪聲所湮沒.

考慮5%的噪聲存在時，對轉角進行重構的工況1的剛度參數識別最大誤差達到21.13%，分析其原因，主要是因為加速度積分成速度和位移產生的誤差和廣義逆方法本身的誤差累積，使得誤差進一步放大.考慮5%噪聲時，采用角度、角速度真實值的工況2剛度參數識別的最大誤差為2.94%，說明了最小二乘遞推算法具有一定的抗噪能力.整體來說，采用重構轉角值的工況1所識別的參數誤差較大，因此可以考慮通過傳感器直接測量轉動響應.

5? ?試驗研究

5.1? ?MEMS陀螺儀傳感器的角度測量精度驗證

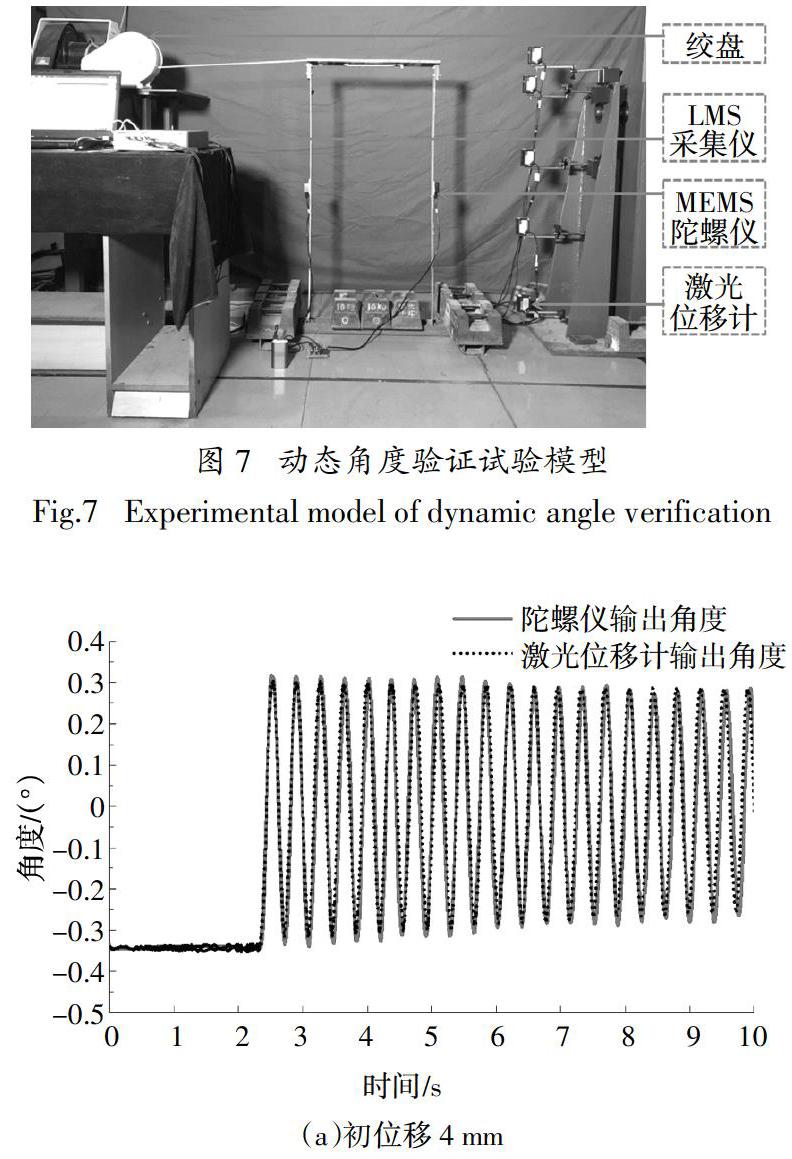
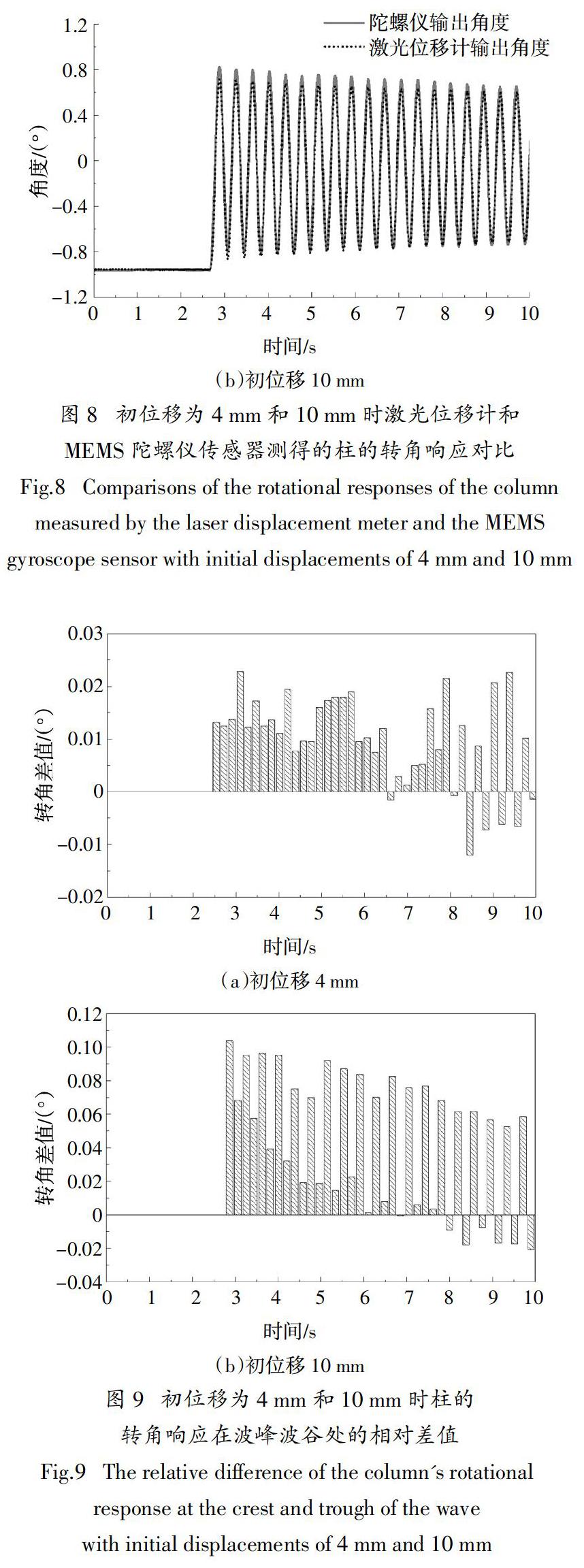
有效識別物理參數的前提是保證測量的響應信息準確，因此需對動力試驗條件下MEMS陀螺儀傳感器的角度測量精度進行驗證. 試驗結構模型為如圖7所示的門式鋼框架結構，選取其右側柱構件為試驗對象. 柱尺寸為B × W × L = 5 0 mm × 3 mm ×1 060 mm，角度信號由維特智能HWT901B陀螺儀傳感器采集，共布置2個MEMS陀螺儀傳感器，位于門式框架右側柱構件中間位置的傳感器用來采集柱的轉動響應，左側柱構件上對稱布置的傳感器用來保持框架結構質量對稱.位移信號由基恩士IL300+IL1000激光位移計采集，其量程為280 mm，精度為0.7 mm. 試驗共布置5個激光位移計，頂端布置1個用于控制初位移，后4個以23 cm為間距等距離布置，用于測量柱的平動響應.試驗時，通過左側絞盤牽引施加2 ～ 10 mm不等的初位移.然后剪斷繩子瞬時釋放，結構恢復自由振動狀態. 每隔2 mm設置一次工況，共5組試驗. 由第2節所述的轉動響應曲線擬合方法可以得到激光位移計測得的轉動時程響應，與MEMS陀螺儀傳感器測得的轉動時程響應結果對比如圖8和圖9所示. （篇幅所限，僅展示初位移分別為4 mm和10 mm時的測量結果.）

通過上述圖片中MEMS陀螺儀傳感器與激光位移計輸出的角度的對比，可以明顯觀察出：隨著初位移的增大，MEMS陀螺儀傳感器與激光位移計輸出的角度差值也隨之增大.分析誤差產生的原因主要為以下兩點：1）根據動轉角擬合原理，應保證激光位移計發射的激光，門式框架受激勵后振動的二維平面，絞盤上繩子施加力的方向均在同一個平面內.由于現場試驗條件限制，很容易產生誤差. 2）激光位移計所測量構件平面的表面不夠平整. 綜合來看，在結構初位移為10 mm以內，可以基本保證MEMS陀螺儀傳感器進行動態角度測量的精度在0.1°.

5.2? ?MEMS陀螺儀傳感器的時域識別

5.2.1? ?試驗模型

試驗結構模型為如圖10所示的一個3層2跨的鋼框架結構，框架模型整體尺寸為1 m × 1.6 m，首層層高為0.6 m，二、三層層高為0.5 m，框架柱的間距0.5 m，梁、柱均采用50 mm × 3 mm的截面尺寸的鋼薄板. 梁柱節點處采用尺寸為∟18 mm × 18 mm × 3 mm的角鋼加M6（螺紋直徑6 mm）×16（螺紋長度16 mm）的螺栓連接，如圖11所示. 框架模型構件采用Q235鋼，取0.5 m長的鋼梁構件做測試，實測質量密度為7 832.60 kg/m3，用脈沖錘擊法識別梁的固有頻率，然后利用固有頻率識別梁的彈性模量，經過10次測試平均得到鋼梁的彈性模量為2.072 × 1011 N/m2，基于彎剪型結構計算模型，可得鋼框架結構的層間抗彎剛度參數EI的計算值為22.622 1 N/m.

5.2.2? ?測試方法及結果

用脈沖錘擊法對框架結構進行動力測試，由于結構完全對稱，可將框架左側與右側梁柱連接節點的轉動響應視為相等，僅在一側布置MEMS陀螺儀傳感器.沖擊激勵使用美國PCB力錘，加速度信號由PCB系列壓電式加速度傳感器333B40采集，角度及角速度信號由維特智能HWT901B陀螺儀傳感器采集，使用LMS Cadax-8動態信號分析儀進行試驗數據結果的采集. 為保證框架結構質量對稱，在每根梁上未布置MEMS陀螺儀傳感器的一側，均放置了100 g的配重磁鐵用于模擬MEMS陀螺儀傳感器的質量.

試驗中采用力錘在鋼框架的3#節點位置水平從左至右激勵一次，力錘的錘擊力測量結果經放大后如圖12（a）所示，采樣頻率為100 Hz，采樣點數為12 000個.

傳感器測點布置如圖11所示，加速度傳感器布置于7#、8#、9#測點，采集得到的加速度響應信號如圖12（b）所示. MEMS陀螺儀傳感器布置在4#至9#測點，采集的框架中間4#、5#、6#測點的角度和角速度響應信號分別如圖12（c）和圖12（d）所示. （篇幅所限，未展示框架右邊7#、8#、9#測點的角度和角速度信號）. 對測試得到的各層加速度響應分別進行傅里葉變換，對相應的各階頻率取平均值得到結構的前三階模態頻率，分別為2.073 Hz、6.704 Hz、11.773 Hz.利用采集得到的結構自由振動時的加速度時程曲線的峰值的對數衰減率求得阻尼比，并根據第1和第2階振型的頻率，可以得到剛度阻尼系數b，乘以剛度參數EI可以得到阻尼參數的計算值為0.024 4 N·s/m.

5.2.3? ?結構參數時域識別

框架模型的梁與柱構件等剛度，可視為一般框架結構.模型中所有梁柱構件具有相同的截面尺寸和材料特性，梁的跨度相等，整體結構對稱，基于以下假定對其進行參數識別：1）框架模型的材料為線彈性;2）梁與柱連接節點處采用角鋼加螺栓連接，假設梁與柱的連接有足夠的剛度，如圖13所示，當框架發生彈性變形時，能保持相交的梁柱桿件之間原有的角度不變[26]. 3）框架底層用膨脹螺絲固定于地面，在結構分析中忽略框架的平面外變形.4）梁與柱的軸向變形和剪切變形較之轉動變形可以忽略，因此假設框架同一層內的各梁柱連接節點的水平位移均相等.

試驗結構模型共18個自由度，包含9個平動自由度和9個轉動自由度.基于同一層內節點的水平位移均相等的假設，可將上部結構的平動自由度簡化成3個. 考慮轉角重構和轉角實測兩種工況，由于前者將由平動響應重構轉動響應，所以將9個轉動自由度簡化為3個，后者則考慮所有的轉動自由度.最終兩個工況的計算模型如圖14所示.

已知MEMS陀螺儀傳感器和配重磁鐵的質量均為100 g，根據鋼梁構件的尺寸和質量密度，可求出梁單元的質量，同理可求出柱單元的質量，進而可求得4×4階的單元質量矩陣. 將單元質量矩陣組裝后可獲得框架結構最終協調質量矩陣，轉角重構和轉角實測工況分別采用6×6階和12×12階的協調質量矩陣.根據第3節所述方法，可以構造參數識別的方程式（19），轉角重構工況下直接采用3.2節的公式，轉角實測工況下，當識別第1、2層時，式（19）中：

將響應信息、外激勵、質量矩陣和層高代入上式，由最小二乘遞推算法識別出結構的剛度和阻尼參數如表4所示，剛度參數與阻尼參數的收斂曲線如圖15所示.

從識別結果可看出，轉角實測工況下的剛度參數識別效果明顯優于轉角重構工況，轉角重構工況下的最大和最小誤差分別為20.36%和14.38%，轉角實測工況下的最大和最小誤差分別為13.92%和7.84%.阻尼參數的識別結果受噪聲影響較大，失去參考價值.

分析轉角實測工況下剛度參數識別的誤差產生的原因有以下可能;其一，由加速度響應重構速度、位移響應的過程中，由于存在趨勢項和噪聲，會使得積分結果產生誤差.其二，由于該框架結構的轉動變形較小，而MEMS陀螺儀傳感器的動態測量精度僅為0.1°，因此識別效果不夠理想.其三，受實驗條件限制，由于MEMS陀螺儀傳感器為接觸式傳感器，不能完全測得節點連接處的實際轉動變形，只能以節點附近的轉動變形近似替代.但使用MEMS陀螺儀傳感器測量的轉角精度仍然高于用廣義逆方法重構出的轉角，這為轉動信息的準確測量提供了新的思路.

6? ?結? ?論

基于廣義逆方法重構轉角信息和采用撓曲線擬合的方式重構轉角信息，提出采用商業級的MEMS陀螺儀傳感器測量角度和角速度響應，改變了傳統的僅測試位移類響應的方法，對響應信息進行了直觀補充.然后通過最小二乘遞推算法識別彎剪型結構的剛度和阻尼參數，得出的結論如下：

1）基于撓曲線擬合方法對MEMS陀螺儀傳感器的角度測量精度校驗，主要用來驗證動力試驗條件下測量的角度是否準確.本文采用的陀螺儀傳感器HWT901B在初位移為10 mm內可保證動態角度精度為0.1°，試驗時，測得鋼框架結構的最大位移為4 mm左右，受到力錘激勵后的最大角位移為0.3°左右，其動態角度精度約為0.02°，精度誤差約為6.67%，該傳感器基本可以滿足實驗要求.

2）實際工程中的結構形式更復雜，剛度也更大，相應的轉動響應的振幅更小，因此對使用的傳感器靈敏度要求更高，花費也相對較高.部分位置如節點連接處的轉角如何準確測量、如何采用信號處理算法及誤差補償技術提高MEMS陀螺儀的性能，從而提高其精度仍是值得進一步研究的課題.

3）根據算例分析和試驗研究發現，基于廣義逆理論重構轉動信息的方法需要使用位移、速度、加速度響應分別來重構角位移、角速度、角加速度響應. 試驗時，通常只測量位移類響應中的加速度響應，加速度響應積分成速度、位移響應的過程中會產生誤差. 由位移類響應重構轉角類響應的過程中，會將在位移類響應中累積的誤差帶入轉角類響應. 同時，廣義逆方法本身也存在誤差. 以上原因，導致重構轉角下的剛度參數識別效果不如直接測量轉角理想.

4）采用MEMS陀螺儀傳感器直接測量轉動響應在實測框架中的平均誤差為11.13%.相比于由廣義逆方法重構轉動響應的平均誤差17.07%，誤差減少了5.94%.說明使用最小二乘遞推算法對彎剪型結構進行剛度參數時域識別時，使用轉角響應測量值的方法更好，而且與廣義逆重構轉動響應的方法相比，無需進行復雜計算也不受平動響應的影響.

本文在常規的僅測量平動信息的基礎上補充了轉動信息的實測數據，使時域識別的結構物理參數更為準確，對結構的健康監測具有一定參考價值.

參考文獻

[1]? ? HART G C，YAO J T P. System identification in structural dynamics[J]. Journal of the Engineering Mechanics Division，1977，103（6）：1089—1104.

[2]? ? 李國強，李杰. 工程結構動力檢測理論與應用[M]. 北京：科學出版社，2002：185—191.

LI G Q，LI J. Theory and application of dynamic tests in engineering[M]. Beijing： Science Press，2002：185—191. （In Chinese）

[3]? ? 謝獻忠. 結構動力學系統時域辨識理論與試驗研究[D]. 長沙：湖南大學土木工程學院，2005：1—2.

XIE X Z. Theoretical and experimental researeh ondynamic systemidetification in time domain[D]. Changsha： College of Civil Engineering，Hunan University，2005：1—2. （In Chinese）

[4]? ? 趙昕. 工程結構時域系統識別研究[D]. 上海：同濟大學土木工程學院，2003：7.

ZHAO X. Research on time domain system identification of engineering structures[D]. Shanghai：College of Civil Engineering，Tongji University，2003：7.（In Chinese）

[5]? ? 潘芹，易偉建. 卡爾曼濾波在結構物理參數識別中的應用[J]. 湖南大學學報（自然科學版），2002，29（3）：137—142.

PAN Q，YI W J. Application of extended Kalman filter toidentification of structural parameters[J]. Journal of Hunan University （Natural Sciences），2002，29（3）：137—142. （In Chinese）

[6]? ? LI J，ROBERTS J B. Stochastic structural system identification，Part 1：mean parameter estimation[J]. Computational Mechanics，1999，24（3）：211—215.

[7]? ? 陳雋. 高層建筑損傷檢測中的復合反演理論與試驗研究[D]. 上海：同濟大學建筑工程系，1999：63—66.

CHEN J. Compound inversion theory and experimental study on damage detection of tall buildings[D]. Shanghai：College of Architectural Engineering，Tongji University，1999：63—66. （In Chinese）

[8]? ? 趙昕，李杰. 轉角信息未知條件下的結構參數識別方法研究[J]. 工程力學，2003，20（4）：55—59.

ZHAO X，LI J. Structural parameter estimation with unknown rotational response[J]. Engineering Mechanics，2003，20（4）：55—59.（In Chinese）

[9]? ? DIMSDALE J S. System identification of structures with joint rotation[M]. Berkeley：University of California，1983：34—35.

[10]? EWINS D J，SAINSBURY M G. Mobility measurements for the vibration analysis of connected structures[J]. Shock and Vibration Bulletin，1972，44：105—122.

[11]? MOTTERSHEAD J E，KYPRIANOU A，OUYANG H. Estimation of rotational frequency responses[J]. Key Engineering Materials，2003，245/246：157—166.

[12]? RATCLIFFE M J，LIEVEN N A J. Measuring rotational degreesof freedom using a laser Doppler vibrometer[J]. Journal of Vibration and Acoustics，2000，122：12—20.

[13]? SUN J H，ZHANG J，LIU Z，et al. High-dynamic angle measurement based on laser displacement sensors[J]. Applied Optics，2013，52（23）：5676—5685.

[14]? LEE J J，HO H N，LEE J H. A vision-based dynamic rotational angle measurement system for large civil structures[J]. Sensors，2012，12（12）：7326—7336.

[15]? XIA Y，ZHANG P，NI Y Q，et al. Deformation monitoring of a super-tall structure using real-time strain data[J]. Engineering Structures，2014，67：29—38.

[16]? HOU S，ZENG C S，ZHANG H B，et al.Monitoring interstory drift in buildings under seismic loading using MEMS inclinometers[J]. Construction and Building Materials，2018，185：453—467.

[17]? XU B，CHEN G，WU Z S. Parametric identification for a truss structure using axial strain[J]. Computer-Aided Civil and Infrastructure Engineering，2007，22（3）：210—222.

[18]? SERDAR S，MARIA Q F. Instantaneous damagedetection of bridge structures and experimentalverification[J]. Journal of Structural Control and Health Monitoring，2008，15（7）：958—973.

[19]? 楊業飛，申文濤. 慣性穩定平臺中陀螺技術的發展現狀和應用研究[J]. 飛航導彈，2011（2）：72—79.

YANG Y F，SHENG W T. Development and application of gyroscope technology in inertial stabilization platform[J].Aerodynamic Missile Journal，2011（2）：72—79.（In Chinese）

[20]? VISWANATH A，LI T，GIANCHANDANI Y B. High resolution micro ultrasonic machining （HR-USM） for post-fabrication trimming of fused silica 3-D microstructures[C]// IEEE International Conference on MICRO Electro Mechanical Systems. San Francisco，CA，USA：MEMS 2014，2014：494—497.

[21]? SINGH T P，TSUCHIYA T，TABATA O. Frequency response of in-plane coupled resonators for investigating the acceleration sensitivity of MEMS tuning fork gyroscopes[J]. Microsystem Technologies，2012，18（6）：797—803.

[22]? 陳華，來強濤，郭桂良. 基于正交誤差對準的MEMS陀螺測控電路設計[J]. 湖南大學學報（自然科學版），2017，44（10）：114—121.

CHEN H，LAI Q T，GUO G L. Design of MEMS gyroscope interface circuit based on quadrature error alignment[J]. Journal of Hunan University （Natural Sciences），2017，44（10）：114—121.（In Chinese）

[23]? 趙鶴，王喆垚. 基于UKF的MEMS傳感器姿態測量系統[J]. 傳感技術學報，2011，24（5）：642—646.

ZHAO H，WANG Z Y. MEMS sensors based attitude measurement system using UKF[J]. Chinese Journal of Sensors and Actuators，2011，24（5）：642—646.（In Chinese）

[24]? 朱伯龍，屠成松，許哲明. 工程結構抗震設計原理[M]. 上海：上海科學技術出版社，1982：173—184.

ZHU B L，TU C S，XU Z M. Seismic design principles of engineering structures[M]. Shanghai：Shanghai Science and Technology Press，1982：173—184.（In Chinese）

[25]? AISC-LRFD99 Load and resistance factor designspecification for structural steel buildings[S]. Chicago：American Institute of Steel Construction，1999：1—5.

[26]? 陳為真，汪秉文，胡曉婭. 基于時域積分的加速度信號處理[J].華中科技大學學報（自然科學版），2010，38（1）：1—4.

CHEN W Z，WANG B W，HU X Y. Acceleration signal processing by aumerical integration [J].Journal of Huazhong University of Science and Technology（Natural Sciences），2010，38（1）：1—4.（In Chinese）