機場的士司機的抉擇與管控

摘要 機場是迎接各個地方來客的最前沿、最普遍的陣地，加之機場的服務與管理直接影響著機場的形象與秩序，而這又直接影響到來客對本城市的第一印象，因此關注機場的出租車問題就顯得尤為重要。本文就司機如何抉擇、管理部門為實現高效乘車和司機收益均衡應如何選擇管控措施作了全面分析，并給出了解決方案。

關鍵詞：排隊論;入隊閘;綠色通道

1、問題分析：

問題1

出租車司機的收益是影響其決策的最直接和最根本的因素，而出租車司機的收益又受到排隊的出租車數量、某一時段內的乘客數量、排隊的時間成本、空載費用等各種因素的影響。因此分別表示出了出租車司機選擇A、B方案的收益，最終以等待時間為考量點給出了出租車司機作出A、B選擇時的界定范圍。

問題2

選擇上海浦東國際機場作為樣本，充分考慮到其龐大的吞吐量使其具備的代表性，并找到了上海浦東國際機場2019年9月12日當天內不同時間段的客流量和當地出租車的收費標準，以及出租車司機等待時間所虧損的相應的時間成本，充分考慮到數據本身具有的客觀性和準確性。

問題3

乘車效率是由單位時間內出租車的載客效率和乘客的乘車效率共同決定的，因此，乘車效率問題便可轉化為單位時間內出租車的載客效率和乘客乘車效率的問題。而且只有當出租車的載客效率大于乘客的乘車的效率，才能有效減少乘客“大排長龍”并以“龍的傳人”自稱的客觀現象，最終實現乘車效率的提高。為了更好的保障出租車的進站效率和確保乘客安全安全，我們想到可以通過設立入隊閘來控制出租車進站的時間以及每兩輛車之間的前后間距，有效控制出租車排隊載客的效率。

問題4

要實現司機的收益均衡的要求，主要是給短途載客再次返回“蓄車池”的司機一些優先權，以解決出租車司機選擇乘客和拒載的問題。

2、模型假設：

假設一

出租車的收費標準統一為元/公里.

假設二

忽略出租車載客或空車返回市區某地點時到出租車再次載客返回機場時的時間差和路程.

假設三

每次載客均滿員為4人.

假設四

每列隊伍排隊的乘客數量相等.

假設五

所有數據均為原始數據，來源真實可靠.

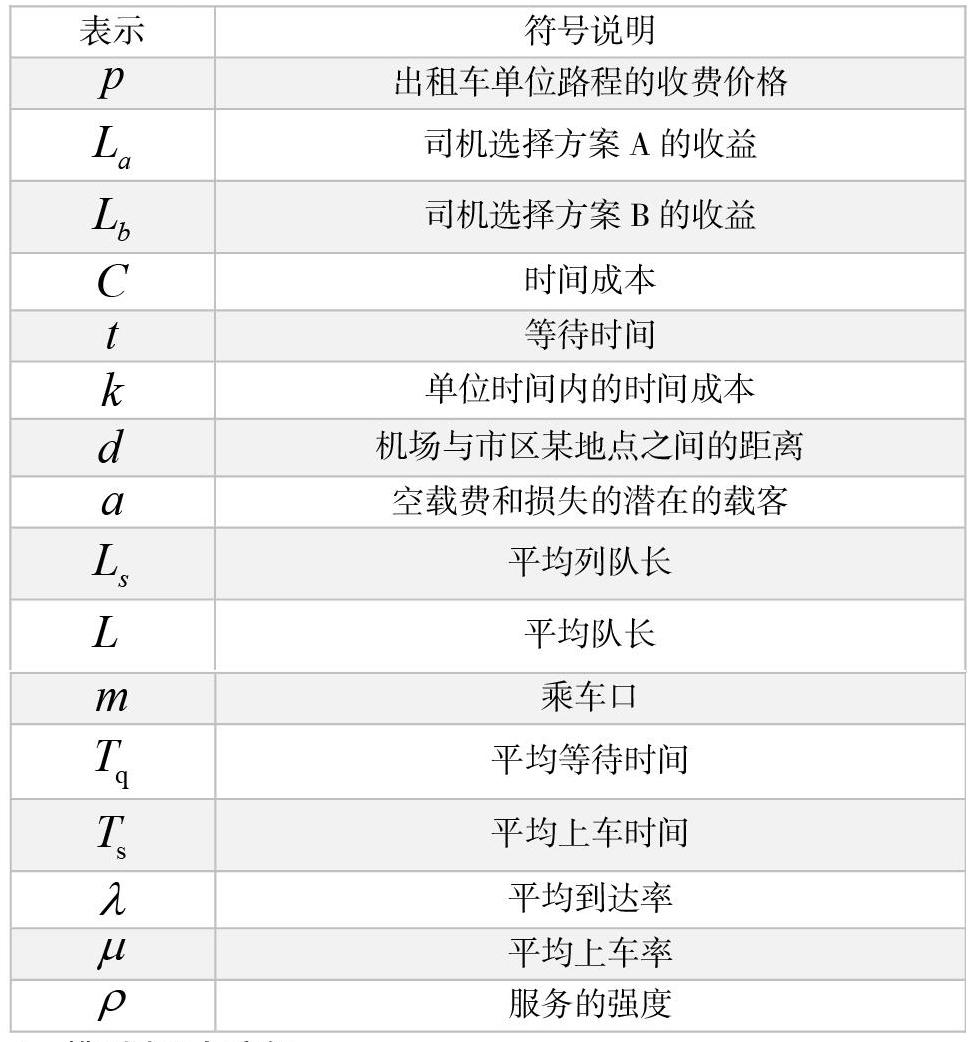
3、符號說明：

4、模型建立與求解：

問題一

設出租車司機的收益為，根據題目對于A、B 兩個選擇的描述易知：

選擇A得考慮時間成本，而時間成本則取決于司機等待時間的長短，故設時間成本為，等待單位時間的時間成本為，等待的時間為，則時間成本為.

設機場到市區某地點的距離為公里，則選A時，出租車司機的總收益為.

選擇B得考慮返回市區的空載費用和可能損失的潛在的載客收益，設空載費用和可

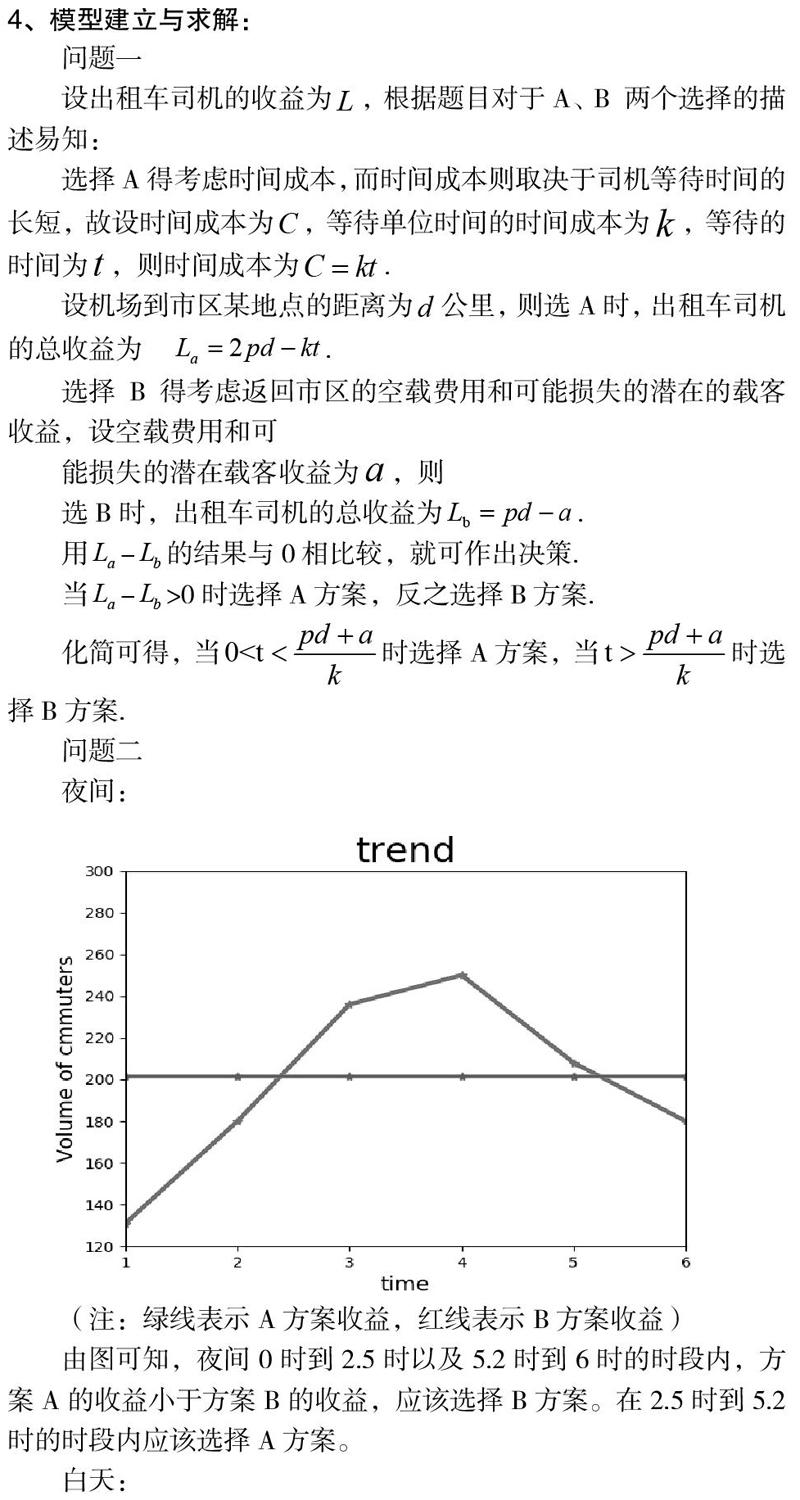
由圖可知，夜間0時到2.5時以及5.2時到6時的時段內，方案A的收益小于方案B的收益，應該選擇B方案。在2.5時到5.2時的時段內應該選擇A方案。

白天：

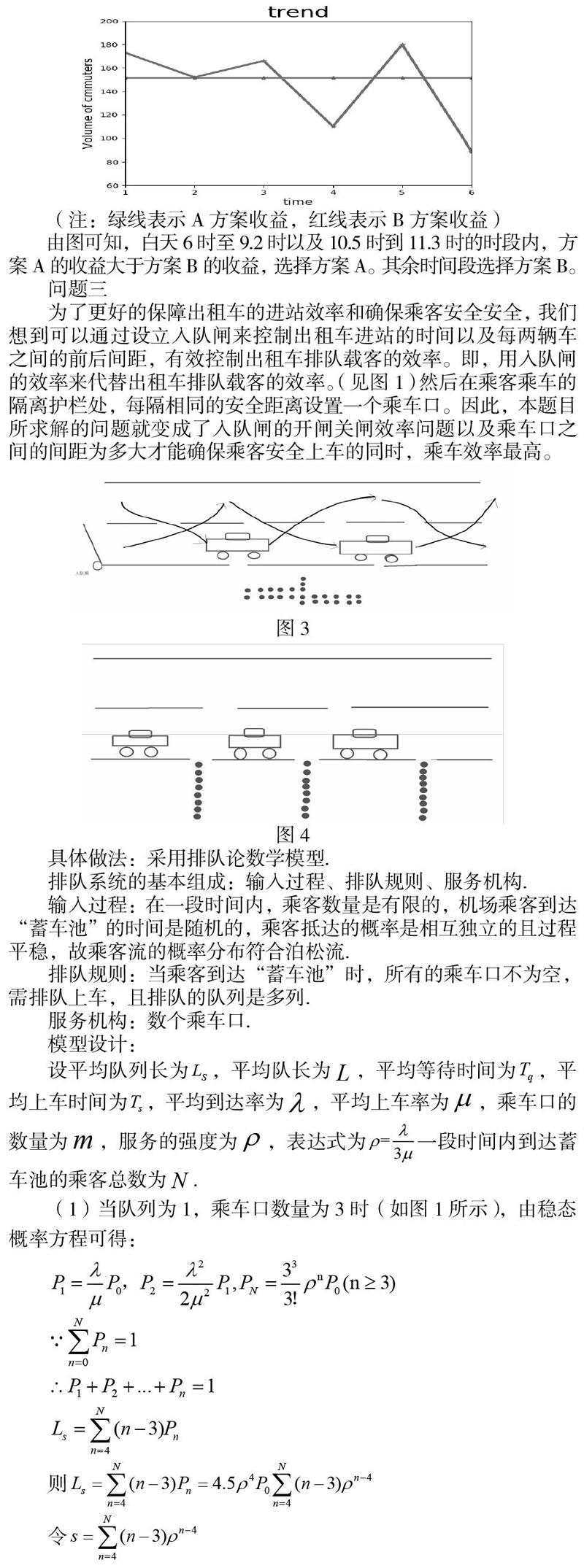
由圖可知，白天6時至9.2時以及10.5時到11.3時的時段內，方案A的收益大于方案B的收益，選擇方案A。其余時間段選擇方案B。

問題三

為了更好的保障出租車的進站效率和確保乘客安全安全，我們想到可以通過設立入隊閘來控制出租車進站的時間以及每兩輛車之間的前后間距，有效控制出租車排隊載客的效率。即，用入隊閘的效率來代替出租車排隊載客的效率。（見圖1）然后在乘客乘車的隔離護欄處，每隔相同的安全距離設置一個乘車口。因此，本題目所求解的問題就變成了入隊閘的開閘關閘效率問題以及乘車口之間的間距為多大才能確保乘客安全上車的同時，乘車效率最高。

具體做法：采用排隊論數學模型.

排隊系統的基本組成：輸入過程、排隊規則、服務機構.

輸入過程：在一段時間內，乘客數量是有限的，機場乘客到達“蓄車池”的時間是隨機的，乘客抵達的概率是相互獨立的且過程平穩，故乘客流的概率分布符合泊松流.

排隊規則：當乘客到達“蓄車池”時，所有的乘車口不為空，需排隊上車，且排隊的隊列是多列.

服務機構：數個乘車口.

模型設計：

設平均隊列長為，平均隊長為，平均等待時間為，平均上車時間為，平均到達率為，平均上車率為，乘車口的數量為，服務的強度為，表達式為一段時間內到達蓄車池的乘客總數為.

（1）當隊列為1，乘車口數量為3時（如圖1所示），由穩態概率方程可得：

相比之下，排三個隊分別從三個乘車口進入，效率最高。

問題四

短途出租車司機由于行駛里程較短，來回的往返機場，與長途載客司機在燃油量、折舊費和載客收益方面會有一定的差距，主要并直接影響載客收益。正是出于這樣的原因，出租車會拒載和選擇乘客，最終造成秩序混亂。為解決這一問題，使得短途載客出租車和長途載客的出租車的載客收益基本達到均衡，理應為短途載客出租車開啟“綠色通道”。

在某一大段時間內，各出租車司機行駛里程相同，折舊費、燃油費大體相同。近似將其平均到某一小段時間內的折舊費、燃油費視為等同。那么只需考慮短途載客司機的時間成本。

設出租車司機在相同路程內所賺的費用為，乘客的人數為，第個乘客的車費為，則 .

設付出的時間成本為K，則司機總的收益為。

只需要盡量的減少短途載客司機不斷往返和在“蓄車池”中排隊所消耗的時間成本K就可以實現收益均衡。

5、誤差分析：

問題一中，我們將出租車司機的經驗值代入決定時間成本的等待單位時間的時間成本，但是，出租車司機的經驗判斷會與實際數據有些許偏差，最終使得決策結果產生偏差。而且問題一中假設所有出租車內均滿員，但實際上，不可能所有車內都滿員，三口之家集體出行游玩的情況還是很普遍的。

由于問題二直接借助問題一所建模型得出結果，所以說最后結果會于實際結果產生偏差。

我們假設不同乘車口的乘客隊列人數相等，但實際生活中，乘客總是會盡可能的選擇人數相對較少的隊列，雖說“眼見為實”，但是每個隊列的排隊乘客數量很難完全相等，這就使得實際結果存在偏差。

將某一大段時間內，各出租車司機行駛里程相同，折舊費、燃油費視為等同，并近似將其平均到某一小段時間內的折舊費、燃油費視為等同，在數據處理方面存在偏差，使得實際結果存在偏差。

6、模型推廣：

本題解決的是由機場出租車引發的系列問題，但是并不局限于機場。像其他的一些旅游大省，諸如西安，每年的省內來客吞吐量也實屬龐大，西安站內也存在著些許由出租車引發的問題，本文的研究分析便可推廣到火車站、高鐵站、地鐵口等來客繁多的領域。

作者簡介：畢笑榮（1998.10），女，山西省文水人，西藏民族大學行政管理專業，本科生。

（作者單位：西藏民族大學）