流體誘發振動研究

黨鵬飛

摘 要：蒸汽發生器是核工業壓水堆中使用非常廣泛，它是一種熱交換設備。正因如此，它能否安全平穩運行對日常生產起著極為關鍵的作用，但是近年來由于振動使得發生器失效的情況越來越多。這方面的原因主要有兩個：一是管束都逐步采用高強度材料，但是材料本身越來越輕薄，剛度越來越小;二是橫掠管束的流速越來越大，造成管束振動的振幅也越來越大。正因如此，這個問題也引起來國內外專家學者的高度重視，越來越多的人也在從事這方面的研究工作。

關鍵詞：漩渦脫落;升力系數;斯特魯哈數;流體彈性不穩定性

0 概述

流體誘發振動指的是與全部浸入流體或輸送流動流體結構的相應有關的各種物理現象。這個術語囊括了流體力與結構中的慣性力、阻尼力以及彈性力之間產生相互作用的各種情況，因此至少涉及到三門學科：①結構力學;②機械振動;③流體動力學。

自古以來，人們早就知道，在流動流體中的圓柱體會產生振動。在古希臘，人們就知道，一根導線會以它自身的固有頻率隨著漩渦脫落而振動。然而直到一個世紀以前，對于一個給定的直徑的圓柱體，才由斯特魯哈建立了漩渦脫落頻率和流動速度之間的關系式。在此之后，各種對于流體誘導振動的研究才真正開始。

目前，在許多領域都存在著流體誘發結構振動的問題，包括航天工業、發電和送變電工程、建筑工程以及海底技術等。這些問題的發生，一般源于不適當的設計。在大多數情況下，用以特定目標所設計的機械部件或結構部件在沒有適當考慮流場的影響時，就會產生振動問題，而對于消除這種有害的振動，工程師們有不同的選擇，然而遺憾的是，通常是代價高昂。

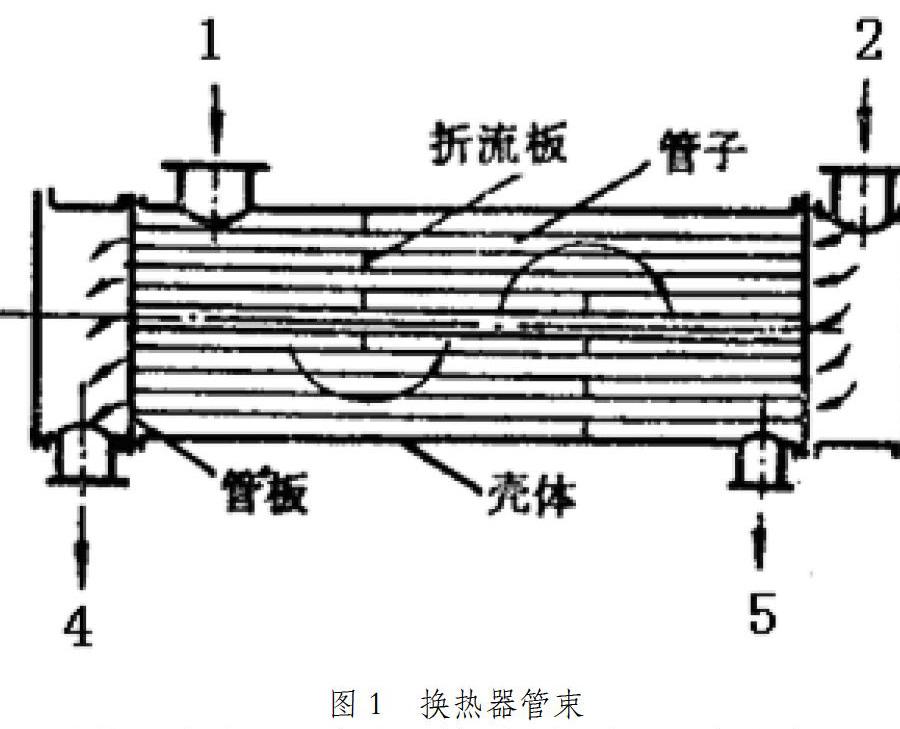
核能反應堆工業存在流體誘發振動的現象由來已久。有些反應堆部件會由于振動導致部件失效，最典型的例子就是蒸汽發生器（如圖1），它可以看做是垂直的單壁管道直通型熱交換器。在1977年的一個原子能發電站中，在試運行過程中，蒸汽發生器有6根管道失效，全部發生在鈉進入口前面。為了研究工作的需要，系統又工作了42天，又發現另外39個管道發生泄漏。原因是由于振動引起的管道之間的相互碰撞和管道與支承碰撞產生的磨損而造成的典型破壞。

流體誘導振動的研究對象是各種振動機理及流體流動中的各種激發力以及構件在這些流體力作用下的運動狀態。通過對運動場中構件上的力及其響應的分折，預測振動模態、振動位置、振幅大小，從而評估構件振動的可能性并辨別其原因，以便采取相應的有效措施，防止因振動而遭受破壞。對縱向流所激發的振動振幅較小，危害性不大，往往可以忽略，只有在流速遠遠高于正常流速的場合，縱向流激振才需考慮。而橫向流在正常流速下就可能引起較大振幅的振動，對傳熱元件危害最大。因此，人們更感興趣的是，橫向流激振的機理以及以這些為基礎的防止振動的方法。很多學者，從不同的側面提出了不同的觀點。到目前為止，學術界比較認同的流體誘導振動機理是“漩渦脫離”、“紊流抖振”、“流體彈性不穩定”、“聲振蕩”等，簡要介紹如下。

1 漩渦脫落（Vortex Shedding）

當流體橫向流過圓柱體時，會在圓柱體的背面兩側交替產生脫離漩渦，即某一刻某一側產生漩渦，而另一側的漩渦恰好與圓柱體脫離;下一時刻則剛好反過來，產生漩渦的一側其漩渦長大、脫離，脫離漩渦的一側則漩渦重新產生、長大，這便是所熟悉的“卡曼渦街”現象。當一側產生漩渦時，相對于另一側來說流體阻力增大，流速減慢，即流體動能小，則其靜壓能增大，相當于產生了一個作用于圓柱體而垂直于流體流向的橫向推力，下一時刻產生漩渦的一側漩渦脫離，脫離漩渦的一側又產生漩渦，則所產生的橫向推力反向。如此循環往復，便產生了一個作用于圓柱體的交變力，即引起圓柱體（換熱管）振動的力。如果漩渦脫離的頻率趨于圓柱體（換熱管）的固有頻率，則可引起共振，形成較大的破壞性。

2 紊流抖振（Turbulence Buffeting）

紊流中脈動變化的壓力和速度場不斷供給管子能量，當紊流脈動的主頻率與管子的固有頻率相近時，管子吸收能量并產生振動。紊流脈動的頻率范圍較寬且具有很強的隨機性。管子僅在其固有頻率附近產生響應。較少導致大范圍的共振響應。由紊流抖振引發的振動不很規律，較少導致大范圍的共振響應。因此認為，紊流抖振不是導致管子破壞的最主要原因，而是產生流體彈性激振的重要原因。

3 流體彈性不穩定（Fluidelatic Instability）

當管束中任何一根管子在其原始位置上發生瞬時位移，都會改變周圍的流場，破壞相鄰管子上力的平衡，使相鄰的管子也產生位移而使其處于振動狀態。這種機械耦聯產生的振動，若能從流體的流動中不斷獲取能量，則振動狀態將延續下去。這就是流體彈性擾動引起的振動。流體彈性激振一般是由其他誘導振動引起管子運動的情況下產生的，流體速度一旦超過某一臨界值并稍有增加時振幅即有大幅度增加，流體彈性力對管束所做功大于管子系統阻尼作用消耗的功，管子的響應振動振幅將迅速增大。

4 聲振蕩（Acoustic Resonance）

聲振蕩一般由漩渦脫離引起。通過漩渦脫離引起管子振動，管子振動則激起周圍媒體（彈性體）的彈性波，彈性波沿換熱器徑向傳播，到換熱器內壁被反射，若換熱器的內徑為該機械波半波長的整數倍，則入射波與反射波疊加后形成聲學駐波。此時，機械波難以向外傳播能量，導致能量不斷積累，產生極大的噪音。聲振蕩只發生在殼程流體為氣體的情況，而對于殼程流體為液體的情況，由于聲波在液體中的傳播速度很大（波長很大），而換熱器的直徑不可能太大，故難于滿足駐波形成的條件。

目前，很多研究者圍繞著四種流體誘導振動機理（漩渦脫離、紊流抖振、流體彈性擾動、聲振蕩）做了大量的工作，無論是理論還是實驗都取得許多進展，提出了不少新的理論解釋與實驗判別式。這些研究在指導換熱器設計方面都起到了積極的作用。但必須指出的是，所有這些預測振動的理論和方法還不足以成功地預測換熱器換熱元件的破壞，能說明的只不過是哪些換熱器容易遭受損壞。缺乏預測精確性的原因是：①通過管束流動的復雜性（有管束上的橫向流、軸向流、旁通流和泄漏流等多股流路。管束兩端的進出口處還存在一定的滯流區。各流路中流體流速的大小和方向在不斷變化，呈不規則的非穩定流動狀態，整個管束處于不均勻力場中，因而管束極易受流體流動的各種激發力而誘發振動）;②流體誘導振動時過多的未知因素;③振動阻尼的不確定性;④換熱元件的磨損和破壞速度難以準確計量等等。

上述的四種激振機理，適用于不同的流體流動狀態。其相對的重要性，可以從表1中看出。

早期的記載換熱器殼程流體誘發振動現象的文獻出現于20世紀30年代至50年代，經歷了半個多世紀的發展，如今這方面的研究成果已經非常豐富，大量文獻都提供了預測和解決這類問題的方法。這其中包括估算分析模型、完全強調結構的模型、與實驗數據相關的半解析模型和完全用于分析和辨識激振機理的單純實驗模型等。Paidoussis，Price，Weaver 等人都對這方面研究的進展作出過總結[1-3]，另外S.S.Chen，Katinas 等人在一些專著中很詳細地分析了這類問題[4-5]。

流體彈性激振機理的第一個研究者是Connors。1970年Connors利用流體剛度控制的機理，提出擬靜態流模型，根據能量平衡分析原理最早提出對比速度環薩/與質量阻尼參數之間的定量關系并用來確定單排管發生流體彈性不穩定臨界流速。這就是最常用的著名Connors公式。1977年Blevins[6]又將此模型推廣應用于多排管。嚴格地講，他們的理論并非真正的解析解，而只是解析解與實驗數據的綜合。

關于換熱器中流體誘發振動的理論研究有很多，Chen[7-8]于1983年提出過用于描述橫流中管束不穩定性產生機理的一般性理論，他指出沒有一個單獨的模型可以解釋所有參數范圍內的不穩定性現象，因此，要解釋不同參數條件下的不穩定性機理需要建立不同的研究模型。

參考文獻：

[1]Paidoussis， M.P.. A Review of Flow-Induced Vibrations in Reactor and ReactorComponents[J]. Nucl. Eng. Des.，1983（74）：31-60.

[2]Price， S.F.. A Review of Theoretical Models for Fluid-Elastic Instability of Cylinder Arrays in Crossflow[J]. J. Fluids Struct.，1995（9）：463-518.

[3]Weaver，D.S.， Ziada， S.， et al. Flow-Induced Vibrations in Power and Process? Plant Components-Progress and Prospects[J]. ASMEJ.PressureVessel Technol.，2000（122）：339-348.

[4]Chen， S.. Flow-Induced Vibrations of Circular Cylindrical Structures[M]. New York， Hemisphere，1987.

[5]Katinas， V.， Zukauskas， et al. Vibrations of Tubes in Heat Exchangers[M]. NY，Begell House，1997.

[6]Blevins R D.Flow induced vibration[M].2nd ed.New York： Van Norstrand Teinhold Company，1977.

[7]Chen S.S.. Instability Mechanisms and Stability Criteria of a Group of Circular Cylinders Subjected to Cross-Flow-Part2： Numerical Results and Discussions[J].ASME J. Vib.， Acoust.， Stress， Reliab. Des.，1983，105（1）：253-260.

[8]Cai Y.， Chen S.S.， Chandra S.. A Theory for Fluidelastic Instability of Tube-Support Plate Inactive Modes[J]. ASME J. PVT.，1992（114）：139-148.