基于集成學習模型的二手房價格影響因素分析
潘楚文 王佩琪 溫嘉琪

摘 要:隨著我國社會經濟不斷發展,房地產行業也逐漸發展擴大。但如今一手房房價過高,而二手房房價適中且地理位置較好,因此人們更傾向購買二手房。本文以廣州市天河區的普通二手房為研究對象,選取了15個變量來建立指標體系以此研究影響二手房的房價因素。本文利用集搜客收集二手房信息資料、R-Studio清洗數據,并使用python編程語言建立評估模型從而研究分析影響二手房價格的因素。
關鍵詞:集成學習模型;統計機器算法;二手房價格;房價影響因素;
如今,我國房地產行業的被越來越多的人關注,迫切需要建立一套科學合理的房地產評估模型,為二手房的購買,銷售、和其他行為提供有價值的參考。從“中國房價行情”官網中發現二手房平均價格基本呈上升趨勢;從2019年3月到2019年6月價格上升趨勢穩定在約5萬元/平米。隨著科學技術的不斷創新發展,研究人員已將機器學習算法應用于房地產評估模型,并在實踐中不斷優化算法。如王勇勝[1]首先構建線性回歸模型、時間序列等五種單一評估模型,田一梅[2]首先采用灰色系統對某市生活用水量進行預測,其次將預測結果作為輸入,代入偏最小二乘法回歸(PLS)模型,結果表明預測誤差更低。因此,本文將基于集成學習模型來研究分析二手房影響因素。
1.數據收集與預處理
首先分析歸納二手房交易網站,主要有房屋基本信息、社區配套設施和社區概況等信息,本文提取部分數據信息[3]。為了收集本文所需更為詳細的天河區二手房數據,運用集搜客GooSeeKer的層級采集獲取天河區二手房房源詳細資料。依據內在規則在第一層數據采集下,挖掘第二層詳細數據,通過MS謀數臺與DS打數機運行工作,搜集天河區的第二層數據資料,此次收集共有1100個數據。
同時,為了提高數據挖掘的質量,使用R語言對數據進行清理。這些數據處理技術在數據挖掘之前使用,大大提高了數據挖掘模式的質量并減少實際挖掘所需的時間。
2.理論基礎
2.1隨機森林算法
隨機森林被稱為當前最好的算法之一,2001年Breiman Leo[4]等人提出了隨機森林算法,不僅減少預測誤差,還可以衡量特征變量的重要性。近年來,它以被廣泛應用于經濟、管理等領域。
隨機森林算法的基本步驟如下[5;6]:
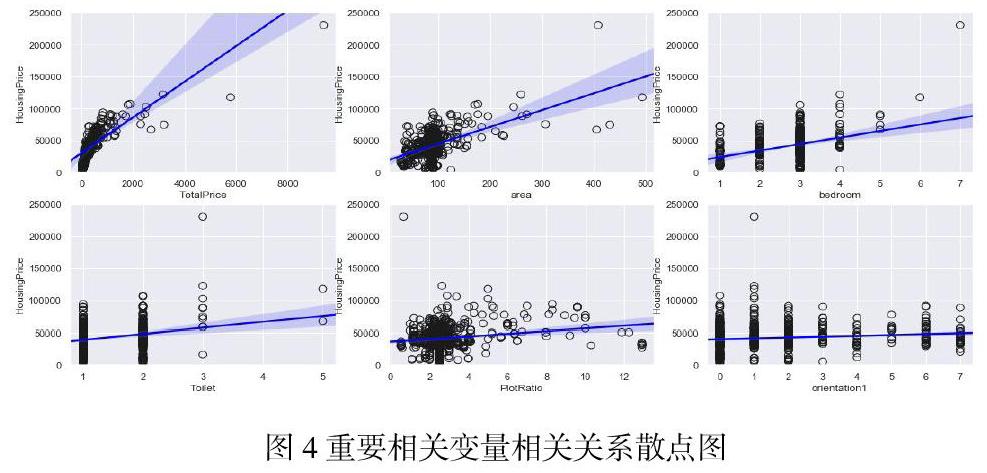
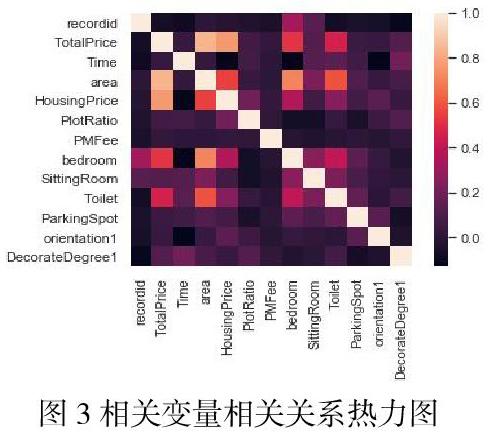
2)采用Bootstrap方法,從訓練集中隨機抽取n個樣本作為新的數據集;
3)基于新數據集構建決策樹,并對決策樹的每個節點,重復一下步驟,直到節點的樣本數達到設定的最小值nmin: 從P個特征值中隨機取m(m 4)根據基尼系數或信息增益率準則,從m個隨機特征變量中選擇最終要的特征變量,分為兩個部分; 輸出B棵樹,針對分類和回歸不同問題的預測,對新樣本X*在每棵樹進行預測,記第b棵樹的新樣本點X*預測為: 分類對新樣本點X*的預測結果為: 2.2梯度提升算法 1)初始化: 2)for m=1 to M 計算負數梯度: 2.3極限樹算法 Extra-Trees(Extremely randomized trees,極端隨機樹)算法與隨機森林算法非常相似,并且由許多決策樹組成。極限樹與隨機森林的主要區別: 1)Random Forest應用的是Bagging模型,Extra Tree使用的所有的樣本,只是特征是隨機選取的,因為分裂是隨機的,所以結果在某種程度上要比隨機森林好。 2)隨機森林在隨機子集中獲得最好的分支屬性,而Extra Tree完全隨機地獲得分支值,從而實現決策樹的分支。 當特征屬性為類別的形式時,隨機選擇具有某些類別的樣本為左分支,將具有其他類別的樣本作為右分支;當特征屬性是數值的形式時,隨機選擇一個處于該特征屬性的最大值和最小值之間的任意數,當樣本的該特征屬性值大于該值時,作為左分支,當小于該值時,作為右分支。這樣就實現了在該特征屬性下把樣本隨機分配到兩個分支上的目的。然后計算此時的分叉值(如果特征屬性為類別的形式,可以應用基尼指數;如果特征屬性是數值的形式,可以應用均方誤差)。遍歷節點內的所有特征屬性,按上述方法得到所有特征屬性的分叉值,我們選擇分叉值最大的那種形式實現對該節點的分叉。從上面的介紹可以看出,該方法比隨機森林更具隨機性。 2.4極端梯度提升 XGBoost(eXtreme Gradient Boosting)全名叫極端梯度提升,xgboost歸根到底屬于boost集成學習方法最終的學習器表示如下: 2.5模型組合Stacking 1992年Wolpert提出集成學習Stacking算法,主要組合多個不同學習器提高預測效果。Stacking算法分為初級學習器和次級學習器。集成學習Stacking算法首先數據集分為訓練集(Training Data)和測試集(Test Data)。 第一層初級學習器:訓練集采用5折交叉驗證,其中訓練模型數據集(Learn)占4/5,驗證模型數據集(Predict)占1/5,首先選擇第一個評估模型Model 1 ,用數據集(Learn)訓練模型,將訓練好的模型對數據集(Predict)進行預測,在第一次交叉驗證后,預測結果記為a1,同理訓練集對測試集(Test Data)進行預測結果為b1,這樣經過五次交叉驗證,訓練集得到的預測結果為(a1、a2、a3、a4、a5),將其合并為一列多行的矩陣A;測試集的預測結果為(b1、b2、b3、b4、b5),對各部分預測值對應相加求平均值,結果記為矩陣B,以上步驟為Stacking中第一個基本學習器為Model 1的完整算法流程。 第二層次級學習器:矩陣A為訓練集,矩陣B為測試集,構建簡單的多元線性回歸模型,其中第j個單一評估模型Model j對第i個訓練樣本點的預測值,作為新的訓練集中第i個樣本的第j個特征值,即解釋變量為不同模型的預測值,被解釋變量是實際因變量值。 3.各階段二手房重要影響變量 本文參照安居客等二手房網站,將房地產評估的相關文獻與天河區的內涵和特征相結合,選擇總價格、房齡、面積、朝向、樓層與層數、裝修程度、房子單價、容積率、物業費用、臥室、客廳、衛生間、參考首付、參考月供、綠化率共15個指標,進而將特征指標分為定性變量與定量變量細分。 采用箱線圖方法研究房齡對房價的影響程度,如圖1所示: 從圖1可知,不同房齡階段的房價變化趨勢比較明顯。1900年到1993年的房齡對房價的影響尚未穩定,而1995-1997年、19998-2000年房價則相對穩,但對比前三年房價有下跌趨勢,隨后2001年到2009年都是逐步回升的狀態,且房價保持穩定,而到了2010年到2019年房價略有下降趨勢。由此可知,購房者可能偏向于01-09年的二手房。 采用直方圖方法研究二手房房價,如圖2所示: 為了研究在不同階段影響二手房價格的因素。本文首先將房價離散化。其中通過圖2可以看出,說明天河區房價主要集中在50K/平方-70k/平方。 同時,由于隨機森林具有更好的準確性和穩健性,為了研究所選特征變量是否很好解釋并將房價劃分,因此本文使用隨機森林,對變量重要性度量,利用R語言“RandomForest”包構建模型,進行相關因素的離散化。 3.1影響二手房房價重要因素 顏色越深代表重要性以及影響程度越大,顏色越淺代表重要性以及影響程度越小。特征變量的重要程度主要分為3種,如圖3所示: 3.2影響二手房房價相關因素 從圖可以看出特征變量的相關程度主要分為6種,如圖4所示: 3.3影響二手房變量重要性 采用隨機森林對變量重要性的度量,測量的特征變量重要性程度不同,其十分重要特征和一般程度的特征如圖5所示: 4.總結 本文得出的結論為天河區的二手房房價主要集中在50k/平方-70k/平方。通過15個變量來建立指標體系以此研究影響二手房的房價因素。房齡、樓層與房價為負相關,地段的繁華程度則與房價呈正比。通過相關關系散點圖得出總價、地段與參照首付是消費者首要考慮最重要的因素。其次,房型與綠化率也和房價有相關關系,房型的面積的大小與房價呈正比關系。隨著生活質量的提高,人們也越來越注重有氧生活,因此,綠化率也會成為參考首選之一。除了以上的因素外,房子的朝向、物業費用、容積率等因素也對房價有重要的影響。 本文以廣州市天河區二手房價格為例,基于天河區的特征變量建立評估模型,進而得出每一種因素的相關影響程度。由于采用單一評估模型可能不具有一致性,而采用模型stacking算法則有效解決這一問題。但是,本文也存在不足,由于本文搜集的數據是二手房網站的掛牌數據,無法獲取最終交易價格,因此收集到的數據受到限制,構建的評估模型可能會受到一些影響。 統計機器學習作為統計學領域的新生事物,它的強操作性預示了它不是一個循規蹈矩、墨守成規的形式與手段,更是為統計學的長遠發展帶來了新的曙光與希望。 參考文獻: [1]王勇勝,薛繼亮.基于多種模型組合的我國2015年人口總數預測[J].西北農林科技大學學報(社會科學版),2009,9(1):75-79 [2]田一梅,汪泳,遲海燕.偏最小二乘與灰色模型組合預測城市生活需水量[J].天津大學學報.2004,37(4):322-325. [3]張漢中,張倩,董起航等,大數據下基于房屋交易網站的數據獲取的二手房價格走勢分析——以上海為例[J].黑龍江科技信息.2017(21):142-143. [4]Breiman L.Radom forests[J].Machine Learning.2001,45(1):5-32 [5:6]呂曉玲,宋捷.大數據挖掘與統計機器學習[M].北京:中國人民大學出版社.2016. 作者簡介: 潘楚文(1999-), 女,廣東省廣州人,廣東培正學院2017級經濟學統計學專業在讀學生。 王佩琪(1998-), 女,廣東省廣州人,廣東培正學院2017級經濟學統計學專業在讀學生。 溫嘉琪(1998-), 女,廣東省江門人,廣東培正學院2017級經濟學統計學專業在讀學生。

