解析法時域分離入、反射合成波方法研究
楊 明
(中交第一航務工程勘察設計院有限公司,天津 300222)
引 言
波浪反射導致近岸結構物靜水面的波浪荷載、樁柱的剪切力荷載增大,威脅建筑物穩定性。將波浪視為一種信號的話,從信號分離域角度可將目前波浪反射分離的研究成果歸為頻域和時域兩類。自由波指擾動力消失后僅在重力作用下繼續傳播的波浪[1],自由波分離方法的研究成果眾多。
早期的分離方法基于波能守恒觀點,利用快速傅里葉算法,計算波浪平均的整體反射系數,并分離出組成合成波的許多個(理論上應是無限個)初相位、頻率不等的簡諧波的入射波振幅。受制于線性波理論的假設條件,該類方法對波浪平穩性要求很高,且集中于頻域分離[2],若要分離局部合成波信號傳播過程中時間域的波浪特征參數信息,必須借助時域分離。
1995年Frigaard等[3]采用數字濾波原理建立的時域分離方法。將波浪幅值時間序列作為數字濾波器的輸入信號,利用波浪反射后的特征值變量,即振幅響應算子及理論相位變化值構建傳遞函數;同年 Zhu[4]基于線性系統觀點建立了不需計算相位差和波幅值的傳遞函數法,但僅局限于規則波的分離;2002年Sun等[5]提出了希爾伯特變換解析法分離不規則波。前述方法基于線性波理論,2010年Ma[6]采用 Morlet小波構建波面信號時間序列的解析形式,提出適用于非線性作用明顯的入反射波的分離方法。
1 傳遞函數法

圖1 傳遞函數法反射模型
1.1 分離原理

由式(3)易知,kΔx=nπ條件下存在奇異解,應用時兩處浪高儀間距應避開半波長整數倍[7]。
1.2 數字濾波器設計
1.2.1 傳遞函數
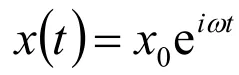

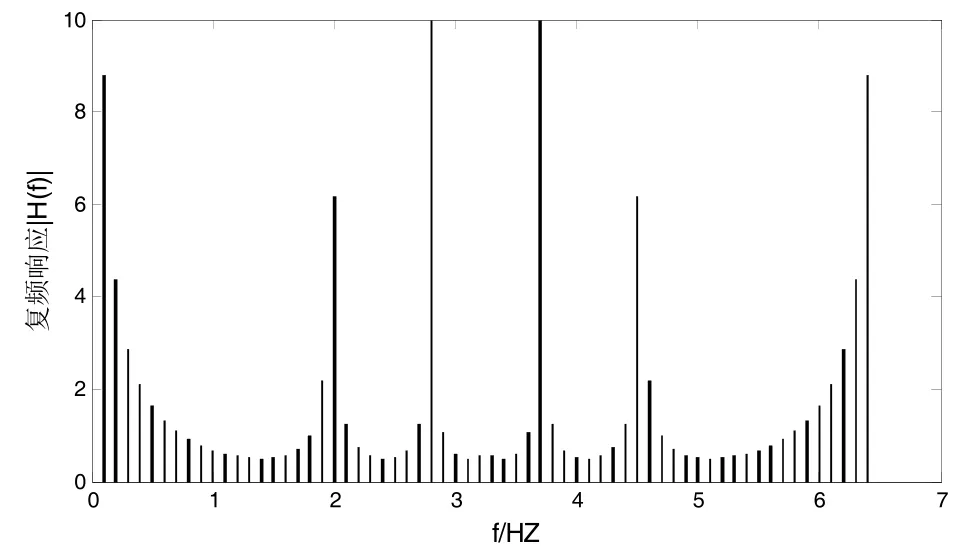
圖2 濾波器的復頻響應
復頻響應函數是關于中心對稱的。圖2對應N=64,Δf=0.1Hz條件下濾波器的復頻響應示例。
1.2.2 濾波器系數
復頻響應函數進行逆離散傅里葉變換,得到的脈沖響應函數即為有限時序的濾波器系數:

ηp-j和hj分別指代t=j?Δtfilter時刻波面高度和濾波器系數,圖3為N=64,Δf=0.1Hz時濾波器系數示例。
1.3 傳遞函數法的計算步驟
1)遵循Goda[7]兩點法的奇異解條件合理布置測點,采集波面數據;
2)明確長度N,迭代逐個計算采樣頻率的波數;
3)由式(4)確定傳遞函數H1(f)、H2(f)表達式,計算所有采樣頻率的振幅值系數C;

圖3 濾波器系數
2 希爾伯特變換解析法
2.1 解析信號的性質
采集波浪數據通過希爾伯特變換給出解析表達,得此波浪序列的瞬時相位和瞬時模[5]。

2.2 分離原理


希爾伯特變換法分離時,采集波列信號表示為:

2.3 希爾伯特解析法的計算步驟
1)遵循Goda[7]兩點法的奇異解條件合理布置測點,采集波面數據;
2)卷積計算,對采集信號作希爾伯特變換得到η(t)解析表達式的虛部g(t);也可對采集信號作快速傅里葉變換得到F(ω),由式(12)得解析信號的傅里葉變換表達式Z(ω),而后再作逆傅里葉變換得g(t);
3)確定采集信號的解析形式后由式(15)可得入反射波的解析表達,該復數域函數的實部即為入反射波浪的時域波面信號。
3 Morlet小波變換解析法
小波變換(wavelet transform,WT)是基于短時傅里葉變換拓展出的一種時頻分析方法,其時頻窗口函數具備可調性,可同時實現信號頻域和時域信息的局部化分析。
Morlet小波在海浪譜分析中應用廣泛,利用Morlet小波變換構造信號的解析形式可表示信號的頻譜包絡以及瞬時相位。
時間序列信號xn(t)的連續小波變換可表示為:
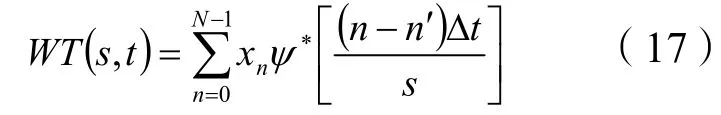
式中:WT(s,t)是小波變換系數;s是尺度因子,表示與頻率有關的伸縮;n′是時間平移因子;ψ*的星標代表共軛,ψ是基本小波ψ0的無量綱化:

小波變換的窗口函數是在“n′-s”域的二維尺度平面,其尺度和平移參數可自適應性調節,在高頻部分具有較好的時間分辨率特性,在低頻部分具有較好的頻率分辨率特性。
連續小波變換式(17)直觀便于理解,但實際計算時為簡化計算根據卷積定理參照下式進行:

Morlet小波的傅里葉變換表示為:


這里s0=2Δt表示最小尺度;J表示最大尺度,尺度參數δj與分辨率成反比,Morlet基本小波中取0.5。
小波變換的逆變換:
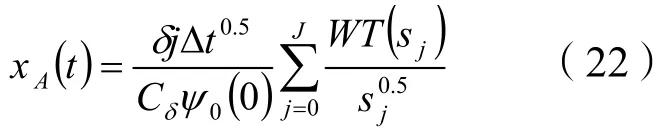
解析信號xA(t)的實部為時間序列x(t),重構因子Cδ:

Ma[6]利用Morlet小波變換分離頻率成分復雜的不規則波:借助其局部分析特性,逐個獲取波浪中各尺度組成波的解析信號,給出各個頻率(尺度)下組成波的入反射波時間序列其解析表達,再進行Morlet小波逆變換,即得入反射波的時域波面信號。
4 結 語
本文結合Frigaad[2]傳遞函數法以及Sun[5]和Ma[6]兩種解析法進行對比研究。二維自由波的時域分離流程示意參見圖4。
1)Frigaad傳遞函數法基于線性系統理論,考慮數字濾波前后僅僅相位和幅值改變,頻率不變。波浪反射過程與之類似,增加計算頻率范圍,其與輸入信號頻率存在重疊的部分就越多,有助于提高精度。
2)希爾伯特解析法不需計算相位差和波高,應用于不規則波時,首先作傅里葉變換需借助Fourier變換給出各分頻波的初相位和波高,逐個就分頻波分離計算,再將結果線性疊加即得不規則波反射系數。
3)Morlet小波變換解析法的貢獻在于解決了非平穩波浪入反射波的分離。
4)借鑒頻域分離方法[2],基于波浪淺水變形理論以及多普勒色散關系,所有時域方法也可相應拓展到斜坡地形以及水流存在條件時二維自由波的入反射波分離。
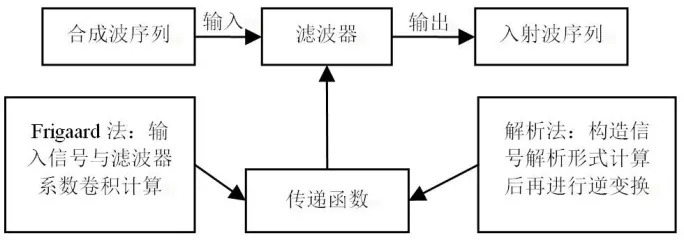
圖4 自由波時域分離流程

