樁靴貫入結構性粘土時鄰近樁水平響應數值分析

孫 凱，王建華，范怡飛

（1.天津大學 水利工程仿真與安全國家重點實驗室，天津 300072；2.天津大學 巖土工程研究所，天津 300072）

引 言

導管架平臺是海洋能源開發工程中常用的固定式平臺，其基礎常為多腿單樁或群樁基礎。自升式鉆井船常被用來為沒有自備鉆機的導管架平臺進行鉆井和修井作業。鉆井船作業時，需要在靠近平臺的位置將大直徑樁靴貫入海床中。受鉆井船作業臂長度限制，隨水深增加，樁靴貫入位置與平臺樁基之間的距離會小于1倍樁靴直徑。美國造船與輪機工程師協會[1]（SNAME）規定：當樁靴與鄰近平臺樁之間的凈間距小于 1倍樁靴直徑時，必須評價樁靴貫入對鄰近樁的影響。

Xie[2]通過離心模型試驗，研究發現樁靴貫入對鄰近樁的影響主要在水平方向上，引起的彎矩和附加應力不可忽略。Siciliano[3]通過離心模型試驗研究了樁靴貫入軟粘土時對鄰近樁的影響以及樁靴貫入后不同凈間距處土剪切強度的變化。研究表明凈間距大于 0.5D時，可不考慮樁靴貫入對鄰近樁的影響。隨著大變形有限元（LDFE）技術的發展，數值仿真分析被大量應用于樁靴貫入過程中對鄰近樁影響等問題的研究中。Tho等[4]、Wu等[5]利用LS-DYNA中的ALE方法對Xie[2]開展的離心模型試驗進行了數值模擬，驗證了大變形數值分析方法模擬樁靴貫入與鄰近樁相互作用過程的可行性。蘭斐等[6]、戴笑如等[7]研究了利用CEL方法（耦合的歐拉與拉格朗日算法）模擬樁靴貫入對鄰近樁影響時，模型歐拉體范圍及網格劃分等對模擬結果的影響。

海積軟土常常具有結構性[8]，當土的結構連結被破壞后，塑性變形就會持續不斷發展。樁靴貫入結構性粘土時對周圍土體的擾動會使土體變得軟弱，導致結構性土中樁靴的擠土作用比非結構性土中弱，土體向插樁坑內回淤比非結構性土中劇烈，因此樁靴貫入結構性土時鄰近樁的水平響應與非結構性土中存在差異。Li等[9]通過ABAQUS中ALE算法研究了鉆井船樁靴貫入對鄰近樁基的影響。研究發現當樁靴貫入結構性較強的土時，樁靴對周圍土體的擾動會使結構性土的強度弱化，導致樁靴上部土體回淤加劇且樁靴貫入導致的土體位移減小。本文就樁靴貫入結構性土時鄰近單樁水平響應展開研究。

1 CEL模型中結構性粘土參數設置及檢驗

采用滿足Mises屈服準則的彈塑性本構模型設置結構性粘土參數。Abaqus中可以通過輸入表格自動插值來簡單地設置強化準則。在結構性土應力應變曲線上取點，將所取點的屈服應力及對應的塑性應變輸入到plastic中來描述結構性粘土的應力應變關系。

1.1 無側限抗壓強度試驗應力應變曲線

通過向含水量為 90 %的飽和高嶺土（液限45 %）泥漿中加入3 %標號Q42.5的普通硅酸鹽水泥并攪拌均勻，在 16 kPa的上覆壓力下雙面排水固結養護7天的方法制備結構性粘土[10]，待固結完成后利用所制備的結構性粘土進行無側限抗壓強度試驗，得到的應力應變曲線如圖1所示。

從圖1試驗結果可得人工制備結構性粘土強度存在峰值。在達到峰值強度之前，其應力應變曲線近乎是一條直線。在達到峰值強度之后，強度隨著應變的增加而降低。為簡化參數設置，我們假設結構性土在達到其峰值強度su之前是完全彈性的，應力應變曲線為過原點的直線；在達到峰值強度后，假設結構性土的強度會隨著應變的增加而線性降低，當應變為 15 %時達到其殘余強度sur。人工制備的結構性粘土假設的應力應變曲線如圖2所示。

圖1 無側限抗壓強度試驗應力應變曲線

圖2 人工制備結構性土假設應力應變曲線

1.2 CEL模型中結構性土參數設置檢驗

為檢驗 CEL模型中結構性土參數設置能否準確地定義結構性土強度的軟化特性，在 Abaqus中使用 CEL方法模擬土的無側限抗壓強度試驗，根據人工制備結構性土假設的應力應變曲線定義結構性土參數。

粘土的有效重度取 800 kg/m3，由人工制備結構性土假設應力應變曲線得其彈性模量為810 000 Pa，泊松比取0.49。將表1中數據輸入到plastic中定義結構性土應力應變關系。

表1 結構性粘土參數定義

CEL模型歐拉體直徑9.91 cm，高8 cm。其中心為直徑3.91 cm、高8 cm的圓柱形土體，土體外部為厚度3 cm的空穴。剛性壓頂直徑9.91 cm，厚1 cm。土體與剛性壓頂之間接觸面設為完全粗糙。網格尺寸取0.5 cm。將上述材料賦予土體，使剛性壓頂按照1 cm/s的速度勻速下壓模擬土無側限抗壓強度實驗，模型尺寸如圖3。計算偏應力并進行面積修正，將所得應力應變曲線與人工制備結構性土假設的應力應變曲線對比，結果如圖4所示。

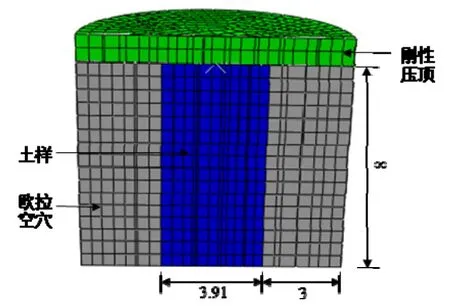
圖3 無側限抗壓強度試驗CEL模型剖面（單位：cm）

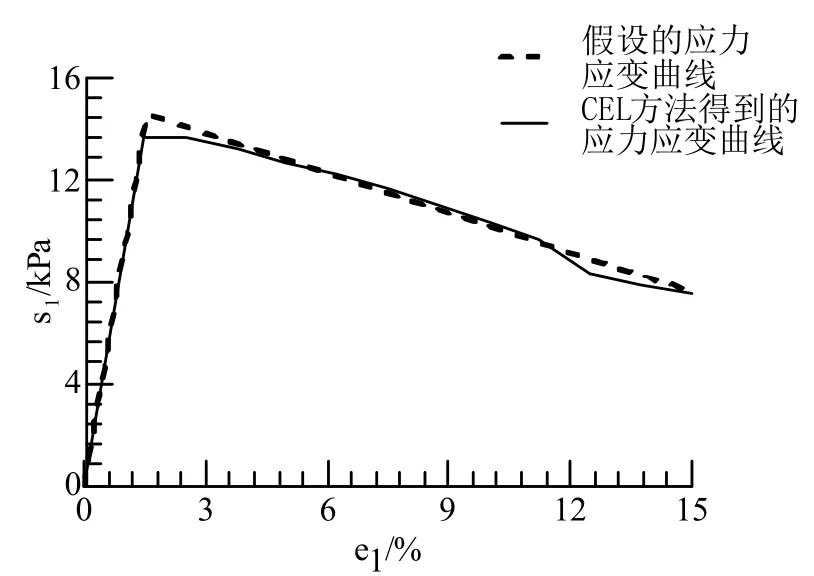
圖4 CEL方法得到的應力應變曲線與假設曲線對比

從圖4可知，由CEL方法模擬無側限抗壓強度試驗得到的結構性土應力應變曲線與人工制備結構性土假設的應力應變曲線基本吻合，說明采用滿足Mises屈服準則的彈塑性本構模型設置結構性粘土參數能夠定義出結構性土強度的軟化特性。

2 CEL模型尺寸及參數設置

模擬樁靴貫入結構性土時鄰近樁水平響應的CEL模型水平方向尺寸為 50 m，豎直方向取55 m。為了容納樁靴貫入土體時樁靴兩側隆起的土體，泥面以上設置深度為5 m的歐拉空穴。泥面以下為50 m深粘土。

樁靴位于泥面處中心位置。樁靴最大直徑D=12 m，樁靴的具體尺寸如圖5。鄰近樁為直徑d=2 m，壁厚0.07 m的鋼管樁，樁長L=40 m。樁靴最大貫入深度為1D。

將土面以下 0～18 m 區域設置為歐拉體，18～50 m區域設置為拉格朗日體[6]。采用六面體單元分別對歐拉體和拉格朗日體進行網格劃分，為保證計算精度并減小模擬結果震蕩，根據戴笑如建議[7]將樁靴中心軸線向外至距鄰近樁外邊緣 2d處的半圓柱形區域劃分為細網格，單元網格尺寸取0.05D。將細網格區域之外的區域劃分為粗網格，單元網格尺寸取 0.1D。豎直方向上，網格尺寸取1 m（0.082D）[11]。有限元模型尺寸如圖6。

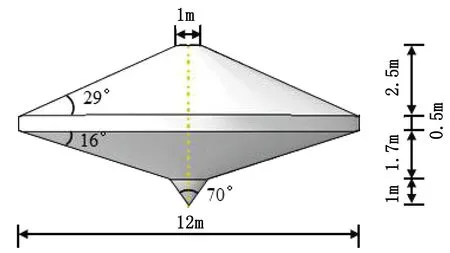
圖5 樁靴尺寸

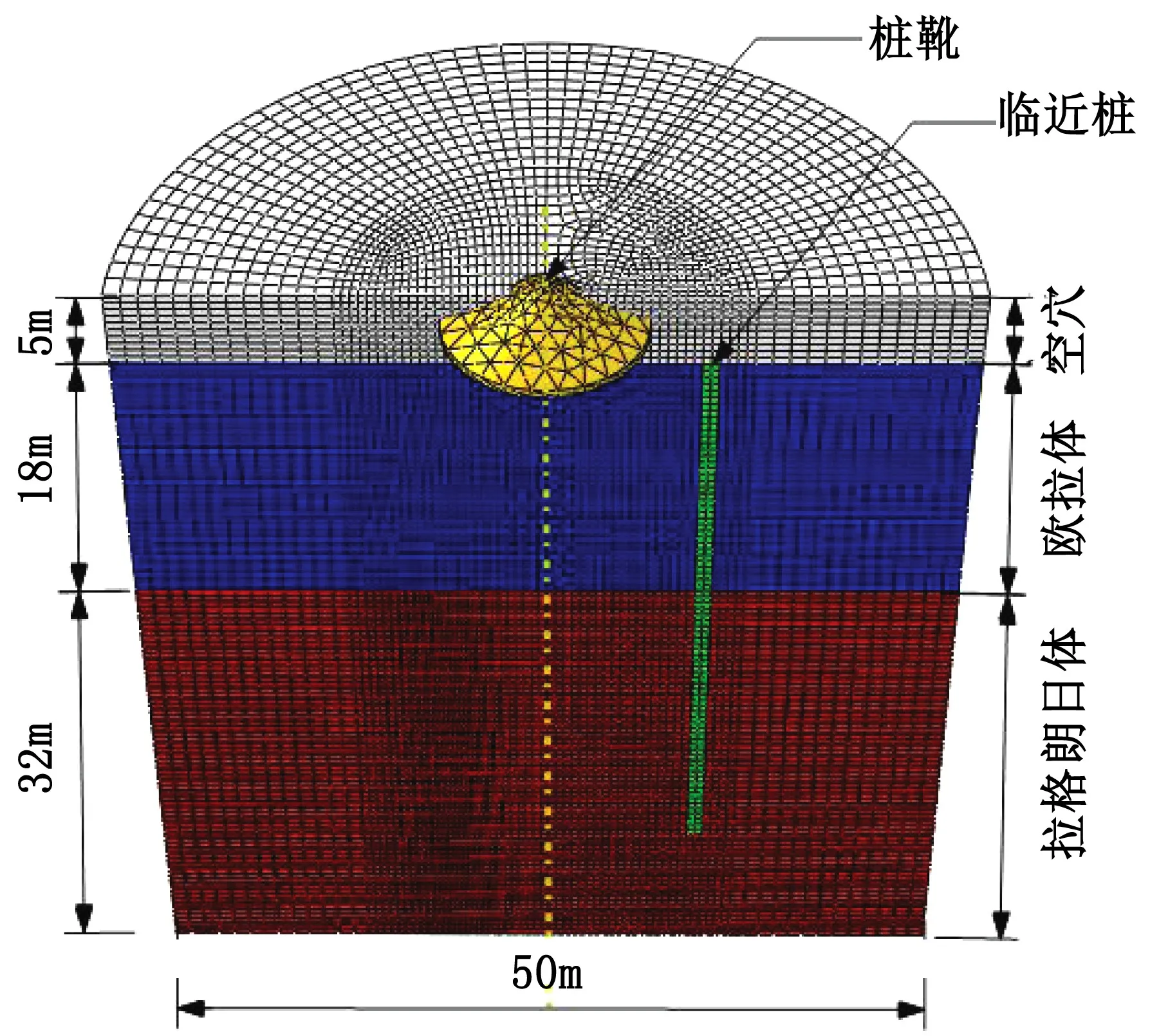
圖6 CEL模型尺寸

為提高計算效率，在 CEL模型中將鋼管樁等效為半徑相同的實體樁，按照抗彎剛度相等原則換算得到實體樁的彈性模量。根據公式（1）算得等效實體樁的彈性模量為52.909 GPa。

式中：E1為鋼管樁彈性模量，取210 GPa；E2為等效實體樁彈性模量；I1、I2分別為鋼管樁和等效實體樁慣性矩。

泥面處粘土的峰值不排水抗剪強度 su為6 kPa。泥面下0～30 m為結構性粘土，su與深度z的關系為su=6+1.5z（kPa）。30～50 m為非結構性粘土，不排水抗剪強度為51 kPa。粘土有效重度取8 kN/m3，彈性模量取150倍su，泊松比取0.49。結構性粘土殘余強度 sur分別取 0.5su及 0.25su。CEL模型中定義的結構性土應力應變曲線為簡化曲線，假設結構性土在達到其峰值強度su之前是完全彈性的，應力應變曲線為過原點的直線，彈性模量E取150su。在達到峰值強度后，結構性土的強度隨著應變的的增加線性降低，當應變為 15 %時達到殘余強度sur。[8,10]

圖7 CEL模型中定義的土的強度曲線

模型接觸設置：忽略歐拉土體與樁靴之間的摩擦；歐拉土體與拉格朗日土體之間切向的極限剪應力設為該處粘土的不排水抗剪強度；土體與樁之間切向接觸為庫倫摩擦接觸，摩擦系數為0.4[4]。

模型邊界條件設置：限制歐拉體及拉格朗日體對稱面及外邊界的水平自由度及底面垂直自由度；海洋平臺樁樁頭與平臺剛性連接，由于平臺的整體剛度較大，平臺樁樁頭可以隨平臺平動，但不可以轉動。樁頭作用有315 kN水平荷載。計算工況如表2所示。

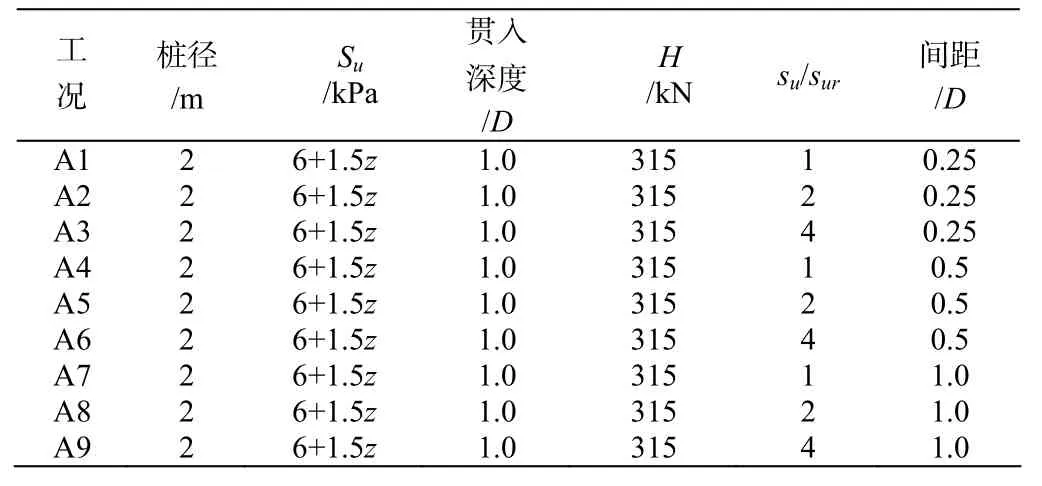
表2 計算工況

3 計算結果分析

3.1 樁身位移及彎矩增量隨樁靴貫入深度變化規律

提取A1、A2、A3工況的樁身位移增量及彎矩增量見圖8。Fan[12]研究了樁靴貫入非結構性粘土時樁靴周圍土體的運動規律。研究發現當樁靴貫入深度為0.25D時，樁靴邊緣土體在水平方向上主要為遠離樁靴的運動。樁靴貫入深度超過 0.5D時，樁靴上方完全被回淤的土體覆蓋，樁靴最大直徑處附近土體發生明顯的繞樁靴流動，樁靴貫入深度以上土體向樁靴位置回淤、貫入深度以下則向外排開。

圖8中正位移增量使樁向背離樁靴方向移動，正彎矩增量使鄰近樁近樁靴面受拉加劇。當樁靴貫入至0.25D時，樁靴向外排開周圍土體使鄰近樁受水平附加荷載的作用。在樁靴擠土作用下，樁頭處彎矩增量及位移增量最大。當樁靴貫入深度超過 0.25D，隨著樁靴的持續貫入，樁靴貫入引起的土體運動逐漸向深處發展，鄰近樁最大正彎矩增量及位移增量的位置由樁頭附近逐漸下移。同時樁靴上部土體向插樁坑內回淤，對樁頭處彎矩增量及位移增量造成影響。在土體回淤影響下，樁頭處彎矩增量及位移增量逐漸減小，并最終發展為負增量。

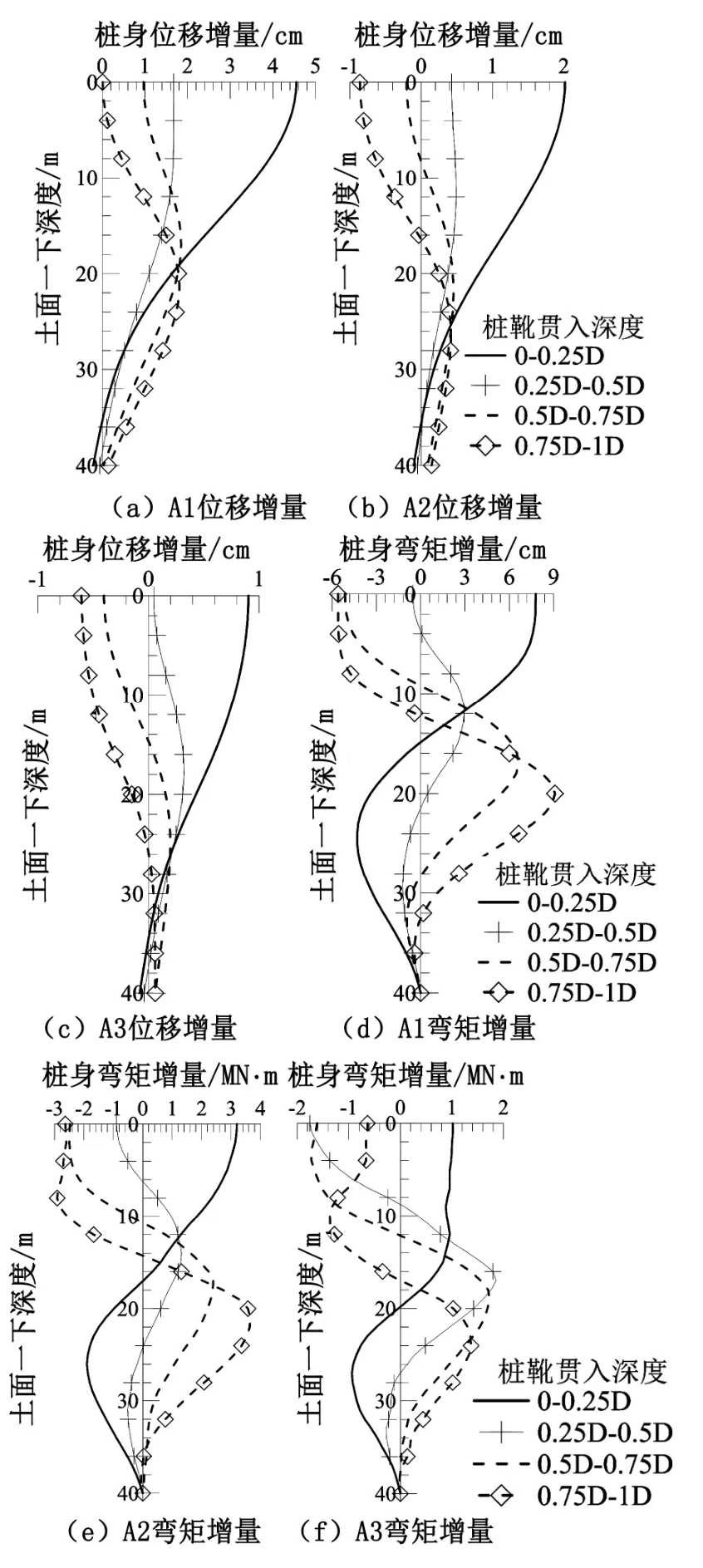
圖8 鄰近樁樁身位移增量及彎矩增量

3.2 殘余強度的影響

相同凈間距下樁靴貫入殘余強度不同的入土深度時0～12 m樁身彎矩增量如圖9所示。結構性土中鄰近樁的最大彎矩增量比非結構性土中小。土的殘余強度越低，鄰近樁中最大彎矩增量越小。

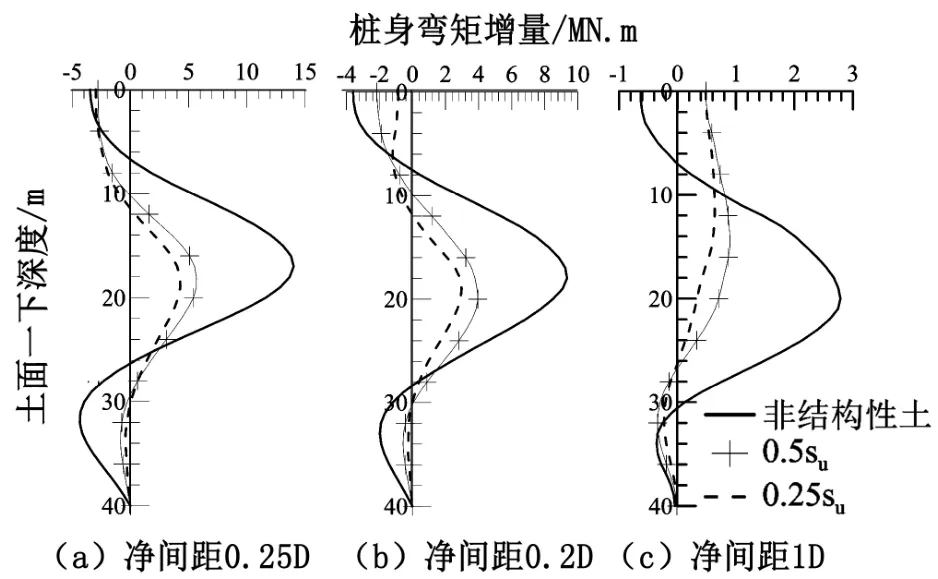
圖9 不同殘余強度的土中鄰近樁樁身彎矩增量

將結構性土中鄰近樁最大彎矩增量相比同凈間距下非結構性土中鄰近樁最大彎矩增量減小的比例定義為 Dm。各工況下鄰近樁最大彎矩增量及Dm值見表3。

表3 鄰近樁最大彎矩增量及Dm值

由表3可知，樁靴貫入結構性土時鄰近樁最大彎矩增量比非結構性土中顯著減小。凈間距 0.25D及 0.5D處，su=2sur的結構性土中鄰近樁最大彎矩增量比非結構性土中降低 58 %左右，su=4sur的結構性土中最大彎矩增量比非結構性土中降低 68 %左右。

3.3 凈間距影響

殘余強度相同的土中不同凈間距下鄰近樁0～12 m彎矩增量如圖10。樁靴貫入擠土作用及土體回淤均隨著凈間距的增大而減弱。鄰近樁中最大彎矩增量及樁頭處彎矩增量絕對值均隨凈間距的增大而減小。當凈間距為1D時，樁靴貫入對鄰近樁周圍土體擾動較小，土體回淤對鄰近樁樁頭處彎矩增量影響小，因此結構性土中凈間距1D處鄰近樁樁頭處彎矩增量仍為正彎增量。

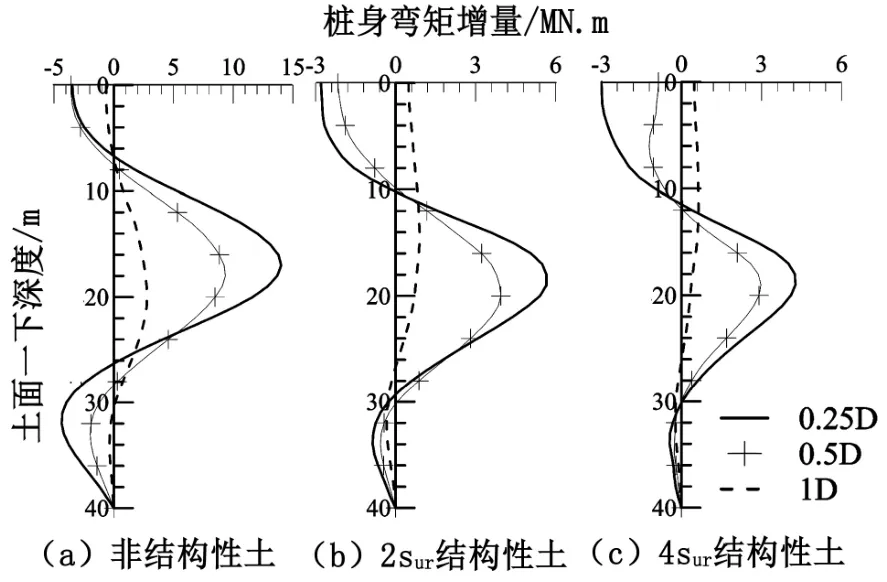
圖10 殘余強度不同的土中鄰近樁樁身彎矩增量

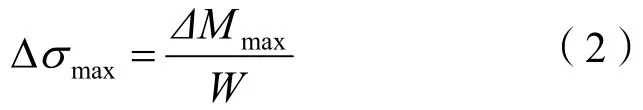
不同凈間距下鄰近樁中最大應力增量占材料屈服應力的比例如圖11所示。

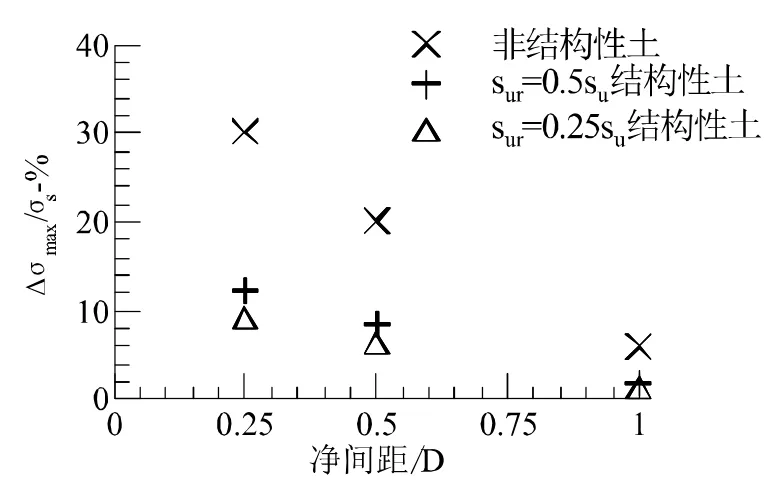
圖11 最大應力增量占屈服應力比例

在非結構性土中凈間距為0.25D、0.5D、1D時鄰近樁中最大應力增量分別占樁屈服應力的30.1 %、21.1 %、6.0 %。凈間距0.25D及0.5D處，su=2sur的結構性土中鄰近樁最大應力增量比su=4sur的結構性土中略大。凈間距 0.25D及 0.5D處，su=2sur的結構性土中鄰近樁的最大應力增量分別占樁屈服應力的12.2 %和8.5 %，su=4sur的結構性土中則為9.2 %和6.4 %。當凈間距為1D時，結構性土中鄰近樁中最大應力增量很小，為樁屈服應力的2 %左右。

3.4 結構性土中樁靴貫入的影響范圍

Xie[2]研究發現樁靴貫入對鄰近單樁的影響主要在水平方向上，引起的彎矩不可忽略。Fan[12]研究發現樁靴貫入土層時鄰近樁中附加應力主要來自樁中附加彎矩。美國造船與輪機工程師協會[1]建議樁靴貫入的影響范圍為 1D。因此以樁靴貫入非結構性土時凈間距1D處鄰近樁最大應力增量占比6.0 %作為樁靴貫入影響范圍的判定標準。用二次正交多項式對結構性土中最大應力增量占比隨凈間距變化曲線進行擬合。結果如圖12。

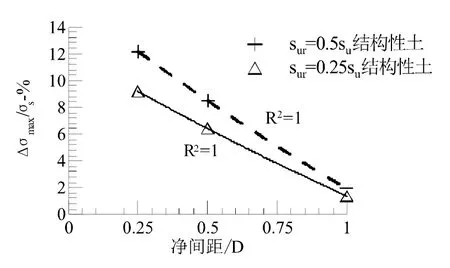
圖12 △σmax/σs隨凈間距變化擬合曲線

sur=0.5su及 sur=0.25su的結構性土中，△σmax/σs隨凈間距變化擬合曲線方程分別為式（3）、（4）。將y=6.0帶入求解，得sur=0.5su的結構性土中樁靴貫入影響范圍為0.68D，sur=0.25su的結構性土中樁靴貫入影響范圍為0.54D。

4 結 語

粘土中當樁靴貫入深度大于0.25D時土體回淤會導致鄰近樁樁頭處位移增量及彎矩增量逐漸減小。樁靴貫入至1D時鄰近樁中最大彎矩增量隨土體殘余強度降低而減小，且隨凈間距的增大而減小；以樁靴貫入非結構性土時凈間距1D處鄰近樁中最大應力增量作為樁靴貫入影響范圍的判定標準，su=4sur的結構性土中，樁靴貫入的影響范圍約為 0.54D；su=2sur的結構性土中，樁靴貫入的影響范圍為0.68D。