某客運專線T型梁受力性能研究

樊少徹 易有淼

(1.西南交通大學土木工程學院 四川成都 610031；2.中鐵第四勘察設計院集團有限公司 湖北武漢 430063)

1 引言

某城際鐵路采用雙線客運專線設計，設計荷載為ZC標準活載，設計車輛行車速度200 km/h，使用壽命100年。本次工程使用的簡支T梁以《通橋(2007)-2201》為藍本設計，該藍本適用于客貨共線活載(ZKH)。為了適應客運專線活載(ZC)的需求，提高設計經濟性、節約造價，對T型梁進行了優化設計。為檢驗設計的合理性，保證工程用梁的安全，抽取兩片梁按《預應力混凝土鐵路橋簡支梁靜載彎曲試驗方法及評定標準》進行靜載彎曲試驗。

2 試驗梁概況

本次試驗梁為某客運專線工程用梁。兩片梁的編號分別為32ZZ0174(直線中梁)和32QZ0483(曲線中梁)。當梁體混凝土抗壓強度達到30 MPa時進行初張拉，達到59.8 MPa時進行終張拉，簡支梁在初張拉和終張拉過程中均未出現滑絲和斷絲現象[1]。兩片簡支T梁長32.6 m，跨度為32 m，端部和跨中截面形式相同，如圖1所示。試驗時兩片梁均未鋪設防水層，梁體預制資料見表1。

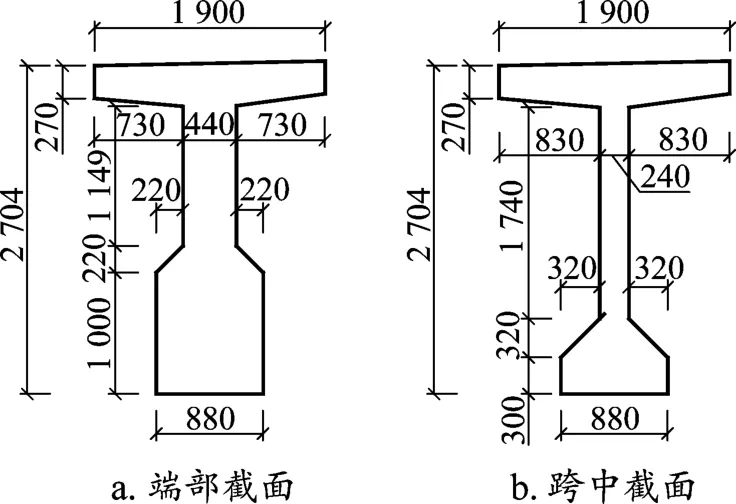
圖1 試驗梁截面形式(單位:mm)

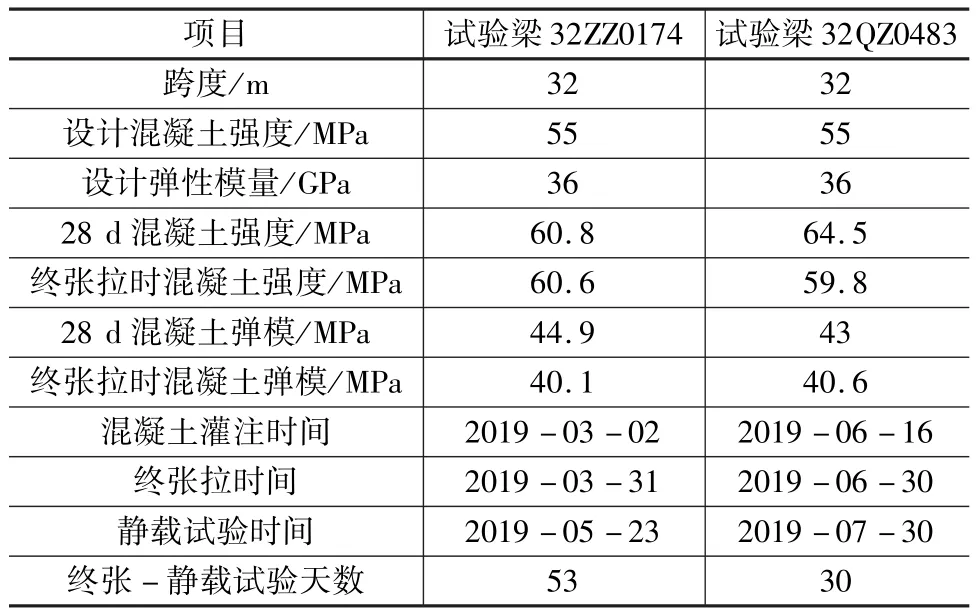
表1 試驗梁基本數據

3 試驗設計

3.1 試驗布置

本次簡支T梁靜載彎曲試驗的設計依據《預應力混凝土鐵路橋簡支梁靜載彎曲試驗方法及評定標準》等效集中荷載采用5點加載[2-3]，各荷載縱向間距為4 m，布置如圖2所示。

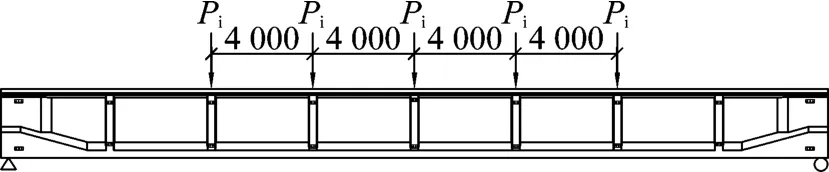
圖2 試驗梁加載布置(單位:mm)

3.2 試驗步驟

(1)試驗梁移入試驗臺座后，在梁頂畫出腹板中心線，從梁體跨中沿內端每隔4 m畫出5個加載點的位置，并在每一加載點下鋪設墊層及墊板。在每一加載點處移入千斤頂，千斤頂底座中心用鋼板墊實，梁跨中中線與中間加力架及千斤頂中心線相重合。

(2)加載前用10倍放大鏡在梁體跨中兩側1/2跨中范圍內的下緣和梁底面進行外觀檢查，對初始裂紋，包括表面收縮裂紋和表面損傷裂紋及局部缺陷用藍色鉛筆描出。

(3)試驗梁的加載分兩個循環進行[4-6]，各級加載時間見表2。

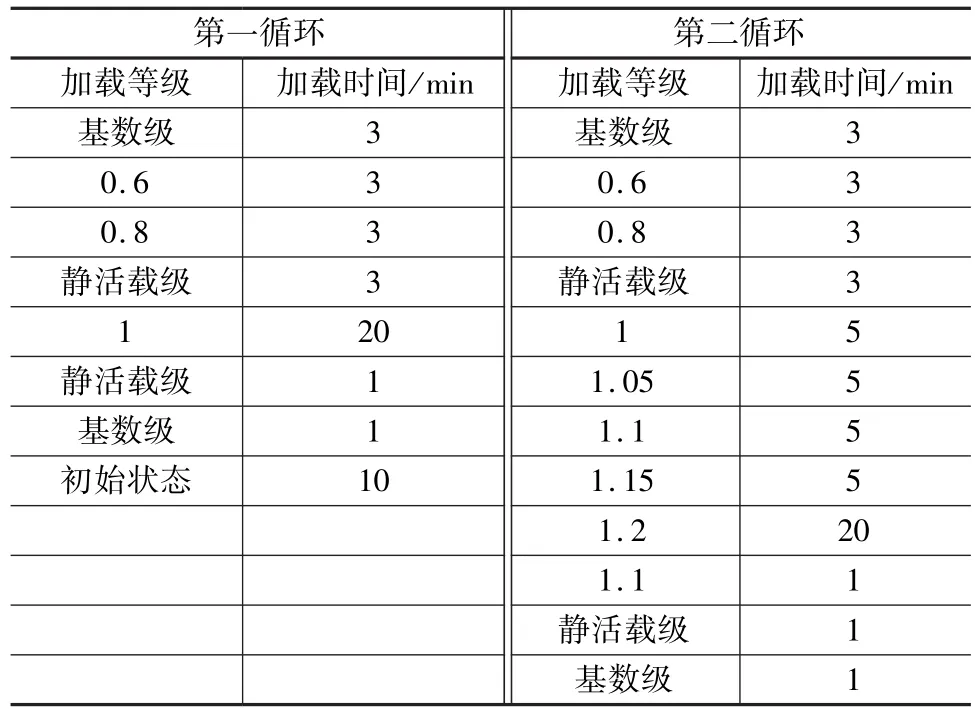
表2 各級加載時間

(4)每級加載后仔細檢查梁體下緣和梁底有無裂縫出現。如出現裂縫或初始裂縫延伸，用紅鉛筆標注，并注明荷載等級，量測裂縫寬度。每級加載后測量梁體跨中和各支座中心截面的兩側豎向位移，以同一截面的兩側平均值作為相應截面的豎向位移量或支點沉降量。跨中截面的豎向位移量減去支點沉降影響量，即為該級荷載下的實測撓度值。

3.3 加載值計算

計算各加載級下的跨中彎矩和荷載值根據《預應力混凝土鐵路橋簡支梁靜載彎曲試驗方法及評定標準》中規定，按公式(1)～(3)計算。

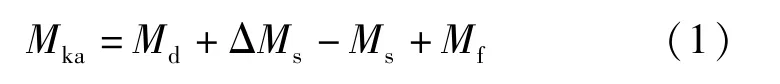
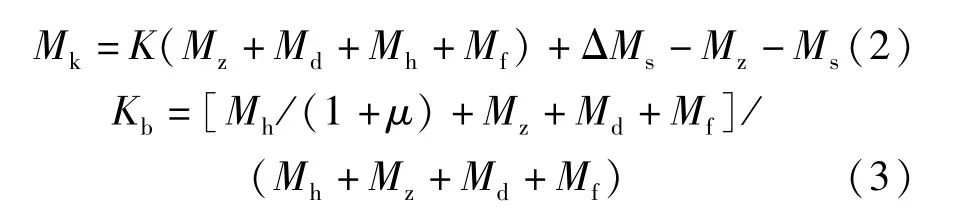
式中，Mka為基數級下的跨中彎矩(kN·m)；Mk為各加載級下的跨中彎矩(kN·m)；Kb為靜活載級下的荷載等級；Md為二期恒載下的跨中彎矩(kN·m)；ΔMs為未完成的預應力損失補償彎矩(kN·m)；Ms為加載設備對跨中的彎矩(kN·m)；Mf為防水層對跨中的彎矩(kN·m)；Mz為梁體質量對跨中的彎矩(kN·m)；Mh為活載對跨中的彎矩(kN·m)；1 ＋μ為動力系數。計算得出各級加載值見表3。

表3 試驗梁各加載級荷載 kN

4 有限元模型構建與分析

4.1 模型建立

采用有限元軟件Midas建立試驗梁空間有限元模型，采用梁單元模擬，支座采用一般支承[7-8]。全橋共117個節點，116個單元，單元劃分見圖3。

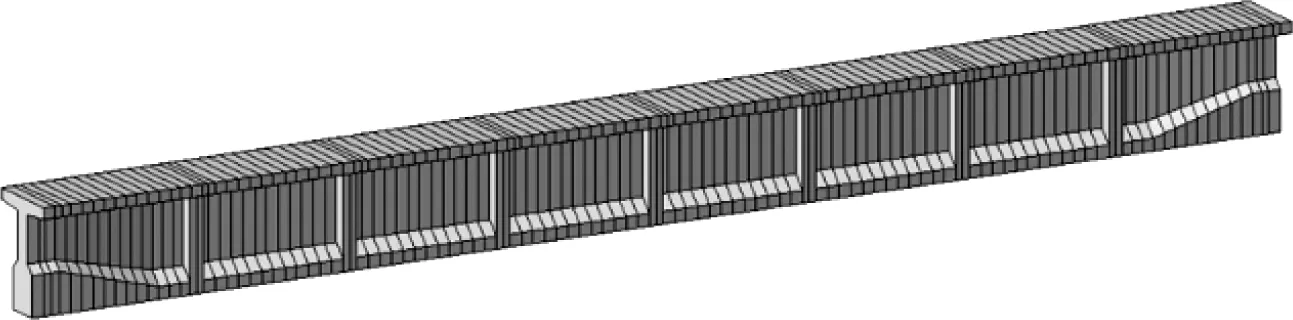
圖3 試驗梁單元劃分

4.2 模型仿真結果

(1)應力分布

在第二循環最大加載等級1.2(626.6 kN)，試驗梁的應力分布如圖4所示。最大應力為17.266 MPa。

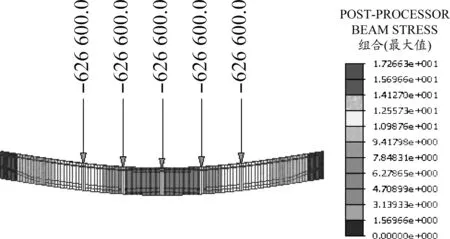
圖4 最大加載情況試驗梁32QZ0483應力分布(單位:MPa)

基數級(Ka)、靜活載級(Kb)和最大加載等級下試驗梁的應力分布如圖5所示。由圖5可以看出，應力在4 m、8 m、12 m、24 m、28 m 處有突然減小的跡象，是由于此處截面突然變大所導致。對圖5中應力分布曲線進行擬合，經試驗，二次函數能取得非常好的擬合效果，擬合優度在97%以上。第二循環所有加載級的應力分布擬合方程見表4。

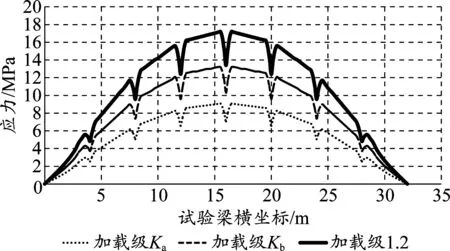
圖5 各加載級試驗梁應力分布(單位:MPa)

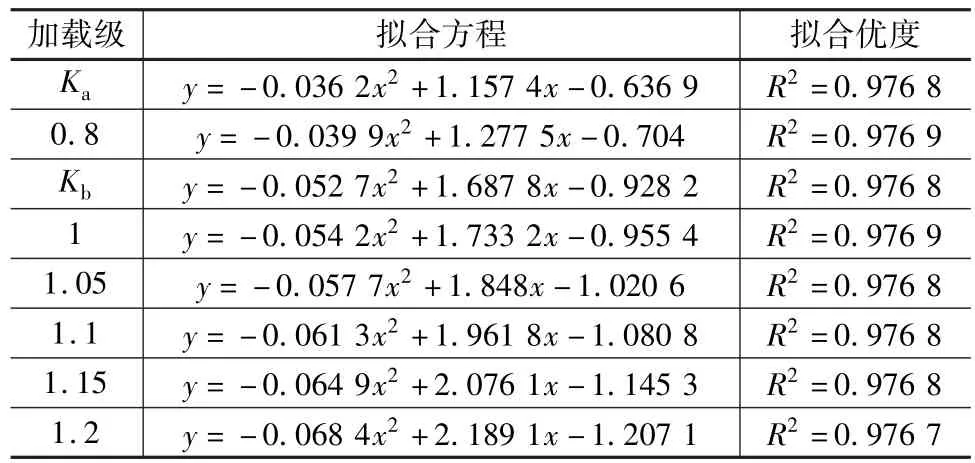
表4 試驗梁各加載級應力分布擬合方程

采用歸納法和因果分析法分析可知，對于截面相同的試驗梁，應力分布主要與梁長度L和加載應力P有關。

在此基礎上歸納總結，基于平截面假定和線彈性理論，提出32 m預應力混凝土簡支T梁應力分布方程，由此可以快速推算出該型梁在任意荷載下，梁體內某一點的應力。

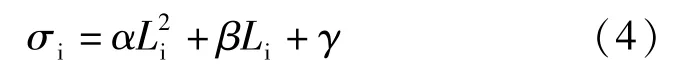
式中，σi為試驗梁i點處應力(MPa)；Li為i點的橫坐標(m)；α、β、γ為系數。

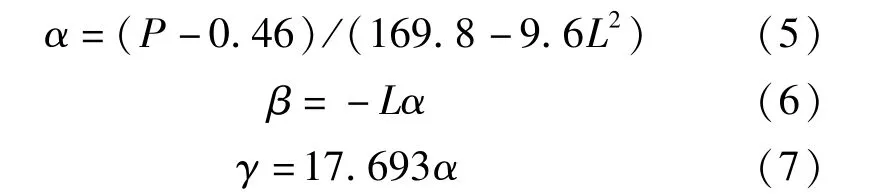
式中，P為加載力(kN)；L為試驗梁長度(m)。

(2)位移分布

在第二循環的基數級(Ka)、靜活載級(Kb)和最大加載級(1.2)下，試驗梁的撓度分布如圖6所示，跨中最大撓度為29.38 mm。

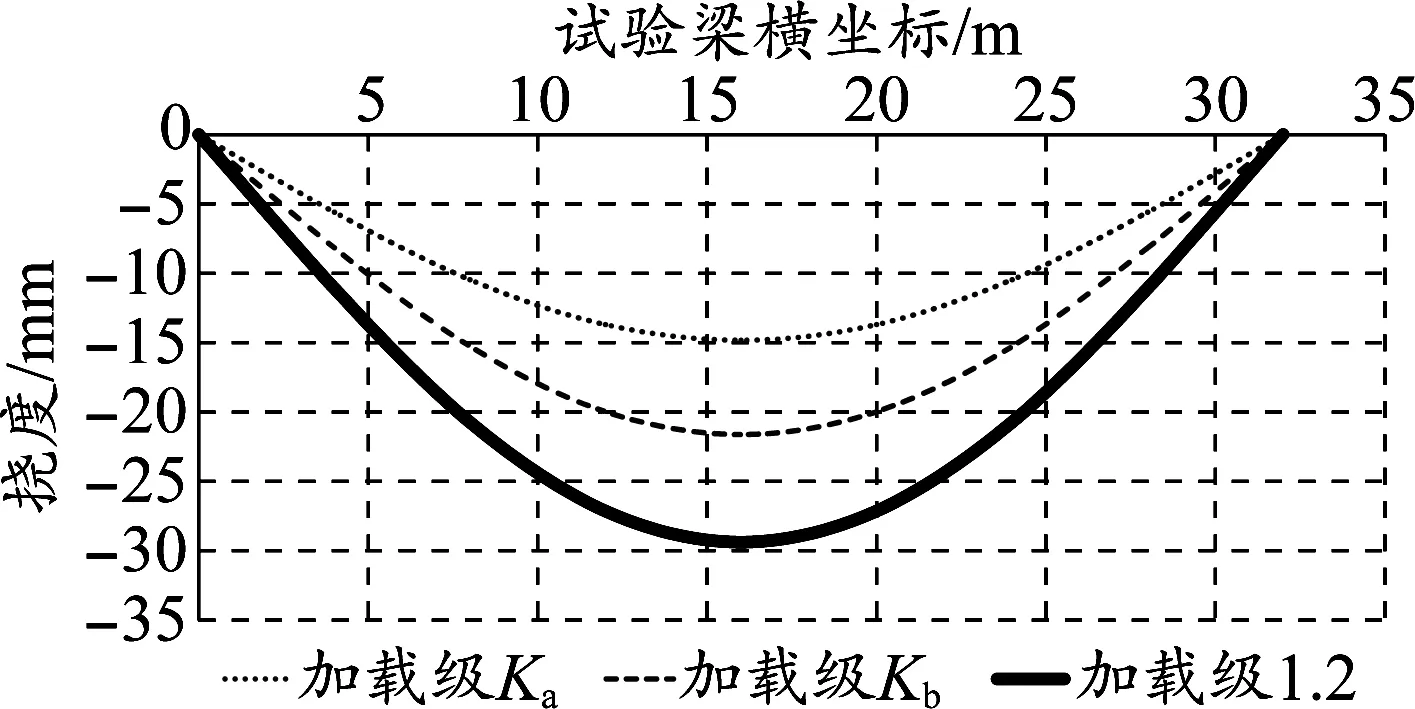
圖6 所有加載級試驗梁撓度分布曲線

采用歸納法和因果分析法可知，對于截面相同的試驗梁，撓度分布主要與梁長度L和加載力P有關。

與公式(4)推導原理相同，在此基礎上歸納總結出32 m預應力混凝土簡支T梁撓度分布方程

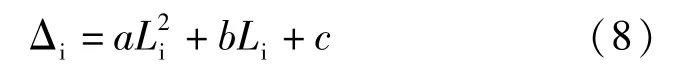
式中，Δi為試驗梁i點處撓度(mm)；Li為i點的橫坐標(m)；a、b、c為系數。

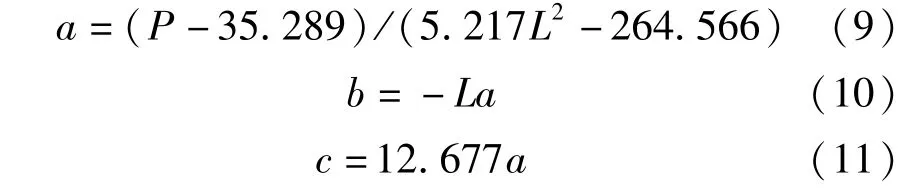
式中，P為加載力(kN)；L為試驗梁長度(m)。

5 試驗結果與評定

5.1 試驗數據分析

兩片試驗梁的靜載撓度試驗數據如圖7所示。

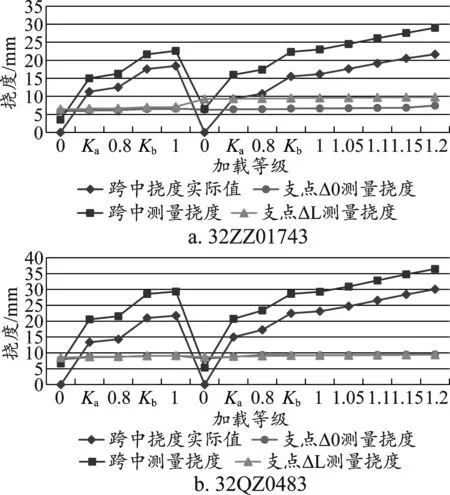
圖7 試驗梁靜載試驗撓度曲線

圖7中跨中實際撓度值是由跨中測量撓度值減去支點沉降影響量計算而得。由圖7可以看出:(1)隨著加載等級提高，跨中撓度逐漸增大；(2)隨著加載等級提高，支座沉降變化減小，并逐漸趨于穩定；(3)在Ka～1.0階段，兩個加載循環撓度值基本一致[9-10]，說明梁體處于彈性工作狀態；(4)試驗梁32ZZ0174扣除支座沉降值，第一加載循環最大撓度為18.43 mm，第二加載循環最大撓度為21.66 mm。試驗梁32QZ0483扣除支座沉降值，第一加載循環最大撓度為21.74 mm，第二加載循環最大撓度為30.06 mm。

試驗梁第二加載循環荷載值與跨中撓度的關系如圖8所示。從圖8可以看出，加載值與撓度基本保持線性關系(擬合優度大于99%)，說明梁體處于彈性工作狀態。但兩條函數的斜率(0.046 2/0.05)有7%左右的差別。由結構力學原理計算出的斜率ρ＝Δ/P＝0.175 13L3/EI，由于兩片梁長度L＝32 m，考慮兩片梁從張拉到試驗間隔時間不同(53 d/30 d)、配筋不同、制作誤差導致梁體彈性模量E有少許不同。

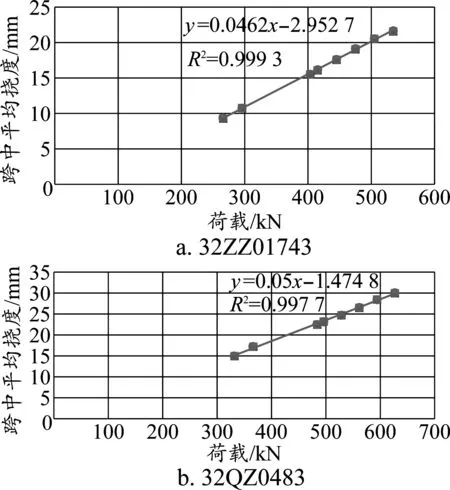
圖8 試驗梁第二加載循環荷載值與跨中撓度關系

試驗梁有限元計算結果與實測結果(第二循環)對比見圖9。可以看出有限元模型與實際擬合得非常好，撓度預測的誤差值在1 mm以內。

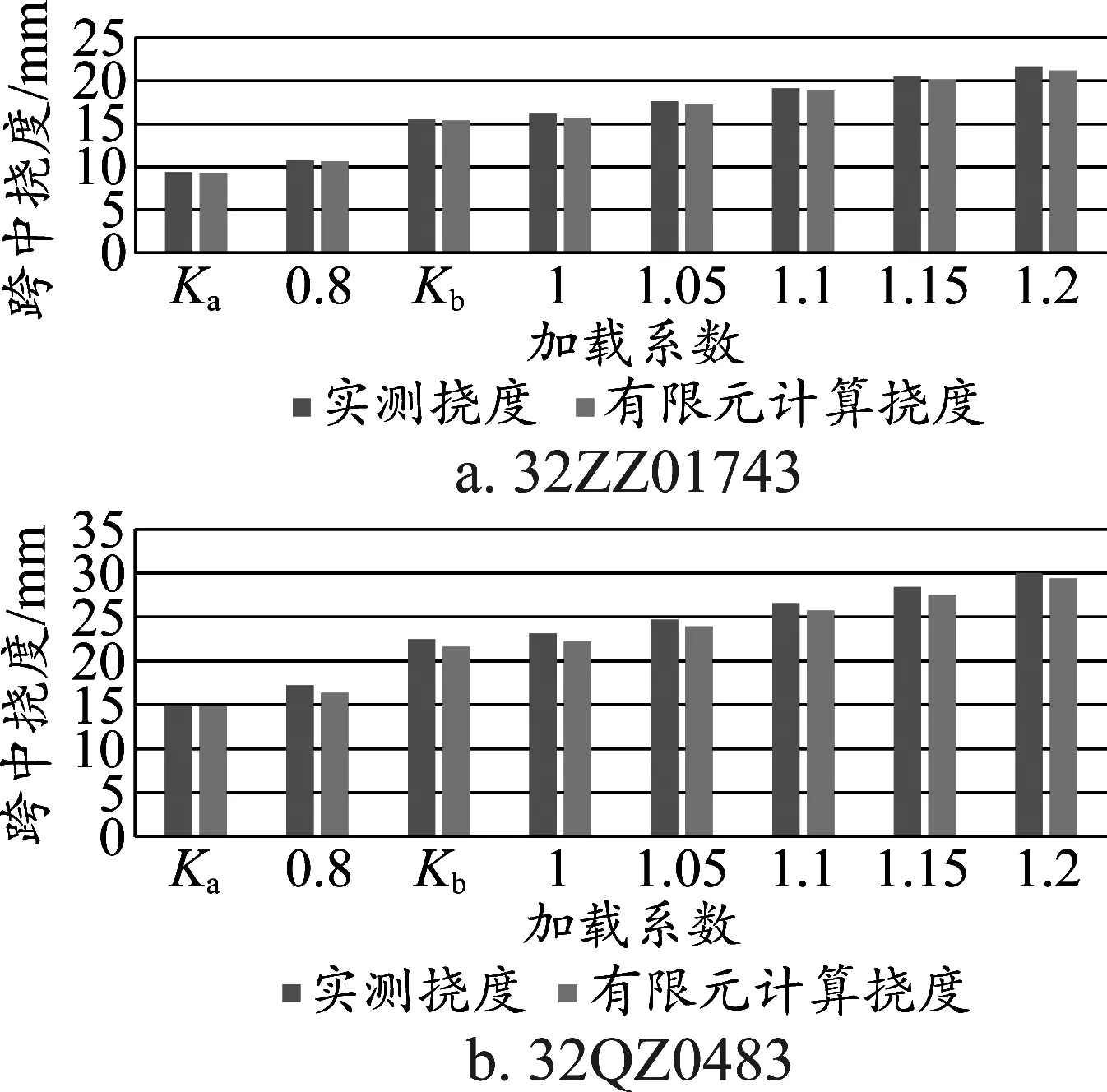
圖9 有限元計算結果與實測結果的對比

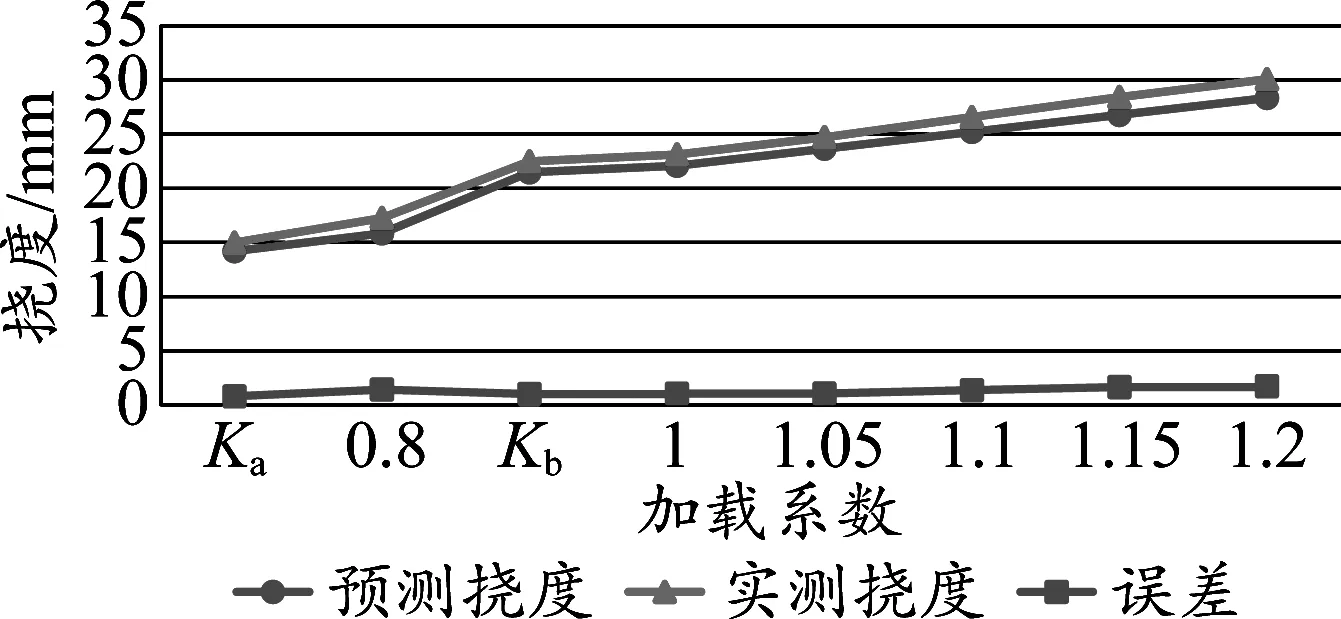
圖10 預測結果與實測結果對比

5.2 結果評定

在Kf＝1.2加載等級下持續20 min，兩片試驗梁梁體下緣底面未發現受力裂紋，兩片試驗梁抗裂性能均合格。實測靜活載撓度值合格評定標準為f實測≤1.05f設計/φ，等效荷載加載撓度修正系數φ取1.040 9，一般以第二加載循環的撓度值作為評定依據。對于32ZZ0174梁，設計撓跨比f設計/L＝1/1 399，實測撓跨比f實測/L＝(fkb-fka)/L＝1/5 087，滿足評定標準；對于32QZ0483梁，設計撓跨比為1/3 682，實測撓跨比為1/4 265，滿足評定要求。兩片試驗梁的剛度均滿足設計要求，剛度富余量在13% ～27%之間。

6 結束語

通過對城際鐵路32 m后張法預應力混凝土簡支T梁的靜載彎曲試驗結果進行分析可得出以下結論:(1)試驗T梁在靜載試驗結束后，其裂縫寬度、剛度、抗裂情況滿足試驗要求；(2)在Ka～1.0階段，兩個加載循環T梁的撓度值基本一致，表明T梁仍處于彈性階段[11-12]；(3)此類T型梁的剛度富余量在13%～27%之間；(4)基于平截面假定和線彈性理論提出了T梁應力分布預測方程和撓度預測方程，由此可以快速推算該型梁在不同荷載下某一點的應力和位移。其研究成果可為此類橋梁的設計與維護提供參考。