合肥市二手房成交價格研究

劉海

摘要：二手房交易市場比重的增大，使得對于二手房房價預測構建模型有重要意義。選取合肥市2019年6月至2020年6月的二手房成交記錄作為研究數據。針對BP神經網絡模型易陷入局部最優和傳統遺傳算法的BP神經網絡收斂速度過慢的不足，建立雙鏈遺傳算法的BP神經網絡模型，對研究數據進行仿真訓練，并檢驗了模型的泛化能力。實驗結果表明使用模型在精度和收斂速度的雙重考量下最優。

Abstract： The increasing proportion of the second-hand housing market makes it important to build a model for the prediction of second-hand housing prices. This paper selects the transaction records of second-hand houses in Hefei City from June 2019 to June 2020 as the research data. The BP neural network model is easy to fall into the local optimum and the convergence speed of the traditional Genetic Algorithm is too slow. In this paper， the BP neural network model of Double-chain Genetic Algorithm is established， the research data are simulated and trained， and the generalization ability of the model is tested. The experimental results show that the proposed model is optimal under the consideration of both accuracy and convergence speed.

關鍵詞：房價預測;BP神經網絡;遺傳算法;雙鏈遺傳算法

Key words： house price forecast;BP neural network;Genetic Algorithm;Double-chain Genetic Algorithm

中圖分類號：F224? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼：A? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文章編號：1006-4311（2020）29-0003-04

0? 引言

近年來中國房地產行業發展迅速，人們買房的需求不斷增加，使得房屋交易由新房交易為主逐步轉變成新房和二手房交易“并駕齊驅”[1]。因此建立模型能夠對二手房房價進行一房一價預測在交易中有重要的參考價值。

在機器學習算法中BP神經網絡由于具有良好的泛化能力、學習能力和映射能力，使得其在房價預測中有一定的優勢[2-4]。然而BP神經網絡在訓練過程容易使模型參數收斂為局部極值，無法達到最優，所以將遺傳算法（GA）與BP神經網絡模型進行組合，補足了神經網絡的缺點[5]。李春生、李霄野[6]等用遺傳算法改進BP神經網絡，對中國2005年至2015年的房價進行研究，發現改進后的算法比單一的BP神經網絡的性能更好。杭曉亞、柳敘豐[7]等運用GA-BP模型對青島市的房價進行預測，效果也十分顯著。但是傳統的遺傳算法存

在收斂過慢或早收斂現象[8]，因此使用雙鏈遺傳算法優化BP神經網絡建立模型對合肥市二手房房價進行預測研究。

1? BP神經網絡和雙鏈遺傳算法

1.1 BP神經網絡

BP神經網絡（Back Propagation Network）是一種通過誤差反向傳播進行參數調優的多層前饋神經網絡，是運用最普遍的神經網絡模型[9]。模型由輸入層、隱含層、輸出層組成，且各層神經元之間采用全連接形式[10]。一個隱含層的BP神經網絡拓撲結構如圖1所示。

BP神經網絡的訓練過程由信號的正向傳播和誤差的反向傳播構成。正向傳播時，信號由輸入層進入網絡，通過隱含層的信號處理后將信號傳入輸出層，當輸出層輸出與期望輸出之間的誤差滿足預設精度則模型訓練終止，否則進入誤差反向傳播階段;反向傳播時，通過梯度下降法優化目標函數將誤差反向傳向各層，對各層每個神經元的權值和閾值進行調整[11]。信號的正向傳播和誤差的反向傳播更替進行，直到誤差精度達到預設要求或者迭代至預設的次數。

1.2 雙鏈遺傳算法

遺傳算法（Genetic Algorithm，GA）是基于達爾文進化論的思想提出的一種優化搜索計算模型，通過模擬自然界物種在繁衍后代過程中個體的選擇、基因的交叉、變異，將優良基因保留而淘汰劣質基因的原則實現對問題解的優化[12]。傳統的遺傳算法在對個體進行編碼時采用的時單鏈染色體結構，本文使用了一種改進算法，引入更符合自然界遺傳規律的雙鏈染色體結構[13-14]，稱之為雙鏈遺傳算法（Double-chain Genetic Algorithm，DGA）。

1.2.1 染色體的雙鏈結構

雙鏈遺傳算法中每個個體有兩條染色體，含有兩份相同的遺傳信息，在進行遺傳操作時通過解鏈只對其中的一條染色體進行交叉、變異產生子代染色體，使得既能參與遺傳進化生成子代基因，又能保留父代潛在的優秀基因，使得迭代進行的遺傳操作時，增加種群的多樣性，擴大了搜索空間[15-16]。

1.2.2 雙鏈染色體遺傳操作

Step1：對需要優化的問題進行編碼處理;

Step2：初始化種群X0，設定最大遺傳代數G，初始遺傳代數g=0;

Step3：計算初始種群個體X0每條鏈適應度值;

Step4：對初始種群中個體進行選擇、交叉、變異操作產生新的個體Xg，此時種群中新個體的雙鏈染色體中既包含父代信息基因鏈也包含子代信息基因鏈;

Step5：計算新個體Xg中父代鏈和子代鏈的適應度值，將適應度值更優的基因鏈代入下一次遺傳操作中，直到g=G時結束。

2? 數據來源及數據預處理

2.1 數據來源

本文使用的數據來自鏈家二手房網（https：//hf.lianjia.com），采集2019年6至2020年6月合肥市二手房成交數據，共得到12581條有效數據。其中每條數據含有特征變量28個，對特征變量進行分類，分為3個類型，分別為數值變量、名義變量和序數變量。具體變量如表1所示。

2.2 原始變量的衍生

在鏈家網上收集到的房屋戶型數據的具體形式有2室1廳1廚1衛、3室1廳1廚2衛等52種形式，若按照處理名義變量的方式來處理此變量，易導致維度災難，因此本文根據房屋戶型變量的數據特征，將其衍生出臥室數量、廚房數量、客廳數量、衛生間數量4個數值變量。

在鏈家網上收集到的梯戶比例數據的具體形式有2梯4戶、1梯2戶、1梯4戶等155種形式，按照處理名義變量的方式來處理也會造成維度災難，因此構造新的梯戶比例：梯數與戶數的比值。

2.3 數據的預處理

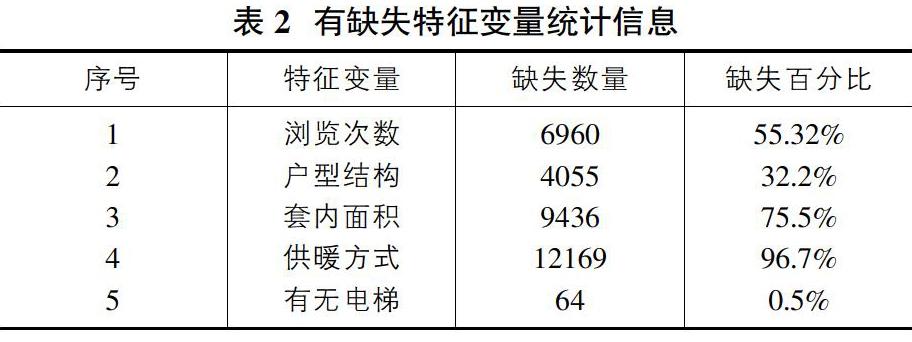
原始數據中可能含有大量的缺失值和異常值，不利于對數據的分析以及后續的建模，為了提升原始數據的質量以便后續工作的進行，需要對數據進行預處理。本文首先對數據的缺失值進行處理，表2展示了有缺失值的特征變量的統計信息。

表2展示了原始數據中部分特征變量的缺失信息。其中瀏覽次數、套內面積、供暖方式缺失比例分別為55.32%、75.5%、96.7%，缺失比例過大，因此將這三個變量直接刪除;有無電梯缺失比例小于1%，因此將缺失的記錄刪除;戶型結構缺失比例為32.2%，采用眾數插補的方式對缺失值進行補充。

對原始數據缺失值進行處理之后在對數據的異常值進行處理，本文通過箱線圖、經驗判斷的方式對異常值進行檢測，并刪除異常值。

2.4 數據量化處理

接著對名義變量和序數變量進行量化處理。其中名義變量采用one-hot編碼處理。

序數變量為所在樓層，取值為低、中、高，可分別取值為0、1、2。

為消除數值變量量綱的影響，將數值變量進行歸一化，歸一化的公式為：

其中xstd為歸一化后的數據，xmin和xmax分別為每個數值變量的最小值與最大值。

至此完成對數據的處理，下面將處理后的數據用于建模。

3? DGA-BP二手房成交價格預測模型

3.1 DGA-BP模型參數設置

DGA-BP模型設置的參數分為BP神經網絡參數設置和雙鏈遺傳算法參數設置，設置具體如下：

①確定BP神經網絡模型的基本結構。確定BP神經網絡的隱含層層數及各層神經元個數。設定神經網絡輸入層有54個神經元，1個隱含層且隱含層神經元有109，輸入層有1神經元。同時通過多次調整確定BP神經網絡的學習率為0.01，預設迭代次數為30000次。

②設定適應度函數，用于計算種群中個體的適應度。本文使用測試集誤差本文使用BP神經網絡測試集的測試誤差作為適應度函數，適應度函數為：

yi為測試集中數據的真實值，i為數據的估計值。

③設定最大遺傳代數，初始化種群，隨機產生一個初始種群，將種群中每個個體通過格雷編碼的方式進行編碼，每個個體含有兩條信息相同的染色體，都含有神經網絡權值和閾值的全部信息，并計算初始種群中每個個體的每條鏈的適應度值。本文設定種群規模為50，最大遺傳代數為200。

④進行遺傳操作設定：

選擇算子：本文采用輪盤賭的方式進行選擇操作;

交叉算子：本文采用兩點交叉的方式進行交叉操作;

變異操作：本文設定的變異概率為0.01。

3.2 模型評價指標

①平均絕對誤差（MAE）。平均絕對誤差是期望值與預測值差值的平均值。計算公式如下：

其中n為樣本數目，yi為期望值，i為估計值。

②均方誤差（MSE）。均方誤差是期望值與預測值差值平方的平均值。計算公式為：

其中n為樣本數目，yi為期望值，i為估計值。

③可決系數（R2）。可決系數是判定模型擬合能力的指標，可決系數越大則模型的擬合能力越強。其計算公式如下：

式中：SSE為回歸平方和;SST為總離差平方和;SSR為殘差平方和，其計算公式如下：

其中yi為樣本的期望值，yi為樣本的平均值，i為樣本的估計值。

3.3 實驗結果

本文使用有效數據9817條數據，按照3：7的比例將數據集劃分為測試集與訓練集，通過與BP神經網絡和傳統的GA-BP模型進行比較，突出本文使用的DGA-BP模型的優越性。

其中圖2表示DGA-BP模型在收斂速度上與GA-BP模型的比較結果。從圖中可以看出DGA-BP模型的收斂速度遠遠快于GA-BP模型，在進化到53代時就達到最佳收斂，收斂速度遠遠快于GA-BP模型。

表3表示了BP模型、GA-BP模型、DGA-BP模型在測試集上的計算結果的展示，從表中可以看出在MAE、MSE、R2指標的測度中，GA-BP模型和DGA-BP模型的計算結果都優于BP模型。

從上述敘述中可以總結得出DGA-BP模型在收斂速度和算法精度的綜合考量中最優，于此同時新抓取了合肥市二手房成交數據800條，使用DGA-BP模型進行擬合，得出其MAE為784、MSE為787652、R2為0.9123。其前100個數據擬合結果展示如圖3所示，通過新抓取數據的驗證，可以看出DGA-BP模型能夠對合肥市二手房成交價格進行較好的預測。

4? 結論

本文通過采集合肥市2019年6月至2020年6月城區二手房成交記錄數據，對比傳統BP神經網絡模型和GA-BP模型，建立一種能夠對二手房成交價格進行有效預測的DGA-BP模型，該模型彌補了BP模型和GA-BP模型的不足，使得在追求模型收斂速度和預測精度的雙重考量為最優選擇。在進化到54代時，對測試集進行擬合，可決系數R2為0.9406，對新抓取數據的擬合，可決系數為0.9123。說明模型有較好的泛化能力。

然而在建模時將搜索到的所有指標都投入模型中，沒有考察變量的有效性從而對指標進行篩選，使得本文建立的模型未能最簡化，也降低了模型的收斂速度。今后對如何在眾多指標中篩選中穩健的重要指標是研究的一個方向點。

參考文獻：

[1]姜沛言，孫聰，劉洪玉.住房市場研究中的樣本城市選擇[J].統計與決策，2016（05）：29-33.

[2]李廣勝，郭歡.基于GM（1，1）模型的南京市房價預測研究[J].江漢大學學報（自然科學版），2020，48（02）：10-13.

[3]高文，李富星，牛永潔.基于BP神經網絡對房價預測的研究[J].延安大學學報（自然科學版），2018，37（03）：37-40.

[4]王筱欣，高攀.基于BP神經網絡的重慶市房價驗證與預測[J].重慶理工大學學報（社會科學），2016，30（09）：49-53.

[5]張立毅，劉婷，孫云山，李鏘.遺傳算法優化神經網絡權值盲均衡算法的研究[J].計算機工程與應用，2009，45（11）：162-164.

[6]李春生，李霄野，張可佳.基于遺傳算法改進的BP神經網絡房價預測分析[J].計算機技術與發展，2018，28（08）：144-147，151.

[7]杭曉亞，柳敘豐，趙澤昆.基于GA-BP神經網絡的青島房價預測[J].四川建筑，2015，35（06）：233-236.

[8]PHOLDEE N， BUREERAT， S. Hybrid real-code population-based incremental learning and approximate gradients for multi-objective truss design[J]. Engineering Optimization， 2014， 46（8）：1032-1051.

[9]李英冰，陳雨勁，歐陽茜.基于BP神經網絡的武漢市二手房估價模型研究[J].數字制造科學，2017，15（Z1）：66-70.

[10]嚴旭，李思源，張征.基于遺傳算法的BP神經網絡在城市用水量預測中的應用[J].計算機科學，2016，43（S2）：547-550.

[11]任謝楠.基于遺傳算法的BP神經網絡的優化研究及MATLAB仿真[D].天津師范大學，2014.

[12]李巖，袁弘宇，于佳喬，張更偉，劉克平.遺傳算法在優化問題中的應用綜述[J].山東工業技術，2019（12）：242-243，180.

[13]劉金山，廖文和，郭宇.基于雙鏈遺傳算法的網絡化制造資源優化配置[J].機械工程學報，2008（02）：189-195.

[14]Harsh Bhasin， Gitanshu Behal， Nimish Aggarwal， Raj Kumar Saini， Shivani Choudhary. On the applicability of diploid genetic algorithms in dynamic environments[J]. Soft Computing， 2016， 20（9）.

[15]吳家宏，雷毅.基于雙螺旋染色體和分層結構的遺傳算法[J].計算機集成制造系統，2005（12）：1743-1746.

[16]謝承旺，王志杰，魏波，徐君，汪慎文.一種雙鏈結構的多目標進化算法DCMOEA[J].控制與決策，2015，30（04）：577-584.