船體形狀因子的數值分析

艾子濤，徐方磊，周廣利

(1.中國船級社廣州分社 廣州審圖中心，廣州 510235；2.哈爾濱工程大學 船舶工程學院，哈爾濱 150001)

船模阻力試驗是長期以來預報實船阻力最常用的方法之一[1-2]。在對試驗結果換算過程中會涉及到船體形狀因子(1+k)，它對換算預報結果有重要影響[3-4]，一般可通過低速模型試驗獲得，此時興波很小甚至趨近于零。現代船舶一般具有球艏或同時具有方艉，船模在低速試驗過程中難免產生興波，同時，受限于實驗儀器設備條件，低速狀態下的模型阻力不易測準。因此，通過模型試驗方法獲得精確可靠的船體形狀因子(1+k)較為困難。

隨著計算機軟硬件技術的飛速發展，計算流體力學(CFD)技術在船舶水動力性能預報中發揮著越來越重要的作用[5-10]。其中的疊模方即為將水下部分船體以水線面作為對稱面進行對稱而形成兩個船模疊扣在一起的形式，進而將此形式的船模完全置于水下進行拖曳的方法。該方法免去了興波阻力的干擾，此時的總阻力即為黏性阻力。然而該方法在試驗中實現困難，應用CFD技術計算該方法下的黏性阻力，不但可以避免在物理模型試驗中普遍存在的系統誤差和偶然誤差，還可精確地設定和控制各方向的來流速度，并達到通過疊模數值計算獲得黏性阻力、分離出摩擦阻力和黏壓阻力、得到船體形狀因子(1+k)的目的。

本文選取KCS等3種船型，采用CFD商用軟件對其進行疊模低速阻力計算，并將獲得的船體形狀因子(1+k)分別與通過低速物理船模阻力試驗結合普魯哈斯卡(Prohaska)法、ITTC推薦方法計算得到的船體形狀因子進行對比分析，探討通過CFD疊模計算船體形狀因子(1+k)的可靠性。

1 船體形狀因子1+k

1.1 1+k原理

為了達到由一定縮尺比的船模試驗來預估實船阻力的目的，通常需要選擇換算方法。常用的換算方法有二因次換算法(又稱弗勞德換算法)和三因次換算法(又稱1+k法)。二因次法基于弗勞德假設，其內容為：①船體總阻力可以劃分為摩擦阻力和剩余阻力2部分，二者是相互獨立的，摩擦阻力只與雷諾數有關，剩余阻力僅與弗勞德數有關，包含黏壓阻力和興波阻力；②船體摩擦阻力可以用相同速度、相同長度、相等濕表面積的相當平板摩擦阻力代替。這樣，船體總阻力可以表示為Rt(Re，Fr)=Rf(Re)+Rr(Fr)。

弗勞德假設將不同性質的黏壓阻力和興波阻力合并在一起，稱為剩余阻力，并認為適用比較定律，這在理論上是不妥當的[11]。為了在一定程度上克服用相當平板濕面積的摩擦阻力系數或相關線公式的不合理性，同時考慮到船體三維形狀與平板的差異所產生的對黏性阻力的影響，休斯提了三因次方法：即船體總阻力可劃分為黏性阻力和興波阻力2種成分，而黏性阻力則可以有相當平板阻力摩擦并考慮到船體三維形狀加以修正得到。Ctm=(1+k)Cfm+Crm，式中引入以系數k，稱為船體形狀系數，并認為k是常量，將同一個k值用于各個速度下的阻力換算，以及用于實船；即在船模(m)和實船(s)總阻系數中分別加上形狀阻力系數kCfm和kCfs，另再加上反映粗糙度和某些其他因素引起的阻力成分——換算補貼，連同空氣阻力系數等，獲得外插的實船總阻力系數。

1.2 通過模型試驗獲取1+k的方法

傳統的基于低速船模試驗結果確定船體形狀因子(1+k)的方法主要有普魯哈斯卡(Prohaska) 法和ITTC推薦方法。以上2種方法均假定Fr=0.1～0.2范圍內，船體興波阻力系數Cw與Fr的m次方成正比，其中Cw=yFrm，總阻力系數表達式為

Ct=(1+k)Cf+yFrm

(1)

將式(1)的兩邊同時除以Cf可得

Ct/Cf=(1+k)+yFrm/Cf

(2)

令Y=Ct/Cf，X=Frm/Cf，b=1+k即有

Y=yX+b

(3)

通過具體的模型試驗點數據可以構造一組(Xi，Yi)，i=1,2,…,n，采用最小二乘法進行線性擬合即可求得對應的參數y，b。

構造誤差函數:

(4)

使誤差函數為最小值的y、b即為所求，令誤差函數E(y,b)對y和b的偏導數為0,整理可得

(5)

若選用Prohaska方法對模型試驗數據進行處理，則取m=4。根據式(1)～(3)代入試驗點數據，通過線性擬合得到直線在縱坐標抽上的截距就是船體形狀因子1+k。若選用ITTC推薦方法，則m的取值范圍為2～6，可先假定一系列的m值進行計算，其中使誤差函數值最小的一組參數即為所求。

1.3 CFD疊模計算獲取1+k的方法

由休斯提出的三因次換算方法的主要觀點是將黏壓阻力與摩擦阻力合并為黏性阻力。這樣船體總阻力可以劃分為與雷諾數相關的黏性阻力和與弗勞德數相關的興波阻力2種成分，即

Ct=Cv(Re)+Cw(Fr)

(6)

并且認為黏性阻力系數Cv與摩擦阻力系數Cf之比為一常數，即船體形狀系數k。

k=Cpv/Cf或者1+k=Cv/Cf

(7)

由于在CFD疊模計算過程中沒有自由液面的影響，計算獲得的船體總阻力中沒有興波阻力而只有黏性阻力，這樣通過數值模擬計算得到的黏性阻力和基于相當平板理論計算得到的摩擦阻力即可直接求得船體形狀因子1+k。

2 CFD計算

選取KCS船、散貨船、高速單體船3種比較典型的船型，建立三維曲面模型，進行網格劃分和阻力計算。

網格劃分對數值計算結果影響很大。根據ITTC的推薦及此前的研究[12]，對船體表面設置hull far、hull near、hull 3個加密區；將y+值選取為100～200；邊界層數選取6；模型船體表面第一層網格厚度約為2 mm。最終KCS船、散貨船、高速單體船生成網格數分別為340萬、380萬和300萬。

疊模阻力計算采用的是雙對稱模型，以船模縱舯剖面和靜水面作為對稱面，求解計算域。流體計算域選用比較常用的尺寸：在船長方向上，從船艏向前延長1個船長，從船艉向后延伸3個船長；在船寬方向上，從主體中縱剖線向兩側各延伸1.5個船長；在高度方向上，從船底向下延伸1個船長。計算域設置分為速度入口邊界、壓力出口邊界，TOP面設為對稱面邊界，其它邊界均設為無滑移固壁邊界；船體正浮并且航態固定；流域內為不可壓縮流體，其運動滿足連續性方程和動量守恒定律；湍流模擬方法應用Reynolds 平均法，湍流模式采用Realizablek-ε模型[13]。

3 計算方案

3.1 KCS船型

該計算模型針對的是一艘KRISO的3 600 TEU集裝箱船，標準船模的相關參數、幾何模型分別見表1，圖1。

表1 KCS船模型參數

圖1 KCS船模型

數值計算的模型速度為Vm=0.7、0.8、0.9、1、1.1、1.2、1.3 m/s，對應的量綱一的量化航速為Fr=0.107、0.122、0.138、0.153、0.168、0.183、0.199。疊模計算結果和壓力云圖(Fr=0.199)分別見表2，圖5。Rf，Rv分別為船體的摩擦阻力和總的黏性阻力。

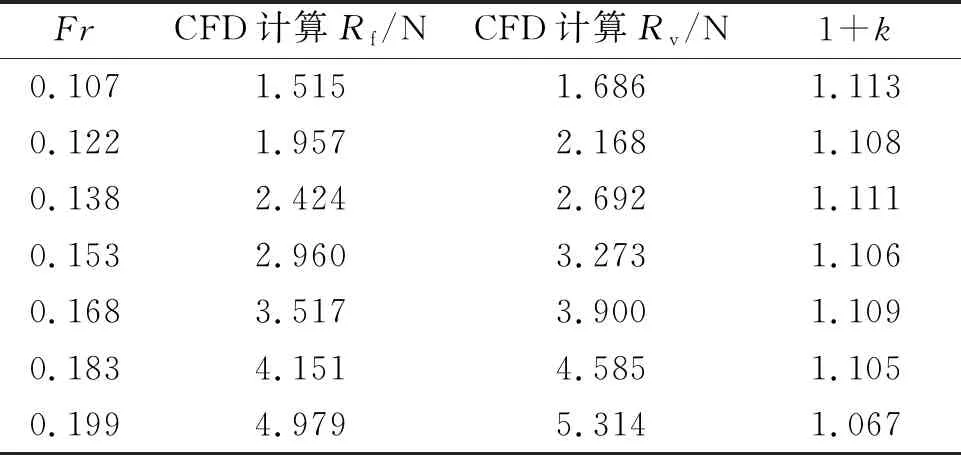
表2 KCS船體形狀因子1+k計算結果

將按照式(1)～(4)計算的結果繪于圖2、3。

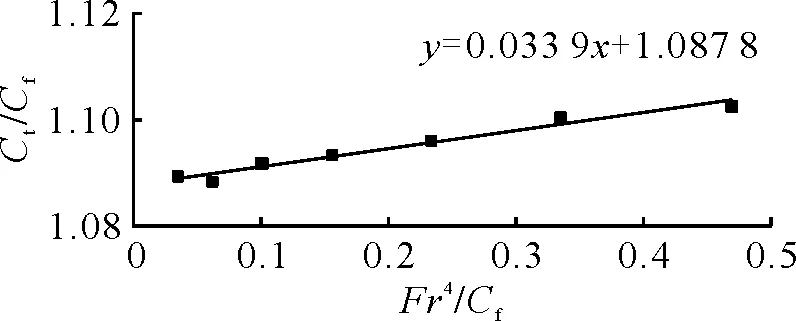
圖2 KCS普魯哈斯卡法(1+k)線性擬合結果

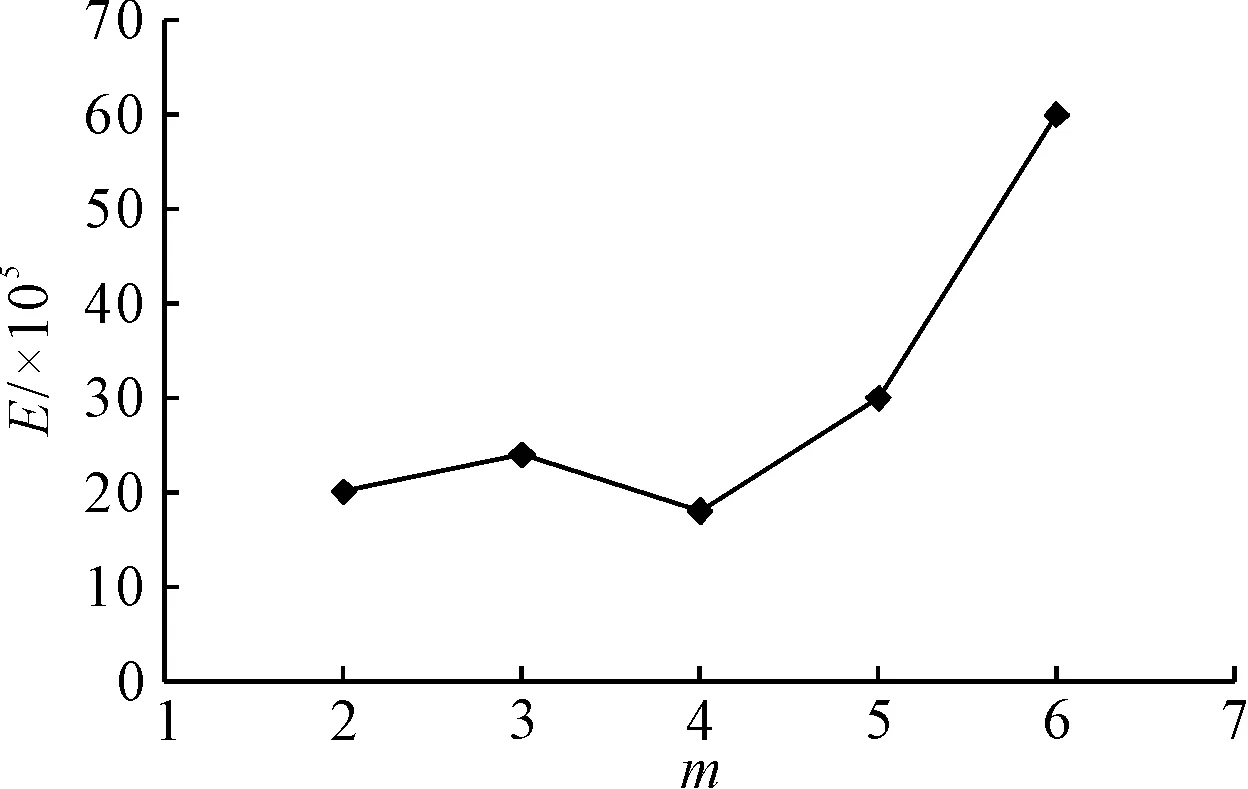
圖3 KCS ITTC建議方法線性擬合誤差隨m的變化

表2為通過數值模擬計算得到的不同弗勞德數下的1+k值。由表2可見，在不同Fr下船體形狀因子的1+k的值略有不同，但變化范圍不大，上述7個Fr下1+k的平均值為1.103。由圖2可知,根據模型試驗數據采用Prohaska法計算得到的船體形狀因子為1.088。由圖3可知，當取m=4時誤差函數E值最小，ITTC推薦方法求得的船體形狀因子與Prohaska法相同，均為1.088。經比較可得：通過CFD疊模計算得到的船體形狀因子(1+k)與Prohaska法及ITTC推薦方法得到的結果相比相差1.2%。

圖4為Fr=0.199時，水線以下3 cm平面和船體表面的來流方向壓力分布情況。

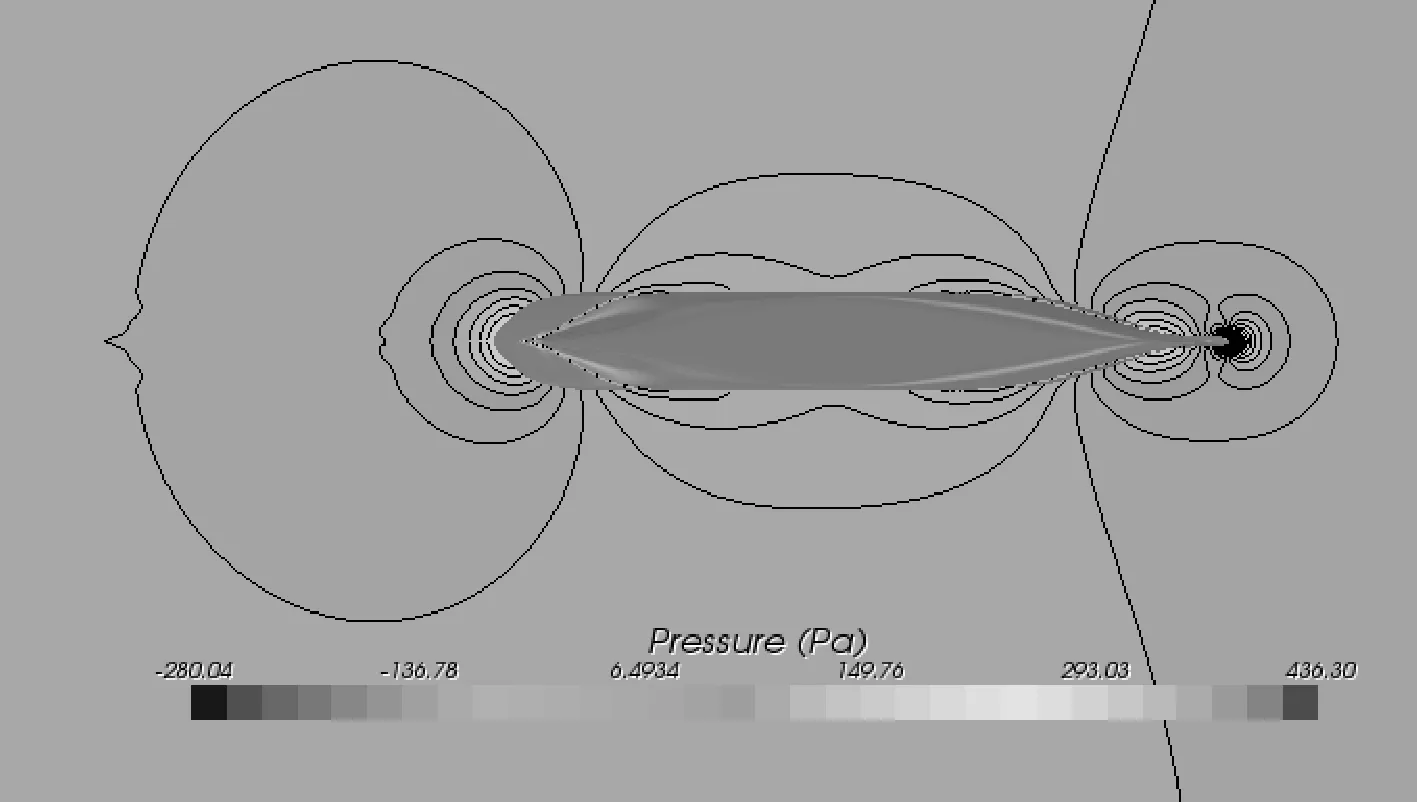
圖4 KCS船壓力分布云圖(Fr=0.199)

由圖4及數值計算得到的壓力值表明，高壓區域位于船艏、艉部，低壓區域則位于船體舯部范圍內，且分布十分規律。

3.2 散貨船

該計算模型針對的是某35 000 DWT散貨船，數值模擬計算采取與前述KCS船相同的網格劃分及計算方式。船模的相關參數、幾何模型分別見表3、圖5。

表3 散貨船船模型參數

圖5 散貨船模型

數值計算中的模型速度為Vm=0.75、0.85、1、1.15、1.3、1.45 m/s，對應的無量綱化航速為Fr=0.102、0.116、0.136、0.157、0.177、0.198。疊模計算結果和壓力云圖(Fr=0.198)分別見表4，圖8。Rf，Rv分別為船體的摩擦阻力和總的黏性阻力。

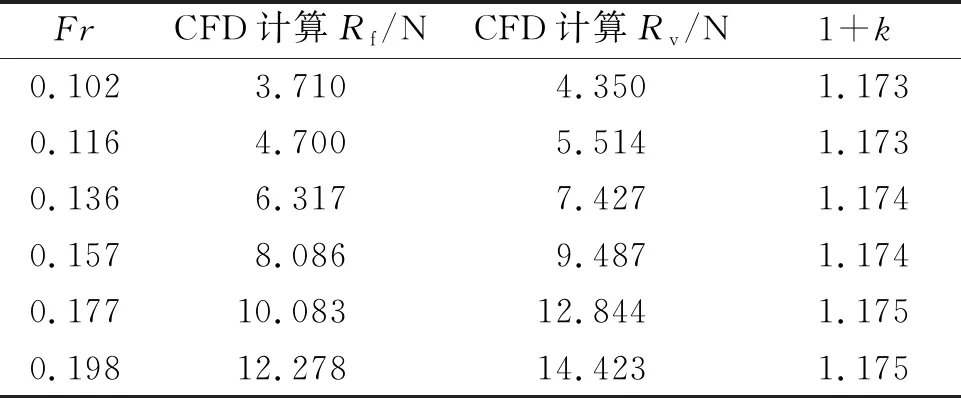
表4 散貨船船模1+k計算結果

表4中給出的通過疊合模數值模擬計算得到的6個Fr下船體形狀因子1+k的平均值為1.174，利用低速船模阻力試驗結果采用Prohaska法和ITTC推薦方法計算得到的船體形狀因子(1+k)則分別為1.196、1.197(m=5時求得)，相差分別為1.83%、1.92%。從圖8中亦可看出, 沿船長分布的高壓區域位于艏、艉部，低壓區域則位于船體舯部范圍內，且分布較為規律,無壓力突變的區域。

圖6 散貨船普魯哈斯卡法(1+k)線性擬合結果

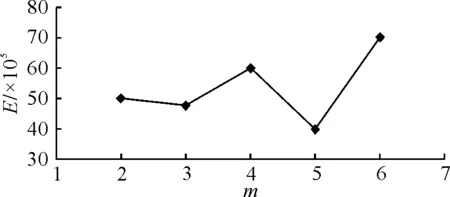
圖7 散貨船ITTC推薦方法線性擬合誤差隨m的變化

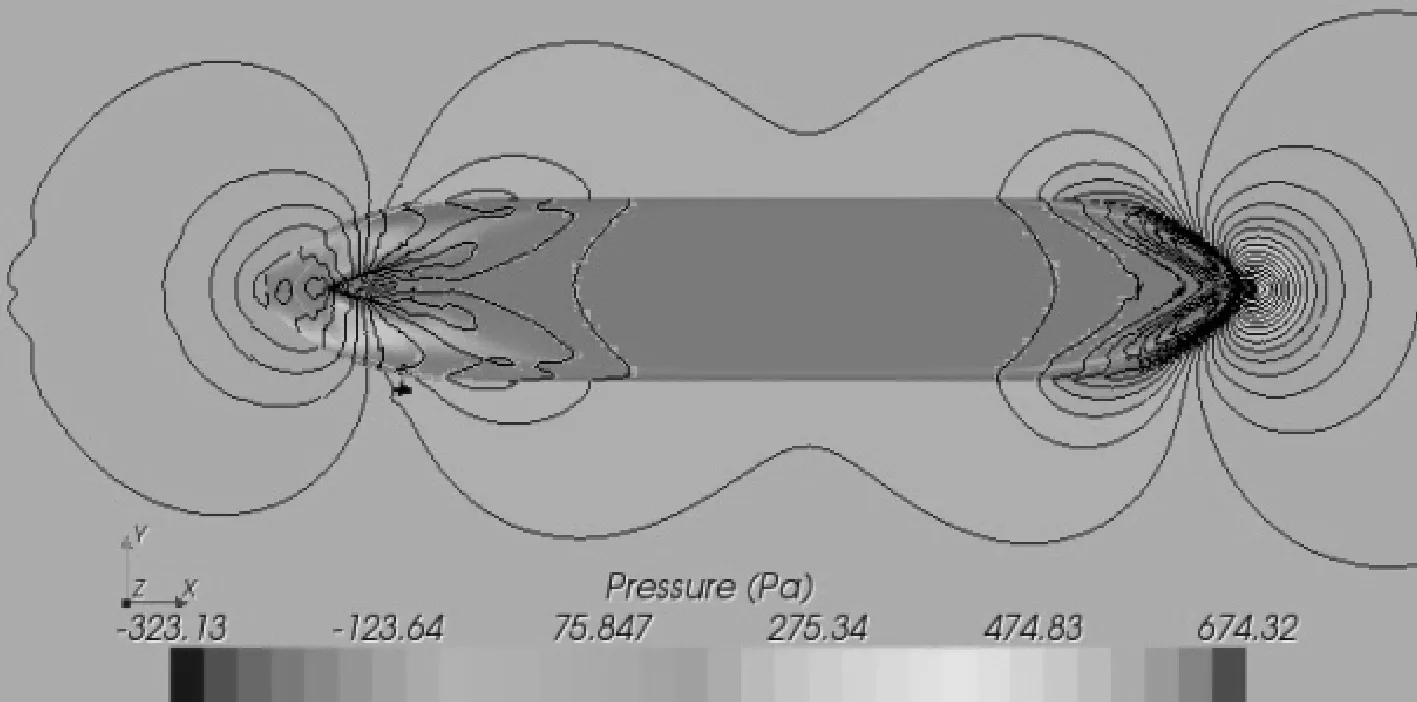
圖8 散貨船壓力分布云圖(Fr=0.198)

3.3 某高速單體船

計算模型取自某高速單體船，亦采取與KCS船相同的網格劃分及計算方式。船模的相關參數、幾何模型分別見表5，圖9。

表5 某高速單體船模型參數

圖9 高速船模型

數值計算中的模型速度為Vm=0.6、0.7、0.8、0.9、1 m/s，對應的量綱一的量化航速為Fr=0.111、0.129、0.147、0.166、0.184。疊模計算結果和壓力云圖(Fr=0.184)分別見表6，圖12。Rf，Rv分別為船體的摩擦阻力和總的黏性阻力。

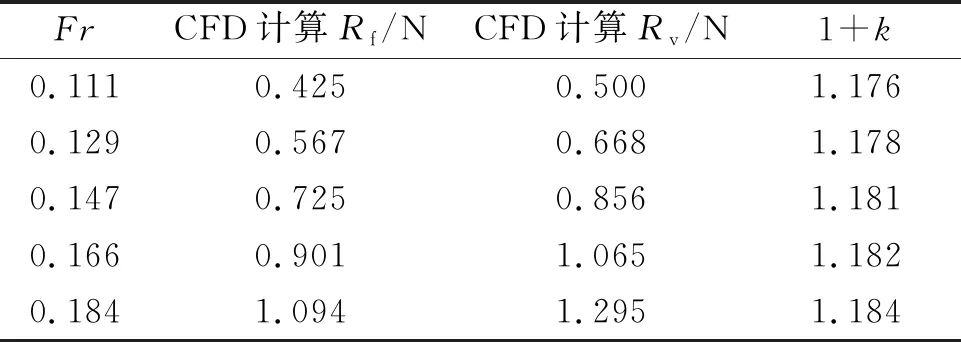
表6 高速船1+k計算結果

圖10 高速船普魯哈斯卡法(1+k)線性擬合結果

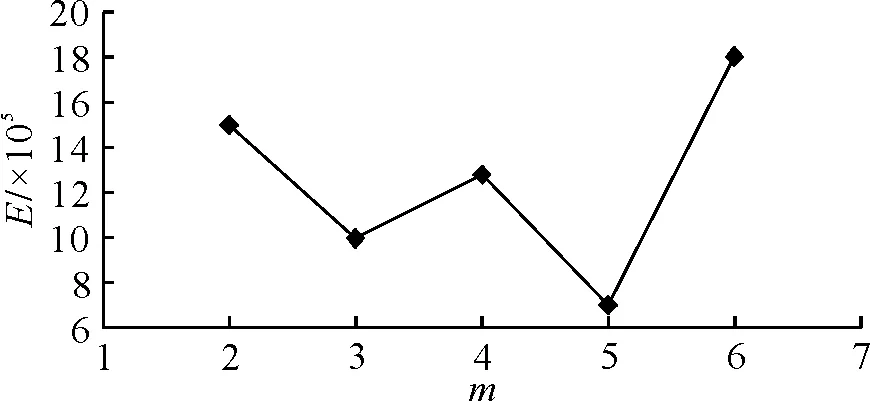
圖11 高速船ITTC推薦方法線性擬合誤差隨m的變化

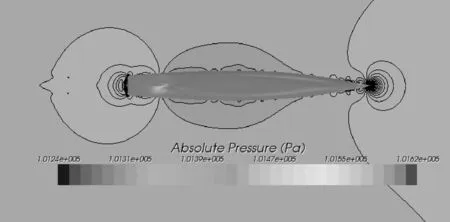
圖12 高速船壓力分布云圖(Fr=0.184)

表6中5個Fr下1+k的平均值為1.18，采用Prohaska法和ITTC推薦方法計算可得(1+k)分別為1.166、1.168(m=5時求得)，相差分別為1.4%、1.02%。由圖12可見,高壓和低壓區域與上述KCS和散貨船類似,但沿船長壓力改變區域較小且在船艏艉及舯部有若干小的突變區域,這主要是由于船體比較瘦長,長寬比較大。

4 結論

1)采用CFD疊模計算方法得到的船舶低速航行時摩擦阻力結果與理論計算值較為吻合，表明利用CFD疊模法計算摩擦阻力以及船體形狀因子(1+k)具有一定的可行性，可為高速下的船體形狀因子(1+k)的計算提供計算基礎。

2)從壓力云圖可以看出，沿船長方向高壓區域位于船艏、艉部，低壓區域則位于船體舯部范圍內，各區域壓力分布的較為均勻，無較大壓力突變的地方，從最終結果來看，疊模計算船體形狀因子(1+k)與理論計算及物理模型試驗也十分貼近。

3)針對KCS船型、散貨船、高速單體船而言，基于CFD疊模計算的船體形狀因子與模型試驗測得形狀因子十分接近，具有較高的工程應用價值。但本文進行計算和驗證的船型有限，對于其他船型(比如多體船等)有待后續研究。