高等數學中數列極限的求解方法

梁新峰，任丹丹

（安徽理工大學數學與大數據學院，安徽淮南232001）

數列是大學高等數學、數學分析及數學專業相關專業課程的基本知識點。它在大學的數學學習過程中起到了重要的作用。通過對數學分析和高等數學等課程的分析可知，數列極限不僅與函數極限密切相關，而且為學習定積分的定義、級數理論及離散數學等提供了極為重要的準備知識。另外，在“新工科”的背景下，我們秉承“傳道授業解惑”的宗旨，樹立和明確研究目標，更加注重對數列求解的方法創新及其對方法的分類。鑒于此，我們著重研究數列極限的求解方法及其分類。

函數是由定義域、對應法則及其值域所決定的，而數列是一類以正整數集（或者它的子列）為定義域的特殊函數。鑒于此，我們可以從函數的角度研究數列的結構性質。數列根據其不同的結構性質可分為有窮數列和無窮數列、周期數列、常數列等。因此，我們可以依據數列自身的結構性質采用不同的求解方法。

下面我們對數列收斂性的求解方法進行系統的研究。

1 數學歸納法

數學歸納法是一種基礎的數學證明方法，通常用于證明與自然數N有關的命題成立，它主要用來研究與正整數有關的數學問題。故我們可以利用數學歸納法證明和求解某些特定數列的極限。解題過程通常分為兩步，首先通過數學歸納法證明數列的極限是存在的，在此基礎上，利用等式兩端同時取極限、求解方程等方法求解數列的極限。

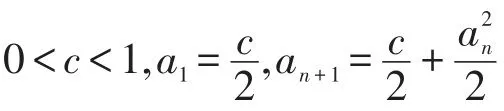
2 變量替換法

當已知兩個數列中某些項之間的關系式時，直接證明兩個極限均收斂往往是比較困難的。我們常常需要依據原有的關系式選取合適的中間變量，將原有的關系式化簡，以便證明極限收斂。這樣既可以簡化我們的計算過程，又可以降低我們的解題難度。

3 函數極限法

數列是一種以正整數或者其子列為定義域的特殊函數。對于特定的較為復雜的數列，我們依據數列自身的結構及其關系式難以直接得到其極限。鑒于數列和函數之間的特殊關系，結合子列的收斂性和數列的收斂性的關系，我們可以將間斷的數列的極限轉化為對應連續函數的極限進行研究探討。

4 定積分法

定積分是高等數學和數學分析等課程中重要的知識點，其在求解圖形面積和物體質量等現實問題中起到了至關重要的作用。我們注意到定積分的定義是通過“分割、近似、求和及取極限”等4個步驟給出的。在此過程中，取極限是至關重要的一步，此步將煩瑣的求極限的過程轉化為定積分的求解過程。

5 利用微分中值定理法

在方法3中，我們注意到函數和數列之間的關系，如果數列對應的函數在特定的閉區間內是連續且可導的，則我們可以利用連續函數在閉區間內的結構性質（如拉格朗日中值定理、柯西中值定理等）研究數列的結構性質。下面我們利用函數的微分中值定理將例1重新證明，以此說明此法在研究數列收斂中的作用。

6 利用施篤茲公式進行求解

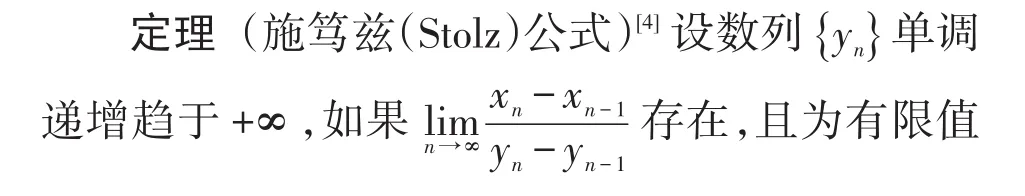
6 結束語

本文闡述了數列在大學數學學習中的重要性，并基于此，對研究數列收斂的方法進行了較為全面的分類和闡釋，包括數學歸納法、變量代換法、積分法、利用微分中值定理和施篤茲（Stolz）公式等。