基于改進LFMCW雷達的多目標識別算法

鄒麗蓉，朱 莉，邵文浩

(南京理工大學電光學院探測與控制工程系，江蘇南京210094)

0 引言

線性調頻連續波(Linear Frequency Modulated Continuous Wave，LFMCW)雷達[1]測距具有無距離盲區、高距離分辨率和低發射功率等優點，廣泛應用于軍事領域，近年來，也逐漸運用于民用領域，如汽車防撞雷達[2]等。

LFMCW雷達在單目標情況下可以根據上下掃頻段的兩個差頻信號準確地測得目標的距離信息及其徑向速度。在多目標情況下，上下掃頻段的差頻信號，由于缺乏關聯信息無法準確配對，產生的虛假目標數目遠大于真實目標數目。針對上述問題，多篇文獻提出解決方案。文獻[3]提出一種采用變周期LFMCW的多目標識別方法，通過發射3組不同掃頻周期的三角波調頻信號來識別虛假目標。該方法能夠有效剔除絕大部分虛假目標，但存在計算量大、掃頻周期長、占用資源多等缺點，且產生不同掃頻周期的信號加大了硬件實現的難度。文獻[4]提出了一種將定頻信號與三角波調頻信號相結合的多目標識別方法，由定頻信號可以得到運動目標的速度信息，可將此作為剔除虛假目標的依據，該方法計算量小且波形容易實現，然而當虛假目標與真實目標速度相同且無法利用假設法正確配對時，仍然無法識別。文獻[5]結合文獻[3]與文獻[4]所提出的方法，將變周期三角波的第一段改為定頻信號，第二第三段保持不變，利用定頻信號得到的速度信息可以直接剔除一些虛假目標，對剩下的疑似真實目標點進行進一步的計算，在一定程度上減少了計算量，變周期也能有效剔除虛假目標。但是該方法依然要發送2組不同掃頻周期的三角波調頻信號，硬件實現仍有難度。

為準確識別真實目標，本文提出一種改進LFMCW波形，在LFMCW波形前加上兩段頻率值互異的恒頻波段，兩段恒頻波段組成雙頻調制連續波(Frequency-Shift Keying Continuous Wave，FSK-CW)[6]，可得到運動目標的距離信息及其徑向速度用于剔除虛假目標。該波形計算量小，硬件易實現，且能有效識別真實目標。

1 LFMCW波形

LFMCW信號是頻率作周期性變化的一種信號，收發信號產生的時間差可以通過頻率的差異顯現出來，該波形因其易檢測性廣泛應用于雷達系統中。當調制波形為鋸齒波時，動目標情況下會產生速度距離耦合[7]，無法得到目標正確的距離與速度信息，而三角波調制可以將速度距離解耦合，因此本文選擇三角波作為頻率調制波形。

將收發信號進行混頻后再低通濾波得到的信號稱為差頻信號，差頻信號直接反映了收發信號的頻率差。三角波調頻信號的時間-頻率曲線和收發信號的差頻信號如圖1所示。由圖1可以看出，在三角波的上掃頻段和下掃頻段分別會產生一段恒頻段，通過分析這兩個恒頻信號可以得到目標的距離信息和徑向速度。

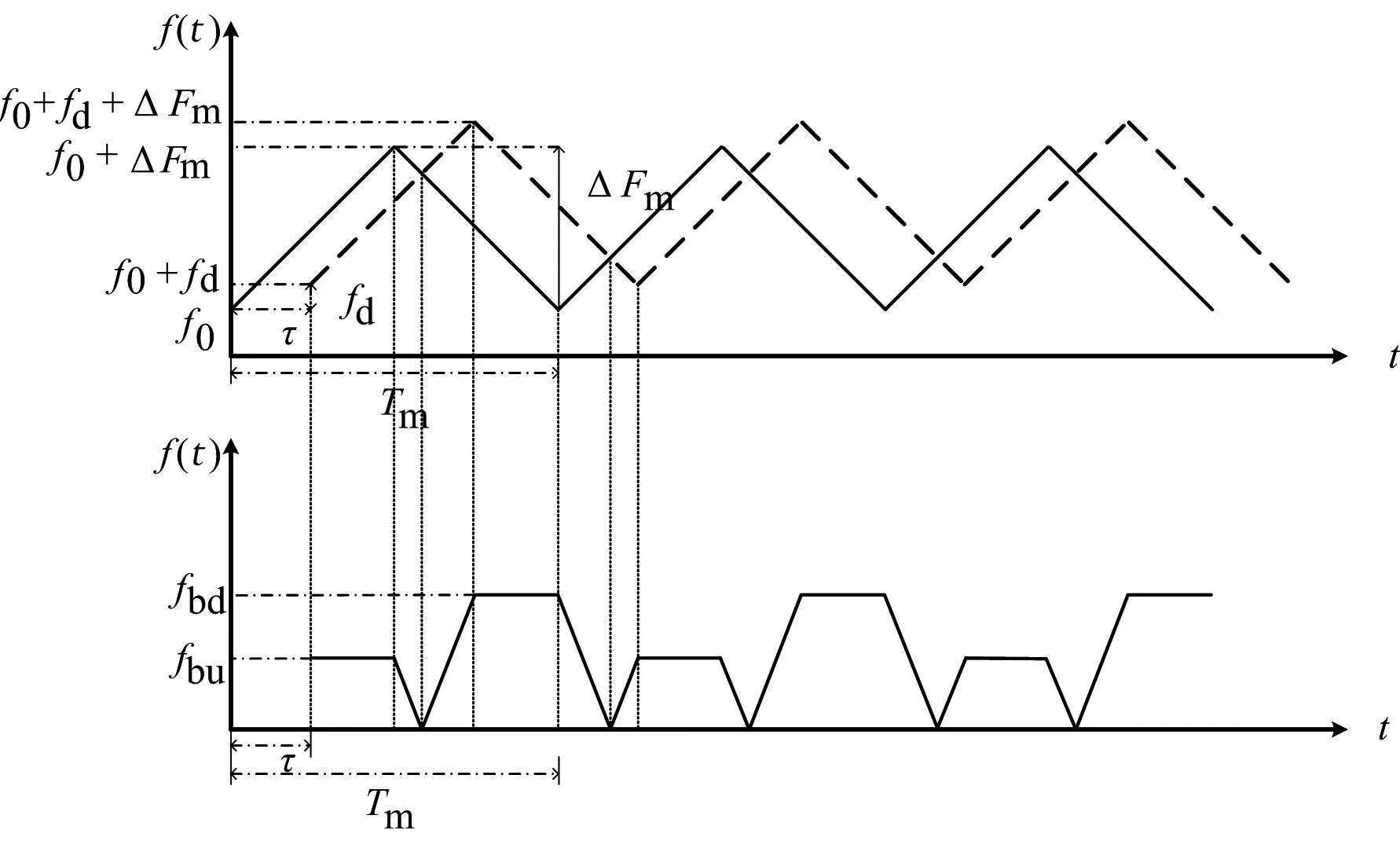
圖1 三角波調頻信號的時間-頻率曲線和收發信號的差頻信號

不妨設發射信號sT(t)是初相為φ0的單位正弦信號，在上掃頻段，其頻率為f=f0+kt，式中k=2ΔFm/Tm為調頻斜率，ΔFm為最大頻偏，Tm為調制周期。sT(t)的完整表達式為

(1)

經過延時τ，接收機接收到回波信號sR(t)，τ的表達式為τ=2(R+vt)/c，式中R為信號發射時刻目標與雷達的距離，v為目標與雷達連線方向的速度，目標遠離雷達為正，c為光速。sR(t)的完整表達式為

sR(t)=Krsin{2π[f0(t-τ)+

(2)

式中，Kr為信號反射和傳播引起的衰減因子，φ0為信號反射引起的額外相位差[4]。將發射信號與接收信號進行混頻，經數學推導混頻信號可化簡為

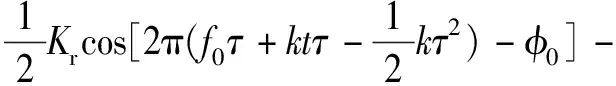
(3)

經過低通濾波濾除高頻分量，得到收發信號的差頻信號sbu(t)為

(4)

將τ=2(R+vt)/c代入式(4)，化簡得

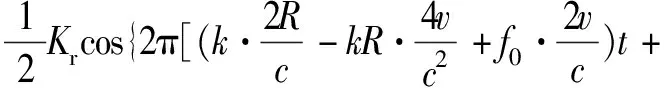
(5)

考慮到v?c，v/c2項都可以忽略不計，此時差頻信號sbu(t)可簡化為

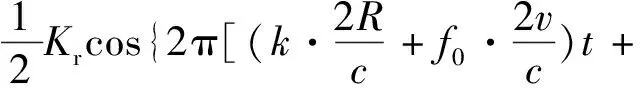
(6)

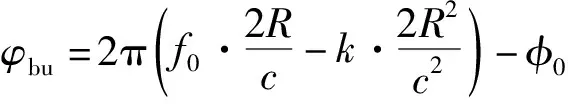
(7)

式中，fb是目標速度為零時收發信號的差頻信號，fd是運動目標的多普勒頻移。同理可得，在下掃頻段，收發信號的差頻信號sbd(t)的頻率fbd為

(8)

由于ΔFm的數量級為109，Tm的數量級為10-2，則k=2ΔFm/Tm的數量級為1011，f0的數量級為1010，因此fb?fd，fbu和fbd都是正頻率。結合式(7)和式(8)，可以得到目標的距離信息R和徑向速度v，其表達式分別為

(9)

(10)

由上述推導發現：在單目標情況下，通過分析上下掃頻段的兩個差頻信號得到目標的距離信息和徑向速度。在多目標情況下，N個目標在上掃頻段和下掃頻段分別會產生N個差頻信號，且這2N個差頻信號由于缺少關聯信息無法正確兩兩配對，只能將其任意排列組合，得到N2個目標，其中只有N個目標是真實目標，剩下N2-N個目標都是虛假目標，虛假目標個數遠大于真實目標，目標正確識別率極低。

2 FSK-CW波形

FSK-CW信號[6]是頻率在兩個恒定頻率之間作交替變換的一種信號。單頻連續波信號可以檢測到運動目標，得到其速度信息，但是無法得到其距離信息，且無法識別靜止目標。FSK-CW信號是由兩段不同頻率的單頻信號組成的，結合兩個頻段的回波信號，還可以得到運動目標的距離信息。對于靜止目標，發射信號與接收信號的頻率是相同的，混頻低通濾波后是零頻信號，會淹沒在雜波信號中無法檢測。

雙頻調制連續波信號的時間-頻率曲線和收發信號的差頻信號如圖2所示。由圖2可得，差頻信號由四段不同頻率的恒頻段組成，其中占比較大的兩段稱為線性區域，其直接反映了運動目標的多普勒頻移。通過分析線性區域的兩個恒頻信號可以得到運動目標的距離信息和徑向速度。

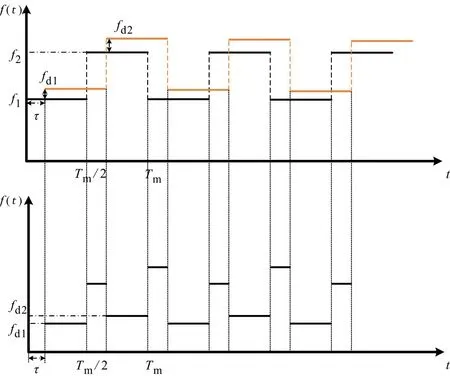
圖2 雙頻調制連續波信號的時間-頻率曲線和收發信號的差頻信號

不妨先分析前半周期頻率為恒定頻率f1的情況。設發射信號sT(t)是頻率為f1，初相為φ1的單位正弦信號。sT(t)的完整表達式為

sT(t)=sin(2πf1t+φ1)

(11)

經過延時τ，接收機接收到回波信號sR(t)，其完整表達式為

(12)

式中，fd1為對應于頻率f1產生的多普勒頻移。將發射信號與接收信號進行混頻，經過數學推導混頻信號可化簡為

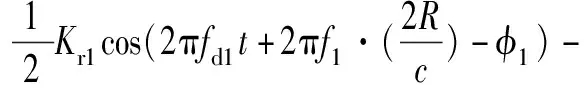
(13)

經過低通濾波濾除高頻分量，得到收發信號的差頻信號sb1(t)為

(14)

同理可得，后半周期頻率為恒定頻率f2時，收發信號的差頻信號sb2(t)為

(15)

由式(14)和式(15)可得，單頻信號所對應的差頻信號仍是單頻信號，其頻率為運動目標的多普勒頻移，其與運動目標的徑向速度一一對應，目標徑向速度v的表達式為

(16)

差頻信號的相位與目標的距離R有關，信號由于反射引起的額外相位差無法直接測得，是一個未知量，即使忽略額外相位差，由于發射信號的頻率為GHz量級的，2Rf1,2/c?1，相位已經遠遠超過2π，會產生相位模糊，無法通過單個差頻信號的相位得到距離信息。此時需要結合兩個差頻信號的相位，雖然f1,2是GHz量級的，但是其差值fstep=f2-f1是MHz量級的，將兩個信號的相位作差運算，在一定距離范圍內，可以有效解決相位模糊的問題。此外，由于信號在同一表面發生反射，其因反射引起的額外相位差幾乎相同，即φ1≈φ2，作差運算還可抵消額外相位差。目標的距離R的表達式為

(17)

式中，φb1和φb2分別為兩個差頻信號的相位，fstep為步進頻率值。

經過上述推導發現：在單目標情況下，通過分析FSK-CW信號任意一段單頻段的差頻信號，可得到運動目標的速度信息，結合兩個單頻段的差頻信號，才能得到目標的距離信息。在多目標情況下，如果多個目標的徑向速度各不相同，則各目標的差頻信號的頻率值也是不同的，在頻譜圖上容易區分。對于同一個目標，兩個差頻信號的頻率差異不大，Δfd=2(f2-f1)v/c，f2-f1為106數量級，而c為108數量級，Δfd很小，可以近似認為fd1=fd2，因此不存在同一目標的兩個差頻信號無法配對的問題。如果多個目標中有兩個或兩個以上目標徑向速度相同時，其差頻信號的頻率值相同，相位會進行疊加，無法得到各個差頻信號的真實相位，雖然仍可以通過頻率值得到目標的徑向速度，但是卻無法通過相位值得到各個目標真實的距離信息。

3 改進LFMCW波形

通過上述分析，發現在多目標情況下LFMCW波形和FSK-CW波形都存在無法正確識別目標的情況。單頻連續波得到的運動目標的速度信息可作為差頻信號的匹配依據。通過分析可得，在大多數情況下差頻信號可根據速度信息兩兩準確配對，但是當虛假目標與真實目標的速度相同時，有部分情況差頻信號的配對方式多于一種，產生配對模糊，此時需要增加額外的信息來進行篩選，否定錯誤的配對方式。FSK-CW信號還可以得到目標的距離信息，而這個距離信息剛好可以作為LFMCW差頻信號配對的額外依據。因此，在結合LFMCW信號和FSK-CW信號的基礎上，提出一種改進LFMCW信號。該信號在LFMCW前加上兩段頻率值互異的恒頻波段，兩恒頻波段組成FSK-CW信號，作為LFMCW信號上下掃頻段的差頻信號配對的依據。

改進LFMCW信號的時間-頻率曲線和收發信號的差頻信號如圖3所示。從圖3可以看出，改進LFMCW信號的差頻信號在線性區域的四段恒頻段與LFMCW信號和FSK-CW信號線性區域恒頻段一一對應。在非線性區域信號非常復雜，但由于非線性區域占比很小，可忽略不計。通過加窗技術與頻率估計算法，可以分別得到fd1，fd2，fbu和fbd的值。下面分情況討論在多目標情況下，N個fbu和N個fbd如何進行準確配對。

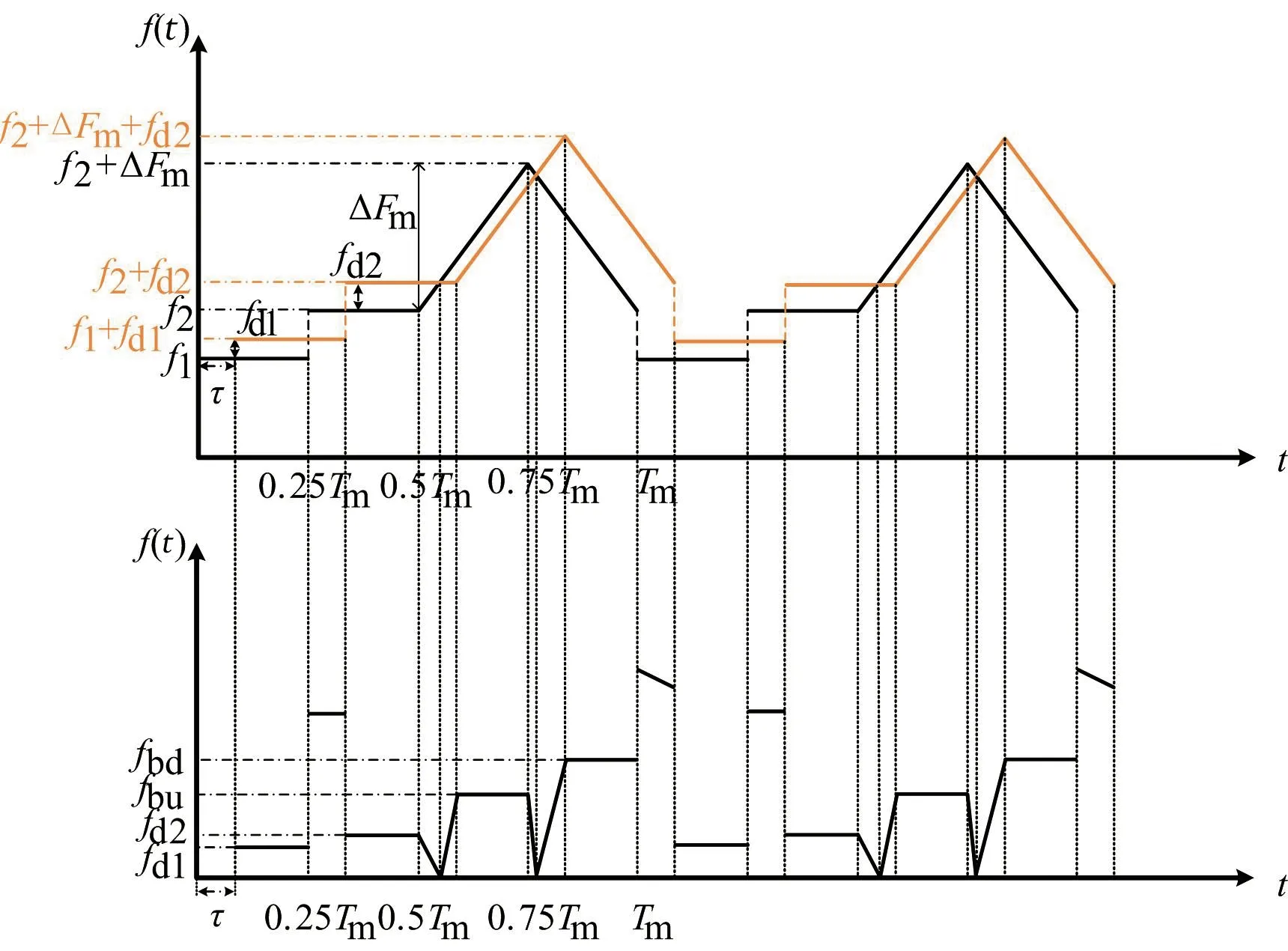
圖3 改進LFMCW信號的時間-頻率曲線和收發信號的差頻信號

根據前面分析可得，fd1和fd2近似相等，這里將fd1和fd2統一用fd表示。由式(7)和式(8)可得

|fbu-fbd|=2fd

(18)

將式(9)和式(10)聯合并進行改寫，可得

(19)

式(19)表明，v是R的一元一次函數，由fbu和fbd可以得到兩條表明v-R函數關系的直線，當fbu與fbd正確配對時，兩條直線的交點即是真實目標的(v,R)值。

為了方便討論，這里取N=3。當不存在虛假目標與真實目標速度相同時，此種情況如圖4所示。從圖中可以清晰看出，3個目標會產生9個交點，這9個可能目標的速度各不相同，此時速度信息作為匹配依據可以快速剔除虛假目標，得到真實目標。

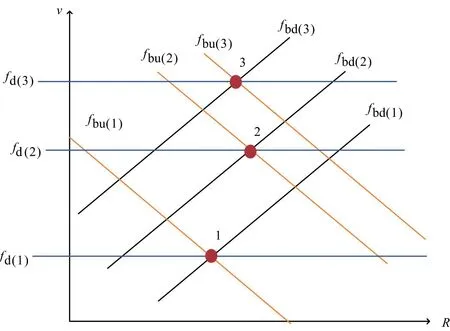
圖4 不存在虛假目標時的v-R函數關系圖

由于fbu和fbd都是擁有3條平行直線的曲線族，由幾何關系可得，與真實目標速度相同的虛假目標的個數只可能為1個、2個或4個。下面分別對以上3種情況進行分析。

當存在1個虛假目標與真實目標速度相同時，此種情況如圖5所示。從圖中可以看出，根據速度曲線篩選出了4個目標，其中在目標2和目標4中有一個為虛假目標。可以采用假設法進行配對，假設目標4為真實目標，則會產生配對沖突，說明假設不成立，目標4應為虛假目標，目標2才應該是真實目標。此時，fbu(i)和fbd(j)(i,j=1,2,3)剛好兩兩配對成功。

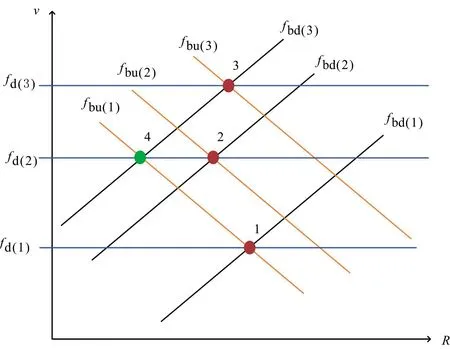
圖5 有1個虛假目標與真實目標速度相同時的v-R函數關系圖

當存在2個虛假目標與真實目標速度相同時，此種情況如圖6所示。通過分析，可以剔除虛假目標4和5，得到真實目標。

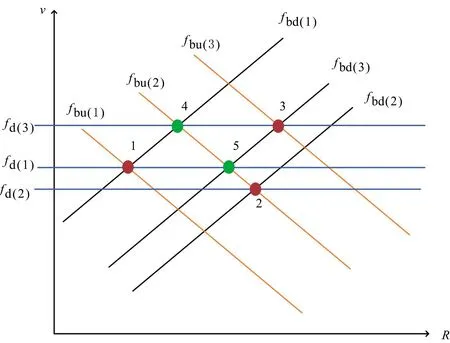
圖6 有2個虛假目標與真實目標速度相同時的v-R函數關系圖

當存在4個虛假目標與真實目標速度相同時，此種情況如圖7所示。從圖中可以看出，此時每個fd都對應不止一個目標，先嘗試采用假設法進行配對。通過配對發現此種情況下3組差頻信號對的配對方式不止一種，目標1，2，3可能為一組真實目標，目標4，5，7也可能為一組真實目標，產生配對模糊。觀察圖7，發現目標2與目標4雖然速度相同，但是其距離不同，如果可以利用距離信息進行篩選，則可以得到正確的真實目標組。改進LFMCW信號的兩段頻率值互異的恒頻波段剛好可以得到運動目標的距離信息，以此為依據可以得到真實目標。此外，當目標個數較多時，采用假設法配對過于復雜，直接利用改進LFMCW信號識別多目標效率更高。

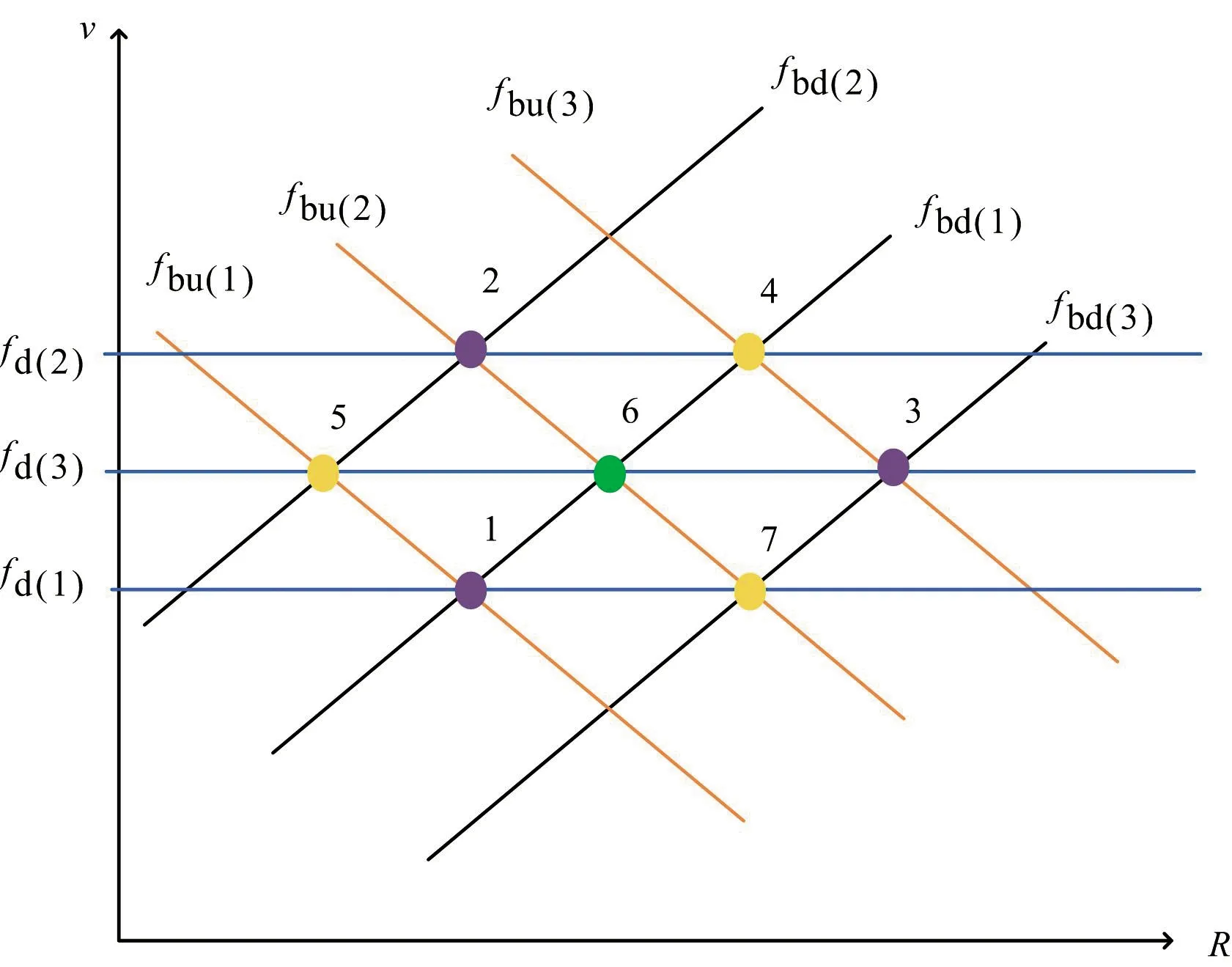
圖7 有4個虛假目標與真實目標速度相同時的v-R函數關系圖

圖8給出改進LFMCW波形識別多目標的算法流程圖。

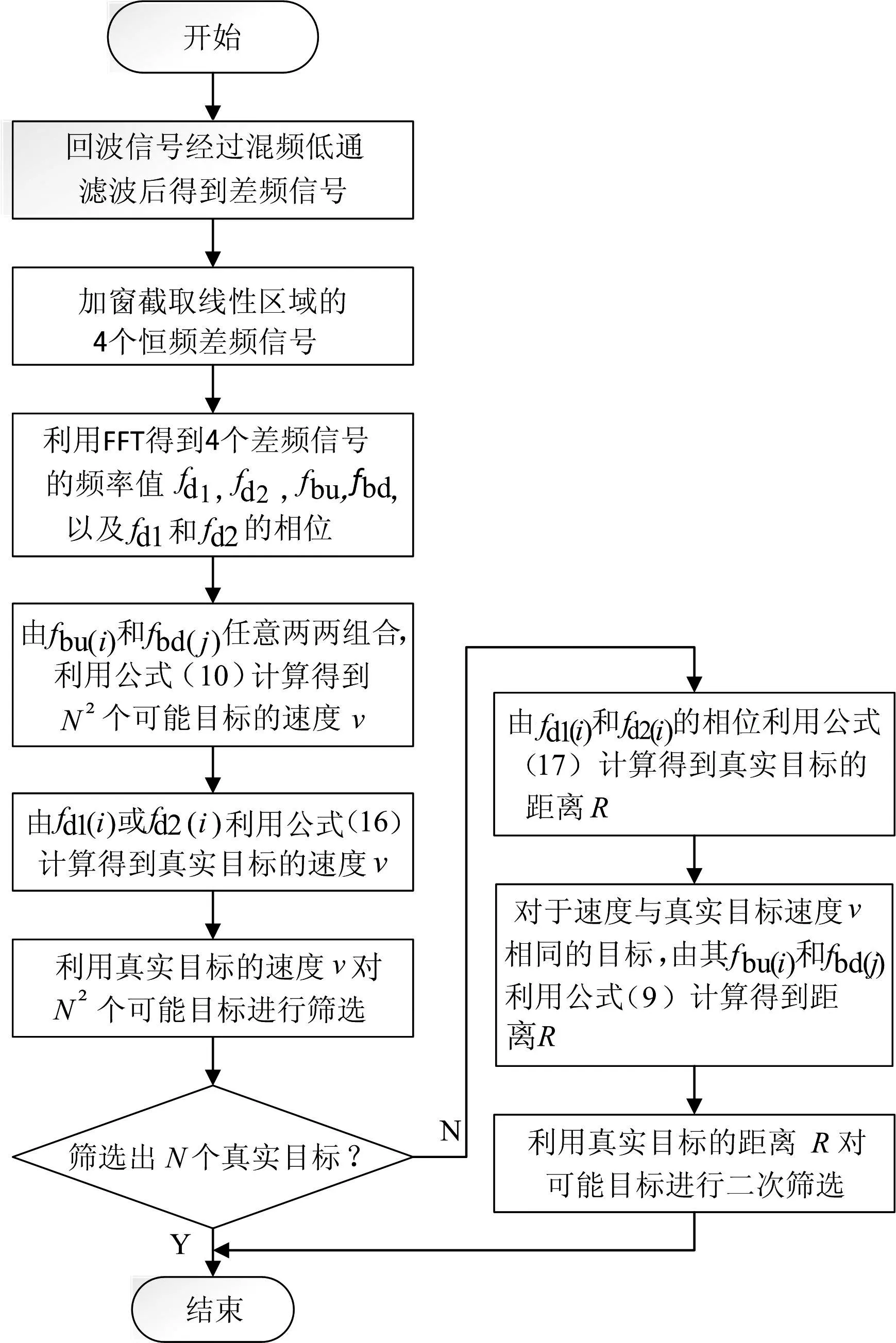
圖8 改進LFMCW波形識別多目標的算法流程圖

4 仿真實現

通過Matlab仿真實驗，驗證基于改進LFMCW波形的多目標識別算法的合理性及有效性。改進LFMCW波形的參數設置如表1所示。為了驗證算法在最壞的情況下(如圖7所示)仍然能夠準確識別多目標，通過幾何知識得到圖7所示的3個目標的(v,R)所需滿足的關系式，構建3個目標模型使其能夠滿足這些條件，3個運動目標的參數設置如表2所示。

表1 改進LFMCW雷達仿真參數設計

表2 3個運動目標的參數設置

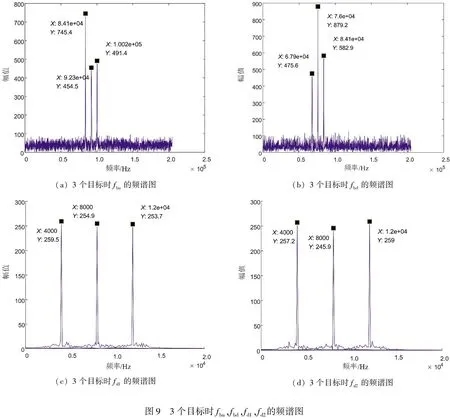
在信噪比為10 dB的條件下，當目標個數為3時，目標的回波信號經過混頻和低通濾波后得到差頻信號，加窗截取差頻信號線性區域的4個信號，分別對其作4 096點FFT變換得到對應于4個差頻頻率fbu，fbd，fd1和fd2的頻譜圖，如圖9所示。頻譜圖的橫軸為量化頻率，縱軸為頻譜幅度，頻率估計值越遠離真實頻率，幅度越小。由fbu和fbd得到目標的v-R曲線，同時由fd1和fd2得到真實目標的速度v和距離R，也將其在目標的v-R曲線上表示出來，作為剔除虛假目標的依據。

3個目標時目標的v-R曲線如圖10所示。由圖10可得，fbu和fbd的交點能夠得到9個可能目標，僅由fd1和fd2得到的速度信息無法準確識別真實目標，增加由fd1和fd2得到的距離信息作為二次篩選的依據則可以剔除所有虛假目標。由此可得，即使在最壞的情況下，改進LFMCW波形仍然能夠準確識別真實目標。由LFMCW估計得到的真實目標的(v,R)值和由FSK-CW估計得到的真實目標的(v,R)值如表3所示。由表3可得，LFMCW的距離估計誤差分別是0.063%，0.063%和0.163%，速度估計誤差分別是1.247%，1.247%和0.622%。FSK-CW的距離估計誤差分別是0.075%，0.246 %和0.284%，速度估計誤差分別是0.004 %，0.003%和0.003%。兩種算法的測距和測速精度都較高。

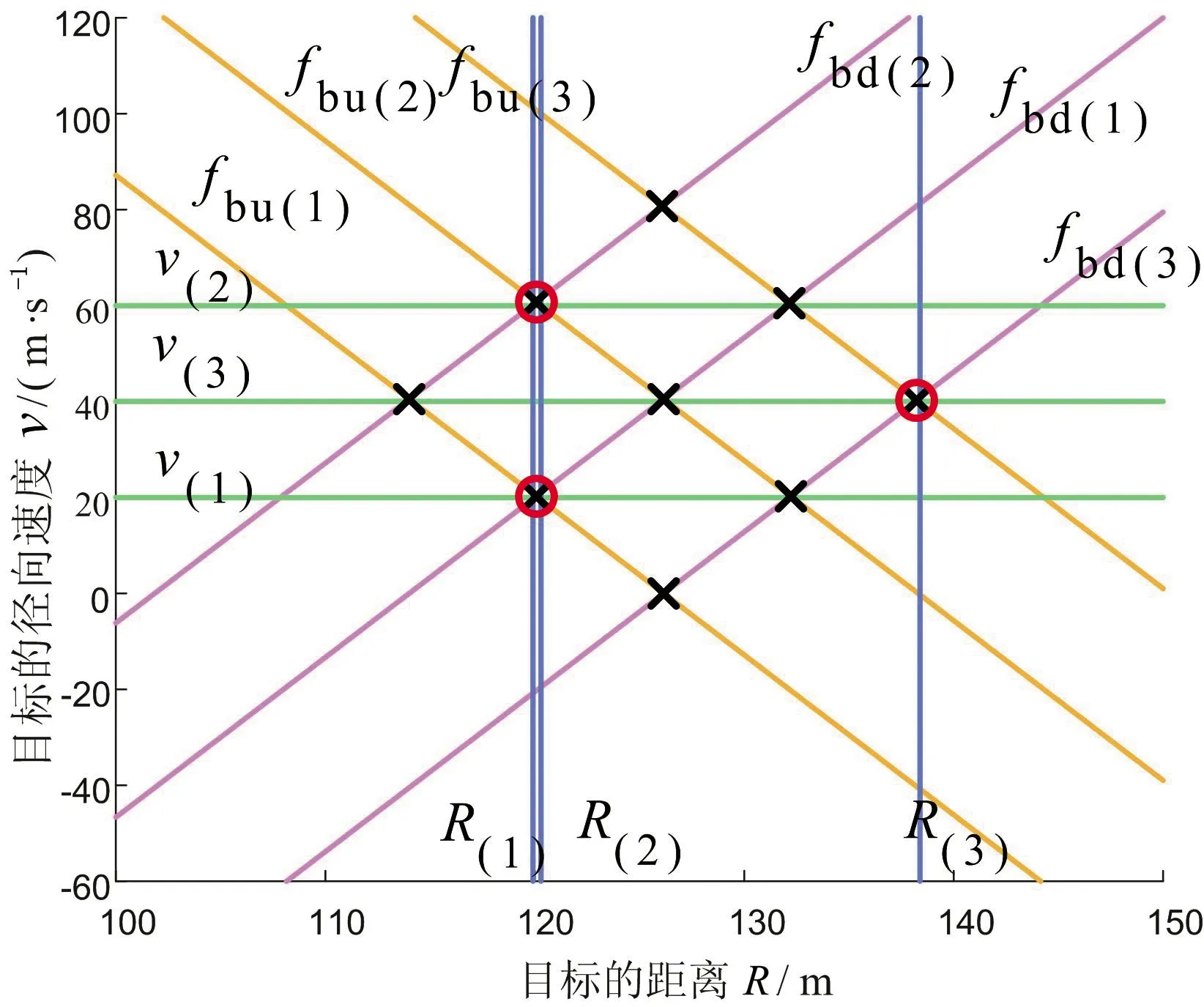
圖10 3個目標時目標的v-R曲線圖

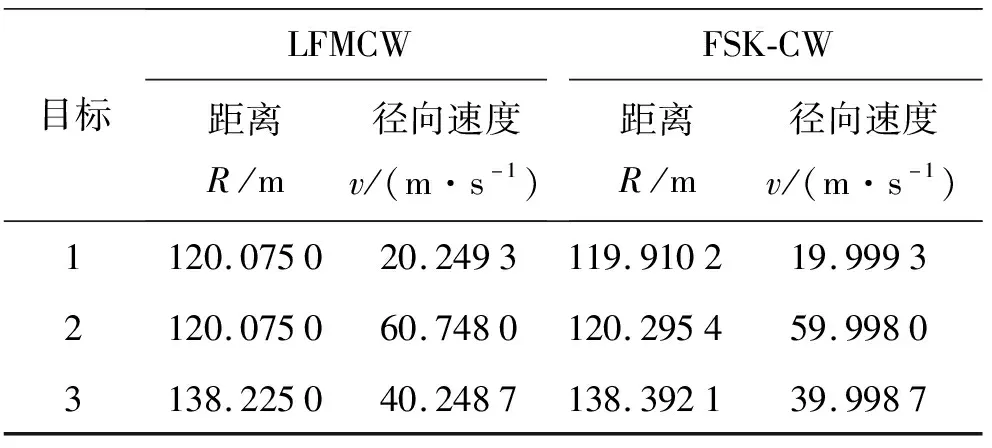
表3 由LFMCW和FSK-CW估計得到的真實目標的(v,R)值

進一步對8個目標進行仿真，8個運動目標的參數設置如表4所示。8個目標時，目標的v-R曲線如圖11所示。由圖11可得，改進LFMCW波形仍然能夠準確識別8個真實目標。

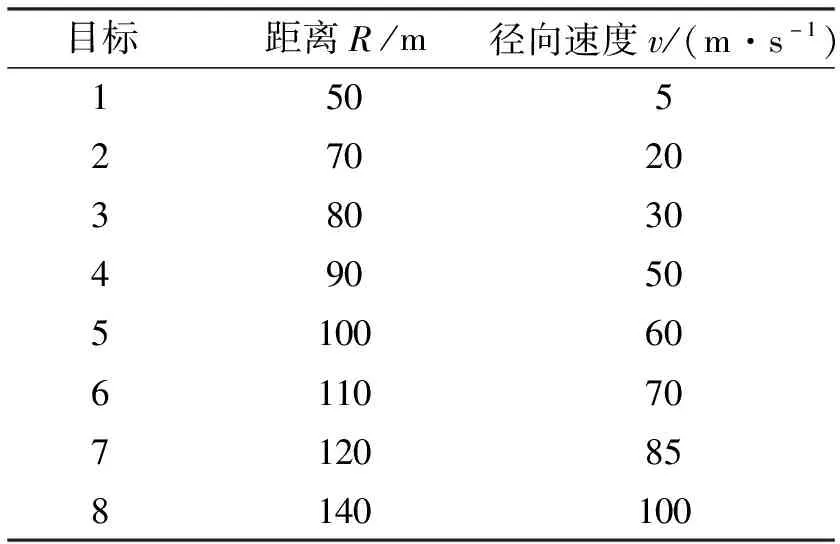
表4 8個運動目標的參數設置

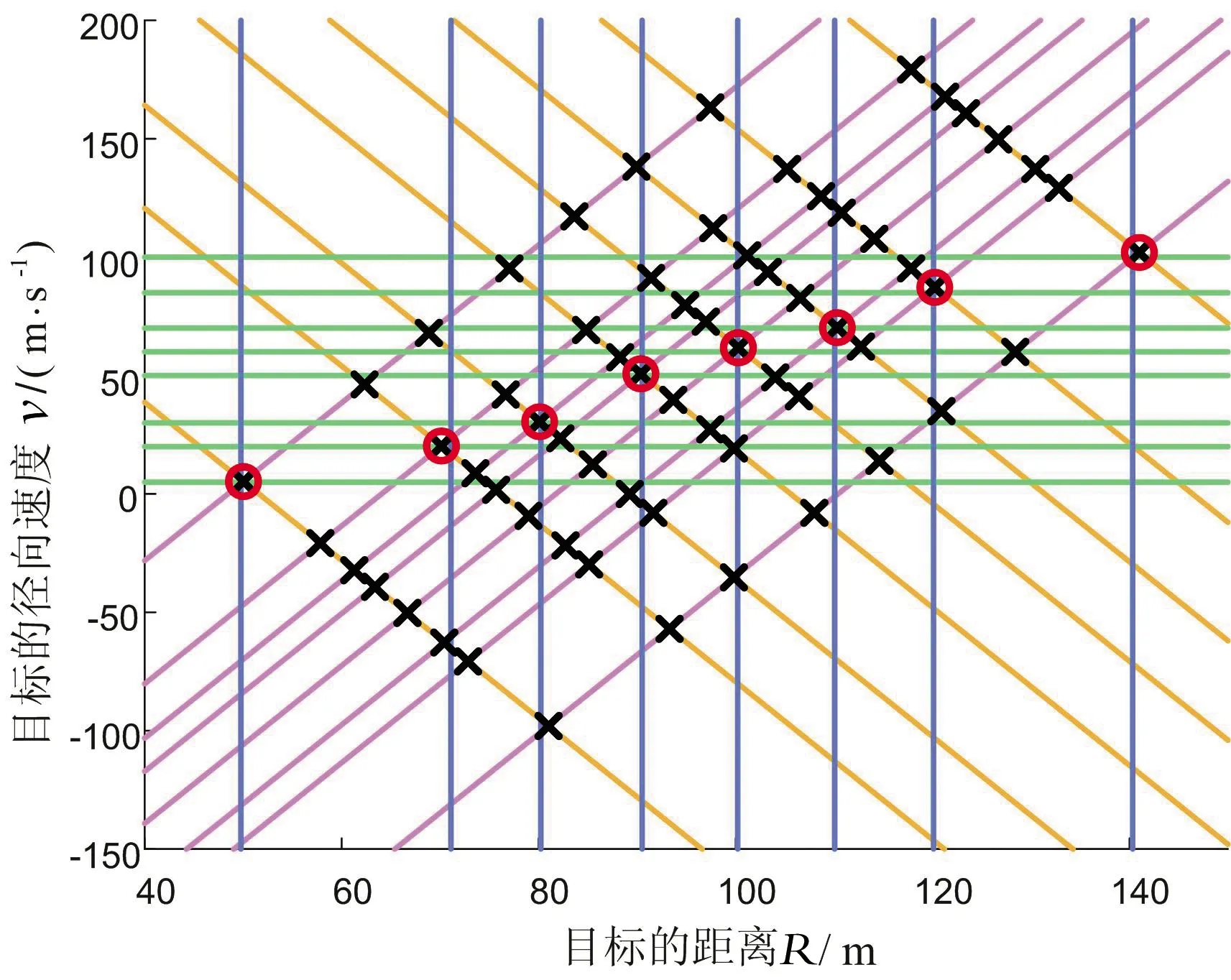
圖11 8個目標時目標的v-R曲線圖

5 結束語

LFMCW雷達在多目標情況下上下掃頻段的差頻信號由于缺乏關聯信息無法準確配對，本文針對這一缺陷，提出一種基于改進LFMCW雷達的多目標識別算法，利用FSK-CW得到的速度信息和距離信息作為LFMCW差頻信號配對的依據。仿真結果表明，改進LFMCW雷達能夠準確識別多目標，且測速和測距精度都較高。但是，基于FFT的相位估計受信噪比影響很大，當信噪比不高時，相位估計誤差較大，通過相位計算得到的距離估計值誤差也較大。可以采用更好的相位估計算法使其在低信噪比條件下也能有較高的精度。