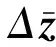基于互質陣列的外輻射源雷達低仰角估計
徐 陽,易建新,程 豐,饒云華,2,萬顯榮,熊良建
(1.武漢大學電子信息學院, 湖北武漢 430072;2.武漢大學深圳研究院,廣東深圳 518000;3.中國民航飛行學院洛陽分院,河南洛陽 471001)
0 引言
由于輻射源的低空照射限制,外輻射源雷達的目標探測主要限制在低空區域,因此如何提高外輻射源雷達的低空目標仰角估計性能一直是外輻射源雷達目標定位與跟蹤的重要研究課題,近年來眾多國內外學者對低仰角目標波達方向(Direction of Arrival,DOA)估計問題進行了大量研究[1-3]。在經典的鏡像信號模型中,目標和其鏡像被建模為兩個空間臨近的相干點源,實現對目標仰角的精確估計實際是對兩個空間臨近相干源的超分辨問題[4]。常用的超分辨技術如多重信號分類(Multiple Signal Classification,MUSIC)算法不能直接應用于相干源,若要運用MUSIC算法,需要先用空間平滑法將原陣列分為多個重疊的子陣,進行解相干預處理,這種降維處理方法是以犧牲陣列孔徑為代價的[5]。
為了彌補傳統低仰角估計問題中陣列孔徑的損失,本文考慮引入互質陣列(Coprime Array,CA)處理低仰角信號,因為互質陣列能夠在使用相同個數物理陣元的情況下,實現更大的陣列孔徑,降低了硬件的系統開銷[6]。根據質數的性質,互質陣能夠推導出一組由陣元位置差集信息構成的包含更多虛擬陣元的均勻線性陣列,從而實現陣列孔徑的擴展。相比于現有的不具有系統化陣列結構的最小冗余陣列和最小孔洞陣列等稀疏陣列[7],互質陣只需給定一對互質整數M,N就可以實現陣列的架構,陣列布設方案較為簡單直觀[8]。相比于稀疏均勻陣列,互質陣通過特有的陣列排布抑制了陣列方向圖中多個柵瓣的產生,避免了測向模糊現象,提高了角度估計的可靠性。此外,由于實現了陣列孔徑的擴展,互質陣在提高角度估計精度,分辨率和自由度方面相比于均勻線陣也具有更加優越的性能,同時還因為稀疏的陣列結構降低了天線間的互耦效應。而在低空目標波達方向估計領域,陣列的超分辨性能是一個主要的關注點,所以本文討論的是互質陣相比于相同陣元數的均勻線陣(Uniform Linear Array,ULA)在分辨率方面的優勢。
在互質陣列信號處理過程中,虛擬陣列構造方法通常用于處理非相干信號,本文討論了低仰角鏡像相干信號在虛擬陣列構造過程中的影響。文章首先在低仰角鏡像模型中,論述了利用陣元位置差集對應的協方差統計量構造虛擬陣列的原理,推導了基于相干信號的虛擬陣列接收信號形式,然后以擴展互質陣列為例詳細介紹了虛擬均勻線陣的構造過程,并通過理論分析與仿真結果展示了相干信號帶來的影響,進而闡明了虛擬陣列法在低仰角鏡像模型中的近似可行性。
1 外輻射源雷達低仰角鏡像模型
影響外輻射源雷達低仰角估計效果的主要因素是多徑效應的存在,在經典的鏡像模型里,一般暗含兩個客觀條件:1)目標與其鏡像相對于雷達的距離差很小,二者在同一個距離單元內,所以當探測低仰角目標時可認為直達路徑信號與反射路徑信號同時到達目標處并進行相干疊加。2)目標仰角為正,多徑仰角為負,二者大致相等,目標仰角小于二分之一的俯仰維波束寬度[9]。將多徑反射信號等效成與目標信號完全相干的點源,得到圖1所示的經典鏡像模型[10]。由于外輻射源雷達不主動發射信號,因此多徑建模中通常只考慮接收多徑,不考慮發射多徑。
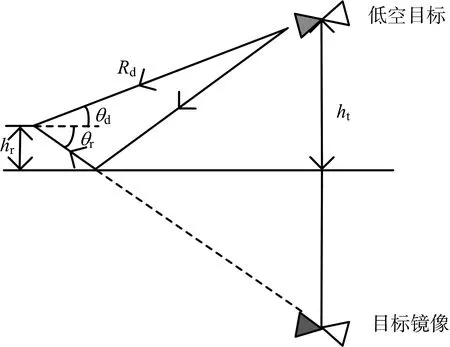
圖1 理想情況下的多徑傳播模型
設互質陣天線是由M個各項同性陣元組成的線陣,第m個陣元與陣列參考點之間的距離為dm,空中只存在一個低空目標,θd和θr分別為目標直達波與多徑信號的俯仰角。則t時刻第m個陣元接收到的數據為
xm(t)=[e-j2πdmsin(θd)/λ+εe-j2πdmsin(θr)/λ]s(t)+
nm(t)
(1)
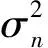
整個陣列在t時刻接收到的數據向量可表示為
x(t)=[x1(t),…,xm(t),…,xM(t)]T=
[a(θd),a(θr)][1,ε]Ts(t)+
n(t),t∈{t1,…,tL}
(2)
式中,L為快拍數,上標T表示矩陣的轉置,a(θd)=[e-j2πd1sin(θd)/λ,…,e-j2πdmsin(θd)/λ,…,e-j2πdMsin(θd)/λ]T為目標直達波方向的陣列導向矢量,a(θr)為多徑反射波方向的陣列導向矢量。
2 互質陣虛擬陣列構造
常規的互質陣列處理方法中,利用虛擬陣元位置與相關間隔一一對應的關系,將對應位置的協方差統計量作為虛擬陣列接收信號,構造虛擬均勻線陣。2.1節推導了在低仰角鏡像模型中,基于相干信號協方差統計量得到的虛擬陣列接收信號形式,2.3節則以擴展互質陣列為例,討論了相干信號在虛擬陣列構造過程中帶來的影響,闡明了互質陣虛擬陣列法在低仰角鏡像模型中的近似可行性。
2.1 基于低仰角鏡像模型的虛擬陣列構造原理
L次采樣快拍情況下,互質陣列接收信號的采樣協方差矩陣估計如下[12]:
(3)
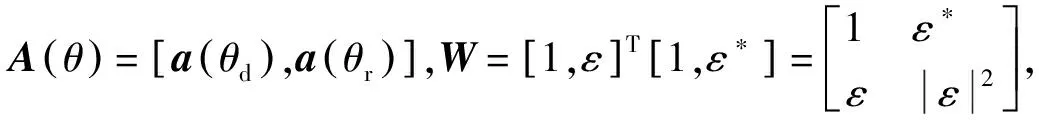
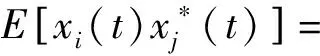
E[(e-j2πdisin(θd)/λ+εe-j2πdisin(θr)/λ)·
(ej2πdjsin(θd)/λ+ε*ej2πdjsin(θr)/λ)s2(t)]=
εε*e-j2π(di-dj)sin(θr)/λ+
ε*e-j2πdisin(θd)/λ+j2πdjsin(θr)/λ+
εe-j2πdisin(θr)/λ+j2πdjsin(θd)/λ)
(4)
根據低仰角信號模型中的暗含條件,目標仰角為正,多徑仰角為負,二者大致相等,可知θd=-θr,代入復反射系數ε=ρexp(-j4πhrsinθd/λ),上式括號中的后兩項可化為
ε*e-j2π(di+dj)sin(θd)/λ+εej2π(di+dj)sin(θd)/λ=
ρej(2hr-(di+dj))2πsinθd/λ+ρe-j(2hr-(di+dj))2πsinθd/λ=
2ρcos((2hr-(di+dj))2πsinθd/λ)
(5)
所以式(5)最終可表示為
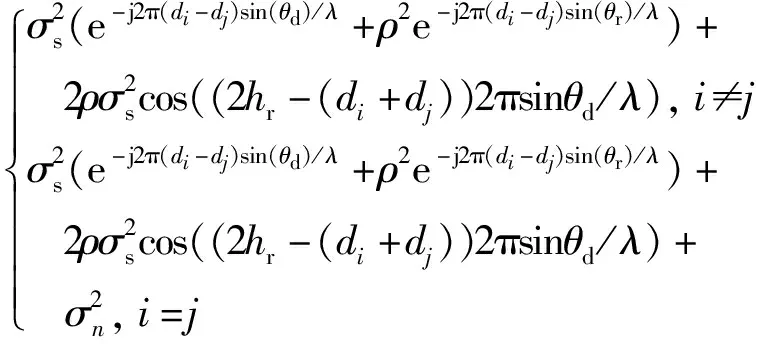
(6)
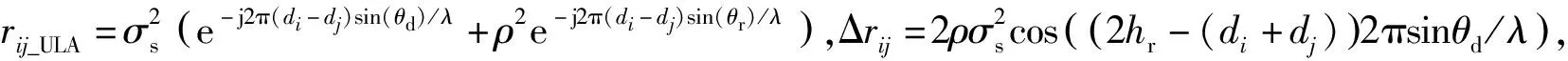
(7)
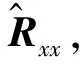
(8)
vec(·)表示矢量化操作,根據相關間隔與虛擬陣元位置的對應關系,將陣元位置差集作為虛擬均勻線陣的陣元位置坐標,從z中提取對應位置的函數值作為虛擬陣列的接收信號。2.3節將給出一個具體的構造例示,并進一步討論相干信號帶來的Δrij項的影響。
2.2 互質陣列結構
根據2.1節所述的虛擬陣列構造方法,進而可以推出空間域的陣列結構排布。
2.2.1 簡單互質陣列
簡單互質陣列的結構如圖2所示,由兩個稀疏均勻線陣構成。第一個稀疏均勻線陣包含M個陣元,陣元間距為Nd;第二個稀疏均勻線陣包含N個陣元,陣元間距為Md;M和N為互質整數,假設M小于N,d為入射到互質陣列的目標信號半波長[13]。將兩個子陣以首陣元重疊的形式進行線性疊加組合,因為M和N互質,所以除了首陣元外,其余陣元在空間中的擺放位置不會出現重疊情況,由此得到了包含物理陣元數目為M+N-1的互質陣列,最后一個陣元的位置是(N-1)Md。
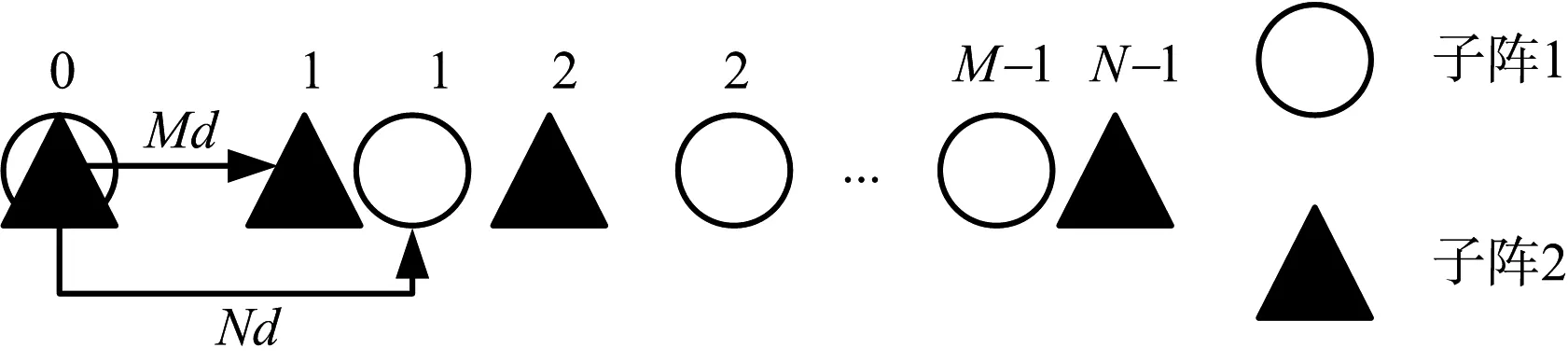
圖2 簡單互質陣列結構
將首陣元作為參考陣元,位置設為0,則兩個子陣的陣元位置差集可以表示為
{(Mn-Nm)d,0≤n≤N-1,0≤m≤M-1}
(9)
根據上式,我們用M+N-1個陣元構造了一個位于[-N(M-1),M(N-1)]范圍的差聯合陣列,但它們在這個范圍內因為存在孔洞,所以多數情況下是不連續的。例如M=3,N=4時,差聯合虛擬陣列結構如圖3所示,在-7d,7d的位置出現了孔洞。

圖3M=3,N=4虛擬陣列位置示意圖
MNd
MNd
2.2.2 擴展互質陣列
擴展互質陣列結構如圖4所示,就是將圖2中子陣1的陣元數目增加一倍,從M增加到2M個,子陣2不變,得到一個陣元數目為2M+N-1的擴展陣列。之所以這樣設定陣元數目,是利用了質數的性質。
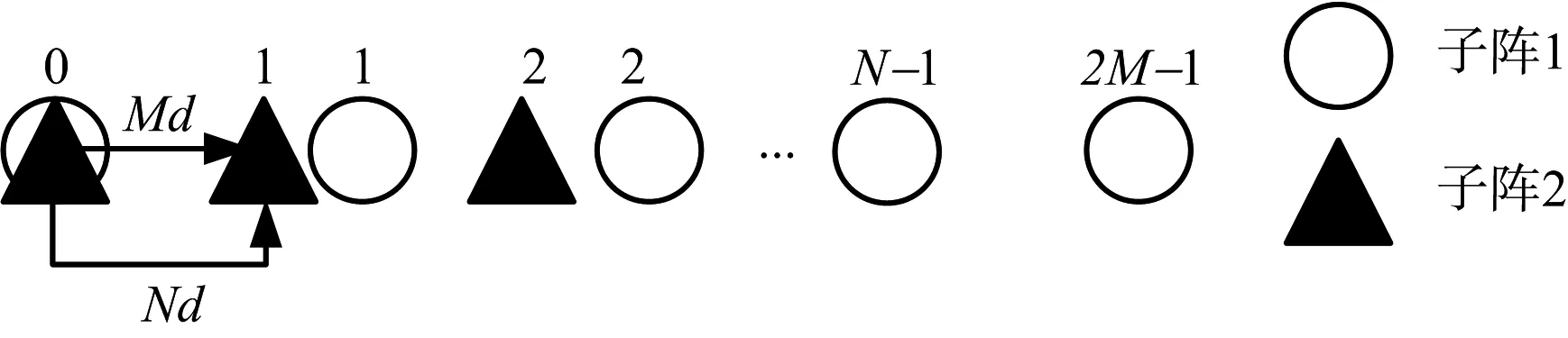
圖4 擴展互質陣列結構
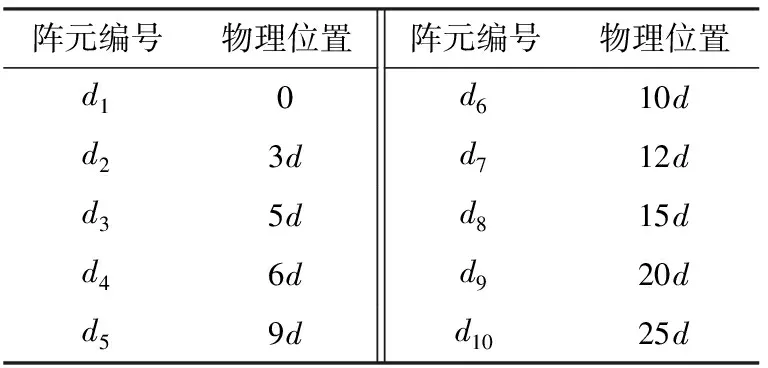
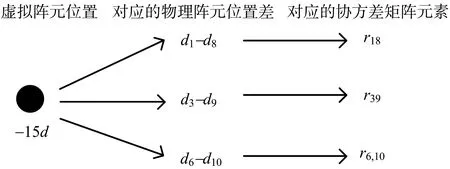
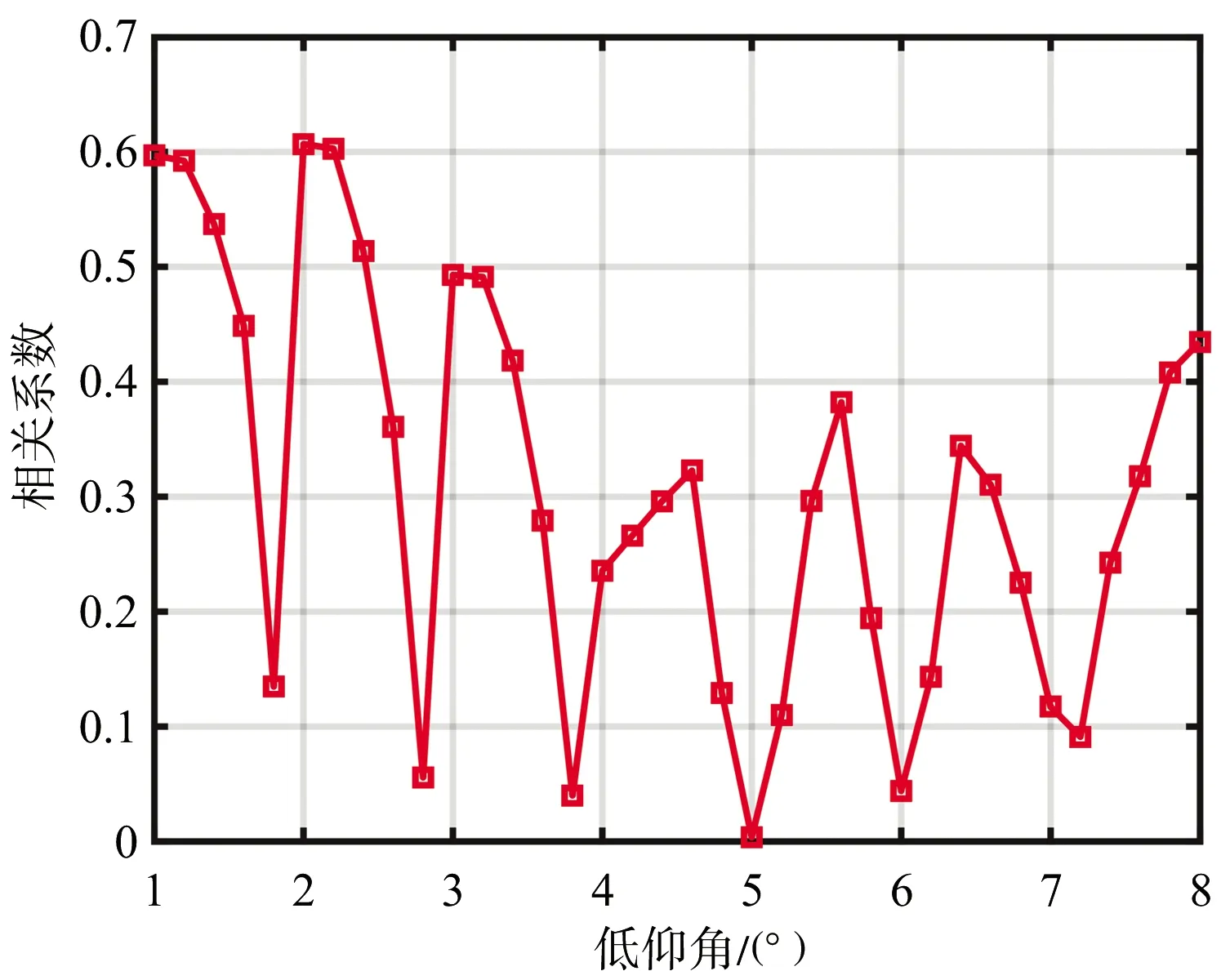
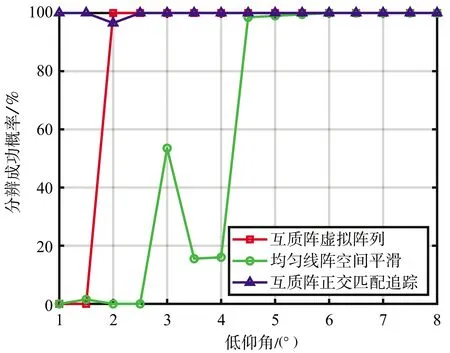
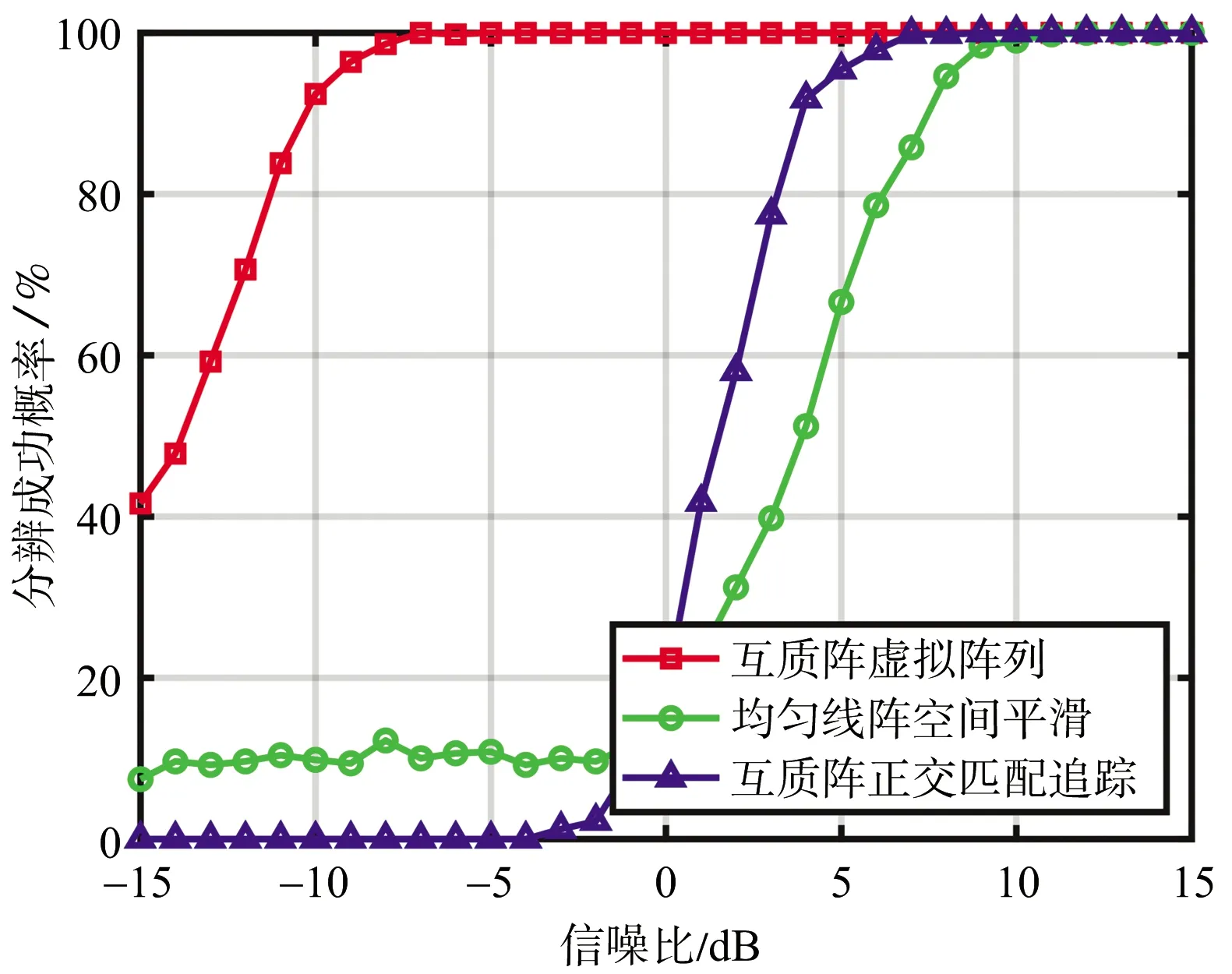
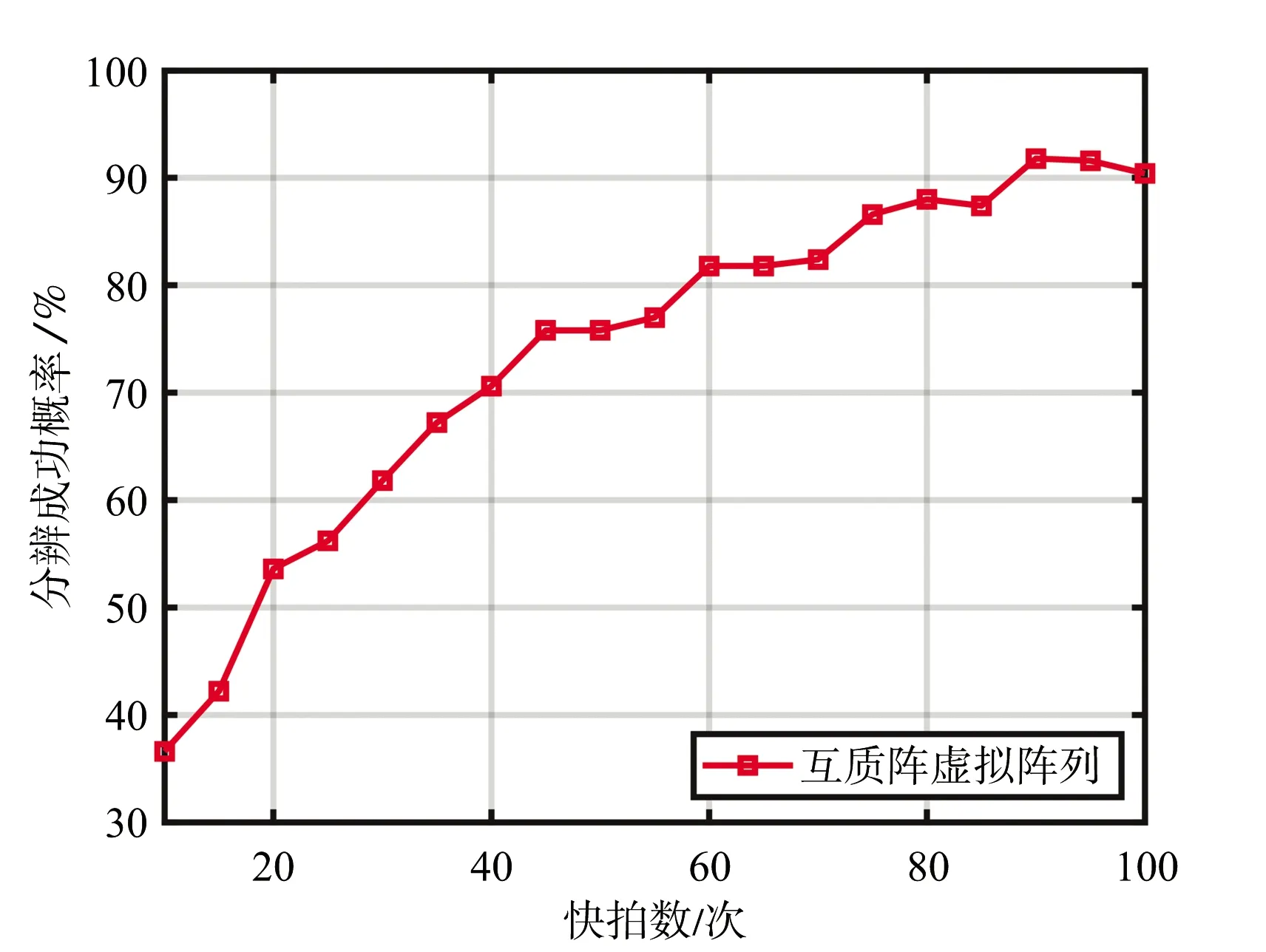
引理1[14]:假設M和N是互質整數且M 根據這個引理,m和n在上述范圍內變化時,我們可以得到-MN≤k≤MN范圍內的連續的所有整數。跟虛擬陣列的構造相結合,也就是用2M+N-1個物理陣列構造了陣元數目為2MN+1的虛擬均勻線陣,虛擬均勻線陣位置排布如下式所示: Loc2M,N={-MNd,-(MN-1)d,…, -d,0,d,…,(MN-1)d,MNd} (10) 根據2.1節的結論,我們將二階統計量作為互質陣列的等價虛擬域信號,根據相關間隔與虛擬陣元位置的對應關系,將陣元位置差集Loc2M,N作為虛擬均勻線陣的陣元位置坐標,從Rxx中提取對應位置的函數值構成列向量作為虛擬陣列的接收信號。以M=3,N=5的擴展互質陣列為例,構造一個位于[15d,15d]的虛擬均勻線陣。物理陣元的位置分布如表1所示,圖5是以-15d位置處的虛擬陣元為例,物理陣元與虛擬陣元間的對應關系示意圖,虛擬均勻線陣部分位置陣元的接收信號如表2所示。 表1 擴展互質陣陣元位置 圖5 物理陣元與虛擬陣元對應關系示意圖(以-15d位置處的虛擬陣元為例) 表2 虛擬均勻線陣部分陣元位置的接收信號 (11) 圖6 相關系數隨仰角變化 將虛擬陣列劃分成MN+1個子陣,每個子陣的陣元數目為MN+1個,第i個子陣的陣元位置為{(-i+1+n)d,n=0,1,2,…,MN},空間平滑法示意圖如圖7所示。 對MN+1個子陣對應的協方差矩陣求平均得到Rss,我們叫它空間平滑矩陣,數學上可表示為 (12) 式中,Ri表示第i個子陣列的協方差矩陣。根據文獻[16]給出的定理,描述了四階統計量和二階虛擬陣列協方差矩陣之間的關系,令Λ為對角矩陣,對角線上是入射信號功率,I是(MN+1)×(MN+1)維的單位矩陣,空間平滑矩陣可以表示成如下形式: (13) 為了展示MUSIC算法的分辨率性能,定義角度實現分辨并成功估計的條件如下: (14) 式中,θk,k=1,2為兩個信號的到達角度,θm=(θ1+θ2)/2。 2)定義當估計值與仰角真實值差的絕對值小于1°時,角度估計成功[18]。 當以上兩個條件同時成立時,我們認為角度分辨成功,定義分辨成功的概率計算如下: (15) 仿真條件:垂直放置的互質陣和均勻線陣,陣元數相同,數目為10個。互質陣是擴展互質陣列,子陣1,陣元間距為5d,陣元數目為6個;子陣2,陣元間距為3d,陣元數目為5個。均勻線陣陣元間距d,d為半波長。天線架高hr=10 m,若地勢較為平坦,低仰角情形下的鏡面反射系數ρ可假設為-1,則多徑衰減系數ε=-exp(-j40πsinθd/λ)。 基于正交匹配追蹤[19](Orthogonal Matching Pursuit,OMP)的DOA估計算法由于對信號的相干性沒有要求,常被用于相干信號DOA估計,所以仿真中用正交匹配追蹤算法跟本文闡述的虛擬陣列法(Virtual Array,VA)同時處理互質陣,并跟空間平滑法(Spatial Smoothing,SS)處理均勻線陣的結果作比較。用控制變量法比較3種方式在3個環境變量仰角、信噪比和快拍數影響下的角度分辨性能。其中OMP算法只需對正角度θd進行搜索,把仰角的搜索范圍劃分成網格θ=[θmin,θmin+Δθ,…,θmax],然后將其代入鏡像模型中的合成導向矢量asum(θd)=a(θd)+εa(-θd)構造觀測矩陣ACS=[asum(θmin),asum(θmin+Δθ),…,asum(θmax)],根據OMP算法對信號矢量進行重構得到DOA估計結果。 實驗一:在給定信噪比和快拍數的環境下,比較3種方法的角度分辨成功概率隨低仰角變化,仿真結果如圖8所示。 (a)仰角范圍以0.5°為間隔劃分 實驗參數:信噪比10 dB,快拍數100次,蒙特卡羅仿真次數500次,圖8(a)目標低仰角為1°:0.5°:8°,圖8(b)目標低仰角為1°:0.1°:8°,正交匹配追蹤算法的網格劃分為0.5°:0.5°:20°。 圖8(a)中均勻線陣前面的起伏變化是因為:仰角變化帶來衰減系數相位變化,影響空間平滑解相干效果。隨著仰角變大,直達波和多徑的間隔變大,解相干效果受衰減系數相位的影響逐漸變小,分辨概率整體呈上升趨勢,在達到1時,可以實現穩定的角度分辨。由圖8(a)可以看到,用虛擬陣列方法處理的互質陣可穩定分辨的低仰角為2°,均勻線陣的可穩定分辨低仰角為4.5°,用正交匹配追蹤法處理的互質陣可穩定分辨低仰角為1°。但由于正交匹配追蹤法的測角性能受網格劃分影響,當信號到達角與劃分網格不匹配時,角度估計性能會下降,如圖8(b)所示,如果直接對網格進行過于精細的劃分,會導致系統的運算量過大。因此可以得到結論,在給定信噪比為10 dB的環境里互質陣虛擬陣列法的角度分辨率優于均勻線陣,而正交匹配追蹤法處理的互質陣列雖然角度分辨率略優于虛擬陣列法,但估計性能受網格限制,不如互質陣虛擬陣列法穩健。 實驗二:在給定低仰角和快拍數的環境下,比較3種方法的角度分辨成功概率隨信噪比變化,仿真結果如圖9所示。 (a)仰角為5° 實驗參數:仰角分別為5°和5.5°,快拍數100次,蒙特卡羅仿真次數500次,信噪比-15:1:15 dB。 實驗三:在給定低仰角和低信噪比的環境下,互質陣虛擬陣列法的角度分辨成功概率隨快拍數變化,仿真結果如圖10所示。 圖10 互質陣角度分辨成功概率隨快拍數變化 根據圖9的仿真結果,在低信噪比環境下均勻線陣空間平滑法和互質陣正交匹配追蹤法分辨成功的概率太低,快拍數對分辨成功概率的影響沒有參考意義,所以這里只討論互質陣虛擬陣列法的角度分辨成功概率隨快拍數變化。 實驗參數:信噪比-10 dB,仰角為5°,蒙特卡羅仿真次數500次,快拍數10:5:100次。 在信噪比為-10 dB,仰角為5°的環境里,互質陣虛擬陣列法的角度分辨成功概率隨快拍數增大而增大。2.3 擴展互質陣列的虛擬均勻線陣構造

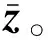

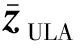
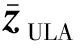
3 基于虛擬均勻線陣的空間平滑算法

4 仿真結果
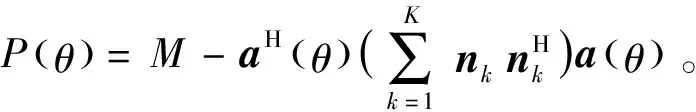
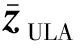
5 結束語