線性代數教學中滲透數學建模思想的探討
朱清芳 周慧倩
(洛陽師范學院數學科學學院 河南·洛陽 471934)
線性代數是大學數學的一門基礎課,內容多,比較抽象,如果按傳統的教材和教法,直接介紹定義,定理,計算,學生不清楚概念從何而來、學為何用,容易產生枯燥,難懂的想法,學習興趣和動力不足,學習效果不好。
事實上,線性代數的很多概念如多項式、行列式、線性方程組、矩陣、線性空間等都可以找到相應的實際問題,作為概念的實例引入,反過來又可以用代數概念和方法來解決實際問題.這樣,不但能提高學生的學習興趣,使他們更好的理解代數概念,而且能體驗到探索、發現和創造的過程.在實際教學過程中,無論是在數學概念的講解中,還是在對問題的分析以及思維的拓展上,不斷的、反復的強調數學建模的思想,將數學建模思想融入到每一個教學細節上,不論是對我們學生掌握好數學知識,還是培養創新思維能力,都是很好的實踐手段.下面從概念引入和理論應用兩個方面舉例加以說明。
1 概念的引入
很多線性代數概念都具有明顯的幾何或者實際生活背景,如果從背景出發,通過實際問題建立數學模型來引入代數概念,將很大程度上減輕概念的抽象性,使學生更好的理解概念,激發學習興趣。
行列式,矩陣,線性方程組,特征值,線性空間等概念都可以這樣引入。
實例1:矩陣概念的引入。
問題1:某航空公司在A,B,C,D四城市之間開辟了若干航線,如圖所示表示了四城市間的航班圖,如果從A到B有航班,則用帶箭頭的線連接A與B,若兩城市之間沒有航班則不用連線:

則右圖可以用矩陣表示為
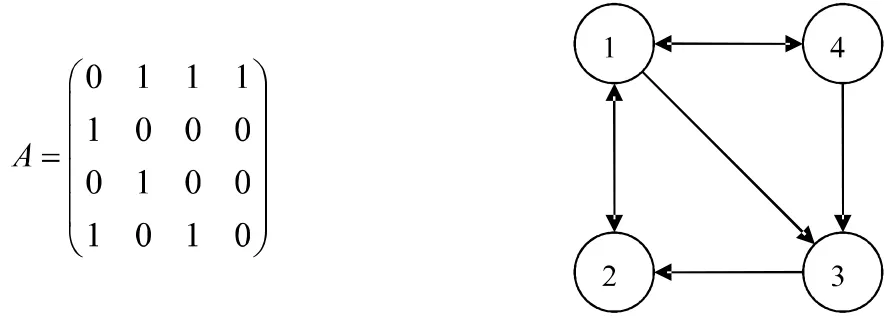
而在實際生活當中,可能會有更多的城市。通過上述矩陣,就可以高效的輸入這樣一個航班關系圖,并且使得計算機能夠識別并且快速有效處理這樣的圖形。
在上面的這樣一個實例中,實際上已經應用了如下數學建模手段:圖的概念引入;將圖轉化為矩陣的思想。
問題2:討論一個兩人零和對策問題.兩兒童A,B玩游戲,每人只能在{石頭,剪刀,布}中選擇一種,當A,B各選擇一種策略時,就確定了一個“局勢”,也就定出了各自的輸贏,規定勝者得1分,負者失1分,平手各得零分,則A的得益可用下述矩陣表示:

實例2:矩陣特征值和特征向量概念的引入。
問題:一種昆蟲,第一組為幼蟲(不產卵),第二組每個成蟲在兩周內平均產卵100個,第三組每個成蟲在兩周內平均產卵150個。假設每個卵的成活率為0.09,第一組和第二組的昆蟲能順利進入下一個成蟲組的存活率分別為0.1和0.2.假設現有三個組的昆蟲各100只,計算第2周、第4周、第6周后各個周齡的昆蟲數目,并考慮下面問題:
(1)以兩周為一時間段,分析這種昆蟲各周齡組數目演變趨勢.在兩個相鄰的時間段,各周齡組的昆蟲數目變化的比例是否有一個穩定值?昆蟲數目是無限增長還是趨于滅亡?原因是什么?
(2)如果使用一種除蟲劑可以控制昆蟲的數目,使得各組昆蟲的成活率減半,問這種除蟲劑是否有效?
對上述昆蟲繁殖問題建模解答中,主要使用的是萊斯利矩陣模型以及萊斯利矩陣的特征值。
2 理論的應用和思維的拓展
實例3:動物數量的按年齡段預測問題。
問題:某農場飼養的某種動物所能達到的最大年齡為15歲,將其分成三個年齡組:第一組,0~5歲;第二組,6~10歲;第三組,11~15歲.動物從第二年齡組起開始繁殖后代,經過長期統計,第二組和第三組的繁殖率分別為4和3.第一年齡和第二年齡組的動物能順利進入下一個年齡組的存活率分別為12和14。假設農場現有三個年齡段的動物各100頭,問15年后農場三個年齡段的動物各有多少頭?
問題分析與建模:因年齡分組為5歲一段,故將時間周期也取為5年,15年后就經過了3個時間周期。設表示第k個時間周期的第 i組年齡階段動物的數量(k=1,2,3;i=1,2,3)。
因為某一時間周期第二年齡組和第三年齡組動物的數量是由上一時間周期上一年齡組存活下來動物的數量,所以有
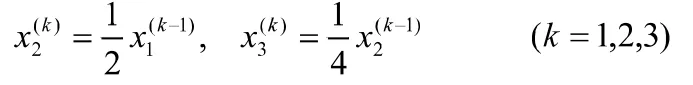
又因為某一時間周期,第一年齡組動物的數量是由于一時間周期各年齡組出生的動物的數量,所以有

結果分析:15年后,農場飼養的動物總數將達到16625頭,其中0~5歲的有14375頭,占86.47%,6~10歲的有1375頭,占8.27%,11~15歲的有875頭,占5.226%.15年間,動物總增長16625-3000=13625頭,總增長率為13625/3000=454.16%。
這樣一個問題是為了引入矩陣的相似對角化計算矩陣的方冪而提出,而實際生活當中還有許多類似的問題,比如人口的遷移問題、就業人員的流動問題等等。
實例4:行星軌道計算問題。
問題:一天文學家要確定一顆小行星繞太陽運行的軌道,他在軌道平面內建立以太陽為原點的直角坐標系,在兩坐標軸上取天文測量單位(一天文單位為地球到太陽的平均距離:1.4959787×1011m).在5個不同的時間對小行星作了5次觀察,測得軌道上5個點的坐標數據如下表:
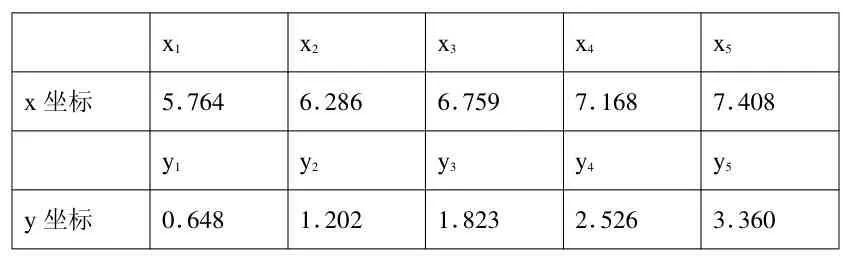
?
由開普勒第一定律知,小行星軌道為一橢圓.請建立小行星軌道的方程:
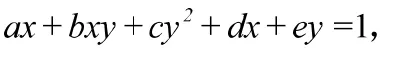
并確定橢圓的焦點坐標,長軸,短軸的長度。
對如上實例的求解實際上是解一個線性方程組,但我們在課堂上提出了這樣的問題,就實際意義而言,觀測數據總是有誤差的,因此,觀測的數據越多對我們計算越有利,但是若有更多的數據,則得到的方程組可能無解.然后由此引入線性回歸最小二乘數學模型:在實際生活當中有些問題沒有理論上的數學解,但是應用已有的數學知識,我們仍然可以通過數學方法得到需要的解。另一方面,計算橢圓的焦點坐標,長軸,短軸的長度乃是線性代數的二次型理論在解析幾何進而在實際問題中的一個典型應用.通過這樣一個實例讓學生體會到數學建模的無處不在,高等代數在數學模型求解當中的一個又一個的應用。
數學建模方法能夠使數學知識形象化、系統化和實用化,同時數學建模思想是學習數學的催化劑和認識理論規律的有力武器.在高等代數的一些概念、定理的教學中滲透數學建模思想,有助于分清各知識脈絡以及它們的聯系,數學建模思想能將知識向深度和廣度延伸,高等代數中有許多具體問題和定理還值得深入挖掘其中的知識點;與其它學科相結合方面的問題也有待進一步探討。

