大埋深對明挖地鐵車站出入口結構影響分析
汪子豪 歐陽院平 洪亮
摘 要:以武漢地鐵 12 號線某明挖車站的出入口結構為背景,計算分析出入口結構頂板底埋深 5m、9m 和 18m 3 種條件下不同結構截面時的結構受力,分析大埋深對出入口結構的影響。結果表明,與一般埋深下的出入口結構不同,當結構埋深較大時,結構自重對受力影響相對較小,增加截面尺寸能夠顯著降低結構受力;在作對比分析時,引入正則彎矩概念,對不同埋深時結構正則彎矩與結構截面的關系進行計算分析,進而對大埋深出入口結構截面進行優化。
關鍵詞:地鐵;明挖車站;大埋深;出入口結構;正則彎矩;優化分析
中圖分類號:U231.3
地鐵明挖地下車站出入口附屬結構作為聯系外部空間和車站內部空間的主要通道,其安全性十分重要,結構設計還應兼顧其經濟性。出入口通常在地下一層與主體結構相連接,其基坑開挖深度一般在10 m左右,工程計算中,往往可以采用較為固定的斷面設計尺寸[1-4]。然而隨著地鐵建設規模逐步擴張,線網規劃趨于復雜,附屬結構的設計受限于建筑紅線、控制管線、交通組織、線路換乘等因素[5-8],大埋深出入口的非典型情況越來越多見[9-10]。
本文結合武漢地鐵12號線某出入口結構實例,研究地下車站出入口結構不同埋深時的結構受力,對大埋深出入口結構截面進行優化。
1 結構設計模型
武漢地鐵12號線某明挖車站受限于市政管線改遷和線路交叉等因素,出入口基坑開挖深度最大達20余米。本文采用有限元模擬頂板底埋深5 m~18 m的出入口標準斷面。
1.1 基本假定
明挖車站的出入口結構標準斷面為箱形鋼混結構,結構縱向荷載分布無突變,底板地基承載力均勻,其結構受力分析可簡化為平面問題[11-14]。地鐵車站結構一般采用彈性分析方法,驗算承載力大小和裂縫寬度。計算模型中,底板下設置豎向受壓土彈簧支撐;考慮結構最不利受力情況進行荷載組合,迎土面按照0.2mm裂縫控制配筋,背土面和車站內其他部位按照0.3mm裂縫控制配筋[15-17];結構設計按使用年限100年考慮,不考慮抗震工況和偶然組合。
1.2 計算模型
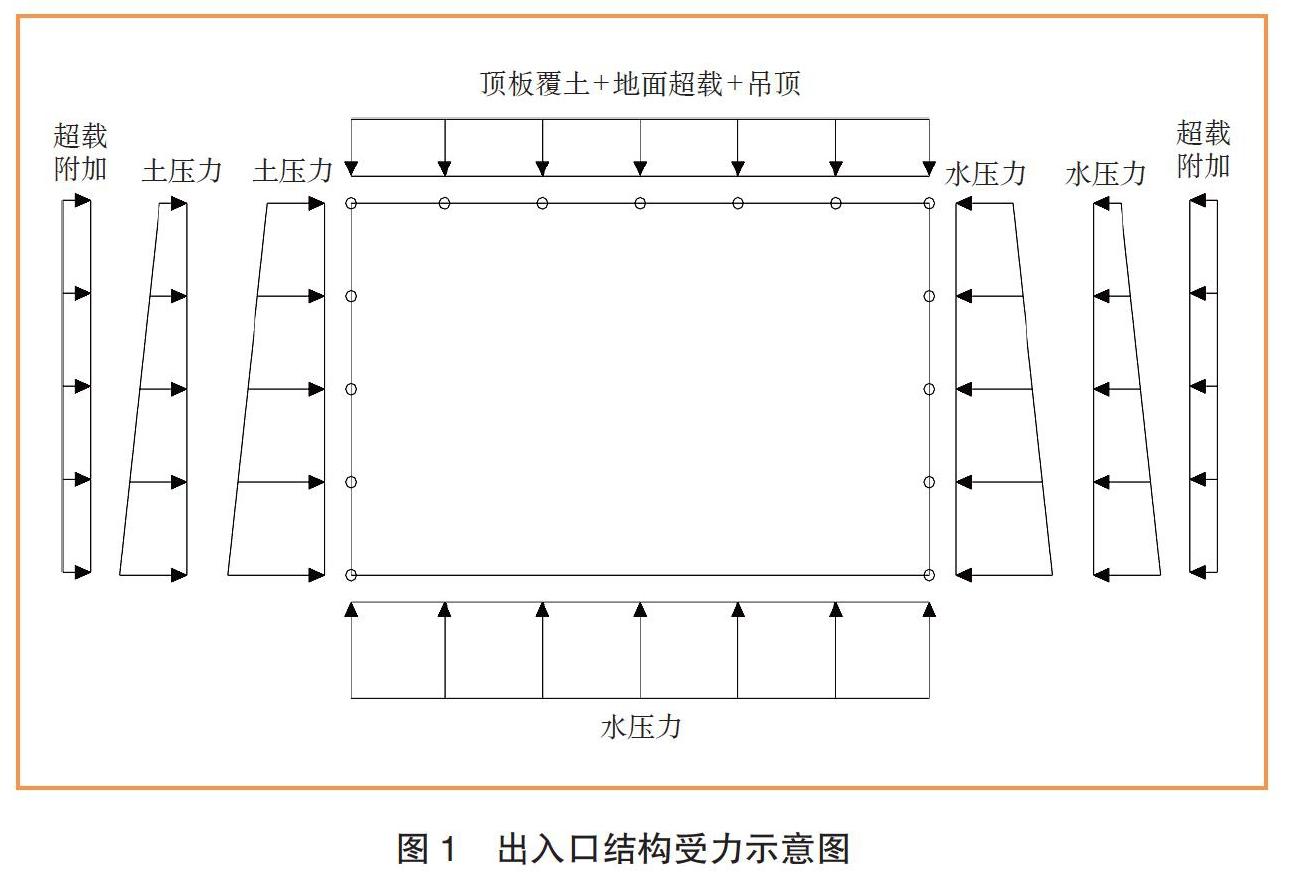
出入口結構標準斷面的結構凈高4.2 m,凈寬6.5m,采用C35抗滲混凝土。計算中,分別對頂板底埋深5m、9 m和18 m3種條件下的出入口結構標準斷面進行分析;考慮土壓力、水壓力、頂板覆土和地面超載4 類荷載作用,偏安全考慮取地表為抗浮水位[18-20],其受力示意圖如圖1所示。當頂板底埋深為5 m時,出入口底板所受水浮力約為100 kN;當頂板底埋深達到18m時,出入口底板所受水浮力增加約230 kN,相應地,頂板覆土壓力也由約40 kN增加至約170 kN。
2 結構模擬分析
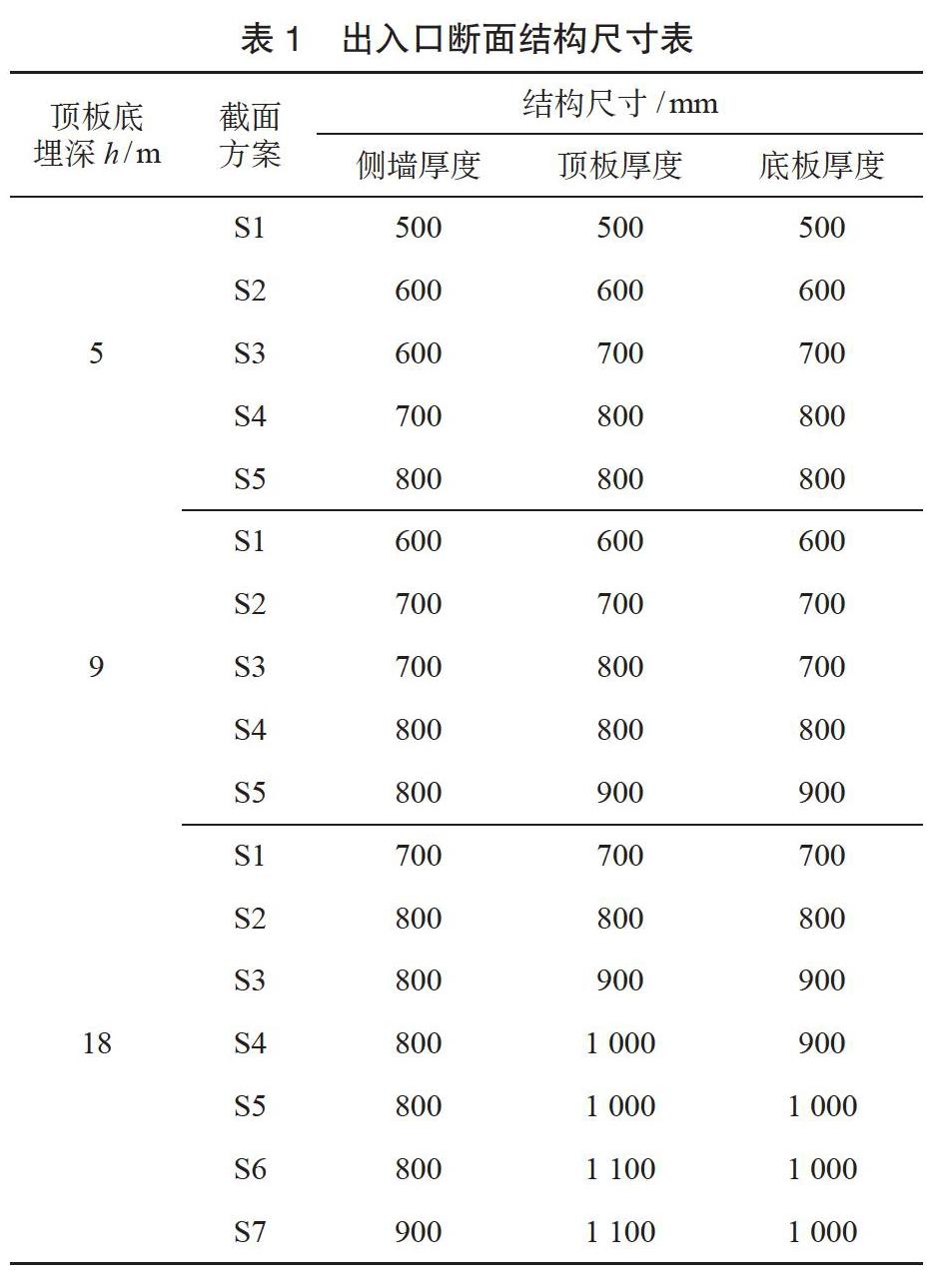
本節將對頂板底埋深分別為5 m、9 m和18 m的標準出入口結構進行比較分析,出入口結構斷面均為標準斷面。結合結構受力和實際情況,對每一種頂板底埋深的情況取5~7組結構尺寸組合,如表1所示。
分別計算不同結構厚度下的結構內力,綜合比選承載力和裂縫分析結果,得到不同埋深條件下的最優結構尺寸。當荷載條件相同時,隨著結構尺寸變化,結構內力也會發生變化;結構厚度越大的截面,其承載能力越強。為便于對比,本節將采用板厚對彎矩進行正則化。
2.1 頂板底埋深 h = 5 m 出入口結構分析
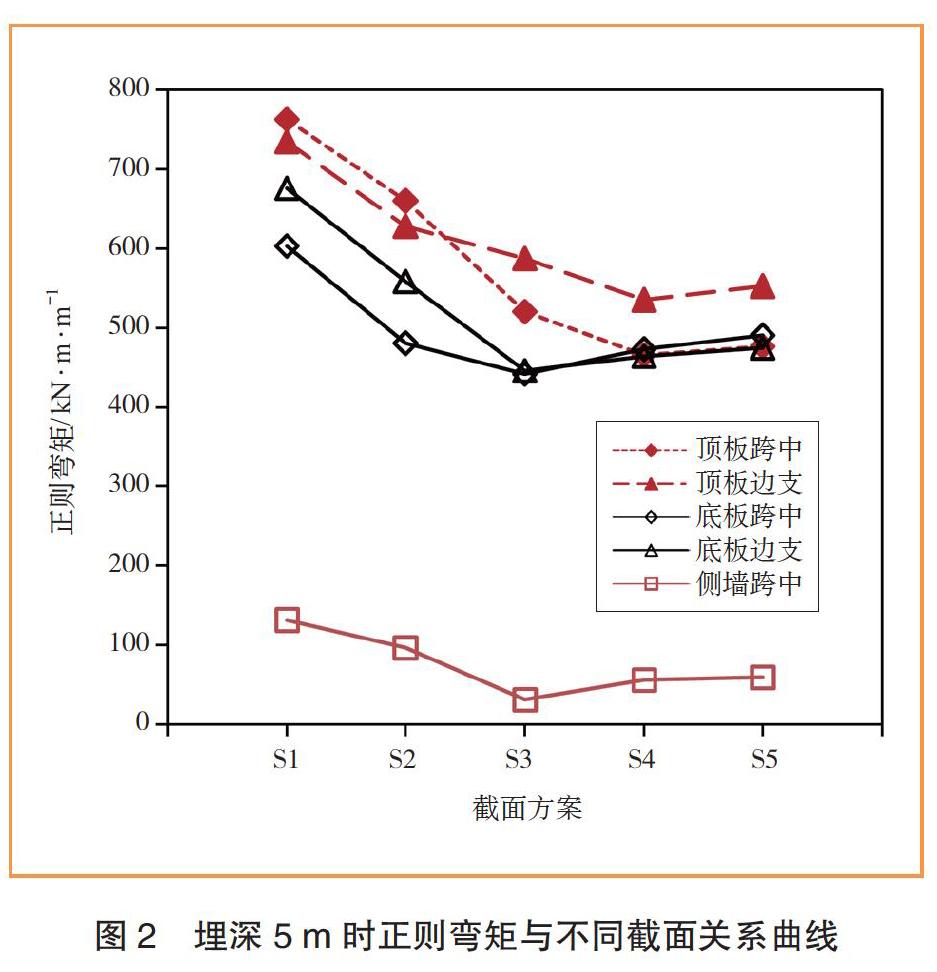
出入口結構頂板底埋深h = 5 m時,不同標準斷面尺寸下的準永久彎矩如圖2所示,圖2中橫坐標對應表1中的不同截面方案,縱坐標的正則彎矩為結構彎矩與對應位置截面厚度的比值。
由圖2可知,隨著截面厚度的增加,不同截面位置的正則彎矩均呈現出減小趨勢;側墻跨中正則彎矩值相對較小,不是計算結構尺寸的決定性因素;當截面增大到截面方案S3時,底板跨中和邊支的正則彎矩均達到最小值;截面方案從S3增加到S4時,頂板、底板及側墻的厚度均增加100 mm,此時頂板的正則彎矩減小,底板和側墻跨中則不降反升。由此可見,截面方案S3至S4的截面尺寸增大帶來的承載能力提升不顯著,不足以抵消底板和側墻的彎矩增加;此后隨著截面增大,正則彎矩幾乎不變。
綜合考慮結構安全性和經濟性,計算頂板底埋深h = 5 m時截面方案S1至S5的承載力和裂縫,此出入口標準截面的最佳截面方案為S3。
2.2 頂板底埋深 h = 9 m 出入口結構分析
出入口結構頂板底埋深h = 9 m時,不同標準斷面尺寸下的正則彎矩如圖3所示。類似地,隨著截面厚度的增加,不同截面位置的正則彎矩均成減小趨勢,側墻跨中彎矩值相對較小;截面方案從S2增加到S3時,僅頂板厚度增加100 mm,此時頂板和側墻跨中正則彎矩減小,底板則在邊支位置正則彎矩減小,在跨中位置相應增加;對于截面方案S3至S5,結構正則彎矩變化幅度較小,即此時截面尺寸增加對結構承載能力的提升效果不顯著。
綜合考慮結構安全性和經濟性,計算頂板底埋深h = 9 m時截面方案S1至S5的承載力和裂縫,此出入口標準截面的最佳截面方案為S3。
2.3 頂板底埋深 h = 18 m 出入口結構分析
出入口結構頂板底埋深h = 18 m時,不同標準斷面尺寸下的正則彎矩如圖4所示。隨著截面厚度的增加,不同截面位置正則彎矩基本保持減小趨勢,側墻跨中正則彎矩值相對較小;截面方案從S2增大到S3時,頂板和底板厚度均增加100 mm,正則彎矩均有明顯明顯減小;截面方案從S3增大到S4時,僅頂板厚度增加100 mm,此時頂板和側墻跨中正則彎矩均減小,底板則幾乎不變,僅其邊支位置正則彎矩略有增加,頂板和底板正則彎矩仍較大,對結構承載力和裂縫進行計算可知,此時結構配筋率仍較高;當出入口結構截面繼續增大,即截面方案從S4增大到S5時,僅底板厚度增加100 mm,此時底板正則彎矩顯著減小,頂板則變化較小;當截面從S6增大至S7時,僅側墻厚度增加100 mm,頂板和底板跨中彎矩均略為減小,且各邊支處正則彎矩不降反升。由此可見,為優化出入口結構截面尺寸和配筋率,增加底板厚度的效果與增加頂板厚度相一致。

