重力式碼頭卸荷板工作機制有限元分析

扈世龍，張建球

(廣西交科集團有限公司，廣西 南寧 530007)

卸荷板是重力式碼頭常見的組合構件，在我國最早于1958年應用于方塊碼頭[1]，目前已廣泛應用于沉箱和坐床式圓筒碼頭。卸荷板的作用效果主要體現在其卸荷效應能減少墻背側向土壓力、懸臂段自重和上方填料自重增加能使結構體重心整體后移及平衡地基應力，從而使結構體整體的穩定性和適應性得到增強。

國內外針對卸荷板的研究主要是關于墻背側向土壓力卸荷效應和土壓力計算方法等的探討。卸荷效應模型試驗研究[2]表明，設置卸荷板后墻背側向土壓力減少，卸荷效果可達到12%～30%，有研究認為從平衡關系出發卸荷的根據不足[3]；合理位置與長度模型試驗[4]表明卸荷板懸臂越長，卸荷效果越好，卸荷板位置降低可進一步減小墻背主動土壓力，也有人通過理論和有限元分析[5-7]認為隨著位置和長度的變化，卸荷效果表現為先增大后減小的特征，卸荷板的最佳位置在0.3～0.6倍墻高。計算方法研究[8-10]表明，上墻墻背土壓力計算可采用第二破裂面法、朗肯土壓力法等，下墻墻背土壓力計算可采用直線卸荷法、矩形分布法、力的多邊形法等。總之，根據前人的研究結果，首先都認為設置卸荷板對增強結構整體穩定具有顯著效果，但是對卸荷板卸荷效果和墻背土壓力的計算方法還存在爭議；其次，研究人員更多關注卸荷板遮簾效果減小下墻墻背土壓力的特點，而對卸荷板上墻墻背土壓力、懸臂段自重和上方填料自重變化對結構整體穩定的影響特點關注較少。此外，還有部分研究[11-12]注意到結構體墻背土壓力的分布與結構體整體變形存在聯系。

本文通過建立有限元概化模型，探討重力式方塊碼頭懸臂卸荷板的工作機制，一是對比分析卸荷板的卸荷效果和其上方填料自重、懸臂段自重分別對增強碼頭整體穩定的貢獻率；二是分析結構體墻背土壓力分布與結構體整體變形的關系，探究墻后土體整體分布特點。并以此為基礎討論卸荷板懸臂長度和位置的影響特點。

1 有限元模型

采用通用有限元軟件ANSYS進行計算，假定重力式空心方塊碼頭橫向截面均相同，建立二維平面概化模型。

模型結構體采用帶卸荷板重力式空心方塊結構，上部胸墻頂寬1.2 m，墻高3.0 m，中部懸臂式卸荷板厚1.0 m，懸臂長度2.5 m，下部空心塊體高4.0 m，寬3.0 m，側壁厚和底厚0.4 m，前趾長0.7 m，空心方塊腔內回填塊石；墻后回填土體簡化為細砂層；結構下部基床簡化為厚3 m塊石層；基床下部簡化為頁巖層；頂面均布堆載強度為30 kPa，均布堆載范圍從距碼頭前沿1.2 m位置(緊接胸墻)起始。模型X向和Y向均采用8倍擋墻高度的計算范圍，即模型的計算范圍為64 m×64 m，左、右側邊界Uy可自由移動，Ux約束，下部邊界Uy和Ux全約束，墻底與基床的摩擦系數為0.45。材料參數選擇見表1，建立的概化模型見圖1。

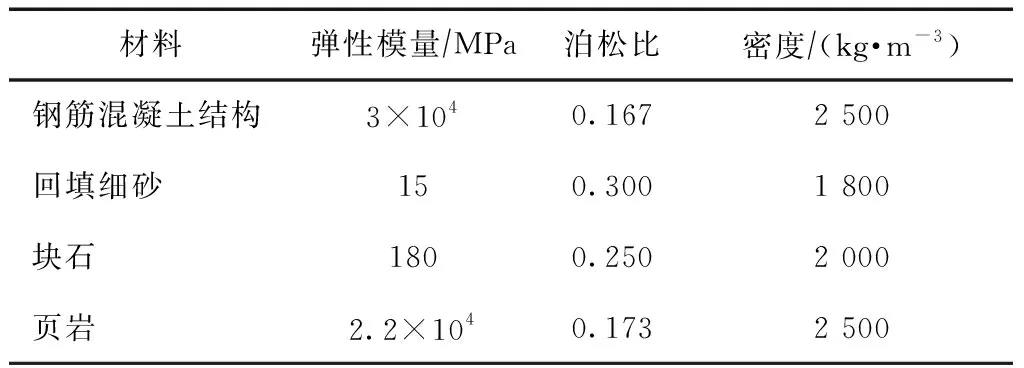
表1 材料參數

圖1 概化模型

2 工作原理

2.1 卸荷板工作原理

圖2a)、b)分別為碼頭結構與周圍土體整體變形等高線圖和變形矢量圖。從圖2a)可知，碼頭結構整體繞卸荷板面向墻后轉動，卸荷板整體繞碼頭前端向下轉動，卸荷板懸臂段底面與下側土體之間產生分離；從圖2b)可知，卸荷板和周圍土體同步向下移動，上墻(胸墻)與周圍土體同步向右(后)下方移動，下墻(空心方塊)與周圍土體共同向左(前)下方移動。圖2c)為碼頭墻背土壓力與墻底反力數值分析值和公式計算值對比。表2為土壓力、抗滑力和彎矩數值分析值差值。

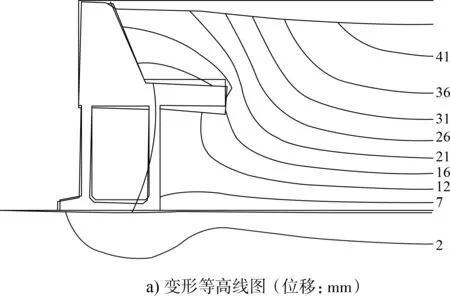
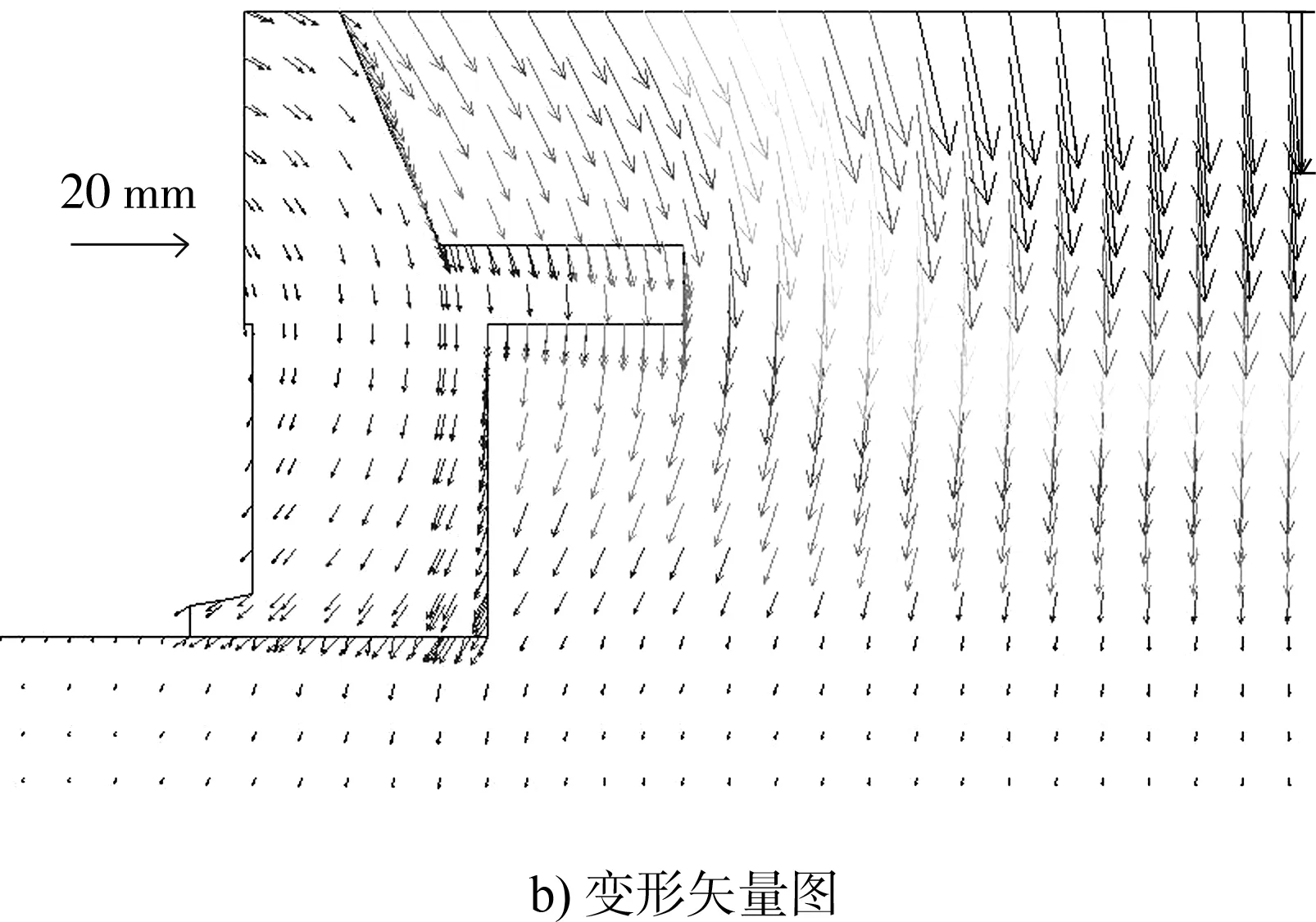
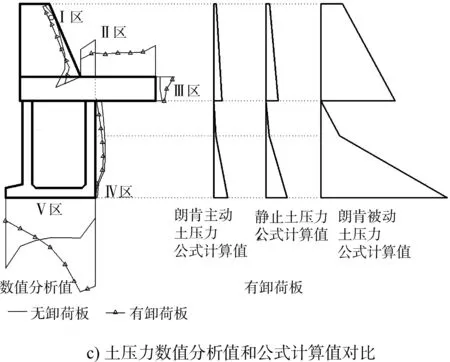
圖2 結構與土體整體變形和土壓力分布

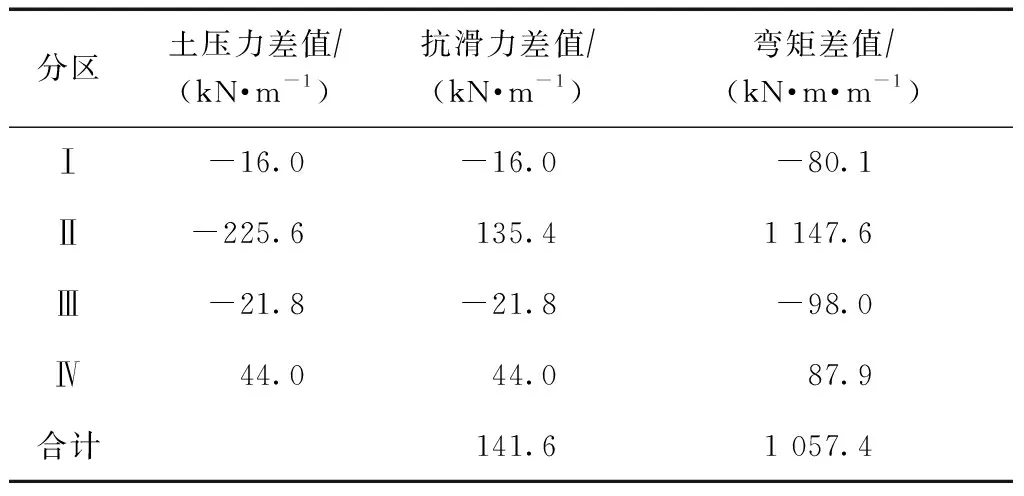
表2 土壓力、抗滑力和彎矩數值分析值差值

從圖2c)和表2可知：1)與無卸荷板相比，有卸荷板數值分析值Ⅰ～Ⅲ區的土壓力較大；Ⅳ區土壓力值較小；Ⅴ區地基反力值后鍾段大于前趾段。2)有卸荷板墻背土壓力數值分析值和公式計算值比較可知，Ⅰ區和Ⅲ區土壓力值大于主動和靜止土壓力公式計算值，小于被動土壓力公式計算值；Ⅳ區土壓力值與主動土壓力公式計算值接近。

從圖2和表2可知，組合懸臂式卸荷板構件后，碼頭結構重心整體后移，卸荷板上部回填料自重、面上堆載和懸臂段自重使卸荷板整體繞碼頭前端向下轉動，碼頭胸墻、空心方塊構件由于和卸荷板為一個整體，于同方向產生響應，最終表現為整體繞卸荷板面向墻后轉動的變形模式，這與無卸荷板重力式碼頭最可能發生繞墻底前趾轉動的變形模式存在明顯差別。由于卸荷板懸臂段向下位移受到限制，而其下部土體向下位移較大，從而形成懸臂段對下部土體的遮簾(卸荷)效果，減少了下墻墻后側向土壓力，但與之對應，上墻往墻后位移擠壓后側土體，形成被動壓力區，增大了上墻墻后側向土壓力。

2.2 墻背土壓力分析

從上述分析和變形、土壓力數值分析分布圖、表對比可知，墻背土壓力分布與碼頭結構整體變形密切相關，有卸荷板工況下，受上墻產生被動壓力區影響，墻背Ⅰ區、Ⅲ區土壓力相對較大，土壓力增大率達到了40.2%，且介于靜止和被動土壓力公式計算值之間，按主動土壓力公式計算值乘以1.5的系數比較符合實際情況；下墻與后側土體形成主動卸荷區，Ⅳ區土壓力曲線整體表現為兩頭小、中間大的分布形式，數值分析值與主動土壓力公式計算值比較接近，并表現出明顯的卸荷效應，卸荷效率達到35.4%；與下墻整體向后轉動的位移同步，墻底地基反力表現為后踵附近大于前趾附近，表明組合卸荷板可調節下墻地基應力的分布，但是卸荷板懸臂長度太長或地面荷載過大也容易造成墻體后鍾應力過大。

2.3 碼頭結構整體穩定性分析

2.3.1抗滑作用影響程度

Ⅰ區和Ⅲ區對碼頭底面形成的滑動力合計增加了37.8 kNm，Ⅳ區和Ⅱ區對碼頭底面形成的抗滑力分別增加了44.0 kNm和135.4 kNm；卸荷板懸臂段自重對碼頭底面形成的抗滑力增加了37.5 kNm。上墻側向土壓力增大、下墻側向土壓力減小、卸荷板上方填料自重(包含地面堆載)增加和懸臂段自重增加對碼頭抗滑穩定性的貢獻率分別為-21.1%、24.6%、75.6%和20.9%。

2.3.2抗傾作用影響程度

Ⅰ區和Ⅲ區對碼頭前趾形成的傾覆力矩合計增大178.1 kN·mm，Ⅳ區和Ⅱ區對碼頭前趾形成的穩定力矩分別增大87.9 kN·mm和1 147.6 kN·mm；卸荷板懸臂段自重對碼頭前趾形成的穩定力矩增大271.9 kN·mm。上墻側向土壓力增大、下墻側向土壓力減小、卸荷板上方填料自重(包含地面堆載)增加和懸臂段自重增加對碼頭抗傾穩定性的貢獻率分別為-13.4%、6.6%、86.3%和20.5%。

上述分析表明，組合卸荷板構件后，碼頭整體的抗滑和抗傾穩定性均得到大幅增強，上墻和下墻墻背側向土壓力的變化對墻背的作用效應相互抵消后，可認為墻背側向土壓力變化對碼頭穩定影響有限，帶卸荷板碼頭整體穩定性之所以得到加強主要是依靠卸荷板上方填料自重(包含地面堆載)和懸臂段自重的增加。

3 卸荷板懸臂長度和位置的影響

3.1 卸荷板懸臂長度影響

圖3和表3分別為卸荷板不同懸臂長度下碼頭結構整體變形圖及土壓力、抗滑力和彎矩數值分析值。

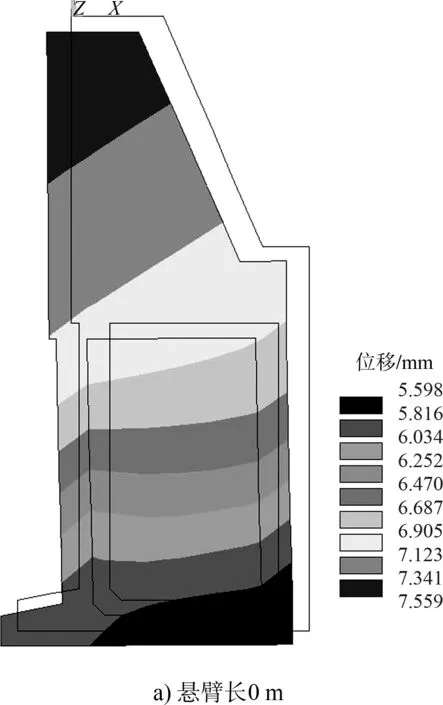
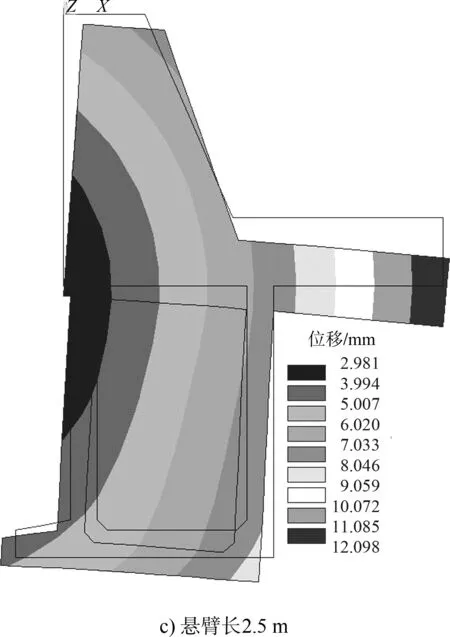
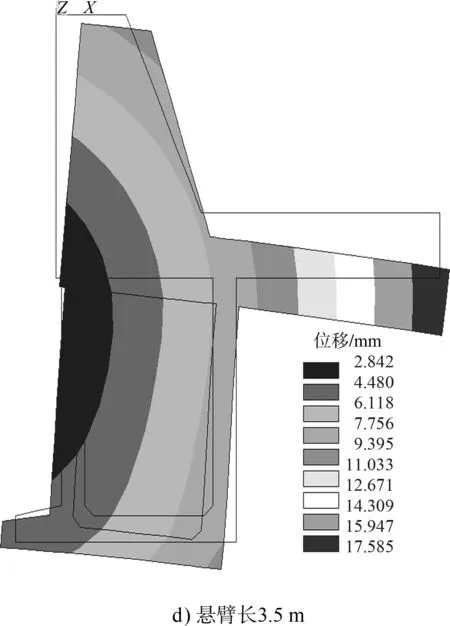
圖3 不同懸臂長度碼頭結構整體變形

表3 卸荷板不同懸臂長度下墻背土壓力、抗滑力和彎矩

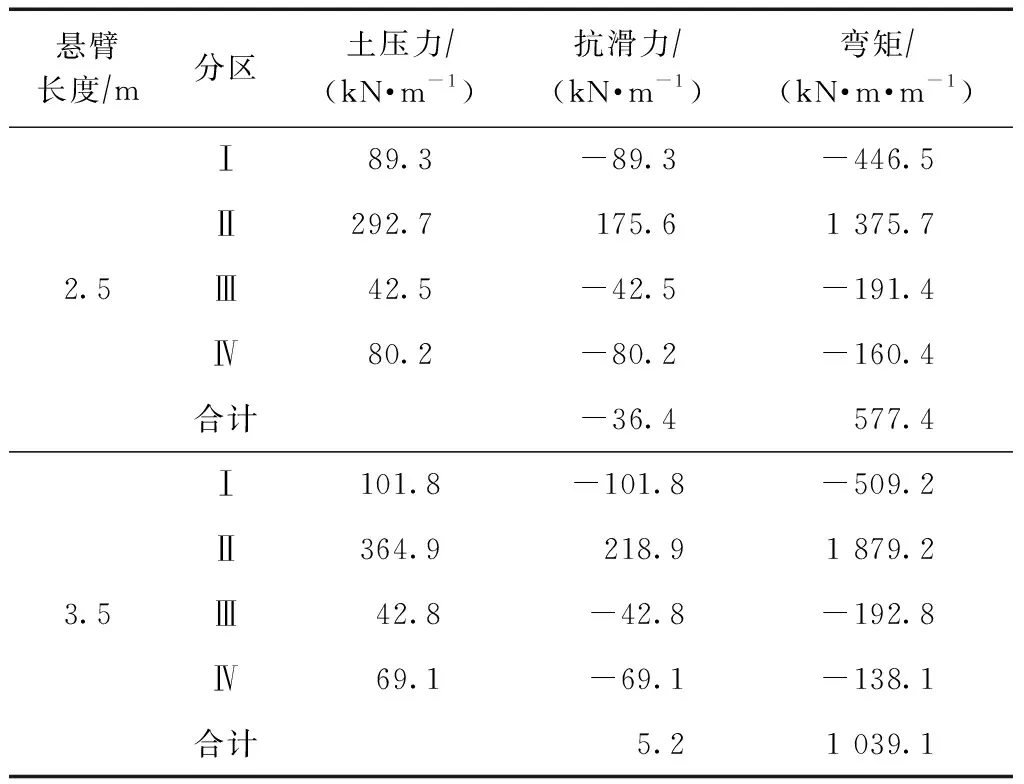
續表3

從圖3 和表3 可知：

1)隨著卸荷板懸臂長度增大，碼頭整體變形從繞墻底前趾向墻前轉動逐漸轉變為繞卸荷板向墻后轉動；

2)隨著卸荷板懸臂長度增加，碼頭整體向墻后轉動的幅度逐漸增大，碼頭結構抗滑和抗傾穩定性逐漸增強，抗滑力增幅前期存在明顯衰減，后期和穩定力矩增幅均逐漸趨于穩定。

3.2 卸荷板位置影響

圖4和表4分別為卸荷板不同位置下碼頭結構整體變形圖及土壓力、抗滑力和彎矩數值分析值。

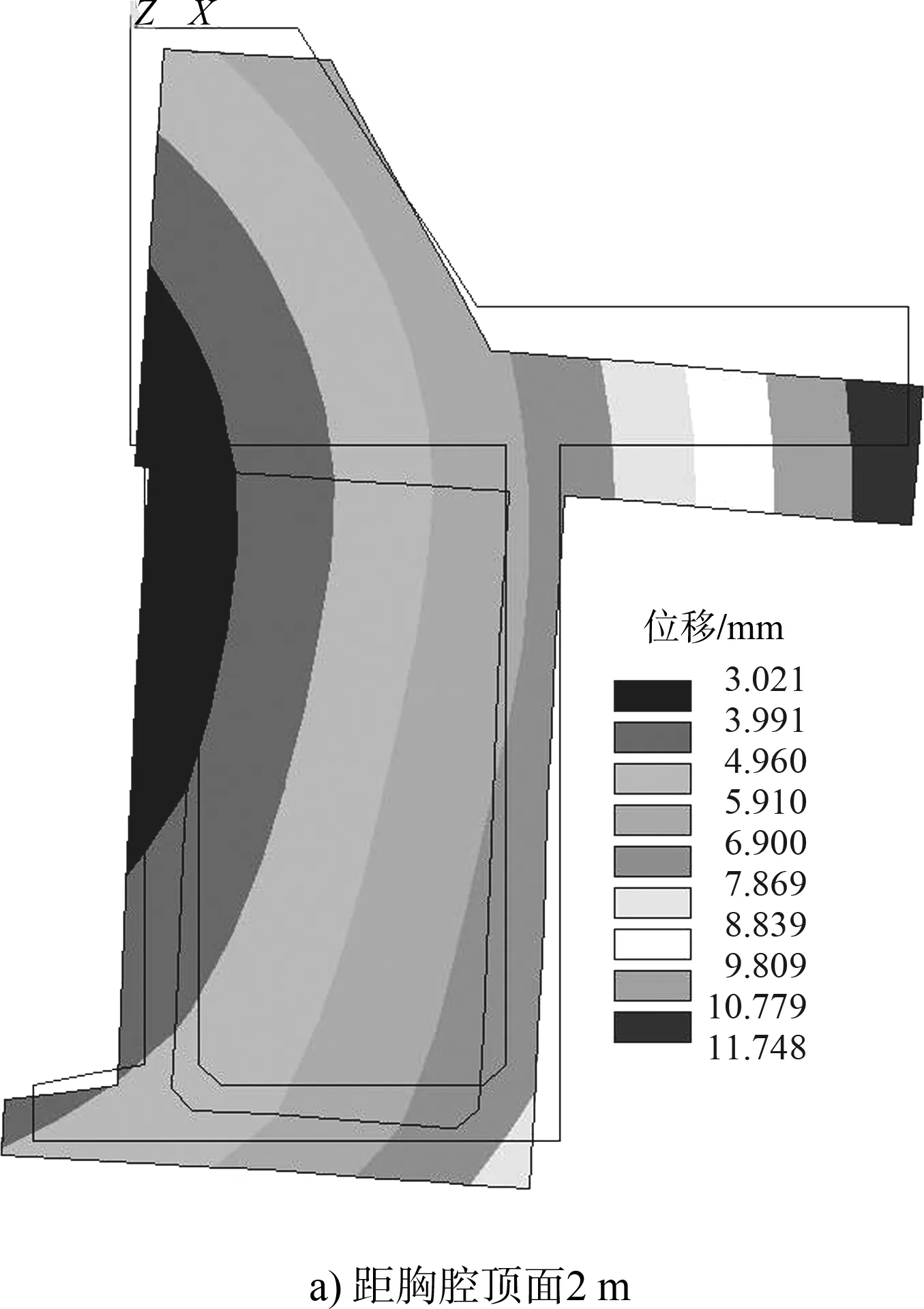
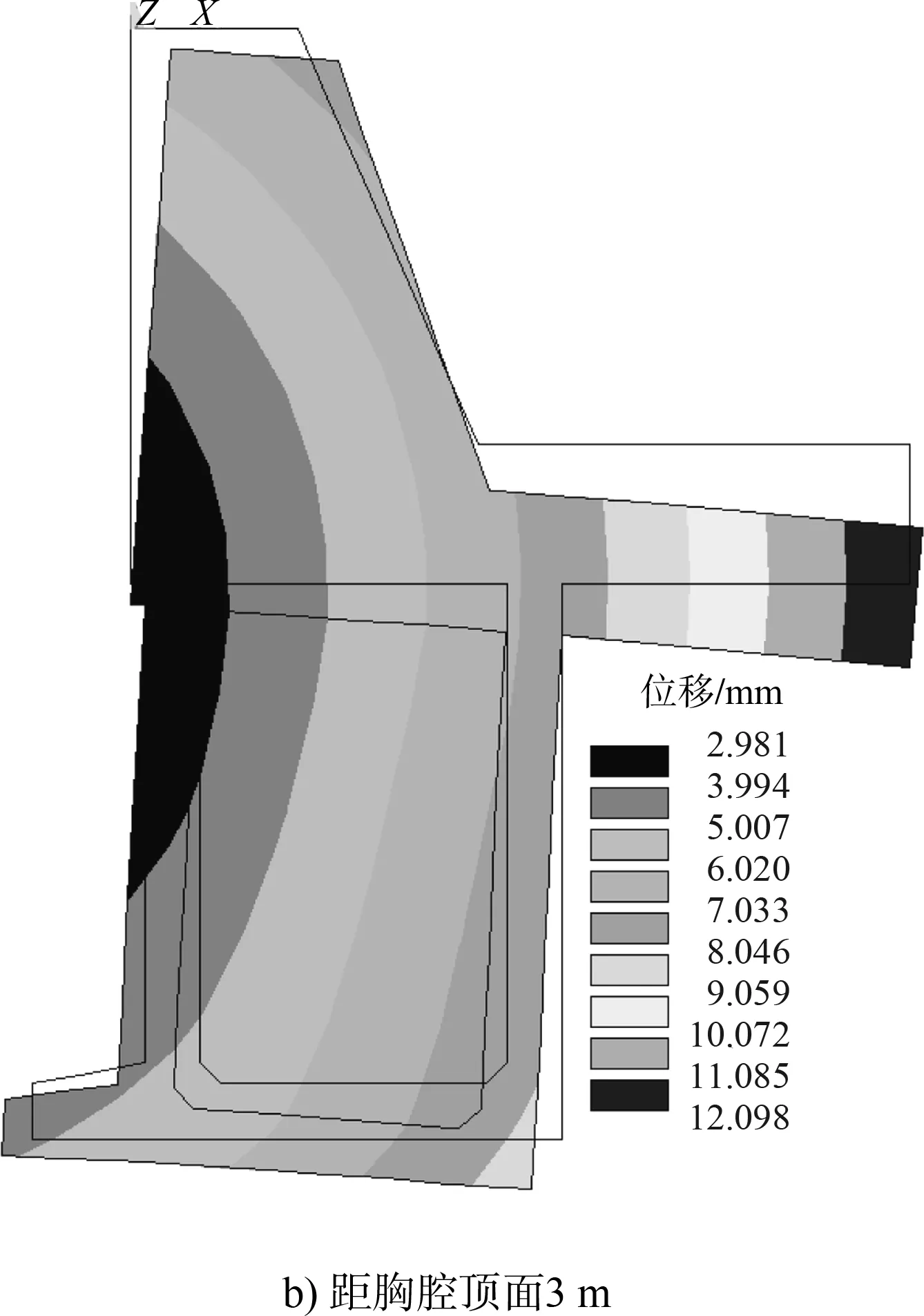
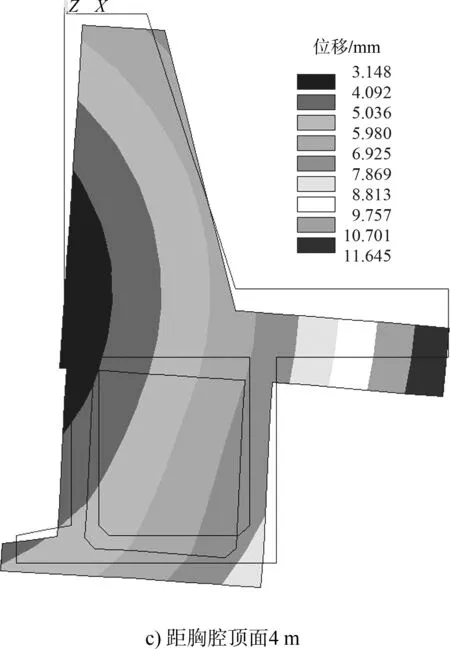
圖4 卸荷板不同位置碼頭結構整體變形

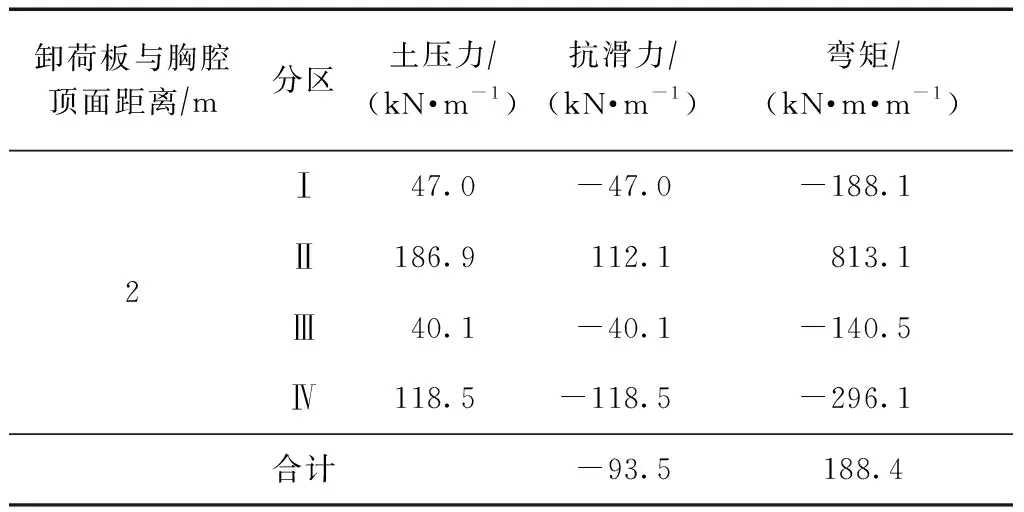
表4 卸荷板與胸腔頂面距離不同位置下墻背土壓力、抗滑力和彎矩

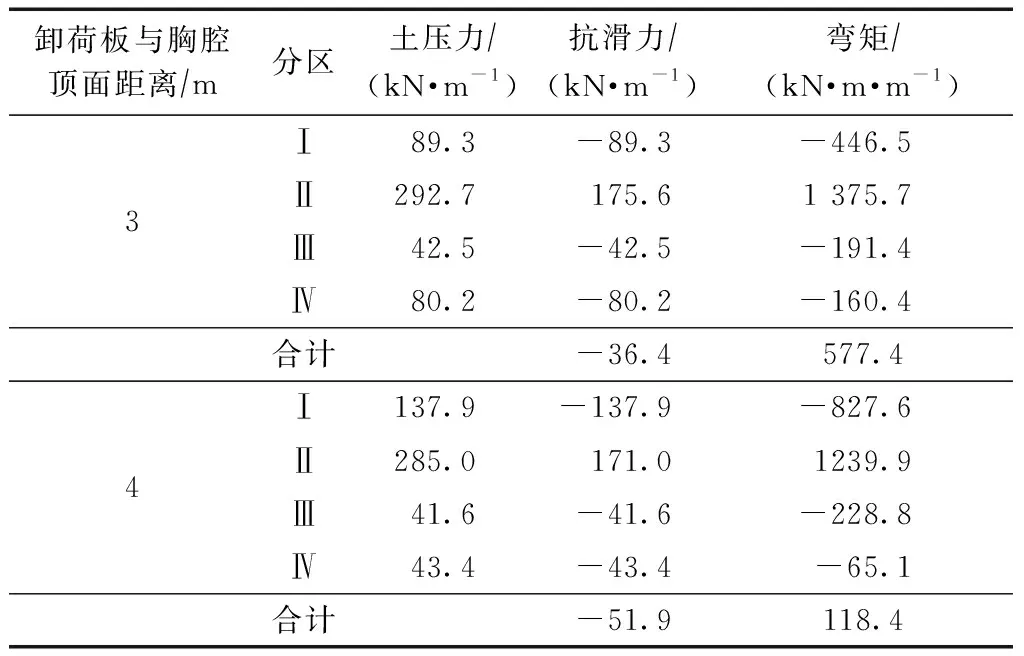
續表4

可以看出：

1)隨著卸荷板位置從上往下移動，碼頭整體的變形幅度基本一致；

2)碼頭整體抗滑和抗傾穩定性隨卸荷板位置從上向下先增強后減弱，最佳位置在約0.6倍墻高處。

4 結論與建議

1)帶卸荷板碼頭整體表現為繞卸荷板向墻后轉動的變形模式，與無卸荷板重力式碼頭常見的繞墻底前趾轉動的變形模式存在差別。

2)墻背土壓力整體分布與碼頭整體變形同步，上墻往墻后位移擠壓后側土體，形成被動壓力區，墻背土壓力增大率為40.2%，下墻往墻前位移形成主動卸荷區，墻背土壓力卸荷效率為35.4%，兩者相互抵消，可知側向土壓力變化對碼頭結構整體穩定影響有限。

3)上墻數值分析墻背土壓力可按朗肯主動土壓力公式乘以1.5的增大系數計算，下墻數值分析墻背土壓力可直接按朗肯主動土壓力公式計算。

4)上墻側向土壓力增大、下墻側向土壓力減小、卸荷板上方填料自重(包含地面堆載)增加和懸臂段自重增加對碼頭抗滑穩定性的貢獻率分別為-21.1%、24.6%、75.6%和20.9%；對碼頭抗傾穩定性的貢獻率分別為-13.4%、6.6%、86.3%和20.5%，后兩者是主要貢獻因素。

5)碼頭結構整體抗滑和抗傾穩定性隨卸荷板懸臂長度增強。

6)碼頭結構整體抗滑和抗傾穩定性隨卸荷板位置從上往下先增強后減弱，最佳位置在0.6倍墻高左右。