RC框架-HPFRC耗能墻結構側向剛度計算模型

楊鵬輝, 梁興文, 何 偉, 辛 力

(1.西安建筑科技大學 建筑設計研究院， 陜西 西安 710055; 2.西安建筑科技大學 土木工程學院, 陜西 西安 710055; 3.中國啟源工程設計研究院有限公司, 陜西 西安 710018; 4.中國建筑西北設計研究院有限公司, 陜西 西安 710018)

高性能纖維增強混凝土(HPFRC)具有拉伸應變硬化和多裂縫穩定開展等性能,是理想的耗能材料[1-2].將HPFRC耗能墻裝配于鋼筋混凝土(RC)框架結構中,形成RC框架-HPFRC耗能墻新型抗震結構.梁興文等[3]采用擬靜力試驗研究了這種結構模型的破壞過程、破壞機理、滯回性能、強度退化、剛度退化及耗能能力等特性,結果表明：HPFRC耗能墻可以提高RC框架結構的延性和耗能能力;在罕遇地震作用下,RC框架-HPFRC耗能墻結構僅產生中度損傷;在同一級水平荷載作用下,RC框架與HPFRC耗能墻的損傷程度不同,導致2種構件的截面剛度退化不同步.為明確該結構在水平荷載作用下的基本力學性能,需要分別確定RC框架和HPFRC耗能墻在同一級水平荷載作用時的有效側向剛度,再將兩者的有效側向剛度按一定的方法進行組合,從而可以得到這種結構的有效側向剛度.

本文根據2個完全相同的單層、單跨RC框架內分別裝配1、2片HPFRC耗能墻所組成的試件FW-1和FW-2的擬靜力試驗結果[3],并結合其他相關文獻的試驗研究結果,確定RC框架以及HPFRC耗能墻的剛度退化規律;在此基礎上,研究RC框架-HPFRC 耗能墻結構在開裂荷載點、屈服荷載點和峰值荷載點的有效側向剛度計算模型;最后針對本文的2個試件,用本文所提模型計算的位移值與試驗位移值進行對比.

1 RC框架-HPFRC耗能墻結構剛度退化規律

1.1 框架結構剛度退化系數

國內外學者對RC框架結構的剛度退化問題已做過較多研究,日本學者武藤清[4]對兩層一跨RC框架模型進行試驗研究,得到框架結構在水平荷載作用下的剛度退化規律,如圖1所示.圖中β為框架剛度退化系數(在任一加載點時的割線剛度與初始剛度的比值);θ為框架的層間側移角.近年來很多學者在研究RC框架結構的抗震性能時,采用單層、單跨RC框架作為試驗對比[5-16],得到了單層、單跨RC框架割線剛度的退化規律.通過對文獻[5-16]中13榀單層、單跨RC框架試驗數據進行分析,得到試件屈服點割線剛度與開裂點割線剛度比值的平均值為0.54.由圖1可見：當位移角為1/136(試驗屈服位移角平均值)時,剛度退化系數為0.50,驗證了該規律的可靠性.

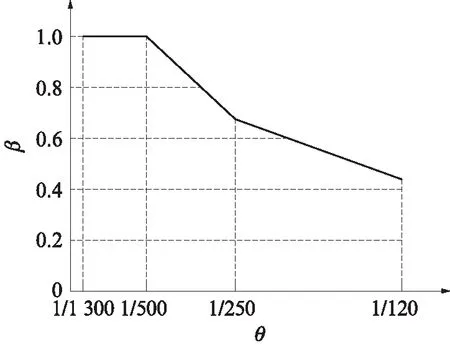
圖1 框架各變形階段剛度退化Fig.1 Stiffness degradation at various deformation stages

計算平面及豎向均規則的RC結構地震反應時,可將其等效為單自由度體系.Rosenblueth[17]將實際力-位移關系簡化為雙線性力-位移關系,得到：

(1)

式中：Keff為等效剛度,取最大位移對應的割線剛度,即試件峰值點對應的割線剛度;K0為彈性剛度,因該方法采用雙線性力-位移關系,忽略了開裂點的相關特征,即K0實際為結構屈服點對應的割線剛度;α為屈服后剛度與初始彈性剛度之比為;μ為位移延性需求,其值為試件峰值位移μmax與屈服位移μy的比值.

Keff/K0實際反映了試件峰值點相對于屈服點的剛度退化程度.通過對文獻[5-16]中的數據進行分析,取α為0.1,計算得到13榀單層、單跨RC框架峰值點割線剛度與屈服點割線剛度的比值Keff/K0的平均值為0.46.由框架屈服點的剛度退化系數,可以得到單層、單跨RC框架峰值點相對于開裂點的剛度退化系數為0.25.

綜上,得到單層、單跨RC框架剛度退化規律如圖2所示.

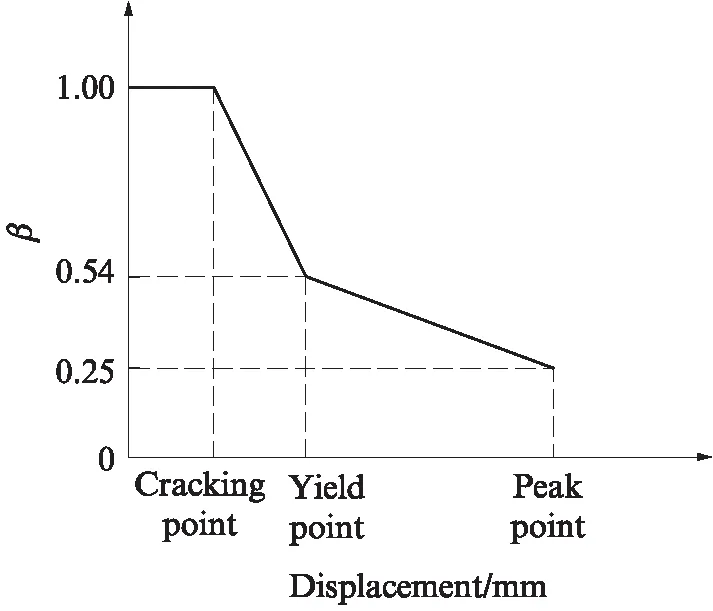
圖2 單層、單跨RC框架剛度退化規律Fig.2 Stiffness degradation regularity of single-story and single-span RC frame

1.2 HPFRC耗能墻剛度退化規律

根據試件FW-1和FW-2的試驗現象[3],分析HPFRC耗能墻暗柱受力縱筋應變可以發現,至試驗結束時,大多數暗柱縱筋的應變值接近但均未超過0.002.因此,可以認為試件達到極限承載力時,HPFRC耗能墻即將進入屈服階段,只需確定HPFRC耗能墻在自身屈服點之前的剛度退化情況.

試件開始加載時,HPFRC耗能墻截面剛度為彈性剛度EwIw;隨荷載的增加,耗能墻剛度會按一定規律退化,引入HPFRC耗能墻截面剛度折減系數αw,i,用以考慮耗能墻在不同加載階段側向剛度的折減,αw,i在不同受力階段的具體取值在后續各節中確定.

2 RC框架-HPFRC耗能墻結構各特征荷載點的側向剛度及位移計算

2.1 RC框架-HPFRC耗能墻結構剛度計算模型

在水平荷載作用下,RC框架與HPFRC耗能墻共同受力,協同變形.計算其側向剛度時,采用如下假定：

(1)RC框架-HPFRC耗能墻結構所承受的水平荷載由RC框架與HPFRC耗能墻共同承擔.

(2)因RC框架內僅局部裝配HPFRC耗能墻,故忽略RC框架與HPFRC耗能墻之間的擠壓等相互作用,假定這種結構在第i特征荷載點的側向剛度Ki等于相應特征荷載點RC框架側向剛度Kf,i與HPFRC耗能墻側向剛度Kw,i之和：

Ki=Kf,i+Kw,i

(2)

(3)由于HPFRC耗能墻與RC框架上、下梁通過鋼板連接件及螺栓連接,故RC框架梁與HPFRC耗能墻之間的連接約束條件不明確.為簡化分析,計算耗能墻的側向剛度時,假定HPFRC耗能墻隨RC框架梁僅產生相對水平平動變形,由此產生的誤差通過耗能墻剛度折減系數予以考慮.

(4)計算RC框架-HPFRC耗能墻結構各特征荷載點處的側向剛度時,RC框架與HPFRC耗能墻采用各自的剛度退化系數.設RC框架的側向剛度退化系數為βf,i,則Kf,i可表示為：

Kf,i=βf,i·Kf,e

(3)

式中：Kf,e為RC框架的彈性側向剛度.

同理,HPFRC耗能墻的側向剛度退化規律由剛度退化系數αw,i表達,則Kw,i可表示為：

Kw,i=αw,i·Kw,e

(4)

式中：Kw,e為HPFRC耗能墻的彈性側向剛度.

2.2 RC框架-HPFRC耗能墻結構在開裂荷載點的有效側向剛度

2.2.1開裂荷載點RC框架與HPFRC耗能墻的受力狀態確定

當試件達到開裂狀態時,RC框架柱外側面出現可見的細微水平裂縫,HPFRC耗能墻墻面及側面均未出現可見裂縫[3].由此可認為,試件加載至開裂荷載點時,RC框架剛好達到開裂狀態,HPFRC耗能墻未達到開裂狀態.

2.2.2開裂荷載點RC框架的有效側向剛度

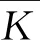
(5)

(6)

式中：Ec為混凝土的彈性模量;ib和ic分別為框架梁、柱的線剛度;Ib和Ic分別為框架梁、柱的截面慣性矩;Hc和L分別為框架柱的計算高度與梁的計算跨度.

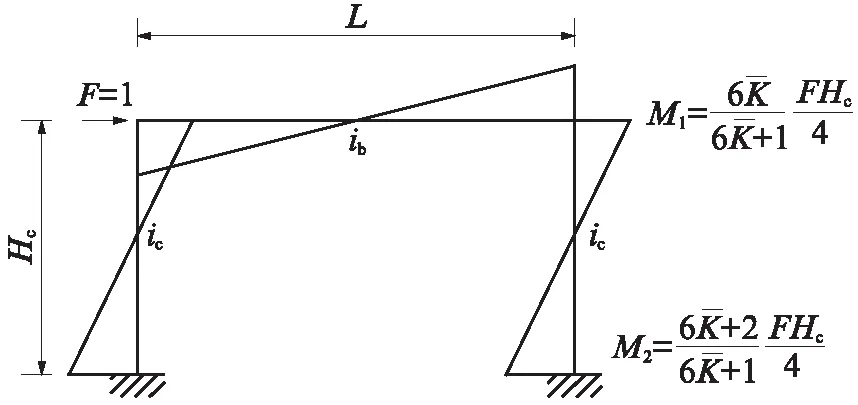
圖3 水平荷載作用下單層、單跨RC框架彎矩圖Fig.3 Bending moment diagram of single-story and single-span RC frame under horizontal load

由式(5)可得一根單層、單跨RC框架柱的彈性側向剛度Kc：

(7)

(8)

式中：αc為柱的側向剛度修正系數.

考慮到RC框架柱在開裂荷載點的截面剛度降低,參考相關文獻[18],其開裂點的有效側向剛度Kf,cr仍按式(7)計算,但其中EcIc需乘以系數0.8.對于本文試驗模型而言,其開裂點的側向剛度Kf,cr為：

Kf,cr=2Kc·αf,cr

(9)

式中：αf,cr為RC框架柱截面剛度折減系數,取0.8.

2.2.3開裂荷載點HPFRC耗能墻的有效側向剛度

在RC框架-HPFRC耗能墻結構加載至開裂點時,耗能墻未出現肉眼可見裂縫,故可認為耗能墻尚處于彈性階段,結構在開裂狀態時耗能墻的剛度等于相同約束條件下耗能墻的彈性側向剛度.HPFRC耗能墻通過鋼板連接件夾持,并通過高強度螺栓連接,施加到試件頂部的水平荷載通過墻與梁之間的鋼板連接件及高強度螺栓傳遞到耗能墻頂部.為便于裝配耗能墻,HPFRC耗能墻與鋼板連接件之間、高強度螺栓與螺栓孔之間均留有空隙,故試驗加載初期連接鋼板與耗能墻內嵌鋼板之間產生滑移,從而降低了HPFRC耗能墻提供給試件的側向剛度,如圖4所示.在加載后期,由于HPFRC耗能墻上、下兩端螺栓孔處的應力集中,使耗能墻局部損傷,耗能墻上、下兩端產生轉角,降低了其側向剛度,如圖5所示.考慮以上因素對HPFRC耗能墻側向剛度產生的削弱作用,引入滑移轉角影響系數λ,用以考慮連接件鋼板與耗能墻內嵌鋼板之間的滑移以及耗能墻兩端轉動對耗能墻側向剛度的影響.在荷載控制加載階段,未觀察到HPFRC耗能墻因轉角引起的連接件鋼板與墻體的滑移;在位移控制加載階段,可明顯觀察到兩者間因轉角引起的相對滑移.因此可以認為,在試件屈服前,λ主要由連接件鋼板與耗能墻內嵌鋼板之間的水平相對滑移引起,λ取0.45;試件屈服時及屈服后,λ主要由耗能墻上、下兩端轉動引起,λ取0.15.

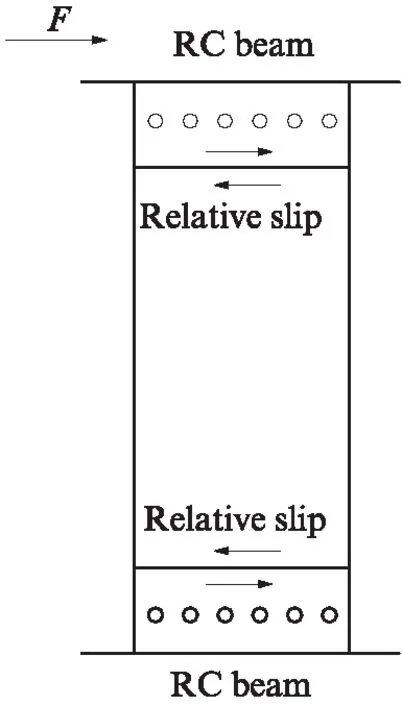
圖4 連接件與耗能墻內嵌鋼板相對滑移Fig.4 Relative slip between connectors and embedded plate of energy dissipation wall

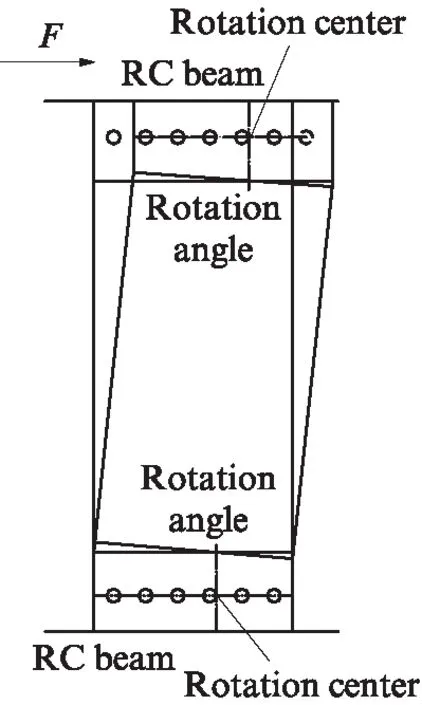
圖5 耗能墻上、下兩端轉動Fig.5 Rotation of two ends of energy dissipation wall

考慮到HPFRC耗能墻在不同加載階段截面剛度的下降,須引入截面剛度折減系數αw,i.裝配于RC框架結構中的HPFRC耗能墻,在水平荷載作用下,其上端隨框架梁產生水平平移,與兩端僅產生相對平移的連梁(試驗中模擬連梁兩端僅產生相對平移)的受力狀態相似,故可用本課題組之前測試的HPFRC連梁的試驗結果[19-20],即用HPFRC 連梁的剛度退化系數來確定本文HPFRC耗能墻的剛度退化系數.經統計分析文獻[19-20]的試驗結果,可得HPFRC耗能墻各受力階段截面剛度折減系數αw,i的取值如下：耗能墻開裂前處于彈性階段,αw,i值可取為0.8;墻體在開裂荷載點處的αw,i值可取為0.55;墻體在屈服荷載點,αw,i值可取為0.40.

由于HPFRC耗能墻的高寬比相對較小,其剪切變形引起的側移不宜忽略;引入滑移轉角影響系數λ和截面剛度折減系數αw,i后,HPFRC耗能墻在開裂荷載點的有效側向剛度Kw,cr為：

(10)

式中：Hw為HPFRC耗能墻的高度;Ew為HPFRC材料的彈性模量;Gw為HPFRC材料剪切模量,取0.4Ew;Iw和Aw分別為HPFRC耗能墻的截面慣性矩和截面面積;k為截面形狀系數,對矩形截面取1.2;λ為滑移轉角影響系數,根據試驗結果,取0.45;αw,cr為RC框架-HPFRC耗能墻結構在開裂荷載點時HPFRC耗能墻的截面剛度折減系數,取0.8;n為耗能墻的數量.

2.2.4開裂剛度及開裂位移

根據式(2),RC框架-HPFRC耗能墻結構開裂點的有效側向剛度Kcr為：

Kcr=Kf,cr+Kw,cr

(11)

RC框架-HPFRC耗能墻結構的開裂位移Δcr為：

(12)

式中：Fcr表示RC框架-HPFRC耗能墻結構開裂點處的水平荷載.

2.3 RC框架-HPFRC耗能墻結構在屈服荷載點的有效側向剛度

2.3.1屈服荷載點RC框架與HPFRC耗能墻受力狀態確定

由試驗現象可知,當試件加載至屈服荷載點時,框架柱縱向受力鋼筋屈服,耗能墻暗柱的縱向受力鋼筋均未達到屈服應變,且耗能墻墻面上未出現明顯的裂縫.由此可認為試件加載至屈服荷載點時,框架柱剛好達到屈服極限狀態,HPFRC耗能墻未達到開裂狀態.

2.3.2屈服荷載點RC框架的有效側向剛度

RC框架-HPFRC耗能墻結構在屈服荷載點時,RC框架剛好達到屈服極限狀態,則由式(3)可得RC框架的有效側向剛度Kf,y：

Kf,y=βf,y·Kf,e

(13)

式中：βf,y為RC框架屈服點的剛度退化系數,由圖2可知,該值取0.54.

2.3.3屈服荷載點HPFRC耗能墻的有效側向剛度

試件加載至屈服荷載點時,耗能墻未出現裂縫;試件屈服后的下一級加載,耗能墻出現大量裂縫.表明試件加載至屈服荷載點時,HPFRC耗能墻雖未觀察到肉眼可見的裂縫,但已不再處于彈性階段.根據式(4),此時HPFRC耗能墻的有效側向剛度Kw,y由式(14)計算：

(14)

式中：αw,y為RC框架-HPFRC耗能墻結構在屈服荷載點時HPFRC耗能墻的剛度折減系數,考慮到該狀態下HPFRC耗能墻未開裂但接近開裂,其取值為0.55;滑移轉角影響系數λ取0.15.

2.3.4屈服剛度及屈服位移

根據式(2),RC框架-HPFRC耗能墻結構在屈服荷載點的有效側向剛度Ky為：

Ky=Kf,y+Kw,y

(15)

RC框架-HPFRC耗能墻結構的屈服位移Δy為：

(16)

式中：Fy表示RC框架-HPFRC耗能墻結構屈服點的水平荷載.

2.4 RC框架-HPFRC耗能墻結構在峰值荷載點的有效側向剛度

2.4.1峰值荷載點RC框架與HPFRC耗能墻受力狀態的確定

在峰值荷載點的前一級加載下,僅右柱外側角部混凝土保護層開始有被壓酥的跡象;試件加載至峰值荷載時,左、右兩柱外側面及左柱內側面混凝土均被壓碎,保護層脫落,表明柱底受壓區邊緣混凝土已達到其極限壓應變,框架柱底截面已至最大承載力,此時HPFRC耗能墻有大量裂縫產生,但暗柱縱筋未屈服.故認為RC框架-HPFRC耗能墻結構加載至峰值荷載點時,RC框架剛好達到最大承載力,HPFRC耗能墻已超過開裂極限狀態,但未達到屈服極限狀態.

2.4.2峰值荷載點RC框架的有效側向剛度

在RC框架-HPFRC耗能墻結構中,由于HPFRC耗能墻的存在,增加了RC框架在屈服后的延性,使結構中RC框架的峰值位移滯后于單層、單跨RC空框架的峰值位移,故考慮框架峰值位移滯后的影響,須引入位移延性影響系數η.通過對文獻[5-16]中的數據分析,可得13榀單層、單跨RC空框架位移處性需求μ的平均值為2.77.本文試件中RC框架位移處性需求μ的平均值為3.83.由數據對比可得到,試件峰值荷載點割線剛度與單層、單跨RC空框架峰值點割線剛度的比值為0.72,故可將位移延性影響系數η取為0.7.

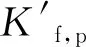
(17)

式中：Kf,p為單層、單跨RC空框架峰值點割線剛度;βf,p為單層、單跨RC空框架峰值點剛度退化系數,由圖2可知,該值取0.25.

2.4.3峰值荷載點HPFRC耗能墻的有效側向剛度

當RC框架-HPFRC耗能墻結構加載至峰值荷載點時,HPFRC耗能墻已超過開裂極限狀態,未達到但接近屈服極限狀態.試件加載至峰值荷載點時,HPFRC耗能墻的截面剛度折減系數為αw,p,則此時HPFRC耗能墻的有效側向剛度Kw,p為：

(18)

式中：滑移轉角影響系數λ取0.15;剛度折減系數αw,p取0.40.

2.4.4峰值荷載點的有效側向剛度及位移

根據式(2),RC框架-HPFRC耗能墻結構在峰值荷載點的有效側向剛度Kp為：

(19)

RC框架-HPFRC耗能墻結構峰值荷載點的位移Δp為：

(20)

式中：Fp表示RC框架-HPFRC耗能墻結構峰值點的水平荷載.

2.5 計算結果與試驗結果的對比

試件特征荷載點所對應的RC框架與HPFRC耗能墻的受力狀態如表1所示.在確定試件各特征點的受力狀態后,采用側向剛度和位移計算公式,根據文獻[3]中表3的相關數據,計算得到試件在頂部水平荷載作用下開裂荷載點、屈服荷載點和峰值荷載點的位移,特征荷載點位移的計算值與試驗值對比如表2所示.由表2可見：各特征荷載點位移計算值與試驗值吻合較好,表明本文的剛度計算模型較為合理.

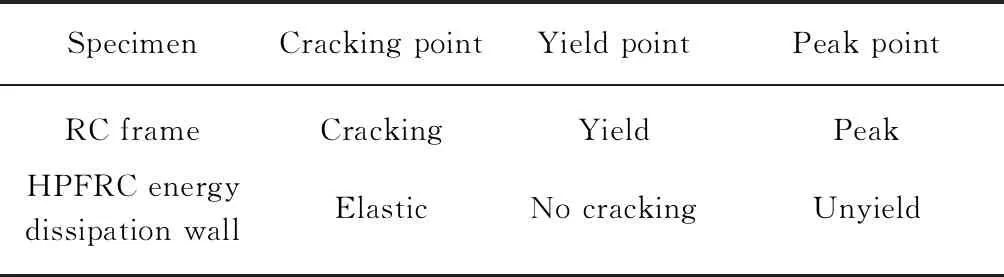
表1 試件特征荷載點對應的RC框架與HPFRC耗能墻的受力狀態Table 1 Stress state of RC frame and HPFRC energy dissipation wall at characteristic load points

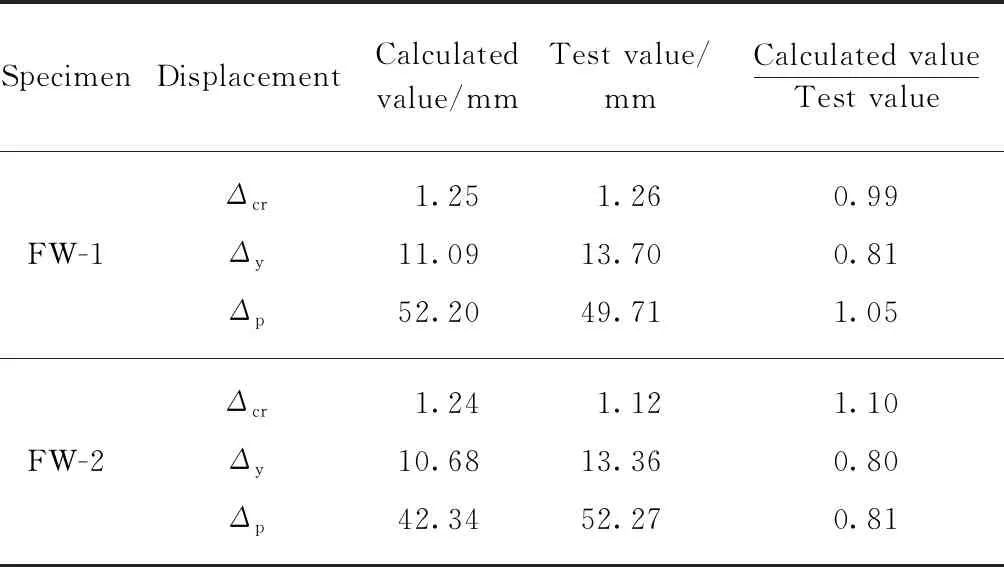
表2 特征荷載點位移計算值與試驗值對比Table 2 Comparison between calculated value and experimental results of lateral displacement at characteristic load points

3 結論

(1)RC框架-HPFRC耗能墻結構中的RC框架與HPFRC耗能墻是由性能差異較大的材料制作,故在相同的特征荷載點(如開裂、屈服、峰值等荷載點)處,2種構件的損傷狀態和剛度退化程度明顯不同,HPFRC耗能墻比RC框架的剛度退化緩慢很多.計算這種結構的水平承載力和側向剛度時,應考慮這種差異.

(2)RC框架-HPFRC耗能墻結構中RC框架的剛度退化規律,主要取決于結構的受力狀態和材料性能退化;而HPFRC耗能墻的剛度退化規律除與結構的受力狀態和材料性能退化有關外,尚與耗能墻上、下端和框架梁的連接構造有關.因此,本文提出的HPFRC耗能墻在各特征荷載點的剛度折減系數,僅適用于本文的連接構造情況.

(3)基于RC框架和HPFRC耗能墻的剛度退化規律建立的有效側向剛度計算模型,基本上反映了這種結構的受力和變形特點,按此模型所得的結構位移計算值與試驗值基本吻合.但由于試驗數據較少,本文方法的可靠性有待進一步試驗驗證.