基于標簽傳播的拓撲勢社區檢測算法①

費 蓉,李莎莎,胡 博,唐 瑜,方金正

1(西安理工大學 計算機科學與工程學院,西安 710048)

2(北京華電優控科技有限公司,北京 100193)

眾多復雜系統都可抽象成為網絡模型,如計算機網絡、信息網絡、社會網絡和生物網絡等得到了廣泛應用[1],社區檢測問題對于研究復雜網絡以及人類生活具有重要意義.社區檢測期望將鏈接最緊密的節點劃分至同一社區,有助于更好地了解整個社交網絡,進而有效利用資源[2].現實中,Facebook 等以朋友關系為基礎的社交網絡上,通過社區檢測可進行朋友推薦[3,4].另外也可以用社區檢測對具有鏈接關系并且同興趣的用戶進行興趣推送[5].除此之外,還可用于交通網絡中分析交通對城市功能社區(商業區、居民區、學校等)分布之間的關系[6].

近年來,社區檢測問題常歸于以下類型:基于圖分割的社區檢測,需要提前定義分割社區個數及體積,通過最小化社區間的鏈接邊的數量實現社區劃分,如Kemighan-Lin 算法和譜劃分算法;基于聚類的社區檢測則是通過節點間的關系利用聚類的思想將其進行社區檢測,以GN 算法[7]、Newman 貪心算法和k-means算法為代表;基于模塊度最大化的社區檢測如Louvain算法,利用模塊度獲取最優的網絡社區劃分;基于非負矩陣的社區檢測,利用非負矩陣的思想將節點的鏈接矩陣進行分解得到節點社區歸屬矩陣,如LANMF 算法[8];基于標簽的社區檢測算法,以LPA 算法、CORP算法和LPPB 算法等為代表,對每個節點隨機生成標簽,逐輪刷新所有節點的標簽,直到所有節點的標簽不再發生變化為止.

節點拓撲勢的概念源于認知物理學中的數據場理論[9],2009年,淦文燕提出了一種基于拓撲勢的社區檢測方法,利用節點的鏈接信息構造拓撲勢場,在拓撲勢場內進行社區劃分[10].拓撲勢原理近年來得到了長足的發展.2018年,Wang 在山谷結構的拓撲勢場下基于節點位置進行分析,設計DOCET 算法[11].但拓撲勢社區算法在實踐中存在一種現象,當獲得的模塊度值較高時,社區的劃分數量過大,當社區網絡過于復雜時,真實數據集出現了很多孤立性節點或孤立性小社區.基于拓撲勢原理進行社區劃分,存在大量3-4 節點孤立為一個社區的現象出現.這種孤立社區的出現為現實的推送,社區的擴大等帶來影響.近期研究顯示,社區劃分不再單純的考慮鏈接結構,而是通過增加節點的屬性信息進行社區劃分.節點的屬性信息越來越受到關注[12].

本文面向含標簽屬性的社區檢測問題,針對上述基于拓撲勢進行的社區劃分存在的孤立性社區問題,提出了一種結合屬性標簽的拓撲勢社區檢測算法(TPCDLP).首先,將結合標簽傳播思想將屬性信息構造出節點間的鏈接權值.其次,把鏈接權值加入到拓撲勢當中構造拓撲勢場.然后,利用核心節點進行子群社區的劃分.最后,利用子群社區間核心節點的距離進行社區劃分.

1 相關工作

李德毅等2008年提出了社區檢測中的拓撲勢理論,構造了一種在網絡拓撲空間中構造的虛擬勢場[8].拓撲勢借鑒了數學中的拓撲學和物理中的場論思想,將網絡G看作一個包含n個節點的及其相互作用的抽象系統.每一個結節周圍存在一個作用場,位于場中的任何節點都會收到其周圍節點的影響.但是節點的影響力隨著網絡距離的增加而快速衰減.

定義1.拓撲勢場.一個網絡G=(V,E),網絡所有節點vi,1≤i≤n都存在一個拓撲勢φ (vi),所有節點的拓撲勢相互作用從而構成拓撲勢場.

定義2.拓撲勢.給定網絡G=(V,E),其中V={v1,v2,···,vn} 為網絡節點,E={(vi,vj)|vi,vj∈V,i≠j}為節點邊集合,每個節點的拓撲勢計算公式如下:

其中,dij表示節點vi與節點vj之間的網絡距離或跳數.影響因子 σ是用于控制每個節點的影響范圍.m(vj)表示節點vj的質量,可以用來描述每個節點的固有屬性,但是通過相似研究,在本文設置為m(vj)=1.

本文首先利用了信息傳播的特性將節點的屬性結構In和鏈關系E轉換成節點間的鏈接權重關系R.隨后,利用拓撲勢將具有鏈接關系的網絡結構轉化成山脈形狀的拓撲勢域.其次,在山脈形狀的立體結構中找到局部最高點,由局部最高點出發進行子群社區的劃分.最后根據子群社區的分布情況,將子群社區進行合并得到社區的劃分結果C.

2 一種基于標簽傳播的拓撲勢社區檢測算法

2.1 節點間鏈接權值計算

拓撲勢算法利用的是鏈接關系構造拓撲勢場,未考慮結節間的屬性關系.社區的定義是將具有鏈接緊密程度的節點化為一個社區,但是結節間的屬性關系同樣會影響到社區劃分的質量和現實場景的應用.

本文利用節點間的屬性關系和鏈接關系構造節點間拓撲勢的環境影響因子rij,從而保證節點i和 節點j之間的拓撲勢能夠受到環境影響因子影響.公式如下:

借鑒標簽傳播的思想,計算標簽從節點vi傳播到節點vj的概率P(vi→vj),隨后令節點vi和節點vj的環境影響因子rij=P(vi→vj).

2.2 標簽傳播特性

定義3.節點影響力.設網絡G=(V,E)中每個節點vi都擁有一個影響力值,用In fi表示.由于大多網絡并不是連通圖,因此本文采用文獻[13]所提出LeaderRank算法,計算節點的LR 值.

LeaderRank 算法提到社交網絡不是一個強連通圖,所以引入一個節點g(Ground Node),與其他節點相互連接,使社交網絡變成一個強連通圖.LeaderRank 算法核心公式:

其中,aij表示節點j到節點i是否有鏈接,有為1,無為0;表示節點j的出度個數;N表示節點總個數;LRi(t)表示i節點在t時刻的得分;tc表示LRi(t)收斂的得分;表示tc時刻地節點的得分;LRi表示i節點最終的得分.

圖1是一個小社交網絡拓撲結構圖,一共有18 個節點,每個節點代表一個人,每個人都有一個興趣愛好,將興趣愛好分為兩類,并用兩種不同的圖標表示人們的興趣愛好.節點間的連線代表人們之間的關系.通過上述的公式,計算得到這個簡單的社交網絡數據集每個節點的節點影響力,如表1所示.

圖1 小社交網絡

表1 小社區網絡的節點影響力LR

定義4.傳播特性k.定義ki←j為標簽從節點j到節點i的傳播特性度量值.

該傳播特性是由節點vi和節點vj的節點影響力決定的.當LRi遠大于In fj時,ki←j≈1,說明vj的影響力較大,節點vi容易受節點vj的影響.反之,當LRj遠大于LRi時,ki←j≈0,說明vi的影響力較大,節點vi不容易受節點vj的影響.

以節點1、2、3 為例,已知LR1=0.762 913,LR2=0.915 51,LR3=1.068 08,根據定義4 的公式,可得:

節點1 的影響力LR1小于節點3 和節點4 的影響力.通過比較發現節點1 到節點2 的傳播特性要低于節點2 到節點1 的傳播特性,同樣的節點1 到節點3的傳播特性也低于節點3 到節點1 的傳播特性.由此,傳播特性值可以反映出影響力高的節點與影響力低的節點之間受影響程度的差異.

2.3 節點間的相似度計算

社會網絡不僅具有拓撲結構特征,而且網絡中節點的內在屬性也容易獲取,如C-DBLP 中的學者記錄都擁有研究方向、工作單位等信息,因此節點的屬性特征S(節點的相似度)包含兩部分:結構屬性S t和節點內在屬性In.

結構屬性:

節點內在屬性:

N(i)表示節點i的所有鄰居與節點i的集合.ini={in1,in2,···,inz}為 節點i的內在屬性集合,iniz是節點vi的第z個屬性值;z是內在屬性總個數.

圖1所示的社交網絡數據集中,節點1 和節點2 都有一個相同的鄰居節點3 和節點4,所以結構屬性節點1 和節點2 節點都有相同的興趣愛好,所以內在屬性Ln1,2=(1/2)×(1+1)=1.由此節點1 和節點2 間的屬性特征S1,2=0.577 35+1=1.577 35.同理,S1,3=1.516 40,S1,4=1.516 40.

2.4 節點間的傳播概率計算

定義5.標簽傳播概率(節點間的關聯強度,也就是邊的權值).節點j的標簽以概率P(i←j)傳 播到節點i,P(i←j)取 決于節點i和j的相似性度量Si,j、傳播特性度量ki←j和鄰接矩陣δ (i,j).

節點j到節點i的標簽傳播概率體現了標簽從節點j傳播到節點i的能力,也可以認為是節點j到節點i的有向邊的權值.由此可得,節點j到節點i的有向邊的權值:

由上述公式可以計算r12=S1,2×k1→2×δ(1,2)=1.577 35×0.465 892×1=0.734 87,r13=0.664 62,r14=0.664 63.由于節點的拓撲勢公式φ(vi)=可以先計算節點vi的如圖2所示,節點1 的=r12+r13+r14=0.734 87+0.664 62+0.664 63=2.064 12.節點1 到節點2 的標簽傳播概率決定了節點1 將信息傳遞到節點2 的能力強度,由此也決定了節點1 到節點2 節點的屬性信息和鏈接信息影響后拓撲勢變化.表2是將每個節點到鄰居節點的環境影響因子進行加和的結果.

圖2 小社交網絡的節點1 的環境影響因子

表2 小社交網絡的節點環境影響因子求和

表3是通過改進后的拓撲勢公式計算出圖1的社交網絡數據集的每個節點的拓撲勢值.并且將節點中拓普勢局部最高的節點用五角星標記在圖3中.

2.5 子群社區劃分

通過節點拓撲勢的計算,將網絡的鏈接結構轉變成山脈形狀的拓撲勢場.社區的劃分就如同山的劃分,山峰、山谷和斜坡,對應社區的核心節點、重疊節點以及內部節點.

定義6.核心節點.假設在一個社交網絡G=(V,E)中,其拓撲勢域G′=(V,E,?),Ni是節點vi的鄰居節點.?vj∈Ni,如果? (vi)>?(vj),則節點vi是拓撲勢域的局部最高點.

通過上述的定義,可以看出核心節點是局部最高點,也就是山峰節點.如果根據當前的核心節點進行社區劃分,將會影響社區劃分的質量和數量.由此,當前通過核心節點劃分的社區被稱為子群社區,后續需要進一步處理.圖3中五角星標識的節點為拓撲勢局部最高點,也就是當前子群社區的核心節點.

定義7.重疊節點.假設在一個社交網絡G=(V,E)中,其拓撲勢域G′=(V,E,?),Ni是節點vi的鄰居節點.?vj∈Ni,如果? (vi)

當山谷節點就直接歸屬于它鄰居節點所在的社區.由此,山谷節點i處在兩個不同核心節點的社區之間,才能被稱為重疊節點.

定義8.內部節點.假設在一個社交網絡G=(V,E)中,其拓撲勢域G′=(V,E,?),Ni是節點vi的鄰居節點.內部節點滿足下面任意一種情況成立:(1)?vj∈Ni,如果?(vi)?(vj),則節點vi處于斜波位置,也就是拓撲勢域的內部節點.(2)如果?(vi)

定義9.邊緣節點.假設在一個社交網絡G=(V,E)中,其拓撲勢域G′=(V,E,?),Ni是節點vi的鄰居節點,Coverlap是重疊節點的集合,Cno?overlap是不重疊節點的集合.(1)如果vi∈Coverlap,則節點vi是邊緣節點;(2)?vj∈Nj,如果vi∈Cno?overlap,而NjCno?overlap,并且NjCoverlap,則節點vi是邊緣節點.

邊緣節點可以是社區的內部節點也可以是社區的重疊節點.每個節點vi都記錄它到它歸屬社區的核心節點的最短距離NCDi.

2.6 子群合并

在子群社區劃分中,拓撲勢值為局部最大值的節點視為山峰節點,一個山峰節點對應一個社區.但子群社區劃分中存在特殊兩種情況.1)當社交網絡數據集節點鏈接稀疏、節點度數相似時,很容易導致劃分社區數量過多,社區包含節點過少等問題,從而影響到社區的劃分質量和現實應用.2)劃分出的社區為孤立子群社區.這種孤立的子群社區不能通過核心節點間的距離關系進行合并.下面對兩種情況給出相應解決方案.

2.6.1 子群社區劃分

由于社交網絡數據集的節點數多,如果利用深度遍歷的方法計算核心節點間的距離,計算的復雜度很高,時間耗費長,所以為了快速得到上峰節點間的距離,在子群社區劃分的同時,計算子群社區中每個節點到達其社區的上峰節點的距離,最后分析了3 種情況計算子群社區間的距離.

由于社交網絡數據集的節點數多,在子群社區劃分的同時,計算子群社區中每個節點到達其社區的山峰節點的距離,并分析了計算子群社區間的距離的3 種情況.

(1)兩個子群社區不重疊但邊緣節點相連接

兩個子群社區沒有重疊節點,但是社區間的邊緣節點互聯.該情況下,由于每個邊緣節點都存儲了到達它自身歸屬的子群社區的最短距離NCD,可以利用邊緣節點進行信息交互,得到兩個子群社區的核心節點之間的距離.但是,邊緣節點自身歸屬的子群社區的核心節點的距離不一定相同,需要選取其中最短的距離為兩個子群社區不重疊但邊緣節點相連接的距離CCD.

(2)子群社區不重疊并且邊緣節點相也不連接

子群社區的劃分是根據節點的拓撲勢值由高到低進行的,但是一旦碰到當前劃分的節點其拓普勢值為局部最低點的時候,也就是劃分到山谷節點時,就結束當前子群社區的劃分.為了計算不重疊且邊緣節點不相連的兩個子群社區的核心節點間的距離,采用邊緣節點探測方法進行計算.即利用當前子群社區的邊緣節點,根據設置的步長向子群社區外部進行跳轉.每當跳到下一個節點,首先判斷當前節點是否歸屬于其他子群社區,是,根據跳轉的步長以及初始節點和當前節點的信息計算兩個社區的距離;否,跳轉到下一個節點.在做邊緣探測的時候,探測步長值設置為當前邊緣節點到達子群社區核心節點的歐式距離的1/2.

(3)子群社區重疊

當子群社區之間有重疊節點,需根據子群社區間的重疊節點到達核心節點的距離加和,取其最短的路徑長度.

對于子群社區間的距離的計算,首先分別對上述3 種情況進行處理和計算得到社區的最短距離,然后將3 種情況的結果進行比較取其最小值,最終得到相近兩兩社區的最短距離.

2.6.2 子群社區合并

通過上述的3 種情況分析和計算,得到了相近的兩個社區之間核心節點的最短路徑.根據核心節點的距離,可以將相近的社區進行合并,但是實際上很多數據集其節點的鏈接關系很稀疏,也就是存在很多孤立的節點以及非常小的“孤立”社區,如圖4所示.

圖4是citeseer 數據集的數據節點分布,圖中顯示,左上方的節點有著緊密聯系,但下方的節點非常稀疏.節點的稀疏易導致劃分的社區數被這些稀疏分布的節點所決定,使得社區劃分范圍過小失去意義.因此在子群社區劃分后,需要將子群社區針對稀疏分布情況進行合并.所以子群社區合并分為兩種.

圖4 Citeseer 數據集的節點分布

(1)相鄰子群社區合并

相近的兩個社區之間核心節點的最短路徑存放在CCD中,計算d=max(CCD),設置φ 為合并參數取值0-1,φd為合并距離.當CCDij<φd時,將兩個社區進行合并,隨機將兩個子群社區中的一個核心節點設置為合并后社區的核心節點.

(2)稀疏子群社區合并

設定規則:核心節點的信息屬性相同的稀疏子群社區合并成為一個大社區.

3 算法實驗與結果分析

所有實驗均在Intel(R)Core(TM)i7- CPU 3300 和8.00 GB RAM 的個人計算機(PC)上使用Visual Studio 2015 上實現.

3.1 標準實驗數據集

為驗證算法有效性,以下給出3 個同時擁有鏈接和屬性的社區網絡數據集信息,見表4.

表4 數據集信息

3.2 評估標準方法

(1)改進的模塊度由于本文是對重疊社區進行社區劃分,所以對于模塊度的評估標準采用的是一種引入隸屬系數的優化基礎上同時發現重疊和層次社區結構的方法,節點的隸屬系數被重新定義為該節點歸屬社區的個數.并且改進的模塊度值越高,說明社區內部鏈接更為緊密.其具體公式如下:

其中,Oi表示的是節點i所歸屬社團的數量,其余和非重疊社團發現評價指標模塊度Q類似.

(2)信息熵Entropy.信息熵將社區內部節點用于不相同屬性的情況利用公式進行放大,由此判斷社區對于屬性劃分的合理性.信息熵值越大,說明劃分出的社區內部節點擁有不同屬性的情況越多,從屬性的角度分析社區劃分不合理,由此希望信息熵值小.信息熵的公式如下:

其中,entropy(ai,cj)=?pijlog2pij,pij為 社區j中的節點具有屬性值ai的比例.

(3)社區重疊度Overlap.社區重疊節點的個數決定了社區重疊度Overlap的值.它體現了網絡耦合度,計算公式如下:

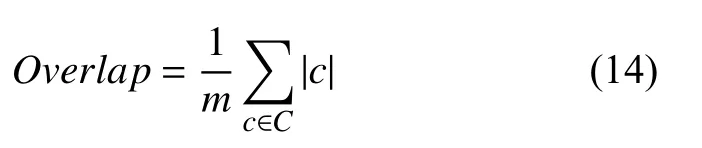
其中,|c|表示社區c的節點個數,m表示網絡節點個數.

(4)綜合指標F.一般情況下,重疊度高的網絡其模塊度相對較低,兩者呈現負相關性.而對于實驗結果而言,模塊度越大,信息熵和重疊度越小,社區挖掘的質量就越好.所以綜合以上情況,為了輸出更為合適的社區結果,定義F值為綜合評估指標:

3.3 對比實驗

3.3.1 有屬性數據集實驗對比

在有屬性數據集實驗中,將子群社區的劃分與合并進行詳細的分析.并且為了更好地展示本文提出的算法的優越性,將本文提出的算法與DOCET 算法、LANMF 算法、LPPB 算法[14]、Louvain 算法[15]、SCD算法[16]和DEMON 算法[17]進行實驗對比.DOCET 算法、Louvain 算法、SCD 算法和DEMON算法只考慮了社交網絡數據集中節點的鏈接信息,而LANMF 算法和LPPB 算法利用社交網絡數據集中節點的鏈接信息和屬性信息進行社區劃分.這3 個數據集中,DOCET算法、LANMF 算法、LPPB 算法、SCD 算法和DEMON算法都能進行重疊社區的劃分,而Louvain 算法主要針對的是非重疊節點的劃分.

(1)子群社區劃分

對3 個有屬性數據集進行子群社區的劃分.首先,根據節點拓撲勢值的局部最高點確定核心節點.再利用核心節點進行子群社區劃分.最后,將子群社區劃分結果進行計算匯總,具體如表5所示.

表5 有屬性數據集的子群社區劃分

如表5所示,在citeseer 數據集的子群社區數489 個但其中有262 個孤立的子群社區數,也就是一半的社區是孤立子群社區.而這些孤立子群社區節點的數量都小于10,由此citeseer 數據集一半的子群社區的節點數過小.cora 數據集的子群社區數是233 個,其中1/4 的子群社區是孤立子群社區.而WebKB 數據集子群社區數是35 個,它的子群社區劃分數量相對于其它兩個有屬性數據集最小但綜合指標最高.通過表中的群社區數和綜合指標的數據看,WebKB 數據集當前的子群劃分效果好,而citeseer 數據集和cora 數據集子群社區數多,孤立子群社區數占子群社區數的比例大,需要將這些數據集進行進一步的合并,確保社區劃分的綜合質量.

(2)子群社區合并

子群劃分實驗中,已經將3 個有屬性的數據集進行的子群社區的劃分,接下來根據子群社區間的距離CCD和設置的合并范圍φd進行社區的合并,φ 的取值為0.2,結果如表6所示.

如表5和表6所示,citeseer 數據集由498 個子群社區合并成為了132 個社區,是合并前子群社區數量的1/4;cora 數據集由233 個子群社區合并成為45 個社區,是合并前子群社區數量的1/5;WebKB 數據集由于數據量小,合并后一共由20 個社區,是合并前子群社區數量的4/7.所以本文提出的算法在社區合并后,3 個有屬性數據集的社區數都有所下降.而綜合指標方面,citeseer 數據集由合并前0.995442 降到0.909849,而cora 數據集也由合并前0.994164 降到0.876 022.citeseer 數據集和cora 數據集合并后綜合指標和合并前的綜合指標差距在0.1 左右.然而,造成這兩個數據集在合并后綜合指標下降的原因是合并子群社區后改進后的模塊度下降導致.citeseer 數據集的改進模塊度由合并前0.684279 降到0.612224,而重疊度和信息熵的變化不明顯.同樣的cora 數據集的改進模塊度也由合并前0.654599 降到0.563148,而重疊度和信息熵的變化也不明顯.相反,WebKB 數據集的綜合指標比合并前的綜合指標高,由合并前1.259545 升高到1.309186,差距在0.05 左右.在進行子群社區的合并過程中,綜合指標在0.1 左右浮動,但是社區數量明顯減少.

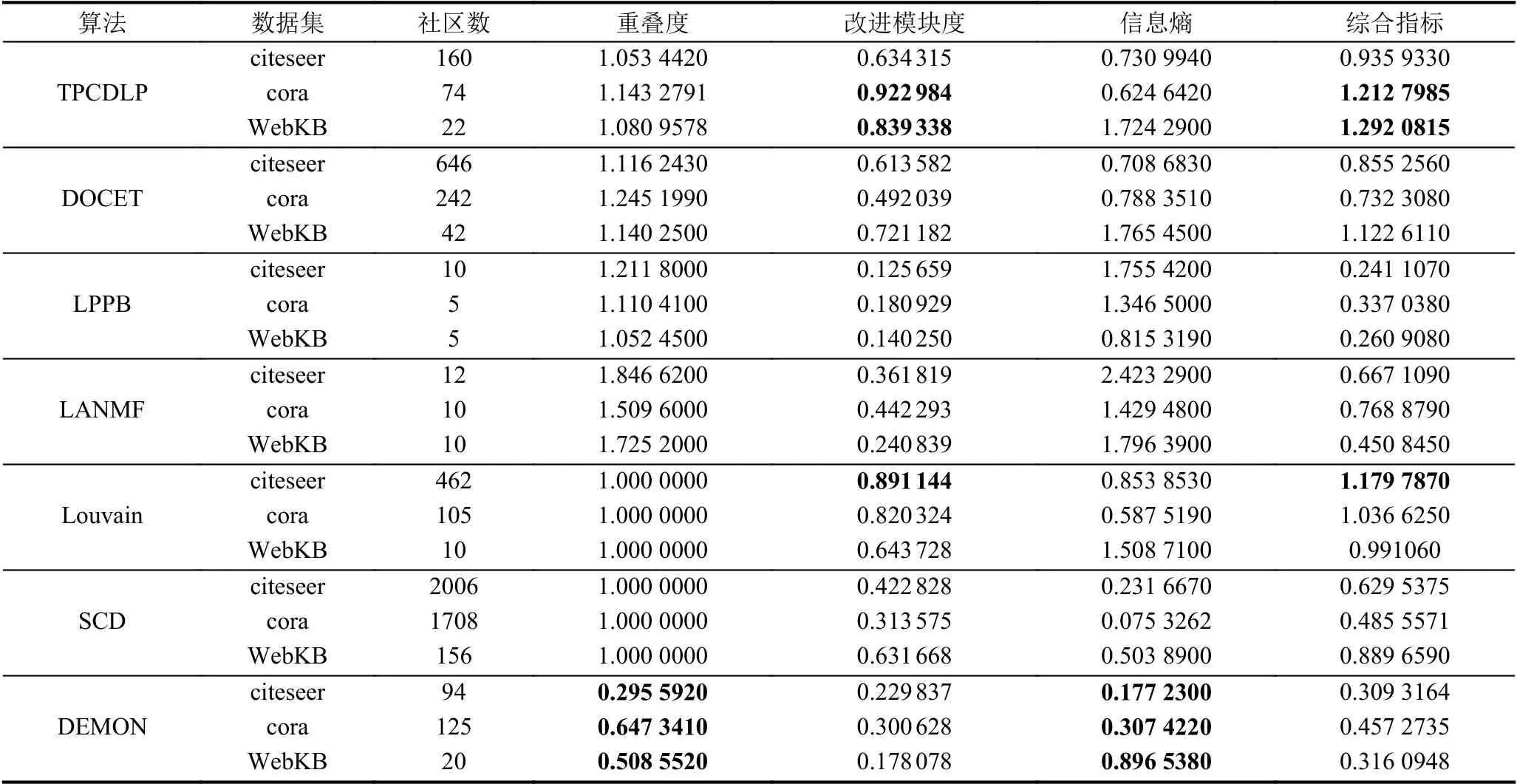
表6 子群社區合并結果

表6中,將文本提出的TPCDLP 算法和其他3 個社區檢測的算法進行了比較.通過比較可以看出,在citeseer 數據集中,Louvain 算法的綜合指標最高,再是本文提出的算法.出現這種情況的原因是由于Louvain 算法是用模塊度最優的方法進行社區的劃分.所以與其他四個算法的改進模塊度比較,Louvain算法的改進模塊度最高.雖然本文用改進的模塊度作為評估標準,但是當社區為非重疊社區時,改進的模塊度計算公式其實就是模塊度的公式.所以Louvain算法的改進模塊度相對其他算法會高,由此綜合指標也高.然而在cora 數據集和WebKB 數據集中,本文提出的算法與其他6 個社區檢測的算法比較,改進的模塊度和綜合指標都是最高.本文算法在cora 數據集上,改進的模塊度為0.922984,與其他4 個算法的改進的模塊度高出最小為0.1 左右;而綜合指標為1.212 7985,與其他6 個算法的綜合指標高出最小為0.2 左右.本文算法在WebKB 數據集上,改進的模塊度為0.839338,同樣與其他6 個算法的改進的模塊度高出最小為0.1 左右;而綜合指標為1.292 0815,同樣與其他6 個算法的綜合指標高出最小為0.2 左右.所以,通過上述分析,TPCDLP 相對其它6 個算法具有一定的優勢.

4 真實社區應用

為了驗證本文算法在現實應用中的有效性,選擇了3 個真實社交網絡數據,如表7所示.

表7 真實社交網絡數據集

Karate 為美國空手道俱樂部跆拳道俱樂部的真實劃分.

Dolphin 數據集是 D.Lusseau 等人使用長達 7年的時間觀察新西蘭 Doubtful Sound 海峽 62 只海豚群體的交流情況而得到的海豚社會關系網絡.這個網絡具有 62 個節點,159 條邊.節點表示海豚,而邊表示海豚間的頻繁接觸,該圖為無權圖.

Football 網絡,根據美國大學生足球聯賽而創建的一個復雜的社會網絡.該網絡包含 115 個節點和616 條邊,其中網絡中的結點代表足球隊,兩個結點之間的邊表示兩只球隊之間進行過一場比賽.參賽的115 支大學生代表隊被分為12 個聯盟.比賽的流程是聯盟內部的球隊先進行小組賽,然后再是聯盟之間球隊的比賽.

此處選擇了標準化互信息(NMI)評價指標來衡量算法得到的社區劃分結果與實際社區的相似性分區結果比較.NMI的計算公式如下:

其中,A和B代表社區網絡的兩個分區,C是混淆矩陣,混淆矩陣C中的元素Cij表示社區i除以A和社區j除以B的節點數.CA(CB)表示A(B)分區中的社區數,Ci(Cj)是混淆矩陣C中第i行 (j列)元素的和,N是原始社區網絡中的節點總數.當NMI值為1 時,表示A和B在社區網絡中的劃分相同.

由于3 個真實社區數據集不含屬性信息,此處采用Louvain 算法、DEMON 算法和DOCET 算法與提出的TPCDLP 算法進行比較.實驗結果如表8所示:在海豚數據集(dolphins)上,本文提出的MIFCD算法的NMI值最高;在空手道數據集(karate)上,本文提出的TPCDLP 算法的NMI 值優于DEMON 算法;在足球數據集(football)上,TPCDLP 表現好于DOCET算法.可以看出,TPCDLP 能夠基本實現真實社區劃分.

表8 歸一化互信息評價指標的實驗結果

5 總結

本文提出了一種基于標簽屬性的拓撲勢社區檢測算法.該算法利用標簽傳播方法構造節點間的鏈接權重,保證分割社區中的節點具有緊密的鏈接,并保持區域內部屬性特征高度一致.由于實際網絡數據具有冗余關系、數據存儲量大、數據分布離散等特點,采用拓撲勢最高的局部節點作為社區的核心節點進行社區劃分的算法容易導致社區重疊度高、數量多,因此,在劃分子社區之后,利用子節點與屬性特征之間的距離劃分社區,在保證社區節點之間的鏈接緊密性和屬性相關性的同時,能夠解決細粒度獨立社區問題.