基于改進的隱式廣義預測控制在燃氣發電鍋爐主汽壓中的應用

王勝 陳雨薇 徐帥 章家巖 馮旭剛

摘 要：針對燃氣發電鍋爐主汽壓控制系統存在非線性、模型參數不確定等問題，提出了一種改進的隱式廣義預測控制策略。首先，使用遺忘因子遞推最小二乘法進行模型參數辨識，建立主汽壓的離散數學模型;其次，在常規廣義預測控制理論基礎上建立主汽壓的隱式廣義預測控制系統，簡化控制算法，通過在目標函數中增加PI結構，提高系統的魯棒性。仿真結果表明，相比串級PID和常規隱式廣義預測控制，所提控制策略在模型適配時調節時間最多減少20 s，模型失配時超調量最多減少5.08%，調節時間最多降低36 s，系統魯棒性和抗干擾能力增強;工程應用表明，使用所提策略后主汽壓控制偏差在±0.2 MPa之間，控制精度顯著提高。改進的隱式廣義預測控制較好地滿足了工業生產中對主汽壓的控制要求，具有較高的研究和應用價值。

關鍵詞：系統辨識;燃氣發電鍋爐;主汽壓;遺忘因子遞推最小二乘法;隱式廣義預測控制

中圖分類號：TM621.2 ? 文獻標識碼：A ? doi：10.7535/hbkd.2020yx05003

Abstract：Aiming at the problems of non-linearity and variable model parameters of the main steam pressure control system of gas-fired power generation boiler， an improved implicit generalized predictive control strategy was proposed. First， the forgetting factor recursive least square method was used to identify the model parameters， and a discrete mathematical model of the main steam pressure was established. Second， an implicit generalized predictive control system for main steam pressure was established on the basis of conventional generalized predictive control theory， which simplified the control algorithm and improved the robustness of the system by adding a PI structure to the objective function. The simulation results show that， compared with the cascade PID and conventional implicit generalized predictive control， the proposed control strategy reduces the adjustment time by 20 s at most when the model is adapted; the overshoot decreases by up to 5.08% and the adjustment time decreases by up to 36 s when the model is mismatched， and the system robustness and anti-interference ability are improved. The engineering application shows that the main steam pressure control deviation is within ±0.2 MPa， and the control accuracy is significantly improved in the proposed strategy. The improved implicit generalized predictive control has high research and application value in the main steam pressure control in industrial production.

Keywords：system identification; gas-fired power generation boiler; main steam pressure; forgetting factor recursive least squares method; implicit generalized predictive control

中國鋼鐵企業冶金自備電廠燃氣鍋爐使用企業副產煤氣作為燃料，由于煤氣的熱值和壓力受高爐、焦爐、轉爐的生產狀況影響，導致爐膛內燃燒狀態不穩定，主汽壓波動范圍較大，不利于鍋爐的安全穩定和經濟運行[1-2]。針對冶金自備電廠燃氣發電鍋爐的主汽壓控制問題進行研究，最大限度地提高燃燒效率，對企業安全生產、節能降耗具有重要意義[3-4]。

現階段冶金自備電廠對于鍋爐主汽壓的控制主要采用常規PID方法，PID控制具有結構簡單、易于工程實施等優點[5-6]。但隨著時間的推移，鍋爐設備條件和工況不斷變化，原本整定的PID參數無法適應被控對象的變化，導致運行狀況偏離生產要求[7]。目前研究人員對于將智能控制理論引入到主汽壓控制進行了大量的理論與實踐研究。崔志強等[8]針對主汽壓系統精確模型不易確定的問題，將微分器與RBF神經網絡算法結合，設計主汽壓神經網絡控制器，在控制過程中不需要對象的模型信息，取得了一定的控制效果。程加堂等[9]將尋優者算法應用到PID參數優化中，通過計算尋優者個體適應度和最優位置，對主汽壓系統PID參數進行尋優，并與粒子群算法和遺傳算法優化的PID參數進行現場應用對比，結果表明尋優者優化算法提高了主汽壓的響應速度。李興如等[10]利用爐膛輻射能信號反映燃料量變化的快速性，作為主汽壓串級PID控制器的中間被調量，利用螢火蟲算法對PID參數尋優，系統穩定性得到了一定的提高。

上述研究表明，主汽壓系統存在大時滯和模型不確定的特點，目前主要采用智能控制算法整定PID參數[11]或建立主汽壓控制系統數學模型，但大部分只停留在理論研究階段，工程上應用不多，主要是因為實際工業現場環境復雜、工況多變，上述方法常會因為參數的不確定性而達不到滿意的控制效果。本文利用隱式廣義預測控制（IGPC）不需要反復求解Diophantine方程、能減少計算時間的優點，將PI型的反饋結構引入到IGPC的目標函數中以提高系統的魯棒性，并通過仿真和工程應用進行驗證。

1 主汽壓控制模型構建

1.1 主汽壓控制原理分析

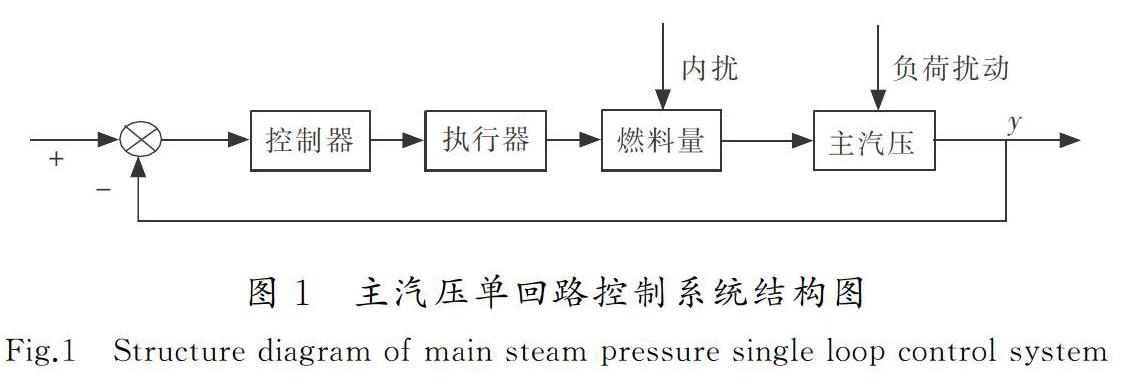
主汽壓控制系統主要分為單回路控制系統或串級回路控制系統[12]。單回路控制系統具有設計簡潔、控制參數整定方便的優點，可以克服燃料量或燃料熱值變化造成的內擾和負荷變化造成的外擾，但系統響應速度較慢，其結構如圖1所示。

當系統受到內擾或者負荷擾動時，主汽壓偏離設定值，控制器通過執行器調節煤氣量，改變燃燒狀態，使主汽壓恢復穩定。為提高鍋爐主汽壓控制系統的響應速度和穩定性，在實際中通常采用串級回路控制方案，如圖2所示。

主汽壓串級控制的副回路采用燃料量控制器，用于克服由煤氣量或煤氣熱值變化造成的內部擾動，主回路采用主汽壓控制器，用于克服由發電機組負荷變化造成的外部擾動[13-14]。當系統受到內擾時，爐膛內燃料燃燒釋放的熱量發生變化，副回路將檢測裝置得到的熱量信號傳遞給燃料量控制器，控制煤氣閥門開度，調節進入鍋爐的燃料量，改變爐膛燃燒狀況，從而實現主汽壓穩定。當系統受到外擾時，主汽壓產生變化，檢測裝置將主汽壓信號傳遞給主汽壓控制器，主汽壓控制器通過副回路調節鍋爐的燃料供應量使主汽壓恢復穩定。

1.2 主汽壓模型辨識

3 仿真分析

為驗證PI型IGPC控制策略的有效性，根據所建立的燃氣發電鍋爐主汽壓的CARIMA模型進行仿真研究，模型表達式為y（k）-1.892y（k-1）+0.903y（k-2）=-0.51u（k-1）+ξ（k）。 （12） ?根據文獻[21]的參數整定方法，經過多次仿真實驗驗證，預測控制參數取n=8，m=5，λ=0.85;比例因子和積分因子根據經驗試湊法分別取0.5和0.4，控制量增量的約束為-0.2≤ΔU≤0.2，控制輸入的約束為0≤u（k）≤1，主汽壓設定值yr=5.9 MPa。

在主汽壓模型參數適配時，采用式（12）作為主汽壓模型，對PI型IGPC與串級PID、常規IGPC控制進行仿真對比，在t=400 s和t=600 s時向系統加入幅值為1.2的脈沖干擾信號以測試系統的抗干擾性能，仿真波形如圖5所示。

由圖5可知，當主汽壓控制系統模型適配時，PI型IGPC、串級PID和常規IGPC的輸出波形均無超調，3種控制策略下的調節時間分別為290，300和310 s。當施加擾動后，常規IGPC控制輸出波形出現一定超調，且超調時間較長;串級PID超調較小，能快速恢復;PI型IGPC施加擾動后基本無超調，一直保持在穩定狀態。對比可知，PI型IGPC抗干擾性能更好，響應速度更快。

由圖6可知，當主汽壓控制系統模型參數失配時，常規IGPC控制輸出波形出現超調，超調量為5.08%，調節時間為330 s，施加擾動后超調量較大，恢復時間較長;串級PID基本無超調，但達到設定值的時間變長，為310 s，施加擾動后，超調量大，為5.78%，恢復時間較常規IGPC控制明顯縮短;PI型IGPC輸出波形達到設定值的調節時間為294 s，基本無超調，在施加擾動后僅出現少量波動，基本保持在平穩狀態。對比可知，PI型IGPC在模型失配時魯棒性更強。

4 工程應用

本文設計的優化控制系統由操作員站和現場控制器兩部分組成，指導思想是：保持鍋爐原有DCS控制系統、各種檢測儀表和控制裝置硬件條件不變，在JX-300XP DCS中加入控制權切換的功能程序，系統架構如圖7所示。優化控制系統與原DCS控制系統通過工業以太網進行連接，交換機的作用是將DCS中通過檢測裝置采集到的各參數數據傳輸給優化控制系統，使其能對鍋爐燃燒狀況進行監測，并對運行狀態進行控制。

將優化系統在冶金自備電廠150 t燃氣發電鍋爐進行運行控制。主汽壓設定值為5.9 MPa。采集系統投運前和投運后的主汽壓實時曲線，采集時間均為8 h，主汽壓曲線如圖8、圖9所示。

由圖8可知，優化系統投運前，主汽壓實時曲線波動劇烈，主汽壓值在4.2～6.3 MPa，上下波動幅值達到2.1 MPa;圖9為采用優化控制系統后的主汽壓實時曲線，主汽壓值在5.7～6.1 MPa之間波動，基本穩定在設定值5.9 MPa左右，滿足控制精度±0.2 MPa的要求。與工業現場原先的PID加手動調節方法相比，采用優化控制系統后，主汽壓能較好地穩定在設定值附近，波動范圍小，系統控制精度顯著提高。

5 結 語

針對GPC在滾動優化環節計算量大、影響時效性的問題，引入IGPC，并對算法進行改進，設計PI型IGPC主汽壓控制策略。仿真結果表明，在模型適配和模型失配時，該控制策略比串級PID和常規IGPC控制方法調節時間更短，超調量更小，系統抗干擾和魯棒性更強。工程運行結果表明，相比原有的PID控制系統，優化后的系統對主汽壓的控制精度明顯提高，較好地滿足了工業生產對主汽壓的控制要求。

目前該系統只考慮了煤氣流量對主汽壓控制的影響，對于其他因素（諸如煤氣品質、主蒸汽流量、助燃空氣流量等）的影響還需做進一步的研究。

參考文獻/References：

[1] WEI M L， ZHAO X L， FU L， et al. Performance study and application of new coal-fired boiler flue gas heat recovery system[J]. Applied Energy， 2017， 188： 121-129.

YUAN Cenjie， JIANG Wei， DONG Hongping， et al. Analysis and optimization of main steam pressure control strategy for supercritical unit DEH system in Shanghai steam turbine factory [J]. Power & Energy， 2018， 39（3）：409-412.

[13] 何國安， 張學延， 張衛軍. 汽輪發電機組軸系振動研究進展及趨勢[J]. 熱力發電， 2016， 45（11）：1-4.

HE Guoan， ZHANG Xueyan， ZHANG Weijun. Research status and development trends of turbo-generator shaft system vibration[J]. Thermal Power Generation， 2016， 45（11）：1-4.

[14] 鄭中原，趙鵬，姜玲，等.基于云平臺的發電機組節能減排實時監控系統[J].電力系統保護與控制，2019，47（7）：148-154.

ZHENG Zhongyuan，ZHAO Peng，JIANG Ling，et al.A real-time monitoring and control system for energy saving and emission reduction of generator set based on cloud platform[J].Power System Protection and Control，2019，47（7）：148-154.

[15] 鮑海靜，張韜， 張靜. 基于遺忘因子遞推最小二乘法的伺服系統轉動慣量辨識方法[J]. 上海電氣技術， 2017， 10（3）：5-9.

BAO Haijing， ZHANG Tao， ZHANG Jing. Servo system rotational inertia identification method based on forgetting factor recursive least square method[J]. Journal of Shanghai Electric Technology， 2017， 10（3）：5-9.

[16] IKEDA Y. Building dynamic property change under an earthquake evaluated by the forgetting factor recursive least squares method[J]. AIJ Journal of Technology & Design， 2012， 18（38）：51-54.

[17] 薛陽，高麗.關于丟番圖方程（20n）x+（99n）y=（101n）z[J].延安大學學報（自然科學版），2016，35（3）：16-19.

XUE Yang，GAO Li.On the Diophantine equation （20n）x+（99n）y=（101n）z[J].Journal of Yan'an University（Natural Science Edition），2016，35（3）：16-19.

[18] DENG M J. A note on the Diophantine equation [J]. Bulletin of the Australian Mathematical Society， 2014， 89（2）： 316-321.

[19] 蔡惠京.關于線性丟番圖方程的Frobenius問題[J].數學理論與應用，2019，39（2）：1-19.

CAI Huijing. On the Frobenius problem of the linear Diophantine equation[J]. Mathematical Theory and Applications， 2019，39（2）：1-19.

[20] 門洪，李項楠，史冬琳.P-隱式廣義預測控制在球磨機制粉系統中的應用[J].化工自動化及儀表，2013，40（6）：734-737.

MEN Hong， LI Xiangnan， SHI Donglin. Proportional implicit GPC control in ball pulverizing system[J]. Control and Instruments in Chemical Industry， 2013，40（6）：734-737.

[21] 陳增強，吳瑕，孫明瑋， 等.時滯系統的自抗擾廣義預測控制的性能分析[J].中南大學學報（自然科學版），2018，49（8）：1960-1970.

CHEN Zengqiang， WU Xia， SUN Mingwei， et al. Performance analysis of active disturbance rejection generalized predictive control for time-delay systems[J]. Journal of Central South University（Science and Technology），2018，49（8）：1960-1970.